下载文档原格式
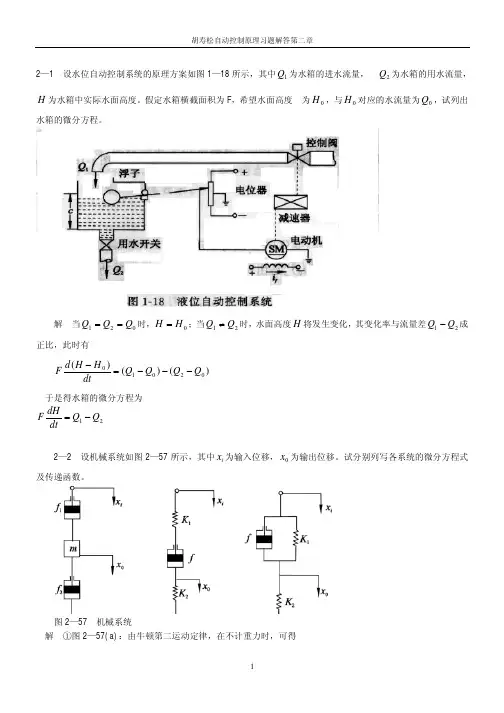
第二章 习题解答2-1试求下列各函数的拉氏变换。
（a ）()12f t t =+，（b ）2()37()f t t t t δ=+++，（c ）23()2ttt f t e ete ---=++，（d ）2()(1)f t t =+，（e ）()sin 22cos 2sin 2tf t t t e t -=++，（f ）()2cos tf t te t t -=+，（g ）()sin32cos f t t t t t =-，（h ）()1()2cos 2f t t t t =+ 解：（a ）212()F s s s =+（b ）23372()1F s s s s=+++（c ）2121()12(3)F s s s s =+++++ （d ）2()21f t t t =++，3221()F s s s s=++（e ）222222()44(1)4s F s s s s =++++++ （f ）2222211621()11(1)s d s s F s s ds s s ⎛⎫ ⎪++⎝⎭=+=++++ （g ）2222222223262231()(3)(1)s d d s s s s F s ds ds s s ⎛⎫⎛⎫ ⎪ ⎪+++⎝⎭⎝⎭=-+=-++（h ）2222211684()(4)s d s s F s s ds s s ⎛⎫ ⎪++⎝⎭=+=++2-2试求图2.54所示各信号的拉氏变换。
（a ） （b ） （c ） （d ）图2.54 习题2-2图解：（a ）021()t s e X s s s -=+（b ）000221()t s t se e X s t s s s--=-+- （c ）33112212()()t s t st s t s t s t s t s t s a ae be be ce ce a b a c b ce X s e e s s s s s s s s s s----------=-+-+-=++-（d ）11()1()1()1()()1()1()11()1()(2)1(2)1(2)1111()21()2()1()(2)1(2)1(2)x t t t T t t t T t T t T T Tt T t T t T t T t T T Tt t T t t T t T t T t T t T T T T=--+--------+--+-=-⨯-+---+--+-所以22222222211111111()222Ts Ts TsTsTs Ts s s s e e e e T T T X s e e s s T s T s T s s s s s------+++=-+-++=-+2-3运用部分分式展开，求下列各像函数的原函数。
自动控制原理习题及其解答第一章（略） 第二章例2-1 弹簧，阻尼器串并联系统如图2-1示，系统为无质量模型，试建立系统的运动方程。
解：(1) 设输入为y r ，输出为y 0。
弹簧与阻尼器并联平行移动。
(2) 列写原始方程式，由于无质量按受力平衡方程，各处任何时刻，均满足∑=0F ，则对于A 点有021=-+K K f F F F其中，F f 为阻尼摩擦力，F K 1，F K 2为弹性恢复力。
(3) 写中间变量关系式220110)()(y K F Y Y K F dty y d f F K r K r f =-=-⋅=(4) 消中间变量得 020110y K y K y K dtdy f dt dy f r r=-+- (5) 化标准形 r r Ky dtdyT y dt dy T +=+00 其中:215K K T +=为时间常数，单位[秒]。
211K K K K +=为传递函数，无量纲。
例2-2 已知单摆系统的运动如图2-2示。
(1) 写出运动方程式 (2) 求取线性化方程 解：（1）设输入外作用力为零，输出为摆角θ ，摆球质量为m 。
（2）由牛顿定律写原始方程。
h mg dtd l m --=θθsin )(22其中，l 为摆长，l θ 为运动弧长，h 为空气阻力。
（3）写中间变量关系式)(dtd lh θα= 式中，α为空气阻力系数dtd l θ为运动线速度。
（4）消中间变量得运动方程式0s i n 22=++θθθmg dt d al dtd ml （2-1) 此方程为二阶非线性齐次方程。
（5）线性化由前可知，在θ ＝0的附近，非线性函数sin θ ≈θ ，故代入式（2-1）可得线性化方程为022=++θθθmg dt d al dtd ml 例2-3 已知机械旋转系统如图2-3所示，试列出系统运动方程。
解：（1）设输入量作用力矩M f ，输出为旋转角速度ω 。
（2）列写运动方程式f M f dtd J+-=ωω式中， f ω为阻尼力矩，其大小与转速成正比。
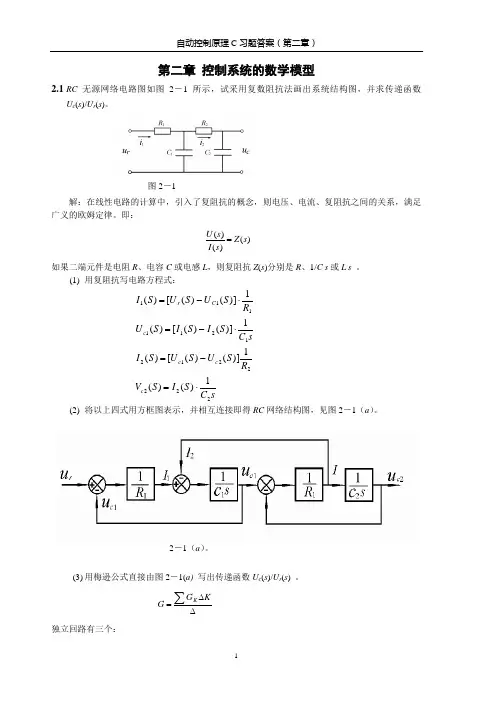
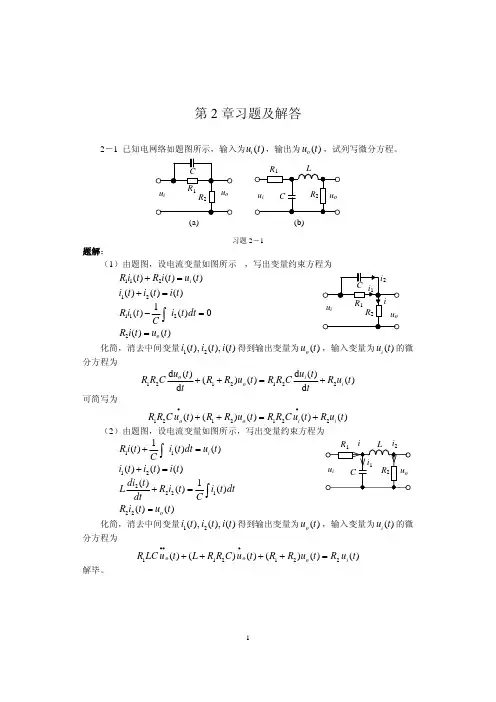
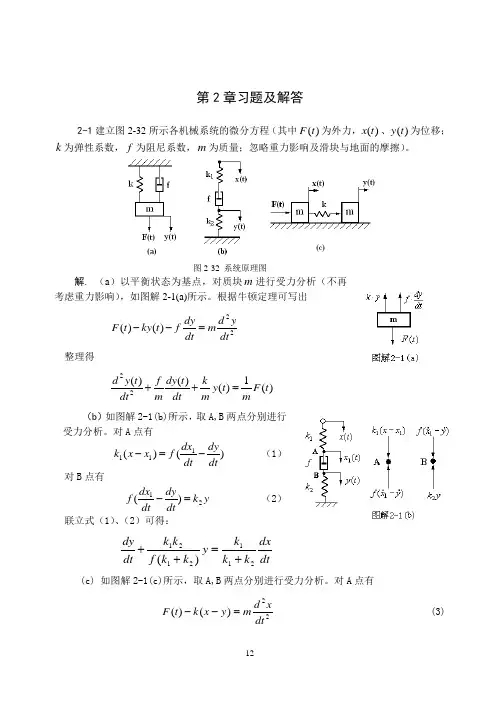
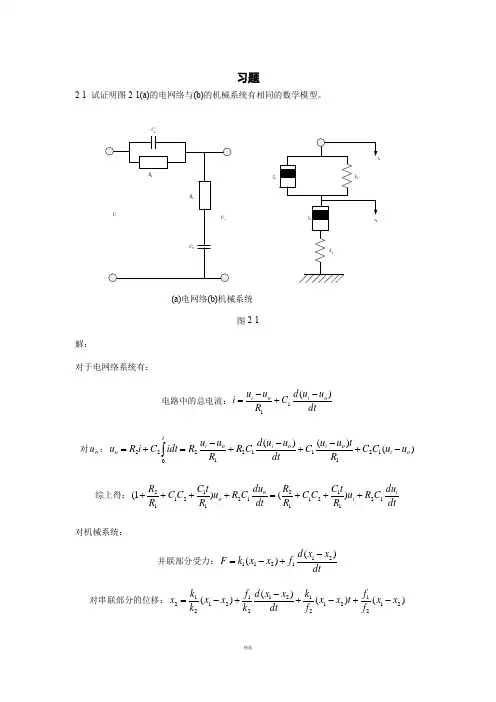
习题2-1 试证明图2-1(a)的电网络与(b)的机械系统有相同的数学模型。
1C 1f 1(a)电网络(b)机械系统图2-1解：对于电网络系统有：电路中的总电流：dtu u d C R u u i o i o i )(11-+-=对o u ：)()()(1211121222o i o i o i o i to u u C C R t u u C dt u u d C R R u u R idt C i R u -+-+-+-=+=⎰综上得：dtdu C R u R tC C C R R dt du C R u R t C C C R R i i o o 1211211212112112)()1(+++=++++对机械系统：并联部分受力：dtx x d f x x k F )()(211211-+-= 对串联部分的位移：)()()()(21212121212121212x x f f t x x f k dt x x d k f x x k k x -+-+-+-=整理得：dtdx k f x f f t f k k k dt dx k f x f f t f k k k 12122121212211212121)()1(+++=++++所以，两系统具有相同的数学模型2-5求图2-2中RC 电路和运算放大器的传递函数c ()/()i U s U s 。
1R1R(a) RC 电路 (b) RC 电路1R(c) RC 电路 (d) 运算放大器图2-2解：21212)()()R sCR R R R s u s u a r c ++=οο1)()()()()()()3122112322121121211231212112++++++++=S R C R C R C S R R C C R R C C SR C R C S R R C C R R C C s u s u b rc οο2121212)()()()R R S CR CR R R CS R s u s u c r c +++=οο21212112)()()()S LCR R R S CR R LR R LS s u s u d r c ++++=οο2-6求图2-3所示系统的传递函数C(s)/D(s)和E(s)/D(s)。
习 题 22-1 试证明图2-77(a)所示电气网络与图2 77(b)所示的机械系统具有相同的微分方程。
图2-77习题2-1图证明：首先看题2-1图中(a)()()()s U s U s U C R R -=()()()()s U Cs R s CsU s U R s I R R RR ⎪⎭⎫⎝⎛+=+=11 ()()s I s C R s U C ⎪⎪⎭⎫⎝⎛+=221()()()[]s U s U s C R s C R s U C R C -⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=112211 ()()s U s C R s C R s U s C R s C R R C ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+1122112211111 ()()()()()()s U R s C R s C s C R s U R s C R s C s C R R C11122211122211111+⨯+=⎥⎦⎤⎢⎣⎡++⨯+2-2试分别写出图2-78中各有源网络的微分方程。
图2-78 习题2-2图解： (a)()()()t u R t u R dt t du Co r r 211-=+ (b)()()()⎥⎦⎤⎢⎣⎡+-=t u R dt t du C t u R r o 2o 111(c) ()()()⎥⎦⎤⎢⎣⎡+-=tudttduCRtuR r cc2112-3某弹簧的力一位移特性曲线如图2-79所示。
在仅存在小扰动的情况下，当工作点分别为x0=-1.2，0，2.5时，试求弹簧在工作点附近的弹性系数。
解：由题中强调“仅存在小扰动”可知，这是一道非线性曲线线性化处理的问题。
于是有，在x0=-1.2，0，2.5这三个点处对弹簧特性曲线做切线，切线的导数或斜率分别为：1）()()35.5625.2805.175.040402.1==----=-=xdxdf2）20240=--==xdxdf3）65.2155.0320355.2==--==xdxdf2- 4图2-80是一个转速控制系统，其中电压u为输入量，负载转速ω为输出量。
试写出该系统输入输出间的微分方程和传递函数。
解：根据系统传动机构图可列动态如下：()()()tuKdttdiLtRire=++ω(1)iKTTem=(2)dtdJTiKTTLTLemω=-=-(3)将方程(3)整理后得：dtdKJTKiTLTω+=1(4)将方程(4)代入方程(1)后得：()tuKdtdKLJdtdTKLdtdKRJTKRreTLTTLT=++++ωωω22(5)将方程(5)整理后得：()dtdT K L T K R t u K dt d K RJ dt d K LJ LT LT r e T T --=++ωωω22 (6) 2-5 系统的微分方程组如下式中，r ，K-，K2，K 。
，Kn ，Kj ，T 均为常数。
试建立系统r(f)对c(f)的结构图，并求系统传递函数 C(s)／R(s)。
解：首先画系统结构图，根据动态方程有：然后，根据梅逊公式得：()()()()()()()()()()()()()()11111111111543314321432543343214321++++++++++++=++++++++=Ts s K K K Ts s Ts K Ts s K s K K K Ts s Ts s Ts s K s K K K Ts s K K K s K Ts K s K K K s Ts K s K K K s s R s C ττττ()()()()()543343213432214321K K K K K K K K s T K K K K Ts K s K K K s R s C +++++++=ττ 2 6 图2-8l 是一个模拟调节器的电路示意图。
X 1(s)X 2(s)X 2(s)X 3(s)X 4(s)X 5(s)C (s)τs+K 1K 2K 3/sK 4/(Ts+1)K 5① 写出输入u i ，与输出u o 之间的微分方程； ② 建立该调节器的结构图； ③ 求传递函数U o (s)／U r (s)。
解：根据电路分析需要，引入中间变量v o1(t )，v o2(t )，然后，由电路图可知：()()()s U s C R R s U R s U i o1121o 11⎪⎪⎭⎫ ⎝⎛+-=+ （1） ()()s sU C R s U o223o1-= （2） ()()s U R R s U o245o -= （3） 采用代入法，将上述3个方程联立求解得：()()()[]()()()[]s U s U s C R s C R R R R R s U s U R s C R R s C R R R s U o i 12243152o i 11222345o 1111++-=++⨯⨯-= ()()()s U sC R R s C R s C R R R R R s U i 15212243152o 1++-=()()()⎪⎪⎭⎫⎝⎛++⨯=++-=12243115224311243151522431212243152i o 1C R C R R R C R R C R R R s s C C R R R R s C R R s C R R R s C R C R R R R R s U s U 2-7某机械系统如图2-82所示。
质量为m 、半径为R 的均质圆筒与弹簧和阻尼器相连(通过轴心)，假定圆筒在倾角为α的斜面上滚动(无滑动)，求出其运动方程。
解：首先，对圆辊进行受力分析；根据分析结果可知：-K x 1mg sin α-Bd x /dtmgmg cos αN21211sin dt x d m dt dx B Kx mg =--ααsin 11212mg Kx dtdxB dt x d m =++ 2 8 图2-83是一种地震仪的原理图。
地震仪的壳体固定在地基上，重锤M 由弹簧K 支撑。
当地基上下震动时，壳体随之震动，但是由于惯性作用，重锤的运动幅度很小，这样它与壳体之间的相对运动幅度就近似等于地震的幅度，而由指针指示出来。
活塞B 提供的阻尼力正比于运动的速度，以便地震停止后指针能及时停止震动。
①写出以指针位移y 为输出量的微分方程； ②核对方程的量纲。
解：首先，对重锤进行受力分析；根据分析结果可知：22dt yd m dt dy B Ky mg =--mg Kx dt dxB dtx d m =++112122 9 试简化图2-84中各系统结构图，并求传递函数c(s)／R(s)。
图2-84习题2-9图解：(a)，根据梅逊公式得：前向通道传递函数P k ：()()s G s G P 211=；()()s G s G P 232=回路通道传递函数L i ：()()()s H s G s G L 2211-=；()()s H s G L 122-=特征方程△：()()()()()s H s G s H s G s G L i 1222111++=∑-=∆由于回路传递函数都与前向通路相“接触”，所以。
余子式：121=∆=∆ 系统传递函数为：()()()()()()()()()()()()s H s G s H s G s G s G s G s G s G s R s C s 1222132211+++==Φ (b)，根据梅逊公式得：前向通道传递函数P k ：()()s G s G P 211=；回路通道传递函数L i ：()()s H s G L 111-=；()()s H s H L 212-= 特征方程△：()()()()s H s H s H s G L i 211111++=∑-=∆由于回路传递函数L 2与前向通路相“不接触”，所以。
余子式：()()s H s H 2111+=∆ 系统传递函数为：()()()()()()()()()()()()s G s H s H s H s G s H s H s G s R s C s 2211121111+++==Φ(c)，根据梅逊公式得：前向通道传递函数P k ：()()()()s G s G s G s G P 43211=； 回路通道传递函数L i ：()()()()()s H s G s G s G s G L 143211=；()()()()s H s G s G s G L 23212-= ()()()s H s G s G L 3323-= ()()()s H s G s G L 4434-=特征方程△：()()()()()()()()()()()()()()()s H s G s G s H s G s G s H s G s G s G s H s G s G s G s G L i 44333223211432111+++-=∑-=∆由于回路传递函数都与前向通路相“接触”，所以。
余子式：11=∆系统传递函数为：()()()()()()()()()()()()()()()()()()()()()()s H s G s G s H s G s G s H s G s G s G s H s G s G s G s G s G s G s G s G s R s C s 44333223211432143211+++-==Φ2-10试用梅逊公式求解习题2-9所示系统的传递函数C(s)／R(s)。
2-11 系统的结构如图2-85所示。
① 求传递函数C 1(s)/R I (s)，C 1(s)/R 2(s)，C 2(s)/R I (s)，C 2(s) R 2(s)，② 求传递函数阵G (s)C (s)= G (s)R (s)，其中()()()⎥⎦⎤⎢⎣⎡=s G s G s 21G ，()()()⎥⎦⎤⎢⎣⎡=s R s R s 21R 。
解：C 1(s)/R I (s)，根据梅逊公式得：前向通道传递函数P k ：()()()s G s G s G P 3211=；()()()()()s G s G s G s G s G P 385712=；回路通道传递函数∑L i ：()()s G s G L 331-=；()()()s G s G s G L 8572= ()()s H s G L 253-=相互“不接触”回路∑L i L j ：()()()()()s G s G s G s G s G L L 8573321-= ()()()()s H s G s G s G L L 253331=特征方程△：ji i L L L ∑+∑-=∆1()()()()()()()()()()()()()()()()s H s G s G s G s G s G s G s G s G s H s G s G s G s G s G s G 25338573325857331--++-+=由于回路传递函数都与前向通路相“接触”，所以。
