单筋矩形截面正截面承载力计算示例.

单筋矩形截面正截面承载力计算方法
在计算单筋矩形截面的承载力时，我们需要考虑两种主要的受力情况：剪力和弯矩。

以下是单筋矩形截面承载力计算的详细方法。

1.剪力承载力计算：
首先，计算纵向筋的贡献：
Vr = φ × As × fy /γs
其中，Vr为纵向筋的承载力，φ为抗剪强度折减系数，一般取0.75，As为纵向筋的截面面积，fy为纵向筋的抗拉强度设计值，γs为安全系数，一般取1.15
然后，计算混凝土的贡献：
Vc = φ × b × x × fcd /γc
其中，Vc为混凝土的承载力，b为矩形截面的宽度，x为截面混凝土
受剪应力点至受拉纵筋的距离，fcd为混凝土的抗压强度设计值，γc为
混凝土安全系数，一般取1.5
最终，剪力承载力为：
V=Vr+Vc
2.弯矩承载力计算：
首先，计算纵向筋的承载力：
Mr = φ × (As × fy) × (d - a/2) / γs
其中，Mr为纵向筋的弯矩承载力，d为矩形截面的有效高度，a为纵向筋至受压边缘的距离，As为纵向筋的截面面积，fy为纵向筋的抗拉强度设计值，γs为安全系数。

3.组合效应计算：
在实际情况中，剪力和弯矩通常是同时作用于单筋矩形截面的。

根据极限状态设计原则，剪力和弯矩的组合效应需要考虑。

计算组合效应时，可以根据相应的超信度进行组合，采用相应的抗风定额规定即可。

综上所述，单筋矩形截面的承载力计算主要包括剪力承载力和弯矩承载力的计算，并根据实际受力情况考虑组合效应。

详细的计算公式和参数需要根据具体情况进行设计和选择，以确保梁的安全可靠性。

单筋矩形截面受弯构件正截面承载力计算单筋矩形截面受弯构件是指具有一个纵向钢筋（单筋）和一个矩形截面的构件。

在受弯时，矩形截面受到压力，而钢筋受到拉力，通过计算正截面承载力可以确定该构件的安全性能。

下面将介绍单筋矩形截面受弯构件正截面承载力的计算方法。

首先，计算正截面的受压区高度h和内力矩M。

假设构件受弯时的截面高度为h，宽度为b，截面厚度为d。

根据等截面原则，构件的正截面宽度和截面高度相等，即b=h。

构件的弯矩M由下式计算得出：M=Rd·Z，其中Rd为设计弯矩，Z为正截面抵抗矩。

然后，计算正截面抵抗矩Z。

在单筋矩形截面中，正截面抵抗矩由钢筋和混凝土组成。

钢筋的抵抗矩可由以下公式计算得出：Zs=As·fy·(h-d/2)，其中As为钢筋截面面积，fy为钢筋的抗拉强度。

混凝土的抵抗矩可由以下公式计算得出：Zc=0.85·fck·(b·h-(As+Asc)·(h/2-d/2))，其中fck为混凝土的抗压强度，Asc为纵向钢筋表面积。

正截面的抵抗矩由钢筋的抵抗矩和混凝土的抵抗矩之和得出：Z=Zs+Zc。

接下来，计算正截面的承载力。

正截面受弯构件的承载力由以下条件中的最不利情况决定：1.混凝土达到极限压应力或者钢筋达到屈服应力；2. 混凝土达到达到破坏应变时，即混凝土压应力达到0.45fck或者钢筋达到屈服应变。

计算混凝土达到极限压应力的情况下的承载力，可以得到下式：Nc=0.85·fcd0·A+(Rd-Zs)/Rd·fctd0·A，其中fcd0为混凝土的设计强度，fctd0为混凝土的设计抗拉强度，A为截面面积。

计算钢筋达到屈服应力的情况下的承载力，可以得到下式：Ns=(Zs/0.9zτs)·fsd，其中z为混凝土的截面中和高度，τs为混凝土的应力分布系数，fsd为钢筋的设计抗拉强度。

综合两种情况，正截面受弯构件的正截面承载力Fc为较小值：Fc=min{Nc,Ns}。

单筋矩形正截面受弯承载力计算公式根据图1和截面内力平衡条件，并满足承载能力极限状态计算表达式的要求，可得出如下基本计算公式：图1 单筋矩形截面梁板正截面受弯承载力计算简图∑x=0 f c bx=f y A s（1）∑M=0 KM≤f c bx（h0−）（2）式中M——弯矩设计值（N·mm）；f c——混凝土轴心抗压强度设计值（N/mm2），按附表1–2取用；b——矩形截面宽度（mm）；x——混凝土受压区计算高度（mm）；h0——截面有效高度（mm）；f y——受拉钢筋的强度设计值（N/mm2），按附表1–5取用；A s——受拉钢筋的截面面积（mm2）；K——承载力安全系数, 按表1–7取用。

利用基本公式进行截面计算时，必须求解方程组，比较麻烦。

为简化计算，将式（1）、(2）改写如下：将ξ=x/h0代入公式（1）、(2)，并引入截面抵抗矩系数αs，令αs =ξ（1–ξ）（3）则基本公式改写为：f c bξh0=f y A s（4）KM≤αs f c bh02（5）由式（4）可得：ρ= ξf c/f y基本公式是根据适筋破坏的情况推导出来的。

因此，它的适用条件为：（1）ρ≤ρmax或x ≤ξb h0或ξ≤ξb，以防止发生超筋破坏，ρmax=ξb f c/f y；基本公式是依据适筋构件破坏时的应力图形情况推导的，当受拉钢筋屈服的同时，受压区混凝土也达到极限压应变εcu，梁发生的临界破坏状态，就是适筋梁与超筋梁的界限。

但为了结构的安全，更有效地防止发生超筋破坏,，应用基本公式和由它派生出来的公式计算时，必须符合此条件。

（2）ρ≥ρmin，以防止发生少筋破坏钢筋混凝土梁板构件破坏时承担的弯矩等于同截面素混凝土梁板构件所能承担的弯矩时的受力状态，为适筋破坏与少筋破坏的分界。

这时梁板的配筋率应是适筋梁板的最小配筋率。

《规范》不仅考虑了这种“等承载力”原则，而且还考虑了混凝土的性质和工程经验等。

因此，基本公式应符合此条件。

4.3.2 单筋矩形截面承载能力计算矩形截面通常分为单筋矩形截面和双筋矩截面两种形式。

只在截面的受拉区配有纵向受力钢筋的矩形截面，称为单筋矩形截面（图4-10）。

不但在截面的受拉区，而且在截面的受压区同时配有纵向受力钢筋的矩形截面，称为双筋矩形截面。

需要说明的是，为了构造上的原因（例如为了形成钢筋骨架），受压区通常也需要配置纵向钢筋。

这种纵向钢筋称为架立钢筋。

架立钢筋与受力钢筋的区别是：架立钢筋是根据构造要求设置，通常直径较细、根数较少；而受力钢筋则是根据受力要求按计算设置，通常直径较粗、根数较多。

受压区配有架立钢筋的截面，不是双筋截面。

图4-10 单筋矩形截面根据4.3.1的基本假定，单筋矩形截面的计算简图如图4-11所示。

图4-11 单筋矩形截面计算简图为了简化计算，受压区混凝土的应力图形可进一步用一个等效的矩形应力图代替。

矩形应力图的应力取为α1f c(图4-12），f c为混凝土轴心抗压强度设计值。

所谓“等效”，是指这两个图不但压应力合力的大小相等，而且合力的作用位置完全相同。

图4-12 受压区混凝土等效矩形应力图按等效矩形应力计算的受压区高度x与按平截面假定确定的受压区高度x o之间的关系为:(4-7)系数α1和β1的取值见表4-2。

系数α1和β1的取值表表4-2◆基本计算公式由于截面在破坏前的一瞬间处于静力平衡状态，所以，对于图4-12 的受力状态可建立两个平衡方程：一个是所有各力的水平轴方向上的合力为零，即(4-8)式中b——矩形截面宽度；A s——受拉区纵向受力钢筋的截面面积。

另一个是所有各力对截面上任何一点的合力矩为零，当对受拉区纵向受力钢筋的合力作用点取矩时，有：(4-9a)当对受压区混凝土压应力合力的作用点取矩时，有：(4-9b)式中M——荷载在该截面上产生的弯矩设计值；h o——截面的有效高度，按下计算h o=h-a s。

h为截面高度，a s为受拉区边缘到受拉钢筋合力作用点的距离。

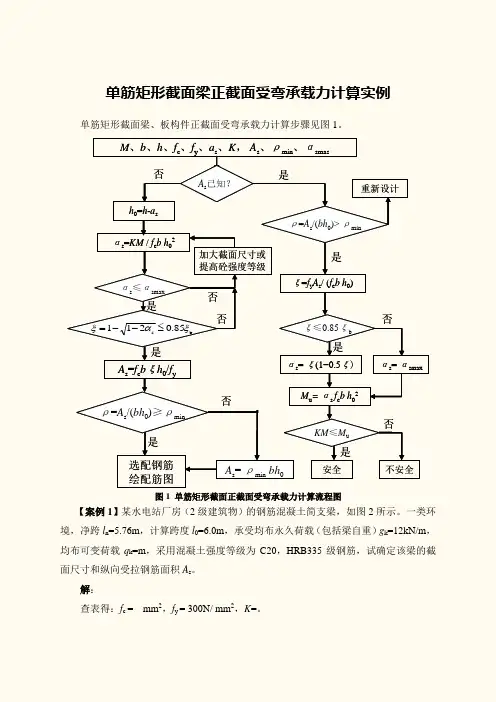
单筋矩形截面梁正截面受弯承载力计算实例单筋矩形截面梁、板构件正截面受弯承载力计算步骤见图1。

选配钢筋加大截面尺寸或是M 、b 、h 、f c 、f y 、a s 、K ，A s 、ρmin 、αsmasαs =KM / f c b h 02A s =f c b ξh 0/f ybs 85.0211ξαξ≤--=h 0=h -a s否A s = ρmin bh 0绘配筋图是是A s 已知？αs ≤αsmax提高砼强度等级ρ=A s /(bh 0)≥ρmin是ξ=f y A s / (f c b h 0)ξ≤0.85ξbαs = ξ(1−0.5ξ)M u = αs f c b h 02KM ≤M u是是安全αs = αsmax否否不安全否否否ρ=A s /(bh 0)> ρmin是重新设计图1 单筋矩形截面正截面受弯承载力计算流程图【案例1】某水电站厂房（2级建筑物）的钢筋混凝土简支梁，如图2所示。

一类环境，净跨l n =5.76m ，计算跨度l 0=6.0m ，承受均布永久荷载（包括梁自重）g k =12kN/m ，均布可变荷载q k =m ，采用混凝土强度等级为C20，HRB335级钢筋，试确定该梁的截面尺寸和纵向受拉钢筋面积A s 。

解：查表得：f c = mm 2，f y = 300N/ mm 2，K =。

（1）确定截面尺寸 由构造要求取：h =（1/8～1/12）l 0 =（1/8～1/12）×6000=750～500，取h =500mm b =（1/2～1/3）h =（1/2～1/3）×500=250～167，取b =250mm （2）内力计算M =（+ ）l 02/8=（×12+×）×62 /8 = ·m （3）配筋计算取a s =40mm ，则h 0=h –a s =500–40=460mm==2c s bh f KMα248.04602506.91076.10420.126=⨯⨯⨯⨯ 290.0248.0211211s =⨯--=--=αξ＜ξb =×=A s =f c bξh 0/f y =×250××460/300=1067mm 2 ρ= 1067/（250×460）=﹪＞ρmin =﹪（4）选配钢筋，绘制配筋图选受拉纵筋为322（A s =1140 mm 2），需要最小梁宽b min =2c +3d +2e =2×30+ 3×22+2×25=176（mm ）＜250mm ，符合构造要求。

受弯构件正截面承载力计算与截面设计系列总结之单筋矩形截面相关计算1 承载力计算：截面尺寸(b 、h 、h 0）、配筋(A s ）和材料强度（f c ，f t 、f y )等条件已知情况下，求M u ，其计算步骤如下：1.1 计算配筋率：s A bh ρ=或s 0A bh ρ= 1.2若min ρρ<，则2u crA 0.292(1 2.5)t M M f bh α==+，其中s A E 2A bh αα= ；s E cE E α= 1.3若min max ρρρ<≤，按适筋梁进行计算，由1c y s f bx f A α=求x ，再将x 代入u 1c 0y s 0()()22x x M f bx h f A h α=−=−，其中1c max b y f f αρξ=；t min max y (0.2%,45%)f f ρ= 1.4若max ρρ>，按超筋梁进行计算，先将s y b 0.80.8f ξσξ−=−代入1c s s f bx A ασ=求x 或ξ，再将x 或ξ及s y b 0.80.8f ξσξ−=−代入u 1c 0s s 0()()22x x M f bx h A h ασ=−=− 说明：上述式中0h 按如下取值：单排配筋时, 02d h h c =−−；双排配筋时，()0max 25,22d h h c d =−−+，其中，c 为混凝土的保护层厚度，d 为钢筋的 直径，c 为混凝土保护层厚度。

2 截面设计：截面尺寸(b 、h 、h 0）、材料强度（f c ，f t 、f y )和M 等条件已知情况下，求配筋A s ，为保证所设计的截面在给定弯矩作用下不发生破坏，应要求截面的弯矩承载力不低于其所受弯矩，即：M u ≥ M ，其计算步骤如下：2.1 按22u,max 1c 0b b s,max 1c 0(10.5)M f bh f bh αξξαα=−=，其中s,max b b (10.5)αξξ=−求u,max M ，若u,max M M >则需加大截面重新计算；若u,max M M ≤则进行下一步2.2 由u 1c 0y s 0()()22x x M f bx h f A h α=−=−和1c y s f bx f A α=求s A2.3 计算配筋率：s A bhρ= 2.4 若min ρρ≥，计算结束2.5 若min ρρ<，取s min A bh ρ=说明：设计时钢筋直径未知，故上述式中0h 按如下取值：对钢筋混凝土梁，单排配筋时, 035h h =−（mm ）；双排配筋时，060h h =−（mm ），对钢筋混凝土板，020h h =−（mm ）。

3.2 正截面承载力计算钢筋混凝土受弯构件通常承受弯矩和剪力共同作用，其破坏有两种可能：一种是由弯矩引起的，破坏截面与构件的纵轴线垂直，称为沿正截面破坏；另一种是由弯矩和剪力共同作用引起的，破坏截面是倾斜的，称为沿斜截面破坏。

所以，设计受弯构件时，需进行正截面承载力和斜截面承载力计算。

一、单筋矩形截面1.单筋截面受弯构件沿正截面的破坏特征钢筋混凝土受弯构件正截面的破坏形式与钢筋和混凝土的强度以及纵向受拉钢筋配筋率ρ有关。

ρ用纵向受拉钢筋的截面面积与正截面的有效面积的比值来表示，即ρ＝As/(bh0)，其中A s为受拉钢筋截面面积；b为梁的截面宽度；h0为梁的截面有效高度。

根据梁纵向钢筋配筋率的不同，钢筋混凝土梁可分为适筋梁、超筋梁和少筋梁三种类型，不同类型梁的具有不同破坏特征。

①适筋梁配置适量纵向受力钢筋的梁称为适筋梁。

适筋梁从开始加载到完全破坏，其应力变化经历了三个阶段，如图3.2.1。

第I阶段（弹性工作阶段）：荷载很小时，混凝土的压应力及拉应力都很小，应力和应变几乎成直线关系，如图3.2.1a。

当弯矩增大时，受拉区混凝土表现出明显的塑性特征，应力和应变不再呈直线关系，应力分布呈曲线。

当受拉边缘纤维的应变达到混凝土的极限拉应变εtu时，截面处于将裂未裂的极限状态，即第Ⅰ阶段末，用Ⅰa表示，此时截面所能承担的弯矩称抗裂弯矩M cr，如图3.2.1b。

Ⅰa阶段的应力状态是抗裂验算的依据。

第Ⅱ阶段（带裂缝工作阶段）：当弯矩继续增加时，受拉区混凝土的拉应变超过其极限拉应变εtu，受拉区出现裂缝，截面即进入第Ⅱ阶段。

裂缝出现后，在裂缝截面处，受拉区混凝土大部分退出工作，拉力几乎全部由受拉钢筋承担。

随着弯矩的不断增加，裂缝逐渐向上扩展，中和轴逐渐上移，受压区混凝土呈现出一定的塑性特征，应力图形呈曲线形，如图3.2.1c。

第Ⅱ阶段的应力状态是裂缝宽度和变形验算的依据。

当弯矩继续增加，钢筋应力达到屈服强度f y，这时截面所能承担的弯矩称为屈服弯矩M y。