定积分的计算与广义积分

七大积分总结一． 定积分1. 定积分的定义：设函数f(x)在[a,b]上有界，在区间[a,b]中任意插入n －1个分点：a=x 0<x 1<x 2<……<x i-1<x i <x i+1<……<x n-1<x n =b,把区间[a,b]分成n 个小区间：[x 0,x 1]……[x i-1,x i ]……[x n-1,x n ]，记△x i =x i －x i-1(i=1,2,3,……,n)为第i 个小区间的长度，在每个小区间上[x i-1,x i ]上任取一点ξi (x i-1≤ξi ≤i )，作乘积:f(ξi )△x i (i=1,2,3,……,n),并作合式： i i x f ∆=∑-)(S i n1ξ记λ=max{△x 1, △x 2, △x 3……, △x n },若不论对[a,b]怎样分法，也不论在小区间[x i-1,x i ]上点ξi 怎样取法，只要当λ→0时，S 的极限I 总存在，这时我们称I 为函数f(x)在区间[a,b]上定积分（简称积分），记做： ∑⎰=→∆==ni i i ba x f I dx x f 10)()(lim ξλ其中f(x)称为被积函数，f(x)dx 称为被积表达式，x 称为积分变量，a 称为积分下限，b 称为积分上限，[a,b]称为积分区间，∑=∆ni iixf 0)(ξ称为积分和。

如果f(x)在[a,b]上的定积分存在，则称f(x)在[a,b]上可积。

关于定积分的定义，作以下几点说明：（1） 积分值仅与被积函数及积分区间有关，而与积分变量的字母记法无关，即⎰⎰⎰==bab abadu u f dt t f dx x f )()()(。

（2） 定义中区间的分法与ξi 的取法是任意的。

（3） 定义中涉及的极限过程中要求λ→0，表示对区间[a,b]无限细分的过程，随λ→0必有n →∞，反之n →∞并不能保证λ→0，定积分的实质是求某种特殊合式的极限：例：∑⎰=∞→=ni n n i f dx x f 110n 1)()(lim （此特殊合式在计算中可以作为公式使用） 2. 定积分的存在定理定理一 若函数f(x)在区间[a,b]上连续，则f(x)在[a,b]上可积。

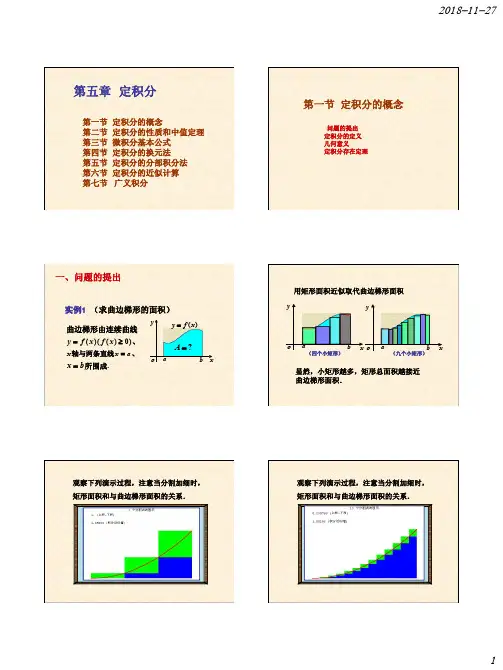
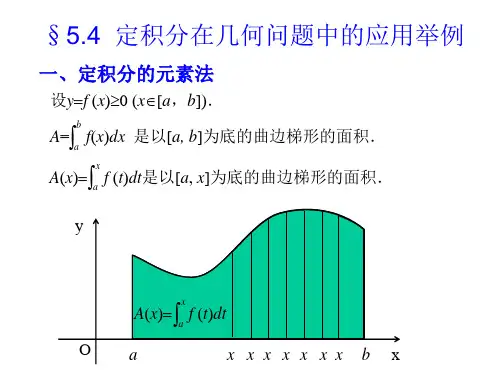
第五章 定积分第一节 定积分的概念第二节 定积分的性质和中值定理第三节 微积分基本公式第四节 定积分的换元法第五节 定积分的分部积分法第六节 定积分的近似计算第七节 广义积分问题的提出定积分的定义 几何意义定积分存在定理第一节 定积分的概念abxyo?=A 曲边梯形由连续曲线实例1 （求曲边梯形的面积）)(x f y =)0)((≥x f 、x 轴与两条直线a x =、b x =所围成.一、问题的提出)(x f y =ab xyoab x yo用矩形面积近似取代曲边梯形面积显然，小矩形越多，矩形总面积越接近曲边梯形面积．（四个小矩形）（九个小矩形）观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．曲边梯形如图所示，,],[1210b x x x x x a b a n n =<<<<<=- 个分点，内插入若干在区间a bxyoi ξi x 1x 1-i x 1-n x ;],[],[11---=∆i i i i i x x x x x n b a 长度为，个小区间分成把区间形面积，曲边梯形面积用小矩上任取一点在每个小区间i i i x x ξ-],[1ii i x f A ∆ξ≈)(:))(],[(1近似为高为底，以i i i f x x ξ-（1）分割（2）近似ini i x f A ∆≈∑=)(1ξ曲边梯形面积的近似值为ini i x f A ∆=∑=→)(lim 10ξλ时，趋近于零即小区间的最大长度当分割无限加细)0(},,max{,21→∆∆∆=λλn x x x 曲边梯形面积为（3）求和（4）取极限实例2 （求变速直线运动的路程）设某物体作直线运动，已知速度)(t v v =是时间间隔],[21T T 上t 的一个连续函数，且0)(≥t v ，求物体在这段时间内所经过的路程.思路：把整段时间分割成若干小段，每小段上速度看作不变，求出各小段的路程再相加，便得到路程的近似值，最后通过对时间的无限细分过程求得路程的精确值．（1）分割212101T t t t t t T n n =<<<<<=- 1--=∆i i i t t t ii i t v s ∆≈∆)(τ部分路程值某时刻的速度（3）求和ii ni t v s ∆≈∑=)(1τ（4）取极限},,,max{21n t t t ∆∆∆= λini i t v s ∆=∑=→)(lim 10τλ路程的精确值（2）近似设函数)(x f 在],[b a 上有界，记},,,max{21n x x x ∆∆∆= λ，如果不论对],[b a 在],[b a 中任意插入若干个分点bx xx x x a nn =<<<<<=-121把区间],[b a 分成n 个小区间，各小区间的长度依次为1--=∆i i i x x x ，),2,1( =i ，在各小区间上任取一点i ξ（i i x ∆∈ξ），作乘积i i x f ∆)(ξ ),2,1( =i 并作和i i ni x f S∆=∑=)(1ξ，二、定积分的定义定义怎样的分法，⎰==ba I dx x f )(ii ni x f ∆∑=→)(lim 10ξλ被积函数被积表达式积分变量积分区间],[b a 也不论在小区间],[1i i x x -上点i ξ怎样的取法，只要当0→λ时，和S 总趋于确定的极限I ，我们称这个极限I 为函数)(x f 在区间],[b a 上的定积分，记为积分上限积分下限积分和几点说明：（1） 定积分是一个数值，它仅与被积函数及积分区间有关，⎰b a dx x f )(⎰=b a dt t f )(⎰=ba duu f )(而与积分变量的字母无关.)( ,)()( 2⎰⎰⎰=-=aaabbadx x f dx x f dx x f 规定：）（.],[)(],[)( 3的取法无关的分法及的和式的极限与所表示上可积，则在区间若）（i bab a dx x f b a x f ξ⎰,0)(≥x f ⎰=ba Adx x f )(曲边梯形的面积,0)(≤x f ⎰-=ba Adx x f )(曲边梯形的面积的负值a b xyo)(x f y =AxyoabA -)(x f y =三、定积分的几何意义1A 2A 3A 4A 4321)(A A A A dx x f ba ⎰=-+-,],[)(变号时在区间b a x f 三、定积分的几何意义.)(是面积的代数和⎰badx x f几何意义：积取负号．轴下方的面在轴上方的面积取正号；在数和．之间的各部分面积的代直线的图形及两条轴、函数它是介于x x b x a x x f x ==,)(++--当函数)(x f 在区间],[b a 上连续时，定理1定理2 设函数)(x f 在区间],[b a 上有界，且只有有限个间断点，则)(x f 在四、定积分的存在定理区间],[b a 上可积.例1 利用定义计算定积分.12dx x ⎰解将]1,0[n 等分，分点为nix i =，(n i ,,2,1 =)小区间],[1i i x x -的长度nx i 1=∆，(n i ,,2,1 =)取i i x =ξ，(n i ,,2,1 =)i i n i x f ∆∑=)(1ξi i ni x ∆=∑=21ξ,12i ni ix x ∆=∑=.,102的选取无关及法故和式极限与区间的分可积因为i dx x ξ⎰n n i ni 121⋅⎪⎭⎫ ⎝⎛=∑=∑==n i i n 12316)12)(1(13++⋅=n n n n ,121161⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=n n ∞→⇒→n 0λdx x ⎰102i i ni x ∆=∑=→210lim ξλ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=∞→n n n 121161lim .31= 几何上是曲线y=x 2,直线x=1及x 轴围成的曲边三角形面积.例2 利用定义计算定积分.121dx x⎰解在]2,1[中插入分点 12,,,-n q q q ,典型小区间为],[1ii q q -，（n i ,,2,1 =）小区间的长度)1(11-=-=∆--q qq q x i i i i ,取1-=i i qξ，（n i ,,2,1 =）i i ni x f ∆∑=)(1ξi ni ix ∆=∑=11ξ)1(1111-=-=-∑q q q i ni i ∑=-=ni q 1)1()1(-=q n 取2=nq即nq 12=),12(1-=n n )12(lim 1-+∞→xx x x xx 112lim1-=+∞→,2ln =)12(lim 1-∴∞→nn n ,2ln =dx x ⎰211i ni ix ∆=∑=→101lim ξλ)12(lim 1-=∞→n n n .2ln =i i ni x f ∆∑=)(1ξ原式⎥⎦⎤⎢⎣⎡π+π-++π+π=∞→n n n n n n n nsin )1(sin 2sin sin 1lim π=∑=∞→n i n n i n 1sin 1lim n n i ni n π⋅⎪⎭⎫ ⎝⎛ππ=∑=∞→1sin lim 1.sin 10⎰ππ=xdx ix ∆i ξ例3：将下列和式极限表示成定积分.⎥⎦⎤⎢⎣⎡-+++∞→n n n n n n πππ)(sin sin sin lim121 ：五、小结１．定积分的实质：特殊和式的极限．２．定积分的思想和方法：分割化整为零求和积零为整取极限精确值——定积分求近似以直（不变）代曲（变）取极限Z .思考n n n n f n f n f ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim 试证.1)(ln ⎰=dxx f e 2：将和式极限，表示成定积分.⎥⎦⎤⎢⎣⎡-++-+-∞→2222241241141lim n n n n n 证明n n n n f n f n f ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫⎝⎛∞→ 21lim ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→=n n n n f n f n f e21lim ln n n n n f n f n f ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim 试证.1)(ln ⎰=dx x f e 利用对数的性质得⎪⎭⎫⎝⎛∑==∞→n i f n ni n e1ln 1lim n n i f ni n e1ln lim 1⋅⎪⎭⎫ ⎝⎛∑==∞→ 指数上可理解为：)(ln x f 在]1,0[区间上的一个积分和．分割是将]1,0[n 等分分点为nix i =，（n i ,,2,1 =）⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→=n n n n f n f n f e21ln lim 极限运算与对数运算换序得nn i f n i n 1ln lim 1⋅⎪⎭⎫ ⎝⎛∑=∞→⎰=10)(ln dx x f 故nn n n f n f n f ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim.10)(ln ⎰=dxx f e 因为)(x f 在区间]1,0[上连续，且0)(>x f 所以)(ln x f 在]1,0[上有意义且可积 ,2：将和式极限，表示成定积分.⎥⎦⎤⎢⎣⎡-++-+-∞→2222241241141lim n n n n n ⎰∑-=-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-++-+-=⎥⎦⎤⎢⎣⎡-++-+-=∞→∞→∞→1021222222222411)(41lim )(41)2(41)1(411lim 41241141lim dxx n ni n n n n n n n n n n i n n n 解第二节 定积分的性质、中值定理1.定积分性质2.中值定理对定积分的补充规定:（1）当b a =时，0)(=⎰ba dx x f ；（2）当b a >时，⎰⎰-=abb adx x f dx x f )()(.说明 在下面的性质中，假定定积分都存在，且不考虑积分上下限的大小．一、定积分性质和中值定理证⎰±ba dxx g x f )]()([i i i ni x g f ∆±=∑=→)]()([lim 10ξξλi i ni x f ∆=∑=→)(lim 10ξλii ni x g ∆±∑=→)(lim 10ξλ⎰=ba dx x f )(.)(⎰±ba dx x g ⎰±b a dx x g x f )]()([⎰=b a dx x f )(⎰±ba dx x g )(.（此性质可以推广到有限多个函数作和的情况）性质1⎰⎰=ba b a dx x f k dx x kf )()( (k 为常数).证⎰ba dx x kf )(ii ni x kf ∆=∑=→)(lim 10ξλi i n i x f k ∆=∑=→)(lim 1ξλii ni x f k ∆=∑=→)(lim 10ξλ.)(⎰=ba dx x f k 性质2⎰ba dx x f )(⎰⎰+=bcca dx x f dx x f )()(.补充：不论 的相对位置如何, 上式总成立.c b a ,,例 若,c b a <<⎰c a dx x f )(⎰⎰+=cb b a dx x f dx x f )()(⎰b a dx x f )(⎰⎰-=cb c a dxx f dx x f )()(.)()(⎰⎰+=bc ca dx x f dx x f （定积分对于积分区间具有可加性）假设bc a <<性质3dx b a ⋅⎰1dx ba⎰=a b -=.则0)(≥⎰dx x f ba. )(b a <证,0)(≥x f ,0)(≥ξ∴i f ),,2,1(n i =,0≥∆i x ,0)(1≥∆ξ∴∑=i i ni x f },,,max{21n x x x ∆∆∆= λi i ni x f ∆∴∑=→)(lim 1ξλ.0)(⎰≥=ba dx x f 性质4性质5如果在区间],[b a 上0)(≥x f ，例1 比较积分值dx e x⎰-20和dx x ⎰-20的大小.解令,)(x e x f x -=]0,2[-∈x ,0)(>x f ,0)(02>-∴⎰-dx x exdx ex⎰-∴2,02dx x ⎰->于是dx e x ⎰-2.20dx x ⎰-<性质5的推论：证),()(x g x f ≤ ,0)()(≥-∴x f x g ,0)]()([≥-∴⎰dx x f x g ba ,0)()(≥-⎰⎰ba ba dx x f dx x g 于是 dx x f ba ⎰)( dx x g ba ⎰≤)(.则dx x f ba ⎰)( dx x g ba ⎰≤)(. )(b a <如果在区间],[b a 上)()(x g x f ≤，（1）dx x f b a ⎰)(dx x f ba⎰≤)(.)(b a <证,)()()(x f x f x f ≤≤- ,)()()(dx x f dx x f dx x f ba ba ba ⎰⎰⎰≤≤-∴即dx x f ba ⎰)(dx x f ba⎰≤)(.说明： 可积性是显然的.|)(x f |在区间],[b a 上的性质5的推论：（2）设M 及m 分别是函数证,)(M x f m ≤≤ ,)(⎰⎰⎰≤≤∴ba ba b a Mdx dx x f dx m ).()()(a b M dx x f a b m ba -≤≤-⎰（此性质可用于估计积分值的大致范围）则 )()()(a b M dx x f a b m ba -≤≤-⎰.)(x f 在区间],[b a 上的最大值及最小值，性质6例2 估计积分dx x⎰π+03sin 31值的范围.解,sin 31)(3xx f +=],,0[π∈∀x ,1sin 03≤≤x ,31sin 31413≤+≤x ,31sin 31410030dx dx x dx ⎰⎰⎰πππ≤+≤.3sin 31403π≤+≤π∴⎰πdx x例3 估计积分dx xx⎰ππ24sin 值的范围.解,sin )(xx x f =2sin cos )(x x x x x f -='2)tan (cos x x x x -=⎥⎦⎤⎢⎣⎡∈2,4ππx ,0<)(x f 在]2,4[ππ上单调下降,,22)4(π=π=f M ,2)2(π=π=f m ,442π=π-π=-a b ,422sin 4224π⋅π≤≤π⋅π∴⎰ππdx x x .22sin 2124≤≤∴⎰ππdx x x 如果函数)(x f 在闭区间],[b a 上连续，上的平均值在],[)()(1b a x f dxx f a b ba⎰-则在积分区间],[b a 上至少存在一个点 ξ，使dx x f b a ⎰)())((a b f -=ξ. )(b a ≤≤ξ性质7（定积分中值定理）积分中值公式证Mdx x f a b m ba≤-≤∴⎰)(1)()()(a b M dx x f a b m ba -≤≤-⎰ 由闭区间上连续函数的介值定理知在区间],[b a 上至少存在一个点 ξ,)(1)(⎰-=ξbadx x f a b f dx x f ba ⎰)())((ab f -=ξ.)(b a ≤≤ξ即在区间],[b a 上至少存在一个点ξ，1. 积分中值公式的几何解释：xyoa b ξ)(ξf 使得以区间],[b a 为以曲线)(x f y =底边，为曲边的曲边梯形的面积等于同一底边而高为)(ξf 的一个矩形的面积。

广义积分的几个计算公式广义积分是指将拓展由单变量积分发展而来并用于多变量积分和有限元积分的变体，以帮助解决由分段函数和更宽泛形式的函数定义的积分问题。

其计算的公式如下：1.单变量积分：对于一元函数f（x），它的定积分为∫f (x) dx, 其结果为[ F(x ) + C], 其中C为常数，F(x)为原函数f (x )的积分函数。

2.多变量积分：对于二元函数f (x, y)，根据变量分别求积分，即∫f (x, y)d x∫f (x, y)d y, 其结果为[ F(x , y） + C], 其中C为常数，F(x , y)为原函数f (x , y )的积分函数。

3.向量积分：对于M元函数f（x1，x2，…，xM），将它视为一个向量，其积分可求为∫ ∫…∫f (x1，x2，…，xM) dx1dx2…dxM , 其结果为[ F(x1，x2，…，xM ) + C]，其中C为常数，F(x1，x2，…，xM )为原函数f (x1，x2，…，xM )的积分函数。

4.曲面积分：对于曲面f (x, y, z)，其积分可求为∫∫f (x，y，z) da, 其结果为[F (x，y，z) + C]，其中C为常数，F (x，y，z)为原函数f (x，y，z)的积分函数。

5.对象积分：用于计算实体表面和体积之间关系的积分，是为求解几何学问题而出现的，其积分形式为∫∫∫f (x，y，z) d v, 其结果为[F (x，y，z) + C]，其中C为常数，F (x，y，z)为原函数f (x，y，z)的积分函数。

综上所述，广义积分分为单变量积分、多变量积分、向量积分、曲面积分和对象积分等模式，它的计算公式均为[F ( x , y, ... , z )+C]，其中C为常数、[F ( x , y, ... , z )]为原函数f ( x , y, ... , z )的积分函数。

它可用于计算傅立叶级数和拉普拉斯积分等积分问题。

综上所述，可以看出，广义积分具有很好的应用价值，可以帮助解决很多积分问题。

积分常用公式一．基本不定积分公式：1． C x dx +=⎰2． ) 3．111++=⎰αααx dx x 1(-≠αC x dx x+=⎰ln 14．5．C aa dx a xx+=⎰ln )1,0(≠>a a C e dx e xx+=⎰6． 7．C x xdx +-=⎰cos sin C x xdx +=⎰sin cos 8．9．C x dx x xdx +==⎰⎰tan cos 1sec 22Cx dx x xdx +-==⎰⎰cot sin 1csc 2210． 11．C x xdx x +=⋅⎰sec tan sec Cx xdx x +-=⋅⎰csc cot csc 12．（或）C x dx x+=-⎰arcsin 11212arccos 11C x dx x+-=-⎰13．（或）C x dx x +=+⎰arctan 11212cot 11C x arc dx x +-=+⎰14．15．C x xdx +=⎰cosh sinh Cx xdx +=⎰sinh cosh 二．常用不定积分公式和积分方法：1．2．C x xdx +-=⎰cos ln tan Cx xdx +=⎰sin ln cot 3．4．C axa x a dx +=+⎰arctan 122C a x ax a ax dx ++-=-⎰ln 21225． 6．C x x xdx ++=⎰tan sec ln sec C x x xdx +-=⎰cot csc ln csc 7．8．C axx a dx +=-⎰arcsin22Ca x x a x dx +±+=±⎰2222ln 9．C a x a x a x dx x a ++-=-⎰arcsin 222222210．Ca x x a a x xdx a x +±+±±=±⎰2222222ln 2211．第一类换元积分法（凑微分法）：Cx F x t x d x f dx x x f dx x g +=='=⎰⎰⎰)]([)(])([)]([)()]([)(ϕϕϕϕϕϕ为为为为为为为为为为为为12．第二类换元积分法（典型代换：三角代换、倒代换、根式代换）：Cx F C t F dt t f dt t t g t x dxx g +=+=='=-⎰⎰⎰)]([)()()()]([)()(1ϕϕϕϕ为注：要求代换单调且有连续的导数，且“换元须还原”)(t ϕ13．分部积分法(典型题特征：被积函数是两类不同函数的乘积，且任何一个函数不能为另一个函数凑微分)⎰⎰-=vduuv udv 14．万能置换公式（针对三角有理函数的积分。

、定积分计算基本方法1牛顿一莱布尼兹公式：护0)=a,®(P )二b ，f ［®(t)］在［S P ］上连续，b pf f (x)dx = f f ［®(t)］®'(t)dt 。

注：条件3书上用较强的条件f(x) 在 ［a,b ］上连续且当"［sP ］时，护(t)的 值域不超出［a,b ］来代替。

实际上代换W (t)的值域可以超出［a,b ］，如上图。

bbbaudv =[uv]a - [vdu注意事项：1、被积函数含绝对值记号。

1 -<x <1 时，In xcO,|l nx|=-l nx ；当 1<x c e 时，In x>O,|l n x |= Inx 。

e1e2(l nxdx=f 1(T n x)dx +[l nxdx=2-- (分界点 x=1 处 ln x = 0) ； ；eba f (x)dx =F(x)a=F(b)-F(a) (t)2、定积分的换元法:设10④(t)&'(t)在［gP ］上连续, aa a 1 01 P例1：M ln x |dxe例2：|x-3|dx解： 4订 X —dx = 例3： 「J sin 3 x -!4 sin5 xdx 34[(3 - x)dx + ((X —3)dx= 5 20 30 3、定积分的分部积分法:解：当兀3 兀3 4 02 sin 2 xcosxdx + (sin 2x( -cosx)dx =-2、广义积分有推广的牛顿-莱布尼兹公式(1)如果f(x)在［a,b)上连续，f(b-O) = K ,原函数F(x)在［a,b ］上连续，贝U 仍有(2)如果f(x)在［a,址)上连续，f(x)的原函数F(x)适合lim F(x)存在记为F (畑)则-be d X例解： 0兀 J si n 3x-si n 5xdx = 3兀 9f sin 2X I cos b[f(x)dx =F(x) a4 = F(b-O)-F(a)仍有[f (x)dx = F (x) 产=F (址)-F(a)。

广义积分与应用广义积分是微积分中的重要概念，它是对函数在一定区间上的累积求和。

广义积分在数学和工程领域中有着广泛的应用，本文将介绍广义积分的基本概念和一些常见的应用。

一、广义积分的基本概念1.1 定积分的基本概念定积分是广义积分的一种特殊情况，用来求解函数在一个有限区间上的积分值。

定积分符号表示为∫，函数f(x)在[a,b]上的定积分表示为∫[a,b]f(x)dx。

1.2 不定积分的基本概念不定积分是对函数的原函数的求解，符号表示为∫f(x)dx。

不定积分存在一个常数项，因为对同一个函数而言，它的导函数是不唯一的。

1.3 广义积分的引入广义积分是对不可积函数或无界函数的积分概念进行推广，用于解决一些求和问题。

广义积分符号表示为∫，函数f(x)在区间[a, b]上的广义积分表示为∫[a, b]f(x)dx。

二、广义积分的计算方法2.1 瑕积分瑕积分是广义积分的一种形式，它处理无界函数或在某些点上发散的函数。

瑕积分的计算需要将无穷区间[a, b]划分成有限个有界子区间，并通过求解有界子区间上的定积分来求解广义积分。

2.2 收敛与发散广义积分可能会收敛或发散。

当广义积分的值存在有限的极限时，称其为收敛；当广义积分不存在有限极限时，称其为发散。

2.3 收敛级数收敛级数是广义积分的另一种形式，它是无穷序列求和的极限。

收敛级数可以表示为∑an = s，其中s为收敛和。

三、广义积分的应用领域3.1 几何学应用广义积分在几何学中有着广泛的应用，可以用于计算曲线长度、曲线与坐标轴所围成的面积、曲面面积和曲面体积等。

3.2 物理学应用在物理学中，广义积分可以用于求解质点或杆的质心、质量、转动惯量等重要物理量。

此外，广义积分还可以用于计算流体力学中的流量、质量、功率等。

3.3 统计学应用广义积分在统计学中也有一些应用，例如求解概率密度函数和累计分布函数等，这对于研究随机变量的概率分布及其性质非常重要。

3.4 工程学应用在工程学中，广义积分被广泛应用于求解电路中的电流、电压、功率等，并且还可以用于计算传热学中的热量、传热速率等。

广义积分计算公式广义积分是微积分中的一种重要概念，它是对实数区间上的函数进行积分的一种方法。

广义积分计算公式提供了一种计算广义积分的方法，它包括了不定积分和定积分两种形式。

在下面的文章中，我将详细介绍广义积分的计算公式和具体的计算方法。

首先，我们来看不定积分的计算公式。

不定积分是对函数进行积分而不指定上下限的形式，它可以表示为∫f(x)dx。

其中，f(x)表示要积分的函数。

不定积分的计算公式可以通过基本积分公式来得到。

常见的基本积分公式包括：1. ∫x^n dx = (x^(n+1))/(n+1) + C，其中n不等于-12. ∫1/x dx = ln，x， + C。

3. ∫e^x dx = e^x + C。

4. ∫sin(x) dx = -cos(x) + C。

5. ∫cos(x) dx = sin(x) + C。

这些基本积分公式是广义积分计算的基础，它们可以用来计算更加复杂的不定积分。

下面我们来看定积分的计算公式。

定积分是对函数在一个闭区间上进行积分，它可以表示为∫[a,b]f(x)dx。

其中f(x)表示要积分的函数，[a,b]表示积分的闭区间。

定积分的计算公式可以通过牛顿—莱布尼茨公式来得到。

牛顿—莱布尼茨公式为：∫[a,b] f(x)dx = F(b) - F(a)，其中F(x)为f(x)的一个原函数。

这个公式告诉我们，如果能够找到一个函数F(x)，使得它的导数等于f(x)，那么定积分的结果就等于F(b)-F(a)。

在实际计算中，很多函数并没有具体的原函数表达式，因此我们需要通过其他方法来计算定积分。

常见的方法包括换元法、分部积分法和凑微分法等。

换元法是指通过变量代换来简化积分的计算。

具体来说，我们可以将原函数的自变量进行适当的变换，使得积分变得更加容易计算。

常见的变量代换包括三角函数的代换、指数函数的代换和对数函数的代换等。

分部积分法是指通过将积分公式转化为乘法形式，然后使用乘法的公式进行计算。

定积分的广义积分定积分是微积分中的重要概念，它能够求出函数在一定区间内的面积或曲线长度等量值。

然而，不是所有函数都能够进行定积分，因为在某些情况下，函数可能在区间内出现无限大、无界、发散等情况。

这时，就需要引入广义积分的概念。

一、广义积分的定义广义积分是指函数在无限区间上的积分，它的定义分为以下两种情况：1. 第一类广义积分如果函数 f(x) 在区间a ≤ x ≤ ∞ 上 Riemann 可积，那么第一类广义积分可以定义为：$$ \int_a^\infty f(x) dx = \lim_{b \rightarrow \infty} \int_a^b f(x)dx $$其中，a 为下限，∞ 为上限，b 为上限的一个变量。

这个定义表示，当上限趋近于无穷大时，积分的值趋于一个有限值，那么这个积分就是收敛的。

如果这个极限不存在或为无穷大时，那么这个积分就是发散的。

2. 第二类广义积分如果函数在区间a ≤ x ≤ b 的一个子区间上发生无限大或无穷小的情况，那么就需要使用第二类广义积分的定义。

对于函数 f(x) 在区间a ≤ x ≤ b 上不连续，但在每个分割区间内仍然 Riemann 可积的情况，第二类广义积分可以定义为：$$ \int_a^b f(x)dx = \lim_{\epsilon_1 \rightarrow 0^+, \epsilon_2\rightarrow 0^+} \int_{a+\epsilon_1}^{c-\epsilon_2} f(x)dx $$其中，a 为下限，b 为上限，c 为 a 与 b 之间的某一点。

这个定义表示，当积分范围趋近于a 或b 时，积分的值趋于一个有限值，那么这个积分就是收敛的。

如果这个极限不存在或为无穷大时，那么这个积分就是发散的。

二、广义积分的应用广义积分在微积分中有着广泛的应用，例如在物理学和工程学中，它可以被用来计算无限长的线、面、体等的质量、电荷、热量等物理量。