程序变换技术

三电平逆变程序三电平逆变是一种常用的电力电子变换技术，可以将直流电源转换为交流电源，广泛应用于工业控制、电力传输和电动汽车等领域。

本文将介绍三电平逆变的原理、应用和优缺点。

一、三电平逆变的原理三电平逆变是一种多电平逆变技术，与传统的二电平逆变相比，具有更高的输出质量和更低的谐波含量。

其基本原理是通过控制逆变器的开关状态，将直流电源的电压转换为多个不同的电平，从而实现更接近正弦波形的交流输出。

在三电平逆变中，逆变器的输出电压可以取三个不同的电平值，分别为负最大值、零和正最大值。

通过合理控制逆变器的开关状态，可以将这三个电平按照一定的时序组合起来，从而实现近似正弦波形的输出电压。

在实际应用中，通常采用PWM（脉宽调制）技术来实现对逆变器开关状态的精确控制，以获得更高的输出质量。

二、三电平逆变的应用三电平逆变技术在工业控制、电力传输和电动汽车等领域有着广泛的应用。

其中，工业控制是三电平逆变最主要的应用领域之一。

在工业控制系统中，电动机是最常见的负载，而电动机的控制需要交流电源。

传统的二电平逆变无法提供质量较高的交流电源，而三电平逆变可以通过输出更接近正弦波形的电压，提高电动机的性能和效率。

三电平逆变还可以应用于电力传输领域。

在电力传输中，为了减小传输损耗，通常采用高压直流输电（HVDC）技术。

而在直流输电的终端，需要将直流电源转换为交流电源供给用户。

三电平逆变可以实现高质量的交流输出，提高电力传输的效率和稳定性。

随着电动汽车的快速发展，三电平逆变技术也得到了广泛应用。

电动汽车的动力系统通常由电池组和电动机组成，而电池组输出的是直流电，需要经过逆变器转换为交流电供给电动机。

采用三电平逆变技术可以提供更稳定、更高效的交流电源，提升电动汽车的性能和续航里程。

三、三电平逆变的优缺点三电平逆变相比传统的二电平逆变具有以下优点：1. 输出质量高：三电平逆变可以输出更接近正弦波形的交流电压，减小谐波含量，提高电力质量。

C语言矩阵变换程序实例C语言矩阵变换程序实例矩阵的计算主要是考虑下标之间的变换,下面就有店铺分享C语言矩阵变换程序实例，欢迎大家学习!本程序使用for循环嵌套的方式实现矩阵转置“计算”，实际程序并未发生计算。

经过简单的代码添加可让其从固定的2X3转置变为任意转置，有兴趣的`同学可以尝试修改代码。

源代码：#include //预处理指令：包含标准输入输出库int main(int argc,char* argv[]){int a[2][3],i,j; //定义二维数组用于存放数据，两个累加变量用于控制for循环printf("***请输入初始矩阵a的数据*** ");for(i=0;i<2;i++){ //循环嵌套，提示用户输入数据并标准化输入到二维数组for(j=0;j<3;j++){printf(">请输入a%d%d的值：",i+1,j+1);scanf("%d",&a[i][j]);}}printf("***初始矩阵a的数据输入完成，矩阵如下*** ");printf("******************** ");for(i=0;i<2;i++){ //将输入完成的二维数组输出for(j=0;j<3;j++){printf("%d ",a[i][j]);}printf(" ");}printf("******************** ");printf("****矩阵a的转置矩阵为**** ");//交换控制变量的嵌套位置再输出实现“转置”二维数组实际未变化for(j=0;j<3;j++){for(i=0;i<2;i++){printf("%d ",a[i][j]);}printf(" ");}printf("***powered by 局部变量***");return 0; //给操作系统返回0值来判定程序正确运行}。

傅里叶变换c程序傅里叶变换是一种将时域信号转换到频域的数学工具。

在C语言中，可以使用库函数来实现傅里叶变换。

以下是一个使用GNU Scientific Library (GSL)库进行傅里叶变换的简单C程序的示例。

请确保你已经安装了GSL库。

```c#include <stdio.h>#include <math.h>#include <gsl/gsl_fft_complex.h>#define N 64int main() {// 定义输入信号double data[2 * N];// 初始化输入信号（这里使用一个简单的正弦波作为例子）for (int i = 0; i < N; i++) {data[2 * i] = sin(2.0 * M_PI * i / N);data[2 * i + 1] = 0.0;}// 执行傅里叶变换gsl_fft_complex_radix2_forward(data, 1, N);// 打印变换结果printf("Original Signal\t\t\t\t\t\t\t\tTransformed Signal\n");for (int i = 0; i < N; i++) {printf("%f\t%f\t\t\t\t\t\t\t\t%f\t%f\n",data[2 * i], data[2 * i + 1],data[2 * i], data[2 * i + 1]);}return 0;}```上述程序使用了GSL库的`gsl_fft_complex_radix2_forward` 函数执行快速傅里叶变换（FFT）。

你需要确保在编译时链接GSL库。

例如，使用gcc编译时可以添加`-lgsl -lgslcblas -lm` 参数：```bashgcc your_program.c -o your_program -lgsl -lgslcblas -lm```此外，请注意，上述代码仅演示了傅里叶变换的基本使用。

ollvm高级用法-回复OLLVM（Obfuscator-LLVM）是一个基于LLVM框架的开源混淆器。

它通过对程序进行各种转换和变换来增加程序的复杂性和难以理解程度，从而提高程序的保护性能。

OLLVM的高级用法广泛应用于软件防护和安全领域，本文将以OLLVM的高级技术为主题，逐步回答关于OLLVM高级用法的问题。

1. 什么是OLLVM的高级用法？OLLVM的高级用法是指通过使用OLLVM的进阶技术和功能来进行更加强大和高级的混淆和保护。

这些高级用法包括更复杂的代码变换、控制流平坦化、随机数生成和填充、间接调用解析等技术，以增加程序的复杂性和混淆程度，从而使程序更难以逆向工程和分析。

2. OLLVM如何进行代码变换和控制流平坦化？代码变换是OLLVM的关键技术之一，它通过对程序的指令和基本块进行转换和重组，来改变程序的结构和逻辑关系。

控制流平坦化是其中一种常见的代码变换技术，它将程序的控制流图中的分支语句进行重排和重组，使得程序的控制流在执行过程中变得不可预测和难以理解。

3. OLLVM如何通过随机数生成和填充来增加混淆程度？通过使用随机数生成和填充技术，OLLVM可以在程序中引入大量的随机性和不确定性，从而增加逆向工程和分析的难度。

随机数生成可以用来生成随机的假数据或者随机的控制流路径，填充则可以用来填充无用的、冗余的指令，以增加代码的大小和复杂性。

4. OLLVM的间接调用解析是什么意思？在程序中，间接调用是指通过函数指针或函数引用来调用具体函数的一种方式。

间接调用解析是指通过分析程序中所有的间接调用，然后根据上下文和控制流动态解析出具体的调用目标。

这种技术可以增加程序的不确定性和难以理解程度，从而增加逆向工程和分析的难度。

5. OLLVM高级用法有哪些应用场景？OLLVM的高级用法广泛应用于软件防护和安全领域。

它可以保护软件免受恶意攻击和逆向工程，提高应用程序的安全性。

OLLVM高级用法适用于各种类型的软件，例如移动应用程序、嵌入式设备固件、游戏等。

单相dq变换锁相程序
单相dq变换锁相程序是现代电力电子技术中应用广泛的一种技术手段。

它主要是利用数学变换将交流电信号转化为直流信号进行控制，从而
实现对电力电子器件的精确控制。

具体而言，单相dq变换锁相程序包
含以下几个主要环节：
1. 相量测量
单相dq变换锁相程序首先需要测量电网电压的相量，从而确定系统的
相位差和频率等关键参数。

这一步通常需要使用传感器或计算方法，
在不同位置测量电压，然后将测量结果进行处理，得到电网电压的相
量值。

2. 变换运算
单相dq变换锁相程序的核心是变换运算。

它主要是利用dq变换将三
相交流电信号转换为两个等效的直流信号，即d轴信号和q轴信号。

这样可以使控制系统更加简单精确，提高其响应速度和控制精度。

3. PI控制
单相dq变换锁相程序在进行控制过程中，需要对d轴和q轴信号进行
精确的控制。

通常采用PI控制算法，通过调整PI控制器的参数来控
制电力电子器件的输出电流，从而达到控制的目的。

4. 输出控制
单相dq变换锁相程序最终的目的是控制电力电子器件的输出电流和电
压等参数。

根据电路的结构和控制要求，选择合适的输出控制方法，
使得控制系统能够按照预定要求进行运行，达到控制目标。

总之，单相dq变换锁相程序是电力电子技术中非常重要的一种技术手段。

其基本原理是利用数学变换将交流电信号转化为直流信号进行控制，从而达到精确控制电力电子器件的目的。

通过相量测量、变换运算、PI控制和输出控制等环节，可以有效地实现该技术手段的应用。

dq 变换c语言源程序DQ 变换（也被称为DIF-RADIX 变换）是一种在离散傅里叶变换（DFT）算法中广泛使用的方法。

DQ 变换可以将一个长度为N 的复数序列分解为多个较小长度的序列，从而减少计算复杂度。

在本文档中，我们将介绍DQ 变换的原理和一份简单的 C 语言源程序，用于实现DQ 变换。

1. 原理介绍在离散傅里叶变换中，一个长度为N 的复数序列通过计算N 个复数的和差运算得到新的复数序列，以实现频域和时域之间的转换。

而DQ 变换则通过将长度为N 的复数序列分解为多个长度为M（M < N）的子序列，然后对每个子序列进行DQ 变换，最终将它们合并为最后的结果。

2. DQ 变换的算法流程（1）将长度为N 的输入序列进行奇偶分组，即将输入序列按照奇偶位置分为两部分。

（2）对奇偶分组后的序列分别进行长度为M 的DQ 变换。

（3）将变换后的两个子序列合并为最终的变换结果。

3. C 语言源程序实现#include <stdio.h>#include <math.h>#define N 8 // 输入序列的长度#define M 2// DQ 变换的子序列长度typedef struct { double real; double imag;} Complex;void DQ(Complex x[], int n) { if (n == M) { /* 长度为M 的DQ 变换，可使用其他算法实现*/ // TODO: 实现长度为M 的DQ 变换} else { int j; Complex Wn = {1, 0}; Complex W = {cos(2 * M_PI / n), sin(2 * M_PI / n)};Complex tmp; Complex *y = malloc(sizeof(Complex) * n);/* 奇偶分组*/ Complex *even = malloc(sizeof(Complex) * n/2); Complex *odd =malloc(sizeof(Complex) * n/2); for (int i = 0; i < n; i += 2) { even[i/2] = x[i]; odd[i/2] =x[i+1]; }/* 递归计算子序列*/ DQ(even, n/2); DQ(odd, n/2);/* 合并子序列*/ for (int k = 0; k < n/2; k++) { tmp = odd[k] * Wn; y[k] = even[k] + tmp; y[k+n/2] = even[k] - tmp;Wn = Wn * W; }/* 将结果拷贝回x[] */ for (j = 0; j < n; j++) { x[j] = y[j]; }free(y); free(even);free(odd); }}int main() { Complex x[N] = { {1, 0}, {2, 0}, {3, 0}, {4, 0}, {5, 0}, {6, 0}, {7, 0}, {8, 0} };DQ(x, N);printf("DQ 变换结果：\n"); for (int i = 0; i < N; i++) { printf("x[%d] = %.2f + %.2fi\n", i, x[i].real,x[i].imag); }return 0;}4. 程序说明上述的C 语言源程序实现了一个简单的DQ 变换算法。

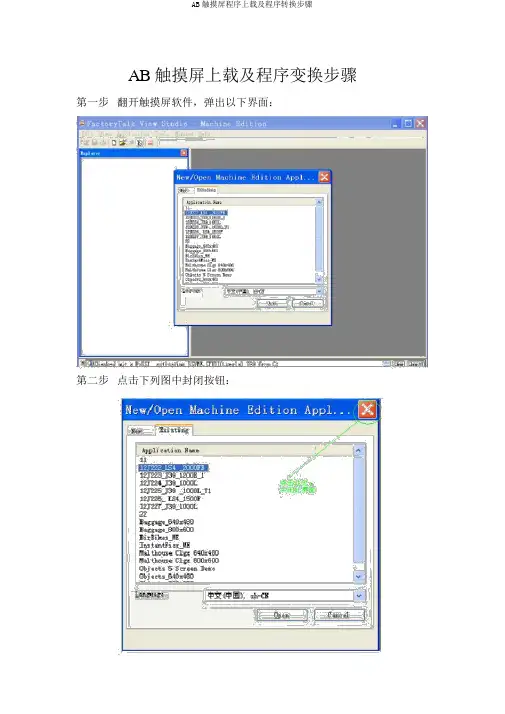
AB触摸屏上载及程序变换步骤第一步翻开触摸屏软件，弹出以下界面：第二步点击下列图中封闭按钮：封闭后显示下边界面：第三步点击下边的界面中标明的地方:点击上图中的地点后，弹出下边界面（详细操作在图中已经用红色标明）：选择上图中的地点后，下一步操作以下列图中红色标志的地点进行操作：选中触摸屏所对应的地点后，进行下一步操作以下列图所示：点击上图中所标标明的地点后弹出下边界面：选中对话框中的文件，点击OK，以下列图所示：接着进行下一步操作，以下列图中绿色说明所示：点击上图中绿色所说明处后弹出下边对话框：弹出的界面为上载过来的触摸屏程序所要储存的地点，详细寄存在什么地点，自己依据状况决定，选择好所要寄存的地点后点击“确立“按钮，显示下边界面：最后点击“ Upload”按钮即可进行程序上载。

触摸屏程序上载达成后，是一个触摸屏上显示的形式，需要进行变换，变换步骤以下：第一步点击翻开触摸屏软件，翻开界面以下列图所示：第二步点击下列图中封闭按钮：封闭后显示下边界面：第三步点击下边的界面中标明的地方:点击上图中标明的地方弹出下边界面：选择上图中所说明的地点点击弹出下边界面：选择下列图中所标明的地点：选择上图中红色说明的地点点击下一步会弹出下边的界面：点击下列图中所说明的地点：点击上图中所说明的地点，弹出下边界面：选择上边所“上载”程序所寄存的地点，（就是上载程序达成后所寄存的那个程序），找到选中后点击“翻开”按钮，弹出下边界面：点击“达成”按钮即可达成变换（申明：变换需要时间请等候不要急于封闭）。

此外解说说明以下列图所示：上图中选择不一样的操作进行不一样的操作。

比如：选择“备份文件”点击下一步后弹出下边界面：选中相应的文件点击下一步弹出下边界面：下一步以下图：选择好所要储存的路径后点击“达成”按钮，即可达成程序备份（备份需要时间请等候一会）。

小波变换matlab程序小波变换是一种信号处理技术，它可以将信号分解成不同频率的成分，并且可以在不同时间尺度上进行分析。

在Matlab中，可以使用内置的小波变换函数来实现这一技术。

下面是一个简单的小波变换Matlab程序示例：matlab.% 生成一个示例信号。

t = 0:0.001:1; % 时间范围。

f1 = 10; % 信号频率。

f2 = 50; % 信号频率。

y = sin(2pif1t) + sin(2pif2t); % 信号。

% 进行小波变换。

[c, l] = wavedec(y, 3, 'db1'); % 进行3层小波分解，使用db1小波基函数。

% 重构信号。

yrec = waverec(c, l, 'db1'); % 使用小波系数和长度进行信号重构。

% 绘制原始信号和重构信号。

subplot(2,1,1);plot(t, y);title('原始信号');subplot(2,1,2);plot(t, yrec);title('重构信号');这个程序首先生成了一个包含两个频率成分的示例信号，然后使用`wavedec`函数对信号进行小波分解，得到小波系数和长度。

接着使用`waverec`函数对小波系数和长度进行信号重构，最后绘制了原始信号和重构信号的对比图。

小波变换在信号处理、图像处理等领域有着广泛的应用，可以用于信号去噪、特征提取、压缩等方面。

通过Matlab中的小波变换函数，我们可以方便地进行小波分析和处理，从而更好地理解和利用信号的特性。

PIC16F917单片机c语言源程序ad变换，pwm输出，数码显示//说明：完整的PIC16F917编写的c语言程序，通过编译，内容包含有ad变换，pwm输出，数码显示（通过串口移位显示），串行口通讯等#include;#define uchar unsigned char#define uint unsigned int__CONFIG(0x20e4);#define choose1 RC4#define choose2 RC3#define power_high RA6#define power_low RA4#define relay_w RE2#define relay_v RB5#define relay_u RA0#define data1 RD0#define clk1 RA7#define bell RD3#define power_supply RD6#define pha RB2#define phb RB3#define phc RB4#define spa RB0#define spb RB1#define up RC1#define down RC2#define up1 RD2#define down1 RC0#define safe RD7#define start RD5 #define speeder RD4 #define KDF RD1#define test_num1 1 #define test_num2 2 #define test_num3 3 #define test_num4 4 #define test_num5 5 #define test_num6 6 #define test_num7 7 #define test_num8 8 #define test_num9 9 #define test_num10 10#define test_num11 11 #define test_num12 12 #define test_num13 13 #define test_num14 14 #define test_num15 15 #define test_num16 16 #define test_num17 17 #define test_num18 18 #define test_num19 19 #define test_num20 20 #define test_num21 21 #define test_num22 22 #define test_num23 23 #define test_num24 24 #define test_num25 25 #define test_num26 26 #define test_num27 27 #define test_num28 28 #define hold 29#define stop 30#define setout 31#define test_err 32#define power 33#define TEST_5045 34#define TEST_5046 35#define TEST_5055B 36#define power1 37#define setout1 38#define setout2 39#define disp_refresh 100const uchartable[]={0xfc,0x60,0xda,0xf2,0x66,0xb6,0xbe,0xe0, 0xfe,0xf6,0xee,0xfe,0x9c,0xfc,0x9e,0x8e,2,0x10,0x 80,4};const uchartable1[]={0xfd,0x61,0xdb,0xf3,0x67,0xb7,0xbf,0xe1 ,0xff,0xf7,0xef,0xff,0x9d,0xfd,0x9f,0x8f,0x6f,0x0 d};ucharkeyvalue=1,keystate=0,keypull=0,status=setout,rcd ata1=0x55,rcdata2=0x55,rcdata3=0x55,status2=0; ucharerr_status=0,disp_run=0,ad_test=0,test15_tmp1=0,t est15_tmp2=0,test15_tmp3=0,test15_tmp4=0,disp_mod=0,disp_hold=0;uint rcdata,disp_time1=0,ad_data1,ad_data2; volatile unsigned intkeytime=0,bell_time=0,test_time=0,err_time=0,disp _time=0,tx_time=0;void disp(uchar num1,uchar num2,uchar num3); // 76usvoid disp10(uchar j); // 314usvoid keyscan(void);void key1(void);void init(void);void delaye(uint x);void outpwm(uchar x);void addisp(uint a);void addisp_8(uchar a);void disp20(uchar i,uchar j);void disp16(uint j);void err_disp(uchar j);void disp21(uchar i,uchar j);uint ad(uchar x);//3次加和一个除法 87usvoid main(){uchar tx_conut=0;init();while(1){if(status==setout1){if(disp_time>;disp_refresh){disp(table[18],table[18],table[18]);disp_time=0;}power_supply=0;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;spa=1;spb=1;pha=1;phb=1;phc=0;up=0;down=0;safe=0; up1=0;down1=0;}else if(status==setout2){if(disp_time>;disp_refresh){disp(table[19],table[19],table[19]);disp_time=0;}power_supply=0;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;spa=1;spb=1;pha=1;phb=1;phc=0;up=0;down=0;safe=0; up1=0;down1=0;}else if(status==setout){if(disp_time>;disp_refresh){disp(table[16],table[16],table[16]);disp_time=0;}power_supply=0;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;spa=1;spb=1;pha=1;phb=1;phc=0;up=0;down=0;safe=0; up1=0;down1=0;// TRISC7=0;// RC7=1;// speeder=1;if(keypull==1){bell=0;bell_time=0;keypull=0;status=power1;test_time=0;}}else if(status==power1){if(status2==TEST_5055B){TRISC7=1;TXSTA=0x26;RCSTA=0x90;SPBRG=103; //4.8k波特率power_supply=1;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;spa=1;spb=1;pha=1;phb=1;phc=0;up=0;down=0;safe=0; up1=0;down1=0;speeder=1;if(tx_time>;50&&TRMT==1){if(tx_conut==0){TXREG=0xfe;tx_time=0;tx_conut=1;}else if(tx_conut==1){TXREG=0xfd;tx_time=0;tx_conut=2;}else if(tx_conut==2){TXREG=0xfc;tx_time=0;tx_conut=3;}else if(tx_conut==3){TXREG=0xfb;tx_time=0;tx_conut=4;}else if(tx_conut==4){TXREG=0xfa;tx_time=0;tx_conut=0;}}if(rcdata1==0xaa)status=power;if(test_time>;1500)status=setout2; }elseif(status2==TEST_5046||status2==TEST_5045)status= power;}else if(status==power){power_supply=1;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;spa=1;spb=1;pha=1;phb=1;phc=0;up=0;down=0;safe=0; up1=0;down1=0;if(disp_time>;disp_refresh){disp(table[17],table[17],table[17]);disp_time=0;}if(status2==TEST_5046||status2==TEST_5045){TRISC7=0;RC7=1;speeder=1;}if(keypull==1){bell=0;bell_time=0;keypull=0;status=test_num1;TRISC7=1;TXSTA=0x26;RCSTA=0x90;SPBRG=103; //4.8k波特率test_time=0;disp_run=1;disp_time1=0;ad_test=1;ADCON0=0x85; //通道1ADCON1=0x50;}}else if(status==test_num1){spa=1;spb=1;pha=1;phb=1;phc=1;up=1;down=1;safe=1;up1=0;down1=0;power_supply=1;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;speeder=1;if(test_time>;100&&test_time;1000){status=test_err;err_status=1;err_time=0;disp_hold=1;}}else if(status==test_num2){spa=0;spb=0;pha=0;phb=0;phc=0;up=0;down=0;safe=0; up1=0;down1=0;power_supply=1;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;speeder=1;if(test_time>;100&&test_time;1000){status=test_err;err_status=2;err_time=0;disp_hold=1;}}else if(status==test_num3){if(status2==TEST_5046){spa=1;spb=1;pha=1;phb=0;phc=0;up=1;down=1;safe=1; up1=1;down1=1;power_supply=1;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;speeder=1;if(test_time>;100&&test_time;1000){status=test_err;err_status=3;err_time=0;disp_hold=1;}}else if(status2==TEST_5055B||status2==TEST_5045) {outpwm(200);test_time=0;status=test_num5;}}else if(status==test_num4){spa=0;spb=0;pha=0;phb=0;phc=0;up=0;down=0;safe=0; up1=0;down1=0;power_supply=1;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;speeder=1;if(test_time>;100&&test_time;1000){status=test_err;err_status=4;err_time=0;disp_hold=1;}}else if(status==test_num5){speeder=0;power_supply=1;power_high=0;power_low=0 ;relay_u=0;relay_v=0;relay_w=0;spa=1;spb=0;pha=0;phb=0;phc=0;up=0;down=0;safe=0; up1=0;down1=0;if(test_time>;100&&test_time;172&&rcdata1;172&&rc data2;172&&rcdata3;1000){status=test_err;err_status=5;err_time=0;disp_hold=1;}}else if(status==test_num6){speeder=0;power_supply=1;power_high=0;power_low=0 ;relay_u=0;relay_v=0;relay_w=0;spa=1;spb=0;pha=0;phb=0;phc=0;up=0;down=0;safe=0; up1=0;down1=0;if(test_time>;100&&test_time;101&&rcdata1;101&&rc data2;101&&rcdata3;1000){status=test_err;err_status=6;err_time=0;disp_hold=1;}}else if(status==test_num7){speeder=0;power_supply=1;power_high=0;power_low=0 ;relay_u=0;relay_v=0;relay_w=0;spa=1;spb=0;pha=0;phb=0;phc=0;up=0;down=0;safe=0; up1=0;down1=0;if(test_time>;100&&test_time;70&&rcdata1;70&&rcda ta2;70&&rcdata3;1000){status=test_err;err_status=7;err_time=0;disp_hold=1;}}else if(status==test_num8){speeder=0;power_supply=1;power_high=0;power_low=0 ;relay_u=0;relay_v=0;relay_w=0;spa=1;spb=0;pha=0;phb=0;phc=0;up=0;down=0;safe=0; up1=0;down1=0;if(test_time>;100&&test_time;14&&rcdata1;14&&rcda ta2;14&&rcdata3;1000){status=test_err;err_status=8;err_time=0;disp_hold=1;}}else if(status==test_num9) //2.4---2.53{if(test_time;=200&&test_time;=500&&test_time;=500 &&test_time;500&&ad_data1;500&&ad_data2;=1100) {status=test_err;err_status=9;err_time=0;ADON=0;ad_test=0;disp_mod=1;}}}else if(status==test_num10){if(test_time;=200&&test_time;=500&&test_time;=500 &&test_time;500&&ad_data1;500&&ad_data2;=1100) {status=test_err;err_status=10;err_time=0;ADON=0;ad_test=0;disp_mod=1;}}}else if(status==test_num11){if(test_time;=200&&test_time;=500&&test_time;=500 &&test_time;500&&ad_data1;500&&ad_data2;=1100){status=test_err;err_status=11;err_time=0;ADON=0;ad_test=0;disp_mod=1;}}}else if(status==test_num12) //+u,-V{if(test_time;=1000&&test_time;1000){spa=0;spb=1;p ha=1;phb=0;}elseif(test_time;1005){spa=0;spb=1;pha=1;phb=1;}elseif(test_time;1015){spa=0;spb=1;pha=1;phb=0;}ad_data1=0;}elseif(test_time>;=1100&&test_time;1100&&test_time;14 00&&ad_data1>;473&&ad_data1;2200){status=test_err;err_status=12;err_time=0;// SPEN=0;// CREN=0;// TRISC7=0;// RC7=1;ADON=0;ad_test=0;disp_mod=1;}}}else if(status==test_num13) //+U,-v{if(test_time;=1000&&test_time;1000){spa=0;spb=1;p ha=1;phb=0;}elseif(test_time;1005){spa=0;spb=1;pha=1;phb=1;}elseif(test_time;1015){spa=0;spb=1;pha=1;phb=0;}ad_data1=0;}elseif(test_time>;=1100&&test_time;1100&&test_time;14 00&&ad_data1>;534&&ad_data1;2200){status=test_err;err_status=13;err_time=0;// SPEN=0;// CREN=0;// TRISC7=0;// RC7=1;ADON=0;ad_test=0;disp_mod=1;}}}else if(status==test_num14) //+v,-U{if(test_time;=1000&&test_time;1000){spa=0;spb=1;p ha=1;phb=0;}elseif(test_time;1005){spa=0;spb=1;pha=1;phb=1;}elseif(test_time;1015){spa=0;spb=1;pha=1;phb=0;}}else if(test_time>;=1100&&test_time;1100){spa=1;spb=1;pha=0;phb=1;power_supply=1;power_high=1;power_low=0;relay_u=1 ;relay_v=0;relay_w=0;speeder=0;phc=0;up=0;down=0;safe=0;up1=0;down1=0;if(test_time>;1400&&ad_data1>;473&&ad_data1;2200) {status=test_err;err_status=14;err_time=0;// SPEN=0;// CREN=0;// TRISC7=0;// RC7=1;ADON=0;ad_test=0;disp_mod=1;}}}else if(status==test_num15) //+V,-u{if(test_time;=1000&&test_time;1000){spa=0;spb=1;p ha=1;phb=0;}elseif(test_time;1005){spa=0;spb=1;pha=1;phb=1;}elseif(test_time;1015){spa=0;spb=1;pha=1;phb=0;} }elseif(test_time>;=1100&&test_time;1100&&test_time;14 00&&ad_data1>;534&&ad_data1;2200){status=test_err;err_status=15;err_time=0;// SPEN=0;// CREN=0;/// TRISC7=0;// RC7=1;ADON=0;ad_test=0;disp_mod=1;}}}else if(status==test_num16) //-W,+v{if(test_time;=1000&&test_time;1000){spa=0;spb=1;p ha=1;phb=0;}elseif(test_time;1005){spa=0;spb=1;pha=1;phb=1;}elseif(test_time;1015){spa=0;spb=1;pha=1;phb=0;} }elseif(test_time>;=1100&&test_time;1100&&test_time;14 00&&ad_data1>;473&&ad_data1;2200){status=test_err;err_status=16;err_time=0;// SPEN=0;// CREN=0;// TRISC7=0;// RC7=1;ADON=0;ad_test=0;disp_mod=1;}}}else if(status==test_num17) //+W-v{if(test_time;=1000&&test_time;1000){spa=0;spb=1;p ha=1;phb=0;}elseif(test_time;1005){spa=0;spb=1;pha=1;phb=1;}elseif(test_time;1015){spa=0;spb=1;pha=1;phb=0;}ad_data1=0;}else if(test_time>;=1100&&test_time;1100){spa=1;spb=1;pha=0;phb=0;power_supply=1;power_high=0;power_low=1;relay_u=0 ;relay_v=0;relay_w=1;speeder=0;phc=0;up=0;down=0;safe=0;up1=0;down1=0;if(test_time>;1400&&ad_data1>;534&&ad_data1;2200) {status=test_err;err_status=17;err_time=0;// SPEN=0;// CREN=0;// TRISC7=0;// RC7=1;ADON=0;ad_test=0;disp_mod=1;}}}else if(status==test_num18) //+v,-U{if(test_time;=1000&&test_time;1000){spa=0;spb=1;p ha=1;phb=0;}elseif(test_time;1005){spa=0;spb=1;pha=1;phb=1;}elseif(test_time;1015){spa=0;spb=1;pha=1;phb=0;}ad_data1=0;}else if(test_time>;=1100&&test_time;1100){spa=1;spb=1;pha=0;phb=1;power_supply=1;power_high=1;power_low=0;relay_u=1 ;relay_v=0;relay_w=0;speeder=0;phc=0;up=0;down=0;safe=0;up1=0;down1=0;if(test_time>;1400&&rcdata1>;115&&rcdata1;2200) {status=test_err;err_status=18;err_time=0;SPEN=0;CREN=0;// TRISC7=0;// RC7=1;// ADON=0;// ad_test=0;}}}else if(status==test_num19) //+U,-v{if(test_time;=1000&&test_time;1000){spa=0;spb=1;p ha=1;phb=0;}elseif(test_time;1005){spa=0;spb=1;pha=1;phb=1;}elseif(test_time;1015){spa=0;spb=1;pha=1;phb=0;}ad_data1=0;}elseif(test_time>;=1100&&test_time;1100&&test_time;14 00&&rcdata1>;130&&rcdata1;2200){status=test_err;err_status=19;err_time=0;SPEN=0;CREN=0;// TRISC7=0;// RC7=1;// ADON=0;}}}else if(status==test_num20) //-W,+v{if(test_time;=1000&&test_time;1000){spa=0;spb=1;pha=1;phb=0;}else if(test_time;1005){spa=0;spb=1;pha=1;phb=1;} else if(test_time;1015){spa=0;spb=1;pha=1;phb=0;} ad_data1=0;}elseif(test_time>;=1100&&test_time;1100&&test_time;1400&&rcdata1>;115&&rcdata1;2200){status=test_err;err_status=20;err_time=0;SPEN=0;CREN=0;// RC7=1;// ADON=0;// ad_test=0;}}}else if(status==test_num21) //+W-v{if(test_time;=1000&&test_time;1000){spa=0;spb=1;p ha=1;phb=0;}elseif(test_time;1005){spa=0;spb=1;pha=1;phb=1;}elseif(test_time;1015){spa=0;spb=1;pha=1;phb=0;}ad_data1=0;}else if(test_time>;=1100&&test_time;1100){spa=1;spb=1;pha=0;phb=0;power_supply=1;power_high=0;power_low=1;relay_u=0 ;relay_v=0;relay_w=1;speeder=0;phc=0;up=0;down=0;safe=0;up1=0;down1=0;if(test_time>;1400&&rcdata1>;130&&rcdata1;2200) {status=test_err;err_status=21;err_time=0;SPEN=0;CREN=0;// TRISC7=0;// RC7=1;// ADON=0;// ad_test=0;}}}else if(status==test_num22){if(status2==TEST_5055B){if(test_time;900&&test_time;700&&ad_data1>;490&&a d_data1;1500){status=test_err;err_status=22;err_time=0;ADON=0;ad_test=0;disp_mod=1;}}elseif(status2==TEST_5046||status2==TEST_5045)status= test_num26;}else if(status==test_num23){if(test_time;900&&test_time;700&&ad_data1>;490&&a d_data1;1500){status=test_err;err_status=23;err_time=0;ADON=0;ad_test=0;disp_mod=1;}}else if(status==test_num24){if(test_time;900&&test_time;700&&ad_data1>;490&&a d_data1;1500){status=test_err;err_status=24;err_time=0;ADON=0;ad_test=0;disp_mod=1;}}else if(status==test_num25){if(test_time;900&&test_time;700&&ad_data1>;490&&a d_data1;1500){status=test_err;err_status=25;err_time=0;ADON=0;ad_test=0;disp_mod=1;}}else if(status==test_num26){speeder=0;power_supply=1;power_high=0;power_low=0 ;relay_u=0;relay_v=0;relay_w=0;speeder=0;KDF=0; spa=1;spb=0;pha=1;phb=0;if(test_time>;100&&test_time;240&&rcdata;1000) {status=test_err;err_status=26;err_time=0;disp_hold=1;}}else if(status==test_num27){speeder=0;power_supply=1;power_high=0;power_low=0 ;relay_u=0;relay_v=0;relay_w=0;speeder=0;KDF=0; spa=1;spb=0;pha=0;phb=1;if(test_time>;200&&test_time;220&&rcdata;400) {status=test_err;err_status=27;err_time=0;SPEN=0;CREN=0;// TRISC7=0;// RC7=1;// ADON=0;}}else if(status==test_num28){if(status2==TEST_5046){disp_run=0;power_supply=1;power_high=0;power_low= 0;relay_u=0;relay_v=0;relay_w=0;speeder=0;KDF=0; spa=0;spb=0;pha=0;phb=1;test15_tmp3=rcdata1;test15_tmp4=rcdata2;if(test_time>;100){if((test15_tmp3&0x20)==0)test15_tmp1=test15_tmp3; else test15_tmp2=test15_tmp3;if((test15_tmp4&0x20)==0)test15_tmp1=test15_tmp4; else test15_tmp2=test15_tmp4;disp20(test15_tmp1,test15_tmp2);}}else if(status2==TEST_5045){disp_run=0;power_supply=1;power_high=0;power_low= 0;relay_u=0;relay_v=0;relay_w=0;speeder=0;KDF=0; spa=0;spb=0;pha=0;phb=1;test15_tmp3=rcdata1;test15_tmp4=rcdata2;if(test_time>;100){if((test15_tmp3&0x20)==0)test15_tmp1=test15_tmp3; else test15_tmp2=test15_tmp3;if((test15_tmp4&0x20)==0)test15_tmp1=test15_tmp4; else test15_tmp2=test15_tmp4;disp21(test15_tmp1,test15_tmp2);test_time=0;}}else if(status2==TEST_5055B)status=setout1;}else if(status==test_err){disp_run=0;//power_supply=0;power_high=0;power_low=0;relay_u=0 ;relay_v=0;relay_w=0;speeder=0;KDF=0;speeder=0; if(disp_hold==1){if(err_status==26){power_supply=1;power_high=0;power_low=0;relay_u= 0;relay_v=0;relay_w=0;speeder=0;KDF=0;speeder=0;} else{power_supply=1;power_high=0;power_low=0;relay_u= 0;relay_v=0;relay_w=0;speeder=0;KDF=0;speeder=1;} }if(disp_hold==0){power_supply=0;power_high=0;power_low=0;relay_u= 0;relay_v=0;relay_w=0;speeder=0;KDF=0;speeder=0;} if(err_time;disp_refresh){err_disp(err_status);disp_time=0;}}else if(err_time;1000){if(disp_time>;disp_refresh){if(disp_mod==1){addisp(ad_data1);disp_time=0;}else{disp10(rcdata1);disp_time=0;}}}else if(err_time>;2000)err_time=0; }}}void init(){/*PORTA *//*RA0 relay_w 0 *//*RA1 vol 1 *//*RA2 +5V 1 *//*RA3 TYJ 1 *//*RA4 power_low 0 *//*RA5 SX 1 *//*RA6 power_high 0 *//*RA7 CLK1 0 */TRISA=0x2e; //0010 1110ANSEL=0x7e; //模拟输入PORTA=0;/*PORTB *//*RB0 SPA *//*RB1 SPB *//*RB2 PHA *//*RB3 PHB *//*RB4 PHC *//*RB5 ralay_v *//*RB6 CLK *//*RB7 DATA */TRISB=0xc0; //1100 0000,rb0--rb5输出，rb6、rb7输入PORTB=0;/*PORTC *//*RC0 DOWN1 *//*RC1 UP *//*RC2 DOWN *//*RC3 choose2 *//*RC4 choose1 *//*RC5 PWM *//*RC6 TXD *//*RC7 RXD */TRISC=0x58; //0101 1000PORTC=0x80; //1000 0000/*PORTD*//*RD0 DATA1 *//*RD1 KFD *//*RD2 up1 *//*RD3 bell *//*RD4 speeder *//*RD5 start *//*RD6 power_supply *//*RD7 safe */TRISD=0x20; //0010 0000PORTD=0x18; //0001 1000/*PORTE*//*RE0 DF *//*RE1 JX *//*RE2 relay_u *//*RE3 VPP */TRISE=0xb; //0000 1011,全输入RE2=0;OSCCON=0xfe; //时钟选择8mhz，内部振荡器VLCDEN=0;OPTION=0xc3;LCDEN=0;CMCON0=7;CCP2CON=0;ADCON1=0x50;TMR0=7;PEIE=1;T0IE=1;GIE=1;if(choose1==0&&choose2==1)status2=TEST_5045; if(choose1==1&&choose2==1)status2=TEST_5046; if(choose1==1&&choose2==0)status2=TEST_5055B; }void keyscan(){if(!start&&keyvalue){keyvalue=0;keytime=0;}if(start&&!keyvalue){keyvalue=1;keytime=0;}}void key1(){if(keystate==0){if(keyvalue==0&&keytime>;10) {keystate=1;keypull=1;keytime=0;}}else if(keystate==1){if(keyvalue==1&&keytime>;10) {keystate=0;keytime=0;}}else keystate=0;}void interrupt tm0(){uint int_i;if(bell_time>;50)bell=1; if(T0IF){keyscan();key1();keytime++;bell_time++;err_time++;test_time++;disp_time++;disp_time1++;tx_time++;if(ad_test==1){if(GODONE==0){// ad_data3=ad_data2; ad_data2=ad_data1;int_i=ADRESH;ad_data1=ADRESL|int_i;110)disp_time=0; if(disp_time1==100){disp10(status);disp_time1=0;}}T0IF=0;TMR0=7;}}void disp(uchar num1,uchar num2,uchar num3) {uchar i;uchar num_tmp1,num_tmp2;// cs1=0; //关闭显示// clr=0; //清除74ls164数据// clr=1;clk1=0; //上升沿移位num_tmp1=num1;for(i=8;i>;0;i--){num_tmp2=num_tmp1;num_tmp2=num_tmp2&0x01; if(num_tmp2==1)data1=1;elsedata1=0;clk1=1;clk1=0;num_tmp1=num_tmp1>;>;1; }num_tmp1=num2;for(i=8;i>;0;i--){num_tmp2=num_tmp1;num_tmp2=num_tmp2&0x01; if(num_tmp2==1)data1=1;elsedata1=0;clk1=1;clk1=0;。

概述1. Matlab是一个强大的数学软件，其图形用户界面（GUI）设计能力使得用户可以方便地通过图形界面来进行各种数学计算和数据处理。

2. 快速傅里叶变换（FFT）是一种高效的算法，用于将时域信号转换为频域信号，广泛应用于信号处理、通信系统、图像处理等领域。

Matlab GUI设计快速傅里叶变换FFT程序的重要性3. Matlab GUI设计能够使得用户通过交互式界面来输入数据、调整参数，直观地观察到FFT的结果，提高了用户的使用体验和操作便捷性。

4. 通过GUI设计FFT程序，可以为用户提供一种更加直观、友好的工具，让用户更方便地进行信号分析和处理。

Matlab GUI设计快速傅里叶变换FFT程序的步骤5. 确定FFT程序的功能和界面设计的需求：确定FFT程序需要实现的功能，包括输入信号、选择窗函数、设置采样点数等。

6. 创建Matlab GUI界面：利用Matlab的GUIDE工具或手动编写代码来创建GUI界面，包括按钮、文本框、滑动条等控件。

7. 编写FFT算法：利用Matlab内置的FFT函数或手动编写FFT算法，实现信号的快速傅里叶变换。

8. 连接界面和算法：编写Matlab代码，将GUI界面和FFT算法进行连接，使得用户输入参数后，能够实时进行FFT计算，并显示结果。

Matlab GUI设计快速傅里叶变换FFT程序的关键技术9. Matlab GUI的布局设计：合理布局界面，使得用户能够清晰地理解各个控件的作用和功能，方便操作。

10. 参数输入和设置：设计输入框、下拉框等控件，使得用户可以输入参数并进行设置，如输入信号、选择窗函数、设置采样点数等。

11. FFT结果的可视化：设计图表控件，能够直观地显示FFT的结果，如时域信号、频谱图、相位图等。

12. 用户交互体验设计：考虑用户的操作习惯和需求，设计按钮、滑动条等交互控件，使得用户能够方便地进行操作和调整参数。

Matlab GUI设计快速傅里叶变换FFT程序的实例分析13. 以实际的信号分析为例，设计一个包括输入信号选择、窗函数选择、采样点数设置、FFT计算和结果展示等功能的GUI界面。

短时傅里叶变换 matlab程序短时傅里叶变换(Matlab程序)短时傅里叶变换（Short-Time Fourier Transform，STFT）是一种将信号从时域转换到频域的方法，它克服了傅里叶变换只能处理稳态信号的限制。

在实际应用中，我们经常需要对非稳态信号进行频谱分析，这时就可以使用短时傅里叶变换来获得信号的频谱信息。

在Matlab中，我们可以使用stft函数来实现短时傅里叶变换。

下面我们将介绍如何使用Matlab进行短时傅里叶变换，并给出一个简单的示例。

我们需要导入信号数据。

假设我们有一个包含音频信号的.wav文件，我们可以使用Matlab中的audioread函数将其读入到Matlab中。

假设读入的音频信号为x(n)，其中n为时间序列。

```matlab[x, fs] = audioread('audio.wav');```其中x为音频信号的时间序列，fs为采样率。

接下来，我们需要选择窗函数和窗长。

窗函数的作用是将信号分为若干个窗口，并对每个窗口进行傅里叶变换。

常用的窗函数有矩形窗、汉明窗等。

窗长的选择需要权衡频率与时间分辨率，一般选择合适的窗长可以获得较好的频谱分辨率。

在Matlab中，我们可以使用hamming函数生成汉明窗。

假设窗长为N，我们可以使用如下代码生成汉明窗：```matlabN = 256;window = hamming(N);```然后，我们可以调用stft函数进行短时傅里叶变换。

stft函数的输入参数包括信号序列x、窗函数window和窗长N。

该函数将返回短时傅里叶变换后的频谱。

```matlab[S, f, t] = stft(x, window, N);```其中S为频谱矩阵，f为频率向量，t为时间向量。

我们可以使用imagesc函数将频谱可视化。

imagesc函数将频谱矩阵作为输入，将其映射为彩色图像。

```matlabimagesc(t, f, abs(S));axis xy;colorbar;xlabel('时间');ylabel('频率');```上述代码将绘制出短时傅里叶变换后的频谱图像，横轴表示时间，纵轴表示频率。

傅里叶逆变换c程序傅里叶逆变换是一种将频域信号转化为时域信号的方法。

在数学中，它是一种将复数值函数从频域中恢复到时域中的方法。

以下是傅里叶逆变换的C程序示例。

```#include<stdio.h>#include<math.h>#define N 8 //N是信号长度，取2^n的形式void idft(double *x_r, double *x_i, double *y_r, double *y_i){int k,n;double sum_r,sum_i,w_r,w_i;for(k=0;k<N;k++) //计算Y[k]的实部和虚部{sum_r = 0;sum_i = 0;for(n=0;n<N;n++){w_r = cos(2*M_PI*k*n/N);w_i = -sin(2*M_PI*k*n/N);sum_r += x_r[n]*w_r - x_i[n]*w_i;sum_i += x_r[n]*w_i + x_i[n]*w_r;}y_r[k] = sum_r/N; //将结果保存到y_r和y_i中y_i[k] = sum_i/N;}}int main(){int k;double x_r[N]; //x_r和x_i是输入序列的实部和虚部double x_i[N];double y_r[N]; //y_r和y_i是输出序列的实部和虚部double y_i[N];printf("请输入实部：");for(k=0;k<N;k++)scanf("%lf",&x_r[k]);printf("请输入虚部：");for(k=0;k<N;k++)scanf("%lf",&x_i[k]);idft(x_r, x_i, y_r, y_i); //调用傅里叶逆变换函数printf("逆变换结果：\n");for(k=0;k<N;k++)printf("%f + %fi, ",y_r[k],y_i[k]);return 0;}```该程序使用了C语言中的复数类型来计算傅里叶逆变换结果。