上海大学物理化学B2 考前试卷讲解

大学物理2期末复习题第八章静电场一、选择题1、已知一高斯面所包围的体积内电量代数和∑Q i=0，则可肯定： C(A)高斯面上各点场强均为零。

(B)穿过高斯面上每一面元的电通量均为零。

(C)穿过整个高斯面的电通量为零。

(D)以上说法都不对。

2、关于高斯定理的理解有下面几种说法，其中正确的是： D(A)如果高斯面上 E 处处为零，则该面内必无电荷。

(B)如果高斯面内无电荷，则高斯面上 E 处处为零。

(C)如果高斯面上 E 处处不为零，则高斯面内必有电荷。

(D)如果高斯面内有净电荷，则通过高斯面的电通量必不为零。

(E)高斯定理仅适用于具有高度对称性的电场。

3、关于静电场中某点电势值的正负，下列说法中正确的是： C(A)电势值的正负取决于置于该点的试验电荷的正负。

(B)电势值正负取决于电场力对试验电荷作功的正负。

(C)电势值的正负取决于电势零点的选取。

(D)电势值的正负取决于产生电场的电荷的正负。

4、在已知静电场分布的条件下，任意两点P1和P2之间的电势差决定于 A（A）P1和P2两点的位置。

(B) P1和P2两点处的电场强度的大小和方向。

(C)试验电荷所带电荷的正负。

(D)试验电荷的电荷量。

二、填空题1、真空中电量分别为q1和q2的两个点电荷，当它们相距为r时，该电荷系统的相互作用电势能 W= ，(设当两个点电荷相距无穷远时电势能为零)。

q1q2/4πε0r2、一电子和一质子相距2×10-10 m(两者静止)，将此两粒子分开到无穷远距离时(两者仍静止)需要的最小能量是 eV 。

7.2(1/4πε0=9×109 N m2 /C2, 1eV=1.6 ×10-19J)3 电偶极矩大小p=4 2p /4πx3ε0是电偶极子在延长线上的电场5 取无限远为电势零点只能在电荷分布在有限区域时三、计算题：1、(5分) 一“无限长”均匀带电的空心圆柱体，内半径为a，外半径为b，电荷体密度为ρ，一半径为r(a ＜r ＜b)、长度为L 的同轴圆柱形高斯柱面，请计算其中包含的电量 解 ：q= V ρ (1) (2分)V=πl(r 2-a 2) (2) (2分)q=ρπl(r 2-a 2) (3) (1分)2 (5分)电量q 均匀分布在长为 2l 的细杆上，求在杆外延长线上与杆端距离为a 的p 点的电势( 设无穷远处为电势零点)。

物理化学B考试题及答案一、单项选择题（每题2分，共10分）1. 以下哪种物质的摩尔质量最大？A. 氢气（H2）B. 氧气（O2）C. 氮气（N2）D. 二氧化碳（CO2）答案：D2. 根据理想气体定律，当温度不变时，气体的压强与体积成什么关系？A. 正比B. 反比C. 无关D. 先正比后反比答案：B3. 热力学第一定律表明能量守恒，其表达式为：A. ΔU = Q + WB. ΔH = Q - WC. ΔG = Q + WD. ΔS = Q/T答案：A4. 以下哪种物质在室温下是液体？A. 氦气（He）B. 氮气（N2）C. 水（H2O）D. 二氧化碳（CO2）答案：C5. 根据范德华方程，实际气体与理想气体的主要区别在于：A. 分子间存在相互作用力B. 分子体积可以忽略不计C. 分子间没有相互作用力D. 分子体积不可忽略答案：A二、填空题（每题3分，共15分）1. 阿伏伽德罗常数的值约为 ________ mol^-1。

答案：6.022 x 10^232. 1摩尔理想气体在标准大气压下的体积为 ________ L。

答案：22.43. 热力学第二定律表明，不可能从单一热源吸热使之完全转化为功而不引起其他变化，这被称为 ________。

答案：开尔文表述4. 物质的三相点是指 ________、 ________ 和 ________ 共存的一个特定温度和压强。

答案：固态、液态、气态5. 根据吉布斯自由能的定义，当ΔG < 0时，反应是 ________。

答案：自发的三、简答题（每题10分，共20分）1. 简述熵的概念及其物理意义。

答案：熵是描述系统无序程度的物理量。

在热力学中，熵的增加表示系统从有序状态向无序状态的自发转变。

熵的物理意义在于它衡量了系统内部微观状态的多样性，以及系统与环境之间能量分布的均匀程度。

2. 什么是化学势？它在相平衡中的作用是什么？答案：化学势是描述在恒温恒压下，系统增加一个粒子时自由能变化的物理量。

XXXX 大学2011-2012-1学期《大学物理B2》本科期末考试试卷（B 卷）参考答案及评分细则一、选择题（每题3分,共30分） 1--10、ACADABEDCA 。

二、填空题（每题2分，共14分）1、02、0-I μ3、高4、]3π2π2cos[010/)t (.y P +-= 或 0.01cos t+ππ（2）35、arctan3-π或1arctan 23+π 6、2112/2+n e n λ或 2112/2-n e n λ 7、300三、计算题（共56分）1、（12分）解：长直导线在周围空间产生的磁场分布为B =μ0 I 1/(2πr )，取xoy 坐标如图所示，则在半圆线圈所在处产生的磁感应强度的大小为θR πI μB sin 210=（3分） 方向垂直纸面向里。

式中θ为场点至圆心的连线与y 轴的夹角。

半圆线圈上d l 段线电流所受的力为θr θR πI I μl B I I F d sin 2d d d 21022==⨯=B l （3分）根据对称性知 0=⎰y dF （2分）θF F x sin d d = 222102100II μππI I μdF F πx x =⋅==⎰方向垂直I 1向右。

（4分） 2、（12分）解 由于B 随时间变化，同时ab 导线切割磁场线，故回路中既存在感生电动势，又存在动生电动势。

t BS t S B t BS t Φd d d d d )(d d d +===ε )21(d d 21)21(d d 2t t lx lx t B += 势动εε+=. （6分）动ε的方向从b 指向a ，感ε的方向为逆时针方向。

oo xI将θθtan tan ,vt x l vt x ===代入上式，则 )21(d d tan 21)tan 21(d d 21222222t t t v t v t t i θθε+=θtan 32t v = （4分） i ε的方向为逆时针方向。

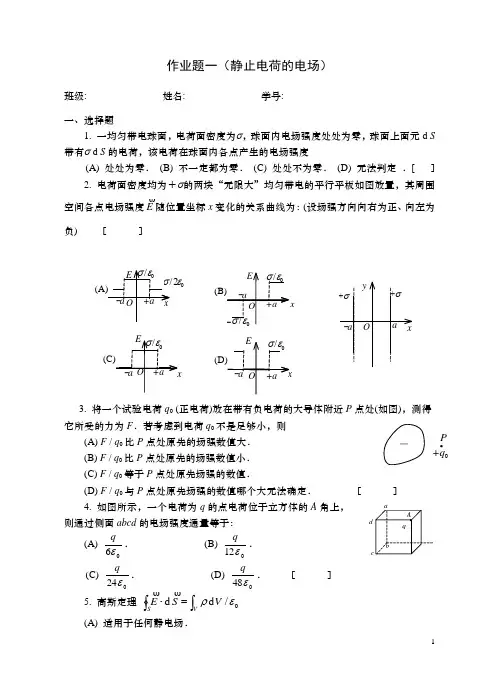
作业题一（静止电荷的电场）班级:_____________ 姓名:_____________ 学号:_____________ 一、选择题1. 一均匀带电球面，电荷面密度为σ，球面内电场强度处处为零，球面上面元d S 带有σ d S 的电荷，该电荷在球面内各点产生的电场强度(A) 处处为零． (B) 不一定都为零． (C) 处处不为零． (D) 无法判定 ．[ ］ 2. 电荷面密度均为＋σ的两块“无限大”均匀带电的平行平板如图放置，其周围空间各点电场强度E随位置坐标x 变化的关系曲线为：(设场强方向向右为正、向左为负) ［ ］3. 将一个试验电荷q 0 (正电荷)放在带有负电荷的大导体附近P 点处(如图)，测得它所受的力为F ．若考虑到电荷q 0不是足够小，则 (A) F / q 0比P 点处原先的场强数值大． (B) F / q 0比P 点处原先的场强数值小． (C) F / q 0等于P 点处原先场强的数值． (D) F / q 0与P 点处原先场强的数值哪个大无法确定． ［ ］4. 如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于：(A)06εq ． (B) 012εq． (C) 024εq ． (D) 048εq ． ［ ］5. 高斯定理 ⎰⎰⋅=VSV S E 0/d d ερ(A) 适用于任何静电场．02εxP +q 0(B) 只适用于真空中的静电场． (C) 只适用于具有球对称性、轴对称性和平面对称性的静电场．(D) 只适用于虽然不具有(C)中所述的对称性、但可以找到合适的高斯面的静电场． ［ ］6. 如图所示，两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电，沿轴线方向单位长度上所带电荷分别为λ1和λ2，则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小E 为：(A) r0212ελλπ+． (B) 20210122R R ελελπ+π(C) 1012R ελπ． (D) 0． ［ ］7. 点电荷Q 被曲面S 所包围 ， 从无穷远处引入另一点电荷q至曲面外一点，如图所示，则引入前后： (A) 曲面S 的电场强度通量不变，曲面上各点场强不变． (B) 曲面S 的电场强度通量变化，曲面上各点场强不变． (C) 曲面S 的电场强度通量变化，曲面上各点场强变化． (D) 曲面S 的电场强度通量不变，曲面上各点场强变化． ［ ］8. 根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中，正确的是：(A) 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零．(B) 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零． (C) 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零．(D) 闭合面上各点场强均为零时，闭合面内一定处处无电 ［ ］二、填空题9. A 、B 为真空中两个平行的“无限大”均匀带电平面，已知两平面间的电场强度大小为E 0，两平面外侧电场强度大小都为E 0/3，方向如图．则A 、B 两平面上的电荷面密度分别 为σA ＝_______________, σB ＝____________________．ABE 0E 0/3E 0/310. 三个平行的“无限大”均匀带电平面，其电荷面密度都是＋σ，如图所示，则A 、B 、C 、D 三个区域的电场强 度分别为：E A ＝_________________，E B ＝_____________， E C ＝_________，E D =___________ (设方向向右为正)．11. 一半径为R 的带有一缺口的细圆环，缺口长度为d (d<<R)环上均匀带有正电，电荷为q ，如图所 示．则圆心O 处的场强大小E ＝__________________ __________，场强方向为______________________．12. 如图所示，真空中两个正点电荷Q ，相距2R ．若以其中一点电荷所在处O 点为中心，以R 为半径作高斯球面S ，则通过该球面的电场强 度通量＝______________；若以 0r 表示高斯面外法线方向的单位矢量，则高斯面上a 、b 两点的电场强度分别为________________________． 三、计算题13. 带电细线弯成半径为R 的半圆形，电荷线密度为λ=λ0sin φ，式中λ0为一常数，φ为半径R 与x 轴所成的夹角，如图所示．试求环心O 处的电场强度．14. “无限长”均匀带电的半圆柱面，半径为R ，设半圆柱面沿轴线OO'单位长度上的电荷为λ，试求轴线上一点的电场强度．+σ+σ+σABCD15. 一半径为R的带电球体，其电荷体密度分布为 ρ =Ar(r≤R) ，ρ =0 (r＞R)A为一常量．试求球体内外的场强分布．16. 图中虚线所示为一立方形的高斯面，已知空间的场强分布为：Ex ＝bx，Ey＝0，Ez＝0．高斯面边长a＝0.1 m，常量b＝1000 N/(C·m)．试求该闭合面中包含的净电荷．(真空介电常数ε0＝8.85×10-12C2·N-1·m-2 ) x作业题二（电势）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. 在点电荷+q 的电场中，若取图中P 点处为电势零点 ， 则M 点的电势为 (A)a q 04επ． (B) a q 08επ． (C) a q 04επ-． (D) aq08επ-． ［ ］2. 如图所示，两个同心球壳．内球壳半径为R 1，均匀带有电荷Q ；外球壳半径为R 2，壳的厚度忽略，原先不带电，但与地相连接．设地为电势零点，则在内球壳里面，距离球心为r 处的P 点的场强大小及电势分别为： (A) E ＝0，U ＝104R Q επ． (B) E ＝0，U ＝⎪⎪⎭⎫ ⎝⎛-π21114R R Qε．(C) E ＝204r Q επ，U ＝r Q04επ (D) E ＝204r Q επ，U ＝104R Q επ．[ ] 3. 关于静电场中某点电势值的正负，下列说法中正确的是： (A) 电势值的正负取决于置于该点的试验电荷的正负． (B) 电势值的正负取决于电场力对试验电荷作功的正负． (C) 电势值的正负取决于电势零点的选取．(D) 电势值的正负取决于产生电场的电荷的正负． 4. 点电荷-q 位于圆心O 处，A 、B 、C 、D 为同一圆周上的四点，如图所示．现将一试验电荷从A 点分别移动到B 、C 、D 各点，则(A) 从A 到B ，电场力作功最大．(B) 从A 到C ，电场力作功最大． (C) 从A 到D ，电场力作功最大．(D) 从A 到各点，电场力作功相等． ［ ］ 5. 如图所示，直线MN 长为2l ，弧OCD 是以N 点为中心，l 为半径的半圆弧，N 点有正电荷＋q ，M 点有负电荷-q ．今将一试验电荷＋q 0从O 点出发沿路径OCDP 移到无穷远处，设无穷远处电势为零，则电场力作功A7.-(A) A ＜0 , 且为有限常量． (B) A ＞0 ,且为有限常量．(C) A ＝∞． (D) A ＝0． ［ ］ 6. 半径为r 的均匀带电球面1，带有电荷q ，其外有一同心的半径为R 的均匀带电球面2，带有电荷Q ，则此两球面之间的电势差U 1-U 2为： (A)⎪⎭⎫ ⎝⎛-πR r q 1140ε . (B) ⎪⎭⎫⎝⎛-πr R Q 1140ε .(C) ⎪⎭⎫ ⎝⎛-πR Q r q 041ε . (D)r q04επ . [ ] 7. 两块面积均为S 的金属平板A 和B 彼此平行放置，板间距离为d (d 远小于板的线度)，设A 板带有电荷q 1，B 板带有电荷q 2，则AB 两板间的电势差U AB 为(A) d S q q 0212ε+． (B) d Sq q 0214ε+．(C) d S q q 0212ε-． (D) d Sq q 0214ε-． ［ ］8. 面积为S 的空气平行板电容器，极板上分别带电量±q ，若不考虑边缘效应，则两极板间的相互作用力为(A)S q 02ε． (B) S q 022ε．(C) 2022S q ε． (D) 202Sq ε． ［ ］ 二、填空题9. 如图所示,两同心带电球面，内球面半径为r 1＝5 cm ，带电荷q 1＝3×10-8 C ；外球面半径为r 2＝20 cm ， 带电荷q 2＝－6×10­8C ，设无穷远处电势为零，则空间另一电势为 零的球面半径r ＝ __________________．10. 真空中一半径为R 的均匀带电球面，总电荷为Q ．今在球面上挖去很小一块面积△S (连同其上电荷)，若电荷分布不改变，则挖去小块后球心处电势(设无穷远处电势为零)为________________．11. 把一个均匀带有电荷+Q 的球形肥皂泡由半径r 1吹胀到r 2，则半径为R (r 1＜R ＜r 2)的球面上任一点的场强大小E 由______________变为______________；电 势U 由 __________________________变为________________(选无穷远处为电势零点)．12. 静电场的环路定理的数学表示式为：______________________．该式的物理意义是：____________________________________________________________．该定理表明，静电场是______ _________场．AS q 1q 2三、计算题13. 一“无限大”平面，中部有一半径为R的圆孔，设平面上均匀带电，电荷面密度为σ．如图所示，试求通过小孔中心O并与平面垂直的直线上各点的场强和电势(选O点的电势为零)．14. 图示为一个均匀带电的球层，其电荷体密度为ρ，球层内表面半径为R1，外表面半径为R2．设无穷远处为电势零点，求空腔内任一点的电势．15.两个带等量异号电荷的均匀带电同心球面，半径分别为R1＝0.03 m和R2＝0.10 m．已知两者的电势差为450 V，求内球面上所带的电荷．16. 有两根半径都是R的“无限长”直导线，彼此平行放置，两者轴线的距离是d (d≥2R)，沿轴线方向单位长度上分别带有＋λ和－λ的电荷，如图所示．设两带电导线之间的相互作用不影响它们的电荷分布，试求两导线间的电势差．作业题三（导体和电介质）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. A 、B 为两导体大平板，面积均为S ，平行放置，如图所示．A 板带电荷+Q 1，B 板带电荷+Q 2，如果使B 板接地，则AB 间电场强度的大小E 为 ［ ］(A) S Q 012ε ．(B) SQ Q 0212ε-．(C) SQ01ε． (D) S Q Q 0212ε+．2. 一带正电荷的物体M ，靠近一原不带电的金属导体N ，N 的左端感生出负电荷，右端感生出正电荷．若将N 的左端接地，如图所示，则(A) N 上有负电荷入地． (B) N 上有正电荷入地． (C ) N 上的电荷不动．(D) N 上所有电荷都入地． ［ ］ 3. 一导体球外充满相对介电常量为εr 的均匀电介质，若测得导体表面附近场强为E ，则导体球面上的自由电荷面密度σ为 ［ ］ (A) ε 0 E ． (B) ε 0 ε r E ． (C) ε r E ． (D) (ε 0 ε r - ε 0)E ．4. 一平行板电容器始终与端电压一定的电源相联．当电容器两极板间为真空时，电场强度为0E ，电位移为0D，而当两极板间充满相对介电常量为εr 的各向同性均匀电介质时，电场强度为E ，电位移为D，则 ［ ］(A) r E E ε/0 =，0D D =． (B) 0E E =，0D D rε=．(C) r E E ε/0 =，r D D ε/0 =． (D) 0E E =，0D D=．5. 在静电场中，作闭合曲面S ，若有0d =⎰⋅SS D (式中D为电位移矢量)，则S面内必定 ［ ］(A) 既无自由电荷，也无束缚电荷． (B) 没有自由电荷． (C) 自由电荷和束缚电荷的代数和为零．(D) 自由电荷的代数和为零．1+Q 2AB6. 一个大平行板电容器水平放置，两极板间的一半空间充有各向同性均匀电介质，另一半为空气，如图．当两极板带上恒定的等量异号电荷时，有一个质量为m 、带电荷为+q 的质点，在极板间的空气区域中处于平衡．此后，若把电介质抽去 ，则该质点 ［ ］(A) 保持不动． (B) 向上运动． (C) 向下运动． (D) 是否运动不能确定．7.一个平行板电容器，充电后与电源断开，当用绝缘手柄将电容器两极板间距离拉大，则两极板间的电势差U 12、电场强度的大小E 、电场能量W 将发生如下变化： ［ ］(A) U 12减小，E 减小，W 减小．(B) U 12增大，E 增大，W 增大． (C) U 12增大，E 不变，W 增大．(D) U 12减小，E 不变，W 不变． 8. 如图所示, 一球形导体，带有电荷q ，置于一任意形状的空腔导体中．当用导线将两者连接后，则与未连接前相比系统静电场能量将 (A) 增大． (B) 减小．(C) 不变． (D) 如何变化无法确定．［ ］ 二、填空题9. 半径为R 1和R 2的两个同轴金属圆筒，其间充满着相对介电常量为εr 的均匀介质．设两筒上单位长度带有的电荷分别为+λ和-λ，则介质中离轴线的距离为r 处的电位移矢量的大小D =____________，电场强度的大小 E =____________．10. 一平行板电容器，充电后与电源保持联接，然后使两极板间充满相对介电常量为εr 的各向同性均匀电介质，这时两极板上的电荷是原来的______倍；电场强度是原来的 _________倍；电场能量是原来的_________倍．11. 一平行板电容器，充电后切断电源，然后使两极板间充满相对介电常量为εr的各向同性均匀电介质．此时两极板间的电场强度是原来的____________倍；电场 能量是原来的___________ 倍．12. 分子的正负电荷中心重合的电介质叫做_______________ 电介质 ．在外电场作用下，分子的正负电荷中心发生相对位移，形成________________________．三、计算题13. 如图所示，一内半径为a 、外半径为b 的金属球壳，带有电荷Q ，在球壳空腔内距离球心r 处有一点电荷q ．设无限远处为电势零点，试求：(1) 球壳内外表面上的电荷． (2) 球心O 点处，由球壳内表面上电荷产生的电势．(3) 球心O 点处的总电势．+Q14. 半径分别为R1和R2 (R2 > R1 )的两个同心导体薄球壳，分别带有电荷Q1和Q2，今将内球壳用细导线与远处半径为r的导体球相联，如图所示, 导体球原来不带电，试求相联后导体球所带电荷q．1115. 假想从无限远处陆续移来微量电荷使一半径为R的导体球带电．(1) 当球上已带有电荷q时，再将一个电荷元d q从无限远处移到球上的过程中，外力作多少功？(2) 使球上电荷从零开始增加到Q的过程中，外力共作多少功？16. 一电容器由两个很长的同轴薄圆筒组成，内、外圆筒半径分别为R= 2 cm，R2 = 5 cm，其间充满相对介电常量为εr 的各1向同性、均匀电介质．电容器接在电压U = 32 V的电源上，(如图所示)，试求距离轴线R = 3.5 cm处的A点的电场强度和A点与外筒间的电势差．1213作业题四（电流的磁场）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. 如图，边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷．此正方形以角速度ω 绕AC 轴旋转时，在中心O 点产生的磁感强度大小为B 1；此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时，在O 点产生的磁感强度的大小为B 2，则B 1与B 2间的关系为 ［ ］(A) B 1 = B 2． (B) B 1 = 2B 2． (C) B 1 =21B 2． (D) B 1 = B 2 /4．2. 电流I 由长直导线1沿平行bc 边方向经a 点流入由电阻均匀的导线构成的正三角形线框，再由b 点沿垂直ac 边方向流出，经长直导线2返回电源(如图)．若载流直导线1、2和三角形框中的电流在框中心O 点产生的磁感强度分别用1B 、2B 和3B表示，则O 点的磁感强度大小(A) B = 0，因为B 1 = B 2 = B 3 = 0．(B) B = 0，因为虽然B 1≠ 0、B 2≠ 0，但021=+B B，B 3 = 0．(C) B ≠ 0，因为虽然B 2 = 0、B 3= 0，但B 1≠ 0．(D) B ≠ 0，因为虽然021≠+B B，但B 3≠ 0． ［ ］ 3. 通有电流I 的无限长直导线有如图三种形状，则P ，Q ，O 各点磁感强度的大小B P ，B Q ，B O 间的关系为：[ ](A) B P > B Q > B O . (B) B Q > B P > B O ．(C) B Q > B O > B P ． (D) B O > B Q > B P ．4. 边长为l 的正方形线圈，分别用图示两种方式通以电流I (其中ab 、cd 与正方形共面)，在这两种情况下，线圈在其中心产生的磁感强度的大小分别为： (A) 01=B ，02=B ．(B) 01=B ，lIB π=0222μ．(C) lIB π=0122μ，02=B ．C q3.a14 (D) l I B π=0122μ,lIB π=0222μ． ［ ］ 5. 如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知(A) 0d =⎰⋅Ll B，且环路上任意一点B = 0． (B) 0d =⎰⋅L l B，且环路上任意一点B ≠0． (C) 0d ≠⎰⋅Ll B，且环路上任意一点B ≠0．(D) 0d ≠⎰⋅Ll B，且环路上任意一点B =常量． ［ ］6. 如图，流出纸面的电流为2I ，流进纸面的电流为I ，则下述各式中哪一个是正确的？(A) I l H L 2d 1=⎰⋅． (B)I l H L =⎰⋅2d(C) I l H L -=⎰⋅3d． (D)I l H L -=⎰⋅4d． ［ ］7. 图中，六根无限长导线互相绝缘，通过电流均为I ，区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形，哪一个区域指向纸内的磁通量最大？ (A) Ⅰ区域． (B) Ⅱ区域． (C) Ⅲ区域． (D) Ⅳ区域． (E) 最大不止一个． ［ ］8. 如图两个半径为R 的相同的金属环在a 、b 两点接触(ab 连线为环直径)，并相互垂直放置．电流I 沿ab 连线方向由a 端流入，b 端流出，则环中心O 点的磁感强度的大小为 (A) 0． (B) RI40μ．(C) RI420μ． (D) R I 0μ． (E)RI820μ． ［ ］ 4ⅠⅡⅢⅣIIba15二、填空题9. 如图，在无限长直载流导线的右侧有面积为S 1和S 2的两个矩形回路．两个回路与长直载流导线在同一平面，且矩形回路的一边与长直载流导线平行．则通过面积为S 1的矩形回路的磁通量与通过面积为S 2的矩形回路的磁通量之比为____________． 10. 如图，平行的无限长直载流导线A 和B ，电流强度均为I ，垂直纸面向外，两根载流导线之间相距为a ，则(1) AB 中点(P 点)的磁感强度=p B_____________．(2) 磁感强度B沿图中环路L 的线积分=⎰⋅Ll Bd __________________________________．11. 图中所示的一无限长直圆筒，沿圆周方向上的面电流密度(单位垂直长度上流过的电流)为i ，则圆筒内部的磁感强度的大 小为B =________，方向_______________．12. 将半径为R 的无限长导体薄壁管(厚度忽略)沿轴向割去一宽度为h ( h << R )的无限长狭缝后，再沿轴向流有在管壁上均匀分布的电流，其面电流密度(垂直于电流的单位长度截线上的电流)为i (如上图)，则管轴线磁感强度的大小是__________________．三、计算题13. 半径为R 的无限长圆柱形导体和内半径为R 0，外半径也为R 的无限长圆筒形导体，都通有沿轴向的，在横截面上均匀分布的电流I ，导体的磁导率都为μ0．今取长为l 、宽为2 R 的矩形平面ABCD 和A ′B ′C ′D ′，AD 及A ′D ′正好在导体的轴线上，如图所示．(1) 通过ABCD 的磁通量大小为多少？(2) 通过A ′B ′C ′D ′的磁通量为多少？ (3) 若电流I 不变，外半径R 不变，圆筒壁变薄，直至壁厚趋于零，再求(2) ．10.l′ ′l16 14. 一根无限长导线弯成如图形状，设各线段都在同一平面内(纸面内)，其中第二段是半径为R 的四分之一圆弧，其余为直线．导线中通有电流I ，求图中O 点处的磁感强度．15. 平面闭合回路由半径为R 1及R 2 (R 1 > R 2 )的两个同心半圆弧和两个直导线段组成(如图)．已知两个直导线段在两半圆弧中心O 处的磁感强度为零，且闭合载流回路在O 处产生的总的磁感强度B 与半径为R 2的半圆弧在O 点产生的磁感强度B 2的关系为B = 2 B 2/3，求R 1与R 2的关系．16. 如图所示，一半径为R 的均匀带电无限长直圆筒，面电荷密度为σ．该筒以角速度ω绕其轴线匀速旋转．试求圆筒内部的磁感强度．R 1 R 2 OI17作业题五（电流在磁场中受力）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. 按玻尔的氢原子理论，电子在以质子为中心、半径为r 的圆形轨道上运动．如果把这样一个原子放在均匀的外磁场中，使电子轨道平面与B垂直，如图所示，则在r 不变的情况下，电子轨道运动的角速度将：［ ］(A) 增加． (B) 减小． (C)不变． (D)改变方向． 2. 如图，一个电荷为+q 、质量为m 的质点，以速度v沿x 轴射入磁感强度为B 的均匀磁场中，磁场方向垂直纸面向里，其范围从x = 0延伸到无限远，如果质点在x = 0和y = 0处进入磁场，则它将以速度v-从磁场中某一点出来，这点坐标是x = 0 和 ［ ］(A) qB m y v +=． (B) qB m y v2+=． (C) qB m y v 2-=． (D) qBm y v-=．3. 一铜条置于均匀磁场中，铜条中电子流的方向如图所示．试问下述哪一种情况将会发生？(A) 在铜条上a 、b 两点产生一小电势差，且U a > U b ． (B) 在铜条上a 、b 两点产生一小电势差，且U a < U b ． (C) 在铜条上产生涡流． (D) 电子受到洛伦兹力而减速． 4. 如图，无限长直载流导线与正三角形载流线圈在同一平面内，若长直导线固定不动，则载流三角形线圈将 ［ ］ (A) 向着长直导线平移． (B) 离开长直导线平移． (C) 转动． (D) 不动．5. 长直电流I 2与圆形电流I 1共面，并与其一直径相重合如图(但两者间绝缘)，设长直电流不动，则圆形电流将 (A) 绕I 2旋转． (B) 向左运动． (C) 向右运动． (D) 向上运动．(E) 不动． ［ ］I 11×××18 6. 如图，在一固定的载流大平板附近有一载流小线框能自由转动或平动．线框平面与大平板垂直．大平板的电流与线框中电流方向如图所示，则通电线框的运动情况对着从大平板看是： ［ ］(A) 靠近大平板． (B) 顺时针转动．(C) 逆时针转动． (D) 离开大平板向外运动．7. 两个同心圆线圈，大圆半径为R ，通有电流I 1；小圆半径为r ，通有电流I 2，方向如图．若r << R (大线圈在小线圈处产生的磁场近似为均匀磁场)，当它们处在同一平面内时小线圈所受磁力矩的大小为 ［ ］ (A)RrI I 22210πμ． (B)RrI I 22210μ．(C)rRI I 22210πμ． (D)0．8. 两根载流直导线相互正交放置，如图所示．I 1沿y 轴的正方向，I 2沿z 轴负方向．若载流I 1的导线不能动，载流I 2的导线可以自由运动，则载流I 2的导线开始运动的趋势是 [ ](A) 沿x 方向平动． (B) 绕x 轴转动． (C) 绕y 轴转动． (D) 无法判断． 二、填空题9. 如图，均匀磁场中放一均匀带正电荷的圆环，其线电荷密度为λ，圆环可绕通过环心O 与环面垂直的转轴旋转．当圆环 以角速度ω 转动时，圆环受到的磁力矩为_________________， 其方向__________________________．10. 有一半径为a ，流过稳恒电流为I 的1/4圆弧形载流导线bc ，按图示方式置于均匀外磁场B中，则该载流导线所受的安培力大小为_______________________．11. 如图所示，在真空中有一半径为a 的3/4圆弧形的导线，其中通以稳恒电流I ，导线置于均匀外磁场B 中，且B与导线所在平面垂直．则该载流导线bc 所受的磁力大小为_________________．12. 如图所示，在真空中有一半圆形闭合线圈，半径为a ，流过稳恒电流I ，则圆心O 处的电流元l I d 所受的安培力Fd 的大小为_______________，方向_________________．6.I 1I 2O r RI 1 I 2y zxI 1 I 2c aIIlI d19三、计算题13. 在一顶点为45°的扇形区域，有磁感强度为B方向垂直指向纸面内的均匀磁场，如图．今有一电子(质量为m ，电荷为-e )在底边距顶点O 为l 的地方，以垂直底边的速度 v射入该磁场区域，若要使电子不从上面边界跑出，电子的速度最大不应超过多少？14. 一圆线圈的半径为R ，载有电流I ，置于均匀外磁场B 中(如图示)．在不考虑载流圆线圈本身所激发的磁场的情况下，求线圈导线上的张力．(载流线圈的法线方向规定与B的方向相同．)l 45° vBO2015. 一矩形线圈边长分别为a =10 cm 和b =5 cm ，导线中电流为I = 2 A ，此线圈可绕它的一边OO ＇转动，如图．当加上正y 方向的B =0.5T 均匀外磁场B，且与线圈平面成30°角时，线圈的角加速度为β = 2rad/s 2，求∶(1) 线圈对OO ＇轴的转动惯量J =？(2) 线圈平面由初始位置转到与B 垂直时磁力所做的功？16. 一根同轴线由半径为R 1的长导线和套在它外面的内半径为R 2、外半径为R 3的同轴导体圆筒组成．中间充满磁导率为μ的各向同性均匀非铁磁绝缘材料，如图．传导电流I 沿导线向上流去，由圆筒向下流回，在它们的截面上电流都是均匀分布的．求同轴线内外的磁感强度大小B 的分布．O xyz I30° BO ′ ab作业题六（电磁感应）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. 将形状完全相同的铜环和木环静止放置，并使通过两环面的磁通量随时间的变化率相等，则不计自感时(A) 铜环中有感应电动势，木环中无感应电动势． (B) 铜环中感应电动势大，木环中感应电动势小． (C) 铜环中感应电动势小，木环中感应电动势大． (D) 两环中感应电动势相等． ［ ］2. 如图所示，矩形区域为均匀稳恒磁场，半圆形闭合导线回路在纸面内绕轴O 作逆时针方向匀角速转动，O 点是圆心且恰好落在磁场的边缘上，半圆形闭合导线完全在磁场外时开始计时．图(A)—(D)的 --t 函数图象中哪一条属于半圆形导线回路中产生的感应电动势？［ ］3. 一块铜板垂直于磁场方向放在磁感强度正在增大的磁场中时，铜板中出现的涡流(感应电流)将 (A) 加速铜板中磁场的增加． (B) 减缓铜板中磁场的增加．(C) 对磁场不起作用． (D) 使铜板中磁场反向． ［ ］4. 如图所示，导体棒AB 在均匀磁场B 中 绕通过C 点的垂直于棒长且沿磁场方向的轴OO ' 转动（角速度ω与B 同方向），BC 的长度为棒长的31，则 (A) A 点比B 点电势高．(B) A 点与B 点电势相等．(B) A 点比B 点电势低．(D)有稳恒电流从A 点流向B 点． [ ]☜t O (A)☜t O(C)☜ t O (B)☜ t O(D)5. 如图所示，直角三角形金属框架abc 放在均匀磁场中，磁场B平行于ab 边，bc 的长度为l ．当金属框架绕ab 边以匀角速度ω转动时，abc 回路中的感应电动势 和a 、c 两点间的电势差U a – U c 为 [ ](A) =0，U a – U c =221l B ω． (B) =0，U a – U c =221l B ω-． (C) =2l B ω，U a – U c =221l B ω．(D) =2l B ω，U a – U c =221l B ω-．6. 如图所示，两个线圈P 和Q 并联地接到一电动势恒定的电源上．线圈P 的自感和电阻分别是线圈Q 的两倍，线圈P 和Q 之间的互感可忽略不计．当达到稳定状态后，线圈P 的磁场能量与Q 的磁场能量的比值是［ ］(A) 4．(B) 2． (C) 1． (D) 21．7. 在感应电场中电磁感应定律可写成t l E LK d d d Φ-=⎰⋅ ，式中K E 为感应电场的电场强度．此式表明：(A) 闭合曲线L 上K E处处相等．(B) 感应电场是保守力场． (C) 感应电场的电场强度线不是闭合曲线． (D) 在感应电场中不能像对静电场那样引入电势的概念． ［ ］ 8. 对位移电流，有下述四种说法，请指出哪一种说法正确． (A) 位移电流是指变化电场． (B) 位移电流是由线性变化磁场产生的． (C) 位移电流的热效应服从焦耳─楞次定律． (D) 位移电流的磁效应不服从安培环路定理． ［ ］二、填空题9. 如图所示，aOc 为一折成∠形的金属导线(aO =Oc =L )，位于xy 平面中,磁感强度为 B的匀强磁场垂直于xy 平面．当aOc 以速度v沿x 轴正向运动时，导线上a 、c 两点间电势差U ac =____________；当aOc 以速度v沿y 轴正向运动时，a 、c 两点的电势相比较, 是____________点电势高．Bab clωx ×××××10. 一导线被弯成如图所示形状，acb 为半径为R 的四分之三圆弧，直线段Oa 长为R ．若此导线放在匀强磁场B 中，B的方向垂直图面向内．导线以角速度ω在图面内绕O 点匀速转动，则此导线中的动生电动势 i =___________ ， 电势最高的点是________________________．11. 一长直导线旁有一长为b ，宽为a 的矩形线圈，线圈与导线共面，长度为b 的边与导线平行且与直导线相距为d ，如图．线圈与导线的互感系数为 ______________________．12. 一无铁芯的长直螺线管，在保持其半径和总匝数不变的情况下，把螺线管拉长一些，则它的自感系数将____________________．三、计算题13. 均匀磁场 B被限制在半径R =10 cm 的无限长圆柱空间内，方向垂直纸面向里．取一固定的等腰梯形回路abcd ，梯形所在平面的法向与圆柱空间的轴平行，位置如图所示．设磁感强度以d B /d t =1 T/s 的匀速率增加，已知 π=31θ，cm 6==Ob Oa ，求等腰梯形回路中感生电动势的大小和方向．14.如图所示，有一半径为r =10 cm 的多匝圆形线圈，匝数N =100，置于均匀磁场B中(B = 0.5 T )．圆形线圈可绕通过圆心的轴O 1O 2转动，转速 n =600 rev/min ．求圆线圈自图示的初始位置转过π21时，(1) 线圈中的瞬时电流值(线圈的电阻R 为 100 Ω，不计自感)；(2) 圆心处的磁感强度．(μ0 =4π×10-7 H/m)c15. 两个半径分别为R和r的同轴圆形线圈相距x，且R>>r，x >>R．若大线圈通有电流I而小线圈沿x轴方向以速率v运动，试求x =NR时(N为正数)小线圈回路中产生的感应电动势的大小．16. 载有电流的I长直导线附近，放一导体半圆环MeN与长直导线共面，且端点MN的连线与长直导线垂直．半圆环的半径为b，环心O与导线相距a．设半圆环以速度v 平行导线平移，求半圆环内感应电动势的大小和方向以及MN两端的电压UMU N ．。

大学物理b试题库及答案详解大学物理B试题库及答案详解在大学物理B的课程学习中，学生往往需要通过大量的练习来加深对物理概念的理解和应用能力。

本文将提供一套大学物理B试题库及答案详解，以帮助学生更好地掌握物理知识。

一、选择题1. 某物体的质量为2kg，受到的重力大小为多少牛顿？A. 19.6 NB. 20 NC. 20.4 ND. 21 N答案：B解析：根据重力公式 \( F = mg \)，其中 \( m \) 为物体的质量，\( g \) 为重力加速度（取9.8 m/s²），计算得 \( F = 2 \times 9.8 = 19.6 \) N。

由于选项中没有19.6 N，故选择最接近的20 N。

2. 光在真空中的传播速度是多少？A. 299792 km/sB. 299792.458 km/sC. 300000 km/sD. 299792.5 km/s答案：B解析：光在真空中的传播速度精确值为 \( 299792.458 \) km/s。

二、填空题1. 牛顿第二定律的表达式为 ________ 。

2. 根据能量守恒定律，一个物体的动能与其势能之和在没有外力作用下保持不变，这被称为________。

答案：1. \( F = ma \)2. 机械能守恒定律解析：1. 牛顿第二定律描述了力与加速度之间的关系，即 \( F = ma \)，其中 \( F \) 是作用在物体上的力，\( m \) 是物体的质量，\( a \) 是物体的加速度。

2. 机械能守恒定律是能量守恒定律在宏观物体运动中的应用，它指出在没有外力作用的情况下，一个系统的总机械能（动能加势能）是守恒的。

三、简答题1. 简述什么是电磁感应现象，并给出一个应用实例。

答案：电磁感应现象是指当导体在变化的磁场中移动时，导体中会产生感应电动势和感应电流的现象。

这一现象是由法拉第电磁感应定律所描述的。

一个常见的应用实例是发电机，它利用电磁感应原理将机械能转换为电能。

大学化学专业《大学物理（二）》期末考试试题B卷附解析姓名：______ 班级：______ 学号：______考试须知：1、考试时间：120分钟，本卷满分为100分。

2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。

一、填空题（共10小题，每题2分，共20分）1、将热量Q传给一定量的理想气体：（1）若气体的体积不变，则热量转化为_____________________________。

（2）若气体的温度不变，则热量转化为_____________________________。

（3）若气体的压强不变，则热量转化为_____________________________。

2、长为的匀质细杆，可绕过其端点的水平轴在竖直平面内自由转动。

如果将细杆置与水平位置，然后让其由静止开始自由下摆，则开始转动的瞬间，细杆的角加速度为_____，细杆转动到竖直位置时角加速度为_____。

3、从统计的意义来解释, 不可逆过程实质上是一个________________的转变过程, 一切实际过程都向着________________ 的方向进行。

4、一质点作半径为0.1m的圆周运动，其运动方程为：（SI），则其切向加速度为＝_____________。

5、一弹簧振子系统具有1.OJ的振动能量，0.10m的振幅和1.0m／s的最大速率，则弹簧的倔强系数为_______，振子的振动频率为_______。

6、均匀细棒质量为，长度为，则对于通过棒的一端与棒垂直的轴的转动惯量为_____，对于通过棒的中点与棒垂直的轴的转动惯量_____。

7、一束平行单色光垂直入射在一光栅上，若光栅的透明缝宽度与不透明部分宽度相等，则可能看到的衍射光谱的级次为____________。

8、长为、质量为的均质杆可绕通过杆一端的水平光滑固定轴转动，转动惯量为，开始时杆竖直下垂，如图所示。

现有一质量为的子弹以水平速度射入杆上点，并嵌在杆中. ，则子弹射入后瞬间杆的角速度___________。

名姓2010 —2011学年第1 学期《物理化学B》课程考试试卷（A卷）注意：1、本试卷共 4 页；2、考试时间：120分钟题号■---一二二二四五六总分阅卷人得分3、姓名、学号必须写在指定地方4、专业：09级食科和农资专业、选择题（每小题2分，共24 分）1.关于循环过程，下列表述正确的是（A.可逆过程一定是循环过程C.循环过程Q 0）。

B.循环过程不一定是可逆过程D.对理想气体：：C V dT 02.下述化学势的公式中，不正确的是（）。

号学G H AA. B. C.Dn B T,p,n c n B n B S, p,n C n Bn BBT,p,n nUnB S,V ,nCnB级班3. 在相图上，当系统处于下列哪一点时，只存在一个相（）。

A.恒沸点B.熔点C.临界点D.低共熔点4. 单原子分子理想气体的C V, m =-R，温度由T1变到T2时，等压过程系统的熵变2A S p与等容过程熵变 0 之比是（）。

A. 1 : 1B. 2 : 1C. 3 : 5D. 5 : 35. 298 K，当H2SO4溶液的浓度从0.01 mol kg-1增加到0.1 mol kg-1时，其电导率k和摩尔电导率m将（）。

院学卷试学大江长A . k减小，m增加C. k减小，m减小6.对化学反应进度E,下列表述正确的是（B. k增加，m增加D. k增加，m减小）。

A. E值与反应式的写法无关B. E值是体系的状态函数，其值不小于零C. 对指定的反应，E值与物质的选择有关D. 对指定的反应，随反应的进行E值不变7.某电池反应为2 Hg （l）+ O2 （g） + 2 H2O （l）= 2 Hg2++ 4OH -，当电池反应达平衡时，电池的电动势E必然是（）。

A. E >0B. E =EC. E <0D. E =08. 下列系统中为非胶体的是（）。

A.泡沫B.珍珠C.云雾D.空气9. 光气热分解的总反应为COCI2T CO + Cl2，该反应分为三步完成：（1）COCI2 ' 2CI + CO 快速可逆（2）CI + COCI 2 T CO +CI2 慢（3）CI3 'CI2+CI 快速可逆一 d C COCI1总反应速率方程------- 2kC cOg C Cs，则此总反应为（）。

大学物理b2试题及答案根据题目要求，以下是一篇符合要求的大学物理B2试题及答案内容：一、选择题（每题2分，共20分）1. 一个物体从静止开始做匀加速直线运动，第1秒内、第2秒内、第3秒内位移之比为：A. 1:3:5B. 1:2:3C. 1:3:6D. 1:4:9答案：B2. 一质点做匀速圆周运动，其角速度为ω，周期为T，则其线速度大小为：A. ωTB. 2πωC. 2π/TD. ω/2π答案：C3. 一弹簧振子做简谐振动，振幅为A，周期为T，其最大加速度为：A. 2πA/TB. 4π²A/TC. 2A/TD. 4A/T²答案：B4. 一物体从高度为h处自由下落，不计空气阻力，其落地时的速度大小为：A. √(2gh)B. √(gh)C. √(2h/g)D. √(h/g)答案：A5. 一物体以初速度v₀沿斜面匀加速下滑，加速度大小为a，斜面倾角为θ，则其沿斜面下滑的加速度大小为：A. aB. a*sinθC. a*cosθD. a*tanθ答案：B6. 一质量为m的物体以初速度v₀沿水平方向抛出，忽略空气阻力，其落地时的速度大小为：A. v₀B. √(v₀²+2gh)C. √(v₀²+2gh)*sinθD. √(v₀²+2gh)*cosθ答案：B7. 一质量为m的物体以初速度v₀沿斜面匀加速上滑，加速度大小为a，斜面倾角为θ，则其沿斜面上升的加速度大小为：A. aB. a*sinθC. a*cosθD. a*tanθ答案：C8. 一质量为m的物体从高度为h处自由下落，不计空气阻力，其落地时的动能为：A. mghB. 1/2mv₀²C. 1/2mv²D. 1/2mv₀²+mgh答案：C9. 一质量为m的物体以初速度v₀沿水平方向抛出，忽略空气阻力，其落地时的动能为：A. 1/2mv₀²B. 1/2mv²C. 1/2mv₀²+mghD. 1/2mv²+mgh答案：D10. 一质量为m的物体从高度为h处自由下落，不计空气阻力，其落地时的重力势能变化量为：A. -mghB. mghC. 0D. 2mgh答案：A二、填空题（每题2分，共20分）11. 一物体做匀加速直线运动，初速度为v₀，加速度为a，第t秒内的位移为x，则x=v₀t+1/2at²。

物化B 卷参考答案及评分标准参考答案一．选择题1.A2.C3.A4.D5.B6.D7.C8.B9.B 10.C11.B 12.C 13.A 14.B 15.A 16.C 17.B 18.A 19.A 20.C二．填空题1.CO 2（g ）；2.气液相不分3.Φ = 2，C = 14.<5.0.3976.C V /C p7.<8.吉布斯函数9.例如：节流膨胀，理想气体恒温变化三．解：(1)A 1000K T =,3A 0.001m V =A A AnRT p V =1131mol 8.314J mol K 1000K 0.001m --⨯⋅⋅⨯=8314kPa = (1分) B 态：因为A 到B 为等温可逆过程，所以,B A 1000K T T ==，3B 0.020m V =,则BB B1131mol 8.314J mol K 1000K 0.020m415.7kPanRT p V --=⨯⋅⋅⨯== (1分)C 态：B 到C 为等容过程，故3C B 0.020m V V ==。

因为C 到A 为绝热可逆过程，所以11C C A A T V T V γγ--=对双原子理想气体,m ,m 72 1.452p V RC C R γ=== 11A C A C 11000K 301.7K 20V T T V γ-1.4-⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭(2分) CC C1131mol 8.314J mol K K 0.020m 125.4kPanRT p V --=⨯⋅⋅⨯301.7== (1分)(2)A 到B 为等温可逆过程，由于理想气体的热力学能和焓仅是温度的函数，所以ΔU 1=0， ΔH 1=0B11A11ln 201mol 8.314J mol K K ln124.91kJV Q W nRT V --=-==⨯⋅⋅⨯1000⨯= (2分)B 到C 为等容过程，所以()()CB 2C B 115d 21mol 8.314J mol K K kJ T V V T U Q C T n R T T --∆===-5=⨯⨯⋅⋅⨯301.7-1000K 2=-14.51⎰ (2分)()()CB 2C B 117d 21mol 8.314J mol K 3017K 2032kJ T p T H C T n R T T --∆==-7=⨯⨯⋅⋅⨯.-1000K 2=-.⎰ (2分)C 到A 为绝热可逆过程，所以Q 3=0()()()33A C A C 115=21mol 8.314J mol K 1000K 14.51kJV U W C T T n R T T --∆=-=-5=⨯⨯⋅⋅⨯-301.7K 2=(2分)()()A C 3A C 117d 21mol 8.314J mol K 1000K 2032kJT p T H C T n R T T --∆==-7=⨯⨯⋅⋅⨯-301.7K 2=.⎰ (2分)也可利用循环积分为零原则计算ΔU 3，ΔH 3 (3)()123124.91014.51kJ 100%41.75%24.91kJ W W W W Q Q η+-----===⨯=吸(2分)()A h 1C h A 1000301.7100%69.83%1000C T T T T T T K K η--==-=⨯=(2分)C 41.75%0.597969.83%ηη== (1分)四．解:以10g 水和1g 冰为系统，设热量不传递到环境，并设终态温度为T()()fus m ,m ,m 273.2K 373.2K p p n H n C T n C T ∆+-=-冰冰水 (3分)()()11111111mol J mol mol J mol K 273.2mol 7531J mol K 373.2181818T T -----⨯6025⋅+⨯75.31⋅⋅⨯-K =⨯.⋅⋅⨯K -(3分)356.8K T =(2分)0Q =(1分)0W p V =-∆≈(1分)0U Q W ∆=+=(1分)0H U p V ∆=∆+∆=(1分)123S S S S ∆=∆+∆+∆(1分)f b ,m ,m fus m f d d T T p p T T n C n C n H T T T T T ∆=++⎰⎰冰水冰(4分)111111mol J mol 1356.8K 10356.8K 18mol J mol K ln mol J mol K ln 273.2K 18273.2K 18373.2K-----⨯6025⋅=+⨯75.31⋅⋅⨯+⨯75.31⋅⋅⨯10.4618J K -=⋅ (3分)五．解：（1）11B 2.22g111.0g mol 0.02mol kg 1kgb --⋅==⋅(2分) 11b b B 0.52K mol kg 0.02mol kg 0.01K T K b --∆==⋅⋅⨯⋅=(2分)(2)1B B 0.02mol kg 1kg dm 0.02mol dm c b ρ--3-3≈⨯=⋅⨯⋅=⋅(2分)11B 0.02mol m 8.314J mol K kPa c RT ∏-3--==⨯1000⋅⨯⋅⋅⨯298.15K =49.58(2分)(3)已知373.15K 时水的饱和蒸汽压101325kPa ，由克克方程求解()vap m 21212H O 11ln H p p R T T ∆⎛⎫=-- ⎪⎝⎭(2分)111140670J mol 1ln 101325Pa 8.314J mol K K 373.15K p -----⋅1⎛⎫=⨯ ⎪⋅⋅298.15⎝⎭(2分) 13747Pa p =(1分)A A AB 1000mol 180.99961000 2.22mol+mol 18100n x n n ===+ A 1A 3747Pa 0.9996=3745Pa p p x ==⨯(2分)六． （1）各相区的稳定相：相区1：l +C(s)；相区2：l +D(s)；相区3：l +β(固溶体)；相区4：β；相区5：D(s)+β(5分)（2）各三相线上的相平衡：ac 线上：l (E 1)A(s) + C(s) (2分) dE2线上：C(s) + l (E 2)D(s) (2分) mn 线上：l (E 3)D(s) + β (2分)（3）通过图中系统点x, y 两条冷却曲线的形状及冷却过程的相变化如图所示。

1 一个半径为R 的均匀带点球面，电量为Q ，若规定该球面上电势值为零，则无限远处电势多少？解：带电球面在外部产生的场强为204Q Er πε=，由于 d d RRRU U E r ∞∞∞-=⋅=⎰⎰E l200d 44RRQQr r r πεπε∞∞-==⎰ 04Q Rπε=当U R = 0时，04Q U Rπε∞=-2 均匀带点球壳内半径为6cm ，外半径为10cm ，电荷体密度为2×10-5，求距球心为5cm ，8cm 及12cm 各点的场强。

解: 高斯定理0d ε∑⎰=⋅q S E s,02π4ε∑=qrE当5=r cm 时，0=∑q ,0=E8=r cm 时，∑q 3π4p=3(r )3内r - ∴ ()2023π43π4r r r E ερ内-=41048.3⨯≈1C N -⋅，方向沿半径向外．12=r cm 时,3π4∑=ρq -3(外r ）内3r ∴ ()420331010.4π43π4⨯≈-=r r r E ερ内外 1CN -⋅沿半径向外.3两条长直载流导线与一长方形线圈共面，如图，已知a=b=c=10，I=10m，I1=I2=100A，求通过线圈的磁通量。

4把折射率n=1.632的玻璃片，放入到麦克斯韦干涉仪的一臂上，可观察到150条干涉条纹向一方移动，若所用的单色光波长为=5000A，求玻璃片的厚度。

5使一束自然光通过两个偏振化方向成60°角的偏振片后，透射光的强度为I1，今在两个偏振之间再插入另一个偏振片，使它的偏振化方向与原来两个偏振片的偏振化方向的夹角均成30°，求此时透射光的强度为多大？6某单色光垂直入射到每厘米刻有6000多条刻线的光栅上，如果第一级谱线的偏角为20°，试问入射光的波长如何？它的第二级谱线在何处？（sin20°=0.342）7三块平行金属板A、B和C，面积都是S，A、B相距d1，A、C相距d2，d1:d2=1:2，B、C接地，A带正电荷q，忽略边缘效应，求（1）B、C板上的电荷多少？1（2）A板电势为多少？（素材和资料部分来自网络，供参考。