当前位置：文档之家 › 第1章气体的PVT关系

第1章气体的PVT关系

  • 格式：ppt
  • 大小：2.45 MB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

物理化学(天津大学第五版)课后答案

物理化学(天津大学第五版)课后答案

物理化学上册习题解（天津大学第五版）第一章 气体的 pVT 关系1-1 物质的体膨胀系数 V与等温压缩系数 T 的定义如下：1 V 1 VV TV T p试导出理想气体的V、T与压力、温度的关系？解：对于理想气体，pV=nRTV p T1 V VT V 1 V Tp VpT1 (nRT / p)V T1 ( nRT / p) Vp1 nR 1 V T 1 p V p V T 1 nRT 1 V p 1T V p 2 V p1-2 气柜内有 3 90kg 的流量输往使用车间，试问贮121.6kPa 、27℃的氯乙烯（ C2H3Cl ）气体 300m ，若以每小时 存的气体能用多少小时？解：设氯乙烯为理想气体，气柜内氯乙烯的物质的量为pV121.6 103300n 8.314 14618.623molRT 300.15 3 3 每小时 90kg 的流量折合 p 摩尔数为 v90 10 90 10 1441.153mol h 1M C 2H3Cl 62.45 n/v= （ 14618.623 ÷1441.153 ） =10.144 小时1-3 0 ℃、 101.325kPa 的条件常称为气体的标准状况。

试求甲烷在标准状况下的密度。

解：CH 4 n M CH 4 p M CH 4 101325 16 103 0.714kg m 3V RT 8.314 273.151-4 一抽成真空的球形容器，质量为 25.0000g 。

充以 4℃水之后，总质量为 125.0000g 。

若改用充以 25℃、 13.33kPa 的某碳氢化合物气体，则总质量为 25.0163g 。

试估算该气体的摩尔质量。

解：先求容器的容积V125.0000 25.000 100.0000 cm 3 100.0000cm 3H 2 O(l ) 1n=m/M=pV/RTM RTm 8.314 298.15 (25.0163 25.0000) mol pV 13330 10 430.31g1-5 两个体积均为 V 的玻璃球泡之间用细管连接，泡内密封着标准状况条件下的空气。

第一章气体的PVT关系

第一章气体的PVT关系


§1.2 理想气体混合物
1. 混合物的组成
（1）摩尔分数x或y
xB(或yB) nB nA
A
本书中气体混合物的摩尔分数一般用 y 表示，液体混合物的摩 尔分数一般用 x 表示。
（2）质量分数 ω B
ωB mB
mA
A
(3) 体积分数 B
B
xBVm*B, (
xAVm*A, )
V
* m,
A
A
：一定压力、温度下纯物质A的摩尔体积。
临界温度下的饱和蒸汽压为临界压力，pc 是在临界温度下使气体液化做需要的
最低压力
临界摩尔体积Vm,c：在Tc, pc下物质的摩尔体积
Tc, pc , Vm,c：临界参数
§1.3 气体的液化及临界参数
液体的饱和蒸汽压 临界参数
真实气体的p-Vm图及气体的液化
3.真实气体的p-Vm图及气体的液化
等温线的三种类型： T>Tc(不可液化) T<Tc(加压可液化) T=Tc
V VB*
B
VnR /p T ( nB)R/T p
B
(nB p R)T BV B *
VB* nBRT/ p
理想气体混合物中物质B的分体积等于纯气体B在混合 物温度及总压条件下所占有的体积。
理想气体混合物的体积具有一定的加和性。在相同 的温度和压力下，混合后的总体积等于混合前各组 分的体积之和。
由pVT数据拟合得到Z~p关系.
3. 对应状态原理
对比参数反映了气体所处状态偏离临界点 的倍数。 各种不同气体，只要两个对比参数相同， 第三个参数必相同，这就是对应状态原理。 此时的气体处于相同的对应状态。
3. 普遍化压缩因子图
将对比状态参数的表达式引入到压缩因子 定义式中，得到：
天津大学_第五版_物理化学上习题答案

天津大学_第五版_物理化学上习题答案

第一章 气体的pVT 关系1-1物质的体膨胀系数V α与等温压缩系数T κ的定义如下：1 1TT p V p V V T V V ⎪⎪⎭⎫⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂=κα 试导出理想气体的V α、T κ与压力、温度的关系？解：对于理想气体，pV=nRT111 )/(11-=⋅=⋅=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=T TVV p nR V T p nRT V T V V p p V α 1211 )/(11-=⋅=⋅=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-=p p V V pnRT V p p nRT V p V V T T T κ 1-2 气柜内有121.6kPa 、27℃的氯乙烯（C 2H 3Cl ）气体300m 3，若以每小时90kg 的流量输往使用车间，试问贮存的气体能用多少小时？解：设氯乙烯为理想气体，气柜内氯乙烯的物质的量为mol RT pV n 623.1461815.300314.8300106.1213=⨯⨯⨯==每小时90kg 的流量折合p 摩尔数为 133153.144145.621090109032-⋅=⨯=⨯=h mol M v Cl H Cn/v=（14618.623÷1441.153）=10.144小时1-3 0℃、101.325kPa 的条件常称为气体的标准状况。

试求甲烷在标准状况下的密度。

解：33714.015.273314.81016101325444--⋅=⨯⨯⨯=⋅=⋅=m kg M RT p M V n CH CH CH ρ 1-4 一抽成真空的球形容器，质量为25.0000g 。

充以4℃水之后，总质量为125.0000g 。

若改用充以25℃、13.33kPa 的某碳氢化合物气体，则总质量为25.0163g 。

试估算该气体的摩尔质量。

解：先求容器的容积33)(0000.10010000.100000.250000.1252cm cm V l O H ==-=ρn=m/M=pV/RTmol g pV RTm M ⋅=⨯-⨯⨯==-31.301013330)0000.250163.25(15.298314.841-5 两个体积均为V 的玻璃球泡之间用细管连接，泡内密封着标准状况条件下的空气。

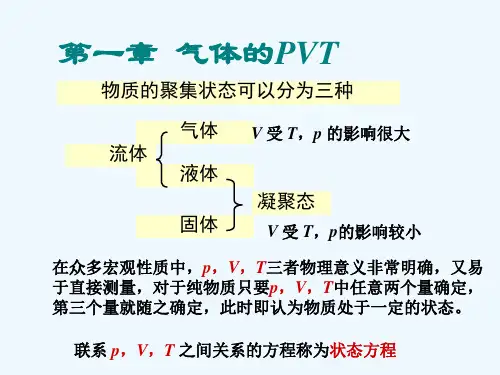
第一章气体的pVT关系PPT资料29页

第一章气体的pVT关系PPT资料29页


上一内容 下一内容 回主目录
返回
2020/6/20
§1.2 理想气体混合物
解：
yO2
nO2 n
pVO2 RT
VO2
pV V
O2
0.29
RT
pO 2yO 2p29.3 28 5 P4a
VO 2 O2V0.29m 3
上一内容 下一内容 回主目录
返回
2020/6/20
§1.2 理想气体混合物
nnO2 1 mo3 l.49mol yO2 0.29
VnpRT 3.4 98.311 05 217 .3 13 2 5255 m 3
0.08m 53
上一内容 下一内容 回主目录
返回
2020/6/20
§1.3 气体的液化及临界参数
1. 液体的饱和蒸气压 液体蒸发的速度和气体凝结的速度相
等时的蒸气压力。
P＝P饱和
P＜P饱和
P＞P饱和
上一内容 下一内容 回主目录
上一内容 下一内容 回主目录
返回
2020/6/20
§1.1 理想气体的状态方程
2.理想气体的模型
• 真实气体微观模型：分子间有相互作用，分子 本身有体积。
E0
不 可
0
无
0
限
r
压
缩
分子势能曲线
上一内容 下一内容 回主目录
返回
2020/6/20
§1.1 理想气体的状态方程
•理想气体微观模型：分子间无相互作用， 分子本身无体积。
3.道尔顿分压定律
pB = yB p = (nB/n)p = (nB/n) nRT/V 所以 pB=nBRT/V
pB yBpp
B
B
01气体的pVT关系

01气体的pVT关系


临界温度以上不再有液体存在，
p*=f (T) 曲线终止于临界温度； 临界温度 Tc 时的饱和蒸气压称为临界压力。
临界压力:（critical pressure ，pc）在临界温度下时
的饱和蒸气压。是在临界温度下使气体液化所需要 的最低压力。 临界摩尔体积:（critical molar volume，Vm,c）是在 临界温度和临界压力下物质的摩尔体积。 临界状态：物质处于临界温度、临界压力下的状态。
拐点C； S 型曲线两端有过饱和蒸气和 过热液体的含义。
图1.3.2 真实气体p-Vm等温线示意图
26
用范德华方程计算，在已知T , p，求Vm时，需解一元三次方程
T > Tc 时，Vm有 一个实根，两个虚根，虚根无意义； T = Tc时， 如 p = pc ：Vm 有三个相等的实根； 如 p pc ： 有一个实根，二个虚根，
对于任何气体混合物，分压为
pB yB p
对于理想气体混合物
p pB
B
pB nB RT / V
适用范围：理想气体混合物和低压下的真实气体混合物。
即理想混合气体的总压等于各组分单独存在于混合气体的T、 V 条件下所产生的压力总和 道尔顿分压定律
4.阿马加分体积定律（Amagat’s law of partial volume）
整理可得如下状态方程:
单位：p Pa TK
pV nRT 或 pVm RT 或 pV m M RT
V m3 n mol R J mol-1 K-1

2.理想气体(perfect gas)模型
吸引力 分子相距较远时，有范德华引力；
排斥力 分子相距较近时，电子云及核产生排斥作用。
7-32第一章 气体的pVT关系

7-32第一章 气体的pVT关系

第一章 气体的pVT 关系物质的聚集状态一般可分为三种，即气体、液体和固体。

气体与液体均可流动，统称为流体；液体和固体又统称为凝聚态。

三种状态中，固体虽然结构较复杂，但粒子排步的规律性较强，对它的研究已有了较大的进展；液体的结构最复杂，人们对其认识还很不充分；气体则最为简单，最容易用分子模型进行研究，故对它的研究最多，也最为透彻。

无论物质处于哪一种聚集状态，都有许多宏观性质，如压力p ，体积V ，温度T ，密度ρ，热力学能U 等等。

众多宏观性质中，p , V , T 三者是物理意义非常明确、又易于直接测量的基本性质。

对于一定量的纯物质，只要p , V , T 中任意两个量确定后，第三个量即随之确定，此时就说物质处于一定的状态。

处于一定状态的物质，各种宏观性质都有确定的值和确定的关系①。

联系p , V , T 之间关系的方程称为状态方程。

状态方程的建立常成为研究物质其它性质的基础。

液体和固体两种凝态，其体积随压力和温度的变化均较小，即等温压缩率T T p V V ⎪⎪⎭⎫ ⎝⎛∂∂-=1κ和体膨胀系数pV T V V ⎪⎭⎫ ⎝⎛∂∂=1α都较小，故在通常的物理化学计算中常忽略其体积随压力和温度的变化。

与凝聚态相比，气体具有较大的等温压缩率κT 和体膨胀系数αV ，在改变压力和温度时，体积变化较大。

因此一般的物理化学中只讨论气体的状态方程。

根据讨论的p , T 范围及使用精度的要求，通常把气体分为理想气体和真实气体分别讨论。

§1.1 理想气体状态方程1.理想气体状态方程从17世纪中期，人们开始研究低压下（p <1 MPa ）气体的p VT 关系发现了三个对各种气体均适用的经验定律：（1）波义尔(Boyle R)定律 在物质的量和温度恒定的条件下，气体的体积与压力成反比，即p V =常数 （n ,T 一定）（2）盖－吕萨克（Gay J －Lussac J ）定律 在物质的量与压力恒定的条件下，气体的体积与热力学温度成正比，即V/T =常数 （n , p 一定）（3）阿伏加德罗（Avogadro A ）定律 在相同的温度、压力下，1mol 任何气体占有相同体积，即V / n =常数 （T ，p 一定）将上述三个经验定律相结合，整理可得到如下的状态方程：p V = n RT （1 .1 .1a ）上式称为理想气体状态方程。

物理化学主要公式

物理化学主要公式

物理化学主要公式第一章 气体的pVT 关系1.理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ，V ，T 及n 单位分别为Pa ，m 3，K 及mol 。

m /V V n =称为气体的摩尔体积，其单位为m 3 · mol -1。

R =8.314510 J · mol -1 · K -1，称为摩尔气体常数。

此式适用于理想气体，近似地适用于低压的真实气体。

2.气体混合物 （1） 组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B *=V ϕ∑*AVy Am ,A式中∑AA n 为混合气体总的物质的量。

A m,*V 表示在一定T ，p 下纯气体A 的摩尔体积。

∑*AA m ,A V y 为在一定T ，p 下混合之前各纯组分体积的总和。

（2） 摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量，∑=BB n n 为混合气体总的物质的量。

上述各式适用于任意的气体混合物。

（3）V V p p n n y ///B B B B *=== 式中p B 为气体B ，在混合的T ，V 条件下，单独存在时所产生的压力，称为B 的分压力。

*B V 为B 气体在混合气体的T ，p 下，单独存在时所占的体积。

3.道尔顿定律p B = y B p ，∑=BB p p上式适用于任意气体。

对于理想气体V RT n p /B B =4.阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。

5.范德华方程RT b V V a p =-+))(/(m 2mnRT nb V V an p =-+))(/(22式中a 的单位为Pa · m 6 · mol -2，b 的单位为m 3 · mol -1，a 和b 皆为只与气体的种类有关的常数，称为范德华常数。

气体的pVT关系及其应用

气体的pVT关系及其应用


水蒸气的分压 pD 2.670kPa 。
nA / nB 0.89 / 0.02
nA /(nA nB ) 0.89 /(0.89 0.02) 0.89 / 0.91
pA pB p pD (101.325 2.670)kPa 98.655kPa
对于混合混合压力之比等于物质的量之比，故
Vm p
TB
在T

TB
下，当压力趋于零时，上式中的

Vm p
TB

0 ，故必然存在
由上式可得
RTB Vm b

RTBVm (Vm b)2
a Vm2
0
a RTBVm RTB Vm2 (Vm b)2 Vm b
1.15 试由波意耳温度 TB 的定义式，证明范德华气体的 TB 可表示为 TB a / bR
式中 a,b 为范德华常数。
证：当T TB 时任一真实气体有
范德华方程可表示为
lim{
p0
(
pVm
)
/
p}TB
0
pVm RTVm (Vm b) a /Vm
上式在 T TB 下对 p 微分可得
解： CO2 (g) 的范德华常数 a 0.3640Pa m6 mol2 ；
b 0.4267 104 m3 mol1
( p a /Vm2 )(Vm b) RT
p RT /(Vm b) aVm2 {8.3145 313.15 /(0.381103 0.4267 104 ) 0.3640 /(0.381103)2}Pa 5187.7kPa
先将范德华方程整理成
p (RT /Vm ){1/(1 b /Vm )} a /Vm2
第五版物理化学第一章习题答案

第五版物理化学第一章习题答案

第一章气体的pVT关系1.1 物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的，与压力、温度的关系。

解：根据理想气体方程1.2 气柜内贮有121.6 kPa，27℃的氯乙烯（C2H3Cl）气体300 m3，若以每小时90 kg的流量输往使用车间，试问贮存的气体能用多少小时？解：假设气柜内所贮存的气体可全部送往使用车间。

1.3 0℃，101.325kPa的条件常称为气体的标准状况，试求甲烷在标准状况下的密度？解：将甲烷(M w=16g/mol)看成理想气体：PV=nRT , PV =mRT/ M w甲烷在标准状况下的密度为=m/V= PM w/RT=101.325⨯16/8.314⨯273.15(kg/m3)=0.714 kg/m31.4 一抽成真空的球形容器，质量为25.0000g充以4℃水之后，总质量为125.0000g。

若改充以25℃，13.33 kPa的某碳氢化合物气体，则总质量为25.0163g。

试估算该气体的摩尔质量。

水的密度1g·cm3计算。

解：球形容器的体积为V=（125-25）g/1 g.cm-3=100 cm3将某碳氢化合物看成理想气体：PV=nRT , PV =mRT/ M wM w= mRT/ PV=(25.0163-25.0000)⨯8.314⨯300.15/(13330⨯100⨯10-6)M w =30.51(g/mol)1.5 两个容积均为V 的玻璃球泡之间用细管连结，泡内密封着标准状态下的空气。

若将其中的一个球加热到 100℃，另一个球则维持 0℃，忽略连接细管中气体体积，试求该容器内空气的压力。

解：由题给条件知，（1）系统物质总量恒定；（2）两球中压力维持相同。

标准状态：因此，1.6 0℃时氯甲烷（CH 3Cl ）气体的密度ρ随压力的变化如下。

试作p p-ρ图，用外推法求氯甲烷的相对分子质量。

1.7 今有20℃的乙烷－丁烷混合气体，充入一抽成真空的200 cm3容器中，直至压力达101.325 kPa，测得容器中混合气体的质量为0.3897 g。

第1章气体的pVt关系

第1章气体的pVt关系


1.4.1 Van der Waals 方程 2 n ( p a 2 )(V nb) nRT V
b为1mol气体分子自身体积的影响。 分子间吸引力正比于(n/V)2 内压力 p′=a(n/V)2 pideal=preal+a(n/V)2 Van der Waals方 1 ( p a )( V b ) RT m 2 种的另一种形式 V
p1 p2 189 186 100% 1.61% p2 186 ’ 3 V 2.00dm3 p1 1.89103 kPa p’ 1 . 59 10 kPa 2
’ ’ 3 p1 p２ (1.89 1.59) 10 100% 18.9% ’ 3 p２ 1.59 10
a (p )(Vm b) RT 2 TVm
22
1.5压缩因子与普遍化压缩因子图
1.5.1真实气体的pVm-p图及波义尔温度
pVm/[pVm] C B A pVm/[pVm]
TB
p/[p]
图1.5.1不同气体在同一温度
下的pVm-p等温线
p/[p]
图1.5.2同一种气体在不同温度 下的pVm-p等温线
第1章 气体的p-T-V关系
1.1理想气体状态方程
低压下气体的三个经验定律： 1）Boyle定律：
pV=常数 V/T=常数 V/n=常数
（n、T一定） （n、p一定） （T、p一定） pV= nRT
R—通用气体常数
2）Gay-Lussac定律： 3）Avogadro定律：
精确值：R=（8.314510±0.000070）J· mol-1· K-1
mB wB def mA
A
nB xB (或yB ) def nA
第1章气体的PVT关系要点

第1章气体的PVT关系要点

B
•气体混合物中某组分的分压力(partial pressure)：
p p B pB y B p
B
nB RT pB V
pBV nB RT
•道尔顿(Dalton)分压定律：理想气体混合物中某组分 分压，为该组分单独存在于混合气体温度及总体积时 所具有的压力；混合气体总压等于各气体分压之和。
g
③ 临界摩尔体积(Vm,c): •Tc ，pc下物质的摩尔体积。
Vm 真实气体 p –Vm 等温线示意图
３、真实气体的临界状态
临界点的特征
•气液界面消失，气液性质完全 相同，气液不分； •数学中的拐点：
l´ 1 l´ 2
T1<T2<Tc<T3<T4
p
c
l2 l1 g2 g1
T4 T3 Tc T2 T1 g ´ 2
g´ 1
p 0 Vm Tc
2 p V 2 0 m Tc
l
g
Vm 真实气体 p –Vm 等温线示意图
超临界流体 (Super-critical Fluid)
•温度和压力略高于临界点的状态； •超临界流体兼具气液双重特性，高密度，扩散系 数大，具有很好的溶解性能； •超临界流体技术： ① 超临界萃取(extraction) ② 超临界流体干燥
１、理想气体（ perfect gas ）
分子间力（intermolecular force） •吸引力- 分子相距较远时，有范德华引力； •排斥力 分子相距较近时，电子云及核产生排斥作用。 Lennard-Jones 理论：
A B E E吸引＋E 排斥 6 12 r r E : 分子间相互作用总势能 A, B：吸引和排斥常数 r：分子间距

第一章 大学物理化学


3. 范德华方程 (1) 范德华方程 理想气体状态方程 : 实质为： 实质为： ( 分子间无相互作用力时的 气体压力 × ( 1mol 气体压力) 气体分子的自由活动空间 ) ＝ RT PVm＝RT
实际气体： 分子间有相互作用力 主要是吸引长程力) 分子间有相互作用力(主要是吸引长程力 实际气体：1.分子间有相互作用力 主要是吸引长程力
例题：管道输送天然气，输送压力为 例题：管道输送天然气，输送压力为200KPa，T＝ ， ＝ 25℃时，管道内的天然气密度是多少？(近似将天 管道内的天然气密度是多少？ 近似将天 ℃ 然气视作纯甲烷) 然气视作纯甲烷 解： M 甲烷＝1.604×10 －2Kg.mol－1
P 3 −2 200 ×10 × 1.604 ×10 = 8.314 × 298.15
：
解：烃类气体的分压为 PA ，水蒸气分压 PB PB＝ 3.167KPa , PA＝ P －PB＝101.198KPa
nB ⋅P a) 由公式 P B＝ yB P = ∑ nB
Hale Waihona Puke 可得nB PB = n A PA
⇒
PB nB = ⋅ nA PA
3.167 B nB = ×1000 mol = 31.30 mol 101.198
分子间相互作用减弱了分子对器壁的碰撞， 分子间相互作用减弱了分子对器壁的碰撞，使气体压力 减小； 减小；可将这种由于分子间相互吸引力对压力的影响理 解为内压力 内压力， 解为内压力，P内 P内＝a / Vm2 a > 0 范德华常数 , 单位Pa . m6. mol-2
实际测定压力值 P ＝ P理－ P内, P理 ＝ P + P内 ＝ P + a / Vm2
气体
{

气体的PVT关系专业知识

3.普遍化压缩因子图
压力—临界压力(pc), pc(CO2)=7.38MPa 体积—临界摩尔体积(Vm,c),Vm,c(CO2)=94×10-6m3·mol-1
Tc , pc , Vm,c 统称临界参量。某些物质旳临界参量见表1.2。
表1.2 某些物质旳临界参量
物质
He H2 N2 O2 H2O CH4 C2H 4 C6H6 C2H5 OH
第一章 气体旳PVT关系 1.1 理想气体旳状态方程及微观模型
1.理想气体旳状态方程
PV=nRT
PVm=RT PV=mRT/M
R=8.3145J.K-1.mol-1
对于混合气体旳摩尔质量 Mmix=∑yBMB
例如
空气 y(O2)=0.21 y(N2)=0.79
则 M(空气)= y(O2) ×MO2+ y(N2) ×MN2=0.21×32+0.79×28
a=27R2Tc2/64pc, b=RTC/8Pc
3.维里方程
pVm
RT (1 B Vm
C Vm2
D Vm3
)
pVm RT (1 Bp Cp2 Dp3 )
4.其他主要方程举例
1.5 相应状态原理及普遍化压缩因子图
1.压缩因子
pV ZnRT或pVm ZRT
Z pV pVm nRT RT
以温度T1为例，曲线分为三段：
T1T2Tc T3
加压
{p} c
g(气体) 体积缩小 a(饱和气体)
l
定压
a(饱和气体)体积明显缩小 b(饱和液体)
b
a g
加压 b(饱和液体) 体积缩小(较小) l(液体)
{Vm,c} 图1-3 CO2 定温p-Vm,c 图

第一章 气体的PVT关系


27R 2TC2 RTC a ，b 64 pC 8 pC
4.维里方程

维里方程是卡末林-昂尼斯于20世纪初作为纯经验方程提 出的，有两种形式：
B C D pVm RT 1 V V 2 V 3 ..... m m m pVm RT 1 B ' p C ' p 2 D ' p 3 .....
a，b分别为范德华常数，只与气体的种类有关，与温度条 件无关。
3.范德华常数与临界参数的关系

临界点是拐点，临界点处的一阶、二阶导数为零
p V m 2P 0， V 2 m TC 0 TC
a 27 b 2
Vm ,C
8a 3b, TC , pC 27 Rb
对理想气体，在任何温度、压力下Z值恒为1，当Z<1时, 说明真实气体比理想气体易于压缩;当Z>1时,说明真实气 体比理想气体难于压缩;
将压缩因子概念应用于临界点,可得出临界压缩因子ZC
ZC
pCVm,C RTC
2.对应状态原理

对比压力:pr=p/pc 对比温度:Tr=T/TC 对比体积:Vr=Vm/Vm,C 对应状态原理:各种不同得气体,只要有两个对比参 数相同,则第三个对比参数必定相同。
临界状态: 压力—临界压力(pc), pc(CO2)=7.38MPa 体积—临界摩尔体积(Vm,c),Vm,c(CO2)=94×10-6m3· mol-1 Tc , pc , Vm,c 统称临界参量。一些物质的临界参量见表1.2。
表1.2 一些物质的临界参量 物 He 质 Tc/K 5.26 pc/MPa 0.229 Vm,c/10-6m3· mol-1 58

1气体的pvt关系


不 可 无 限 压 缩
2.理想气体 理想气体(perfect gas)模型 理想气体 模型
①分子之间无作用力 分子之间无作用力 ②分子本身不占体积 分子本身不占体积 分子可近似被看作 是没有体积的质点 质点， 质点 实际上的理想气体是不 存在的，它只是一种假 想的气体，可看作是真 实气体在压力趋于零时 的极限情况。
压缩因子反应真实气体对理想气体的偏差程度 Z<1，说明真实气体比理想气体易于压缩； Z>1说明真实气体比理想气体难以压缩。 实测大多数物质的Zc约为0.26-0.29。 由临界参数定义及范德华常数带入得： Zc＝3/8=0.375
2.对应状态原理 2.对应状态原理
对比压力： 对比体积： 对比温度：
无论物质出于何种状态，都有许多宏观性质， 如压力p，体积V，温度T，密度ρ，热力学能U等。 其中p，V，T是物理意义非常明确、又易于直接测 量的基本性质。对一定量的纯物质，只要中p，V， T任意两个确定后，第三个量就随之确定，此时就 说物质处于一定的状态。联系p，V，T之间关系的 方程称为状态方程。
× × ×
× × × × ×
× × × ×
可 无 限 压 缩
×
• 理想气体的状态方程是理想气体的宏观外在 表现 • 理想气体的微观模型反映了理想气体的微观 内在本质 • 理想气体是真实气体在 p→ 0 情况下的极 限状态。
3.摩尔气体常数（gas constant) 摩尔气体常数（ 摩尔气体常数
∂p ∂2 p =0 = 0, 2 ∂Vm TC ∂Vm TC
§1.4 真实气体状态方程
1.真实气体的 pVm − p 图及波义耳温度
波义耳温度：在此温度下，当压力趋于零时， pVm − p 等温线的斜率为零。波义耳温度一般 为气体临界温度的2－2.5倍。

物理化学重要知识点总结及其考点说明

第一章气体的pvT关系⑴波义尔定律：当n、T一定时，PV=常数⑵盖-吕萨克定律：当n、P一定时，V/T=常数⑶阿伏伽德罗定律：当T、P一定时，V/n=常数●⑷理想气体状态方程：PV=（m/M）RT= nRT或者或PVm=p（V/n）=RTR=8.314mol-1·K-1称为摩尔气体常数；T为华氏温度⑸摩尔分数：X B=n B/n总●⑹道尔顿定律：P B=P总X B;P总=P分⑺实际气体状态方程：PV=znRT（z为压缩因子）●⑻理想气体特征：①分子间无相互作用力②分子本身不占有体积第二章热力学第一定律热力学第一定律（能量守恒定律）●⑴系统：①隔离系统：无能量、无物质交换②★封闭系统：有能量、无物质交换（热力学基础；热力学研究对象）③敞开系统：有能量、有物质交换●⑵状态函数：P、V、T、U、H、G、A、S (P、T、C p, m、C V，m 为强度量，其他均为广度量) 状态函数特征：①有可微分性，能计算②只与始末状态有关●途径函数：Q、W●⑶热：系统从环境中吸热（Q＞0）；系统对环境做功（W＜0）●⑷热力学能：△U=Q+W（封闭系统）；U只是温度T的函数；只与首末有关非体积功的计算①气体向真空膨胀时体积功所的计算W=0②恒外压过程体积功W=-p（V2-V1）=-p△V③对于理想气体恒压变温过程W=-p△V=-nR△T④可逆过程体积功W=-p（v2-v1）●⑤理想气体恒温可逆过程体积功 W=-p（v2-v1）或者W=-nRTln(V1/V2)或者W=nRTln（p2/ p1）⑥理想气体绝热可逆过程体积功W=-p（v2-v1）=（-）γ= C p, m /C V，m（双原子气体为1.4）T2/T1=(V1/V2) 的γ-1次方；T2/T1=(P1/P2)的（γ-1）/γ次方；P2/P1=(V1/V2)的γ次方●⑦恒温膨胀可逆功最大，系统对环境作最大功；恒温可逆压缩，环境对系统做最小功⑧可逆相变体积功W=-pdV恒热容、恒压热，焓⑴焓定义：H=U + PV⑵焓变：△H=△U+△(pV)式中△(pV)为p V乘积的增量，只有在恒压下△(pV)=p(V2-V1)在数值上等于体积功。

物化第一章习题


M RT / p 8.315J K 1mol 1 273.15K 22.237 10 6 kg m 3 Pa 1 50.5 10 3 kg mol 1 50.5g mol 1
22.8 22.7
1.7 今有 20℃的乙烷-丁烷混合气体，充入一 抽成真空的 200cm3 容器中，直至压力达 101.325kPa， 测得容器中混合气体的质量为 0.3897g。试求该混合气 体中两种组分的摩尔分数及分压力。 解：已知 T=293.15K V=0.2dm3=2.0×10-4m3 p=101.325kPa m=0.3897g=3.897×10-4kg
《物理化学》
第一章 气体的 pVT 关系
第 4 页
因为 pV=(m/Mg)RT 所以 Mg =mRT/pV=8.315Pam3mol-1K-1×298.15K×0.0163g/13330Pa×0.0001m3 =30.31 gmol-1 1.5 两个容积均为 V 的玻璃球泡之间用细管连接， 泡内密封着标准状况下的空气。 若将其中一个球加热到 100℃，另一个球则维持 0℃，忽略连接细管中气体体积，试求该 容器内空气的压力。
25.331 0.56660
2.3074 1.5263 1.1401 /g.dm 解：当气体符合理想气体的行为时 p mRT /(VM ) 所以 M RT / p
对于实际气体，只有当压力 p 趋近于零时上述关系才成立，即 由题所给数据计算出在不同压力下的/p 值。列表如下： p/kPa
n
A A
A
yB 表示气体；xB 表示液体
B y BVm ，B / y AVm，A
（ii）混合物摩尔质量
M mix y B M B m / n m B / n B
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

V受T,p 的影响较小 （又称凝聚态）
p — pressure（压强）
V — volume（体积）
T — temperature（温度）
联系物质p、V、T 之间关系的方程称为
状态方程（equation of state)。
§1.1 理想气体状态方程
pV nRT
1、理想气体模型 ２、理想气体状态方程 ３、摩尔气体常数
第一章 气体的pVT关系
§1.1 理想气体状态方程 §1.2 理想气体混合物 §1.3 真实气体的液化及临界参数 §1.4 真实气体状态方程 §1.5 对应状态原理及普遍化压缩因子图
第一章 气体的pVT关系
物质的聚集状态
气体 (gas) V受T,p 的影响很大
液体 (liquid)
固体 (solid)
r：分子间距
r0
r
１、理想气体（ perfect gas ）
理想气体微观模型
注意
① 分子之间无相互作用力； ② 分子本身不占有体积。
理想气体是一种假想的科学模型； 理想气体可看作真实气体压力趋于零的极限情况； 低压，或高温气体可近似作为理想气体处理。
2、理想气体状态方程
•低压气体三大经验定律： ① 波义尔定律(R.Boyle，1662):
1、混合物组成表示法 2、道尔顿分压定律 3、阿马加分体积定律
1、混合物组成表示法
①
摩尔分数 xB 或yB： xB ( yB ) (mole fraction)
nB
nB
B
xB 1
B
yB 1
B
② 质量分数 ωB： B (weight fraction)
mB mB
B
B 1
B
③ 体积分数 B：
pV ( B nB )RT M mix RT
Mmix yB MB
B
➢以理想气体混合物中任一组分为研究对象：
•道尔顿分压定律： pBV nB RT
•阿马加分体积定律： pVB nB RT
pB p
VB V
yB
课后作业
P18：
习题1.3，1.4，1.6
重点内容回顾
１、理想气体模型
① 分子之间无相互作用力； ② 分子本身不占有体积。
pV ＝ 常数 ( n ,T一定）
② 盖-吕萨克定律(J. Gay-Lussac，1808)：
V / T ＝ 常数 (n , p一定) ③ 阿伏加德罗定律（A. Avogadro，1811)
V / n ＝ 常数 (T, p一定)
f ( p,V ,T , n) 0 或 V ( p,T , n)
2、理想气体状态方程
pV 常数 R pV nRT
nT
2、理想气体状态方程
•理想气体状态方程： pV nRT
单位：p Pa；V m3； T K； n mol ； R 摩尔气体常数 8.314J mol-1 K-1
理想气体宏观定义
任何温度、压力下均服从理想气体状态方程的气态方程： pV nRT
N2
He CH4
理想气体
p0时：pVm = 2494.35 Jmol-1
2 0 0 0
1 5 0 0
R pVm / T 8.3145J mol1 K 1 1 0 0 0
0 2 0 4 0 6 0 8 0 1 0 0 1 2 0
R 是一个对各种气体都适用的常数。 p / MPa
§1.2 理想气体混合物
3、摩尔气体常数（molar gas constant）
外推法确定R值
300K时N2、He、CH4 的pVm-p等温线
•一定温度下测气体不同压力p 时 摩尔体积Vm ，将pVm 对p 作图；
•外推到p 0处求出pVm ，从
而计算得R：
5 0 0 0 4 5 0 0 4 0 0 0 3 5 0 0 3 0 0 0 2 5 0 0
p n RT cRT V
pVm RT
pV m RT M
pM RT
适用条件 理想气体，或低压、高温真实气体！
3、摩尔气体常数（molar gas constant）
• 理想气体状态方程： pVm RT
问题
摩尔气体常数R值如何确定？
➢原则上：
真实气体：
lim
p0
pVm
RT
➢实际上： 当p 0,V （数据不准确）
•低压气体三大定律： V ( p,T , n)
dV
V p
T
,n
dp
V T
dT p,n
V n
dn T , p
波义尔 盖吕萨克 阿伏加德罗
dV V dp V dT V dn
pT
n
dV dp dT dn ( dx d ln x)
V
pT n
x
d ln pV 0 nT
２、理想气体状态方程
pV nRT
３、理想气体混合物分压、分体积定律
pBV nB RT
pVB nB RT
pB p
VB V
yB
本堂课学习内容
§1.3 气体的液化及临界参数 §1.4 真实气体状态方程 §1.5 对应状态原理及普遍化压缩因子图
B
pV ( nB )RT B
VB yBV
VB*
nB RT p
pVB nB RT
•阿马加分体积定律：理想气体混合物某组分的分体积，
为该组分单独存在于混合气体温度Ｔ及总压Ｐ时所具
有体积；混合气体总体积为各组分分体积之和。
理想气体状态方程对理想气体混合物的应用
➢以理想气体混合物整体为研究对象：
m
B
pB
nB RT V
pBV nB RT
•道尔顿(Dalton)分压定律：理想气体混合物中某组分 分压，为该组分单独存在于混合气体温度及总体积时 所具有的压力；混合气体总压等于各气体分压之和。
3、阿马加分体积定律（1880年）
•理想气体混合物中某组分的分体积（partial volume）：
V VB*
(volume fraction)
B
x BVm* , B x BVm* , B
B
B 1
B
2、道尔顿分压定律（1810年）
•理想气体混合物状态方程：
pV
(
B
nB )RT
m M mix
RT
Mmix yB MB
B
•气体混合物中某组分的分压力(partial pressure)：
p pB pB yB p
１、理想气体（ perfect gas ）
分子间力（intermolecular force）
•吸引力- 分子相距较远时，有范德华引力；
•排斥力- 分子相距较近时，电子云及核产生排斥作用。
Lennard-Jones 理论：
E
E吸引＋E排斥
A r6
B r12
E
E :分子间相互作用总势能 0
A, B：吸引和排斥常数