四川大学计算机学院 离散数学(第14讲)
- 格式:ppt
- 大小:681.00 KB
- 文档页数:24


习题十1. 设G 是一个(n ,m)简单图。
证明:,等号成立当且仅当G 是完全图。
证明:(1)先证结论:因为G 是简单图,所以G 的结点度上限 max(d(v)) ≤ n-1, G 图的总点度上限为 max(Σ(d(v)) ≤ n ﹒max(d(v)) ≤ n(n-1) 。
根据握手定理,G 图边的上限为 max(m) ≤ n(n-1)/2,所以。
(2) =〉G 是完全图 因为G 具有上限边数,假设有结点的点度小于n-1,那么G 的总度数就小于上限值,边数就小于上限值,与条件矛盾。
所以,G 的每个结点的点度都为n-1,G 为完全图。
G 是完全图 =〉 因为G 是完全图,所以每个结点的点度为n-1, 总度数为n(n-1),根据握手定理,图G 的边数 。
■2. 设G 是一个(n ,n +1)的无向图,证明G 中存在顶点u ,d (u )≥3。
证明:反证法,假设,则G 的总点度上限为max(Σ(d(u)) ≤2 n ,根据握手定理,图边的上限为max(m) ≤ 2n/2=n 。
与题设m = n+1,矛盾。
因此,G 中存在顶点u ,d (u )≥3。
■3.确定下面的序列中哪些是图的序列,若是图的序列,画出一个对应的图来: (1)(3,2,0,1,5); (2)(6,3,3,2,2) (3)(4,4,2,2,4); (4)(7,6,8,3,9,5)解:除序列(1)不是图序列外,其余的都是图序列。
因为在(1)中,总和为奇数,不满足图总度数为偶数的握手定理。
可以按如下方法构造满足要求的图:序列中每个数字ai 对应一个点,如果序列数字是偶数,那么就在对应的点上画ai/2个环,如果序列是奇数,那么在对应的点上画(ai-1)/2个环。
最后,将奇数序列对应的点两两一组,添加连线即可。
下面以(2)为例说明:(6 , 3, 3, 2, 2 ) 对应图G 的点集合V= { v 1,v 2,v 3,v 4,v 5}每个结点对应的环数(6/2, (3-1)/2, (3-1)/2, 2/2,2/2) = (3,1,1,1,1)v 1v 5v 3v 4v 2将奇数3,3 对应的结点v 2,v 3一组,画一条连线其他序列可以类式作图,当然大家也可以画图其它不同的图形。



习题一鮮答或提示1•⑴设P:他是本片的编剧,Q:他是本片的导決。
P A Q(2) 瑕P:级行利率吟低.Q:肢价上扬。
P→Q(3) 沒P:级行利率阵低.Q:股价上升。
〜(P→Q)(4) 设P:这个对象是占堀空问的∙Q:这个对象是有质量的R:这个对象是不飾变化的、S:这个对象称为场填。
P A Q A R→S(5) 沒P:他今天乘火车去了,Q:他今天随嵌行团去了九杀沟。
PVQ(6) 瑕P:小身体单萍,瑕Q:小圾少生病■没R:小头脑好使。
P A Q A R(7) 役P:这个人不枳庐丄真面Iu 设Q:这个人身A庐丄中。
QTR(8) 锻P:両个三角形柯似.没Q:两个三角形的对应角相普或者对应边成比例。
P<→Q(9) 沒P:-个整數能彼6整除,沒Q:这个整欽能彼2和3整除。
P→Q设R:-个整數能後3整徐,很S:这个整数的各住.数字之和也能彼3整除。
RTS2、(1)命題T(2) 命题T/F(3) 不是命题,因为真值无出确主。
⑷命题T(5)不是命题。
⑹命题T(7) 命题T/F(8) 不是命題,是悸论。
5、CU 证:〜((〜PAQJ V (〜PA〜Q丿)V CPAQJO (〜C〜PAQJ A〜(〜PA〜Q丿)V CPAQ丿o ( CPV 〜Q丿A CPVQJ ) V (PAQJO CPV (〜QVQJ ) V (PAQ)OPV CPAQ) OP(3) ⅛: Pf(QVR)o 〜PV(QVR)O 〜PVQV 〜P∖∕Ro C〜PVQJ V C〜PVR丿O(PfQ丿V (PfR丿6. 解:如系PVQoQ∖∕R∙不能靳走POR。
Q=T⅛, PVQ O QVR艳成立。
⅛r> PΛQ<=>QΛR,不能餅丈PoRO 因Q=F J⅛,PAQ O QAR怛成丈。
如系〜Po〜R, JK PORo8、把下刃冬丸用f寻价表承出来:(1) 豹CPAQJ 7〜TO C(PfQ) f (Pf Q丿V CPfP丿OCC(PfQf(PfQ)丿t C(PfQ)I(PtQ)J ) t (CPtPJ t (P↑?)) ⑶鮮:CP→ (QV〜R丿)A〜PO (〜PV (QV〜R丿)A〜Po ( CPtPJ V ΓQV CRtRJ )丿A (PtPJ ;O((PfP丿V ( CQ↑QJ t (CRtR) ↑ (^↑R) ) ) ) A CPtPJo ( ( CPtPJ t CP↑P> JtCC (QtQJ t ( (Rf R丿↑ CRtR) ) ) ↑(CQtQ) t ( (RfR丿t CRfR丿))))^ CPtP)OCL CPtPJ t CPtP) JtCr CQtQJ t ( CRtRJ t CRfR丿))↑ (ΓQtQJ ↑ ( CR↑RJ t CRfR丿))))↑(PW JtCCr CPtPJ ↑ (PfP丿) t (((Q↑Q) ↑ CCRtR丿t fR↑RJ ) ) ↑( CQtQJ t CfRfR丿t CRtRJJ))J t CPtP))9. ⅛E: ∙.∙ PVQ<=>---------- P VQ<=> (r~P∕ →QPAQ<≡>~ (〜PV〜Q丿O〜CPf〜Q丿而{〜,V,八}是功能克备.°.{〜,f}是功能完务集,〜,一►不能JL相表示,故{〜・f}是最小功能克备為。


《离散数学》教学大纲安徽大学计算机科学与技术学院二OO六年六月前言《离散数学》课程是计算机科学与技术专业高等教育的专业基础课程。
《离散数学》是现代数学的一个重要分支,是学习计算机科学与技术专业理论必不可少的数学工具。
本课程主要研究离散对象的结构及相互关系,对提高学生的抽象思维与逻辑推理能力有重要作用。
设置本课程的目的是:培养学生的数学思维能力,使学生得到良好的数学训练,提高学生的抽象思维和逻辑推理能力,并使学生掌握处理离散结构所必须的描述工具和方法,为其从事计算机的应用提供坚实的理论基础。
学习本课程的要求是:通过本课程的学习,学生应正确理解和熟练掌握基本概念、基本定理及其证明方法,提高运用基本理论分析和解决实际问题的能力,为在后续专业课和实际工作中运用本课程的基本知识打下基础。
先修课程要求:高等数学。
本课程计划144学时,7学分,分两学期完成,分别称为离散数学(上)和离散数学(下)。
离散数学(上)计划72学时,3.5学分;离散数学(下)计划72学时,3.5学分。
选用教材:《离散数学》,方世昌,西安电子科技大学出版社,2000出版。
教学手段:多媒体教学。
考核方法:考试。
教学进程安排表:第一章数理逻辑一、学习目的通过本章的学习,理解命题、联结词、命题公式、(主)析/合取范式、个体、谓词、量词、谓词公式、指派等概念;掌握公式真值表的构造及命题符号化方法、常用的基本等值式及其应用、常用的永真蕴涵式及其在逻辑推理中的应用、(主)析/合取范式的计算、命题演算和谓词演算的推理规则和证明方法。
第一章计划26学时。
二、课程内容1.1 命题(一)命题的概念。
(二)命题联结词及其真值表。
(三)命题符号化。
(四)命题变元和命题公式的概念。
1.2 重言式(一)指派、重言式、逻辑恒等式、永真蕴含式等基本概念。
(二)常见的逻辑恒等式和永真蕴含式。
(三)逻辑恒等式和永真蕴含式的基本性质。
(四)命题演算的基本规则:代入规则、替换规则。

习题一解答或提示1. (1) 设P:他是本片的编剧,Q: 他是本片的导演。
P∧Q(2) 设P:银行利率降低,Q:股价上扬。
P→Q(3) 设P:银行利率降低,Q:股价上升。
~(P→Q)(4) 设P:这个对象是占据空间的,Q: 这个对象是有质量的,R: 这个对象是不断变化的,S: 这个对象称为物质。
P∧Q∧R→S(5) 设P:他今天乘火车去了,Q: 他今天随旅行团去了九寨沟。
P∇Q(6) 设P:小身体单薄,设Q:小极少生病, 设R:小头脑好使。
P∧Q∧R(7) 设P:这个人不识庐山真面目,设Q:这个人身在庐山中。
Q→R(8) 设P:两个三角形相似, 设Q:两个三角形的对应角相等或者对应边成比例。
P↔Q(9) 设P:一个整数能被6整除,设Q:这个整数能被2和3整除。
P→Q设R:一个整数能被3整除,设S:这个整数的各位数字之和也能被3整除。
R→S 2、(1) 命题T(2) 命题T/F(3) 不是命题,因为真值无法确定。
(4) 命题T(5) 不是命题。
(6) 命题T(7) 命题T/F(8) 不是命题,是悖论。
5、(1)证:~((~P∧Q)∨(~P∧~Q))∨(P∧Q)⇔(~(~P∧Q)∧~(~P∧~Q))∨(P∧Q)⇔((P∨~Q)∧(P∨Q))∨(P∧Q)⇔(P∨(~Q∨Q))∨(P∧Q)⇔ P∨(P∧Q)⇔P(3)证:P→(Q∨R)⇔~P∨(Q∨R)⇔~P∨Q∨~P∨R⇔(~P∨Q)∨(~P∨R)⇔ (P→Q)∨(P→R)6、解:如果P∨Q⇔Q∨R,不能断定P⇔R。
因为当Q=T时,P∨Q⇔Q∨R恒成立。
如果P∧Q⇔Q∧R,不能断定P⇔R。
因为当Q=F时,P∧Q⇔Q∧R恒成立。
如果~P⇔~R,则P⇔R。
8、把下列各式用↑等价表示出来:(1)解:(P∧Q)∨~P⇔(( P↑Q)↑( P↑Q))∨(P↑P)⇔((( P↑Q)↑( P↑Q))↑(( P↑Q)↑( P↑Q)))↑((P↑P)↑(P↑P))(3)解:(P→(Q∨~R))∧~P⇔(~P∨(Q∨~R))∧~P⇔((P↑P)∨(Q∨(R↑R)))∧(P↑P);⇔((P↑P)∨((Q↑Q)↑((R↑R)↑(R↑R))))∧(P↑P)⇔(((P↑P)↑(P↑P))↑(((Q↑Q)↑((R↑R)↑(R↑R)))↑((Q↑Q)↑((R↑R)↑(R↑R)))))∧(P↑P)⇔((((P↑P)↑(P↑P))↑(((Q↑Q)↑((R↑R)↑(R↑R)))↑((Q↑Q)↑((R↑R)↑(R↑R)))))↑(P↑P))↑((((P↑P)↑(P↑P))↑(((Q↑Q)↑((R↑R)↑(R↑R)))↑((Q↑Q)↑((R↑R)↑(R↑R)))))↑(P↑P))9、证:∵P∨Q⇔~~P∨Q⇔(~P)→QP∧Q⇔~(~P∨~Q)⇔~(P→~Q)而{~,∨,∧}是功能完备集,∴{~,→}是功能完备集,~,→不能互相表示,故{~,→}是最小功能完备集。


《离散数学》专科期末复习提要四川电大孙继荣2004年5月《离散数学》是四川电大数学与应用数学专业开设的课程。
使用的教材为中央电大出版的《离散数学》(刘叙华等编)和《离散数学学习指导书》(虞恩蔚等编)。
离散数学主要研究离散量结构及相互关系,使学生得到良好的数学训练,提高学生抽象思维和逻辑推理能力,为从事计算机的应用提供必要的描述工具和理论基础。
其先修课程为:高等数学、线性代数;后续课程为:数据结构、数据库、操作系统、计算机网络等。
课程的主要内容1、集合论部分(集合的基本概念和运算、关系及其性质);2、数理逻辑部分(命题逻辑、谓词逻辑);3、图论部分(图的基本概念、树及其性质)。
4、布尔代数(此部分对专科要求不高)学习建议离散数学是理论性较强的学科,学习离散数学的关键是对离散数学(集合论、数理逻辑和图论)有关基本概念的准确掌握,对基本原理及基本运算的运用,并要多做练习。
教学要求的层次各章教学要求的层次为了解、理解和掌握。
了解即能正确判别有关概念和方法;理解是能正确表达有关概念和方法的含义;掌握是在理解的基础上加以灵活应用。
一、各章复习要求与重点第一章集合[复习知识点]1、集合、元素、集合的表示方法、子集、空集、全集、集合的包含、相等、幂集2、集合的交、并、差、补等运算及其运算律(交换律、结合律、分配律、吸收律、De Morgan 律等),文氏(Venn)图3、序偶与迪卡尔积本章重点内容:集合的概念、集合的运算性质、集合恒等式的证明[复习要求]1、理解集合、元素、子集、空集、全集、集合的包含、相等、幂集等基本概念。
2、掌握集合的表示法和集合的交、并、差、补等基本运算。
3、掌握集合运算基本规律,证明集合等式的方法。
4、了解序偶与迪卡尔积的概念,掌握迪卡尔积的运算。
[疑难解析]1、集合的概念因为集合的概念学生在中学阶段已经学过,这里只多了一个幂集概念,重点对幂集加以掌握,一是掌握幂集的构成,一是掌握幂集元数为2n。
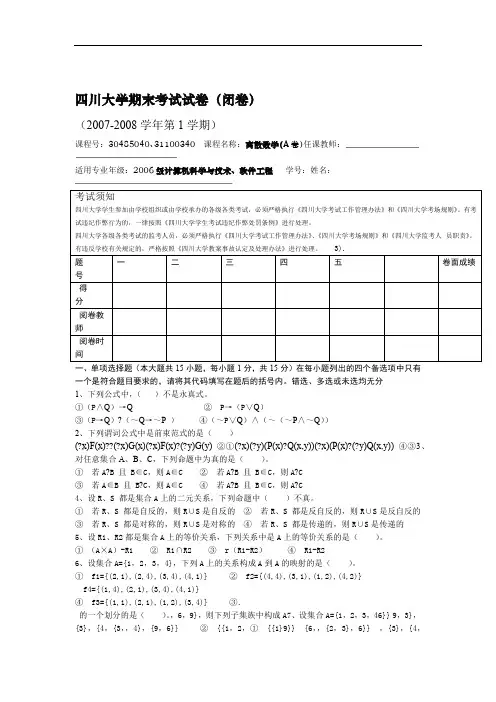
四川大学期末考试试卷(闭卷)(2007-2008学年第1学期)课程号:30485040、31100340 课程名称:离散数学(A卷)任课教师:适用专业年级:2006级计算机科学与技术、软件工程学号:姓名:考试须知一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分1、下列公式中,()不是永真式。
①(P∧Q)→Q ② P→(P∨Q)③(P→Q)?(~Q→~P )④(~P∨Q)∧(~(~P∧~Q))2、下列谓词公式中是前束范式的是()(?x)F(x)??(?x)G(x)(?x)F(x)?(?y)G(y)②①(?x)(?y)(P(x)?Q(x,y))(?x)(P(x)?(?y)Q(x,y))④③3、对任意集合A、B、C,下列命题中为真的是()。
①若A?B 且 B∈C,则A∈C ②若A?B 且 B∈C,则A?C③若A∈B 且 B?C,则A∈C ④若A?B 且 B∈C,则A?C4、设R、S 都是集合A上的二元关系,下列命题中()不真。
①若R、S 都是自反的,则R∪S是自反的②若R、S 都是反自反的,则R∪S是反自反的③若R、S 都是对称的,则R∪S是对称的④若R、S 都是传递的,则R∪S是传递的5、设R1、R2都是集合A上的等价关系,下列关系中是A上的等价关系的是()。
①(A×A)-R1 ② R1∩R2 ③ r(R1-R2)④ R1-R26、设集合A={1,2,3,4},下列A上的关系构成A到A的映射的是()。
① f1={(2,1),(2,4),(3,4),(4,1)} ② f2={(4,4),(3,1),(1,2),(4,2)}f4={(1,4),(2,1),(3,4),(4,1)}④ f3={(1,1),(2,1),(1,2),(3,4)} ③.的一个划分的是()。
,6,9},则下列子集族中构成A7、设集合A={1,2,3,46}} 9,3},{3},{4,{3,,4},{9,6}} ② {{1,2,① {{1}9}} {6,,{2,3},6}} ,{3},{4,9,④ {{1,2}③ {{1,2} )。