当前位置：文档之家 › 数学人教版八年级上册全等三角形的判定复习课精品PPT课件

数学人教版八年级上册全等三角形的判定复习课精品PPT课件

  • 格式：pptx
  • 大小：784.12 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

人教版 八年级数学上册第十二章：全等三角形复习课件(共15张PPT)

人教版 八年级数学上册第十二章：全等三角形复习课件(共15张PPT)

O
\ PD = PE
用途：证线段相等
E
角平分线性质的逆定理 到一个角的两边 的距离相等的点， 在这个角的平分线上。
∵ PD OA PE OB
PD = PE
\ OP 是 AOB 的平分线
用途：判定一条射线是角平分线
A C
P B
一、已知:如图∠B=∠DEF,BC=EF,补充条件 求证:ΔABC≌ ΔDEF (1)若要以“SAS”为依据，还缺条件 ＿A＿B=＿D＿E ＿； (2) 若要以“ASA”为依据，还缺条件∠＿A＿CB＿= ＿∠D；FE
E
O
B
C
6. 已知：BD⊥AM于点D，CE⊥AN于点E， BD、CE交于点F，CF=BF， 求证：点F在∠A的平分线上。
CM D
F
A
N EB
7、如图所示，DC=EC，AB∥CD，∠D=90°， AE⊥BC于E，求证：∠ACB=∠BAC．
8. 如图，四边形ABCD中，AC平分∠BAC， CE⊥AB于E，AD+AB=2AE， 求证：∠B与∠ADC互补。
2.如图（2），点D在AB上，点E在AC上， B
D
CD与BE相交于点O，且AD=AE,AB=AC.若 O
A
∠B=20°,CD=5cm，则 ∠C= 20°,BE= 5.说cm说理由.
E C 图（2）
3.如图（3），AC与BD相交于o,若
A
D
OB=OD，∠A=∠C，若AB=3cm3c，m 则
CD=
友情. 说提说示理：由公. 共边，公共角，B
(3) 若要以“AAS”为依据，还缺条件∠＿A＿=＿∠＿＿D ；
AD
B E CF
(4)若∠B=∠DEF=90°BC=EF,要以“HL” 为依据， 还缺条件＿A＿C=＿D＿F ＿

三角形全等的判定+课件 2024—2025学年人教版数学八年级上册

三角形全等的判定+课件 2024—2025学年人教版数学八年级上册
12.2三角形全等的判定
自主学习
小莲家的衣柜上镶有两块全等三角形玻璃 装饰物,其中一块被打碎了,妈妈让小明到 玻璃店配一块回来,请你说说小莲该怎么 办?
三角形全等的 判定方法
合作探究 怎样判定三角形全等呢？
①三边对应相等； ②三个角对应相等； ③两角一边； ④两边一角······
归纳总结 全等三角形的判定方法（1）
三边分别相等的两个三角形全等 简写成“边边边”或“SSS”
三角形三条边的长度确定 了，这个三角形的形状、 大小也就确定了。这就是 三角形的稳定性。
小莲家的衣柜玻璃 能解决了吗？
如图所示，用数学语言表示为：
A
在△ABC和△A'B'C'中，
AB=A'B' BC=B'C' AC=A'C'
B
C
A'
∴ △ABC≌△A'B'C'(SSS） B'
C 证明: 连接AB
在△ACB 和 △ADB中
AC = AD
A
B
BC = BD
AB = AB (公共边）
∴△ACB≌△ADB （SSS） ∴∠C＝∠D （全等三角形的对应角相等） D
用一用 1.工人师傅常用角尺平分一个任意角. 做法如下：如图， AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺， 使角尺两边相同的刻度分别与M，N重合. 过角尺顶点C的射线 OC便是 AOB的平分线.为什么？
AB=CD （已知）
A
B
AD=BC （已知）
BD=DB （公共边）
∴ ABD ≌ CDB （SSS）
∴ ∠A= ∠C （ 全等三角形的对应角相等 ）

人教版八年级上册数学《三角形全等的判定》全等三角形研讨说课复习课件

人教版八年级上册数学《三角形全等的判定》全等三角形研讨说课复习课件

A
A . 1个
B. 2个
C. 3个
D. 4个
D
O
B
C
课堂检测
能力提升题
1. 已知：如图，AB=AE，AC=AD，BD=CE，
求证：△ABC ≌△AED.
证明：∵BD=CE,
=×
∴BD－CD=CE－CD .
∴BC=ED .
在△ABC和△ADE中，
AC=AD（已知），
AB=AE（已知），
BC=ED（已证），
30◦
4cm
30◦
4cm
结论:一条边一个角对应相等的两个三角形不一定全等.
探究新知
③如果三角形的两个内角分别是30°，45°时
30◦
45◦
30◦
45◦
结论:两个角对应相等的两个三角形不一定全等.
根据三角形的内角和为180°，则第三角一定确定，
所以当三个内角对应相等时，两个三角形不一定全等.
探究新知





AB＝AC，
AD＝AE，
BD＝CE，
∴ △ ABD≌ △ ACE(SSS)，
∴∠BAD＝∠CAE.
∴∠BAD＋∠DAC＝∠CAE＋∠DAC，
即∠BAC＝∠DAE.
巩固练习
已知：如图，AB=AD，BC=DC，
求证：△ABC≌△ADC，AC是∠BAD的角平分线.
证明：在△ABC和△ADC中
AB=AD, (已 知 )
A′
探究新知
用尺规作一个角等于已知角
已知：∠AOB．求作：∠A′O′B′=∠AOB．
作法：
（1）以点O 为圆心，任意长为半径画弧，分别交OA，
OB 于点C,D；
（2）画一条射线O′A′，以点O′为圆心，OC 长为半

人教版八年级数学上册教学：12-2 全等三角形的判定(SAS) (共11张)PPT课件

人教版八年级数学上册教学：12-2 全等三角形的判定(SAS) (共11张)PPT课件
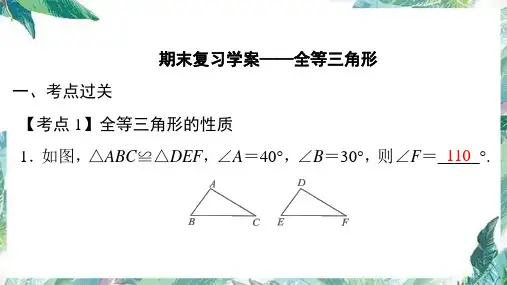
三角形全等的判定定理（SAS）
当两个三角形满足六个条件中的三个时，有四种 情况:
(1) 三个角 不能! (2) 三条边 SSS (3) 两边一角 ?
(4) 两角一边
继续探讨三角形全等的条件： 两边一角
思考：已知一个三角形的两条边和一个角，那么这两条边
与这一个角的位置上有几种可能性呢？
A
A
B
C
图一
图2-39
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ . (3)△ABC和△A’B’C’ 的位置关系如图2-40.
图2-40
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ .
(4)△ABC和△A’B’C’ 的位置关系如图2-41.
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ . (1)△ABC和△A’B’C’ 的位置关系如图2-38.
A’
B’
C’
图2-38
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ . (2)△ABC和△A’B’C’ 的位置关系如图2-39.
Байду номын сангаас证明：在△ACO和△BDO中, AO=BO, ∠AOC=∠BOD（对顶角相等）, CO=DO, ∴△ACO≌△BDO（SAS）.
图2-42
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
11
结束语
当你尽了自己的最大努力时，失 败也是伟大的，所以不要放弃，

人教版初中八年级上册数学-期末复习 第12章全等三角形 课件(共48张PPT)

人教版初中八年级上册数学-期末复习 第12章全等三角形 课件(共48张PPT)
的依据是_H__L_.
第3题
4．如图，AO＝BO，下列条件不能判定△AOD≌△BOC 的是( B )
A．OC＝OD C． ∠A＝∠B
第4题 B．AD＝BC D．∠C＝∠D
【考点 3】角平分线的性质和判定 5．如图，在△ABC 中，∠C＝90°，AD 平分∠BAC，AB＝6，CD
＝2，则点 D 到 AB 的距离是_2_，△ABD 的面积是_6_.
用 HL 证 Rt△ABC≌Rt△DEC. 得 ∠A＝∠D， 从而 AB∥DE.
10．如图，在△ABC 和△DEF 中，下面有四个条件，请你在其中 选 3 个作为题设，余下的 1 个作为结论，写一个真命题，并加 以证明. ① AB＝DE；②AC＝DF；③∠ABC＝∠DEF；④BE ＝CF.
题设：①③④；结论：② 证明提示：BC＝BE＋EC＝CF＋EC＝EF. 用 SAS 证明△ABC≌△DEF，从而 AC＝DF.
证明：(1)如图，连接 AF， ∵Rt△ABC≌Rt△ADE，∴AC＝AE，BC＝DE， ∵∠ACB＝∠AEF＝90°，AF＝AF， ∴Rt△ACF≌Rt△AEF， ∴CF＝EF.∴BF＋EF＝BF＋CF＝BC， ∴BF＋EF＝DE；
(2)如图，DE＝BF－EF，理由是： 连接 AF，∵Rt△ABC≌Rt△ADE， ∴AC＝AE，BC＝DE， ∵∠E＝∠ACF＝90°，AF＝AF， ∴Rt△ACF≌Rt△AEF，∴CF＝EF， ∴DE＝BC＝BF－FC＝BF－EF，即 DE＝BF－EF.
24．已知 Rt△ABC≌Rt△ADE，其中∠ACB＝∠AED＝90°. (1)将这两个三角形按图①方式摆放，使点 E 落在 AB 上，DE 的延长线交 BC 于点 F.求证：BE＋EF＝DE； (2)改变△ADE 的位置，使 DE 交 BC 的延长线于点 F(如图②)， 写出此时 BF、EF 与 DE 之间的等量关系，并说明理由．

人教版八上数学《1三角形全等的判定》课件

人教版八上数学《1三角形全等的判定》课件
三角形全等的判定（1）
复习
1. 三角形全等的性质是什么？
Zx xk
2. 如果两个三角形满足三条边对应相等，三个角对 应相等，那么，这两个三角形全等吗？
3. 如果两个三角形满足上述六个条件中的一部分， 是否也能保证两个三角形全等呢？
探究1
先任意画出一个△ABC，再画 一个△A/B/C/，使△ABC与△A/B/C/ 满足上述六个条件中的一个或两个.
你画出的△A/B/C/与△ABC一定BC，再画 一个△A/B/C/，使A/B/=AB， B/C/ =BC， A/C/ =AC. 把画好的Zx △xk A/B/C/剪下，放 到△ABC上，它们全等吗？
画法
已知：任意 △ ABC，画一个△ A’B’C’，使A’B’ ＝AB，A’C’＝AC，B’C’=BC
练习
已知：点A、E、F、C在同一条直线上， AD=CB，DF=BE，AE=CF.证明△ADF≌△CBE 还应有什么条件？怎样才能得到这个条件？
A E
D
F
B
C
练习
如图，已知点B、E、C、F在同一条直线上，
AB＝DE，AC＝DF，BE＝CF.
求证：∠A＝∠D.
A
D
证明：∵BE＝CF（已知）
∴ BE+EC=CF+EC
A 画法：1. 画线段B’C’=BC.
2. 分别以B’、C’为圆心，
B
A’ C
BA、CA为半径画弧，两弧
相交于点A’.
3. 连接A’B’、A’C’.
B问’ ：通过实验可以发C’现什形△么. A事’实B？’C’就是所要画的三角
规律
探究2反映的规律是： 三条边对应相等的两个三角形全等（简写成“边
边边”或“SSS”）

最新人教版初中数学八年级上册《12.2 三角形全等的判定(第2课时)》精品教学课件

最新人教版初中数学八年级上册《12.2 三角形全等的判定(第2课时)》精品教学课件

∴ ∠A=∠D(全等三角形的对应角相等).
A D C
E
探究新知
素养考点 2 利用全等三角形测距离
例2 如图，有一池塘，要测池塘两端A、B的距离，可先在平
地上取一个可以直接到达A和B的点C，连接AC并延长到点D，
使CD＝CA，连接BC并延长到点E，使CE＝CB．连接DE，
那么量出DE的长就是A、B的距离，为什么?
课堂检测
能力提升题
已知：如图，AB=AC, BD=CD，E为AD上一点.
求证： BE=CE.
证明： 在△ABD和△ACD中，
A
AB=AC (已知），
BD=CD (已知），
AD=AD(公共边）， ∴△ABD≌△ACD（SSS）.
E
∴ ∠BAD=∠CAD，
B DC
在△ABE和△ACE中，
AB=AC (已知），
证明：在△ABC 和△DEC 中，
AC = DC（已知），
A
B
∠ACB =∠DCE （对顶角相等）， CB=EC（已知），
·C
∴△ABC ≌△DEC（SAS）.
E
D
∴AB =DE .（全等三角形的对应边相等）
巩固练习
如图，两车从南北方向的路段AB的A端出发，分别向东、
向西行进相同的距离，到达C，D两地.此时C，D到B的距
三边对应相等的两个三角形全等（可以简写为“边边边”或
“SSS”）.
2.符号语言表达：
A
在△ABC和△ DEF中
AB=DE， BC=EF， CA=FD，
B
D
C
∴ △ABC ≌△ DEF.（SSS）
E
F
探究新知
【思考】除了SSS外,还有其他情况吗？ 当两个三角形满足六个条件中的3个时，有四种情况:

人教版八年级数学上册第十二章全等三角形复习课(共25张PPT)

人教版八年级数学上册第十二章全等三角形复习课(共25张PPT)
【思维模式】在证明线段相等或角相等的题目中，通常通过证明 这两条线段或角所在的三角形全等来得到线段相等或角相等，若这 两条线段或角在不可能全等的两个三角形中，还可寻求题目中的已 知条件或图形中的隐含条件通过等量代换来达到证明全等的目的．
例3： 第一节数学课后，老师布置了一道课后练习：如图，已知在Rt△ABC中 ，AB＝BC，∠ABC＝90°，BO⊥AC于点O．点P，D分别在AO和BC上，PB＝ PD，DE⊥AC于点E．
O，请写出图中一组相等的线段______________．
5． 如图，△ABC≌△DEF，请根据图中提供的信息，写出x＝
_____．
20
AC＝BD或BC＝AD OD＝OC或OA＝OB．
考点3 等腰、等边三角形与全等的综合（考查频率：★★★☆☆） 命题方向：（1）等腰直角三角形与全等三角形的综合问题； （2）等边三角形与全等的综合问题．
D．1cm
例1：如图，AD是等腰直角三角形ABC的底角的平分线，∠C＝ 90°，求证：AB＝AC＋CD．
【思维模式】（1）不管是过点D作AB的垂线也 好，还是延长AC也好，实际上都是利用了角平分 线的轴对称性构造的全等三角形，得出一些相等 的线段或相等的角解决问题；（2）人教课本书 后习题给出了角平分线的另一条性质，即图中 CD∶BD＝AC∶AB，这一结论在解决很多面积有 关问题的时候，也能带来方便．
6． 如图，△ABC和△ECD都是等腰直角三角形，∠ACB＝∠DCE ＝90°，D为AB边上一点．求证：BD＝AE．
考点4 角平分线的性质与判定（考查频率：★★★☆☆） 命题方向：（1）直接考查角平分线基本图形能得到的一些基本结论；（2）角平 分线与其它知识（如中位线、等腰、垂直平分线等）的综合（后面再列举）．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
演讲人：XXXXXX 时 间：XX年XX月XX日
A→∠CAB=∠DAB
例1 ：如图,点B在AE上 ,∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的一 个条件是 ∠∠∠CACCBDB=A=E∠A==∠CD∠.DDBBAE
C
A
B E
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AD=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件
三角形全等 复习课
知识结构图
性质
全等三角形对应边相等 全等三角形对应角相等
全等三角形 全等形
判定 一般三角形 应用
SSS
SAS
直
ASA
角
三
AAS
角
HL
形
解决问题
火眼金睛：
A
AA B
SSA不能 判定全等
BB
CC
DD
B
C A
D
口答
1、如图所示，已知AC=AD,BC=BD, 求证：∠CAB= ∠DAB.
D
∠CBE=∠DBE也可以
(?)
2、证明角、边相等
例（12•区考题第21题）已知如图,点B、F、C、E在同一
1.
直线上， AC、DF相交于G， AB⊥BE，垂足为B ， DE⊥BE，垂足为E， 且AB=DE， BF=CE。
求证（1）△ABC≌△DEF （2）GF=GC
练习
1(2014浙江杭州)在△ABC中，AB＝AC，点E，F 分别在AB，AC上，AE＝AF，BF与CE相交于点P ，求证：PB＝PC，并请直接写出图中其他相等的 线段．
2．如图，在△ABC中，∠ACB=90º， D是AC上 的一点，且AD=BC，DE⊥AC于D， ∠EAB=90º ．求证：AB=AE．
结束语
当你尽了自己的最大努力时，失败也是伟大的， 所以不要放弃，坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End
A
A
E
C
B
翻折
C
B
D
D A
D
A
如：课本P39 第2题
B 课本P41 第1题
DE
CB
C
课本P43 第2题
A
B
CE
如：课本P44 第9题 课本P44 第11题 课本P56 第8题
D
AD
FB
E
C
F
平移
D
A
E
F
B
C
E
A
E
D
A
B
D
C
B
C
如：课本P44 第10题 课本P55 第3题
旋转
主要题型1、添加条件分析：现在我们已知
C
A
B
D
口答
2、如图所示，已知AB=AC,AD=AE, 求证：BE= Hale Waihona Puke D.ADE
B
C
口答
3、如图所示，已知AB∥DE,AC∥DF, BE=CF, 求证：AB= DE.
A
D
B
EC
F
点拨：能用ASA的题目也能用AAS证明。
口答
4、（2013•昆明）已知：如图，AD，BC相 交于点O，OA=OD，AB∥CD． 求证：AB=CD．