新人教版小学数学四年级下册知识点整理

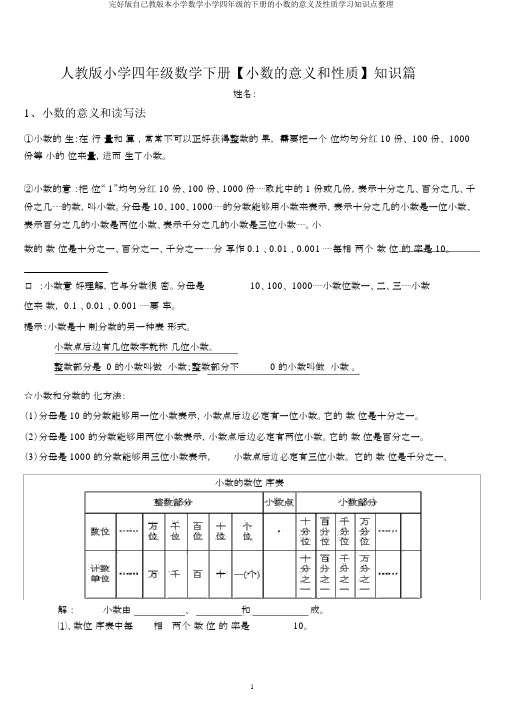
人教版小学四年级数学下册【小数的意义和性质】知识篇姓名：1、小数的意义和读写法①小数的生：在行量和算，常常不可以正好获得整数的果，需要把一个位均匀分红 10 份、 100 份、 1000 份等小的位来量，进而生了小数。

②小数的意：把位“ 1”均匀分红 10 份、100 份、1000 份⋯⋯取此中的 1 份或几份，表示十分之几、百分之几、千份之几⋯⋯的数，叫小数。

分母是 10、100、1000⋯⋯的分数能够用小数来表示，表示十分之几的小数是一位小数、表示百分之几的小数是两位小数、表示千分之几的小数是三位小数⋯⋯。

小数的数位是十分之一、百分之一、千分之一⋯⋯分写作 0.1 、0.01 、0.001 ⋯⋯每相两个数位的率是 10。

口：小数意好理解，它与分数很密。

分母是10、100、 1000⋯⋯小数位数一、二、三⋯⋯小数位来数， 0.1 、0.01 、0.001 ⋯⋯要牢。

提示：小数是十制分数的另一种表形式。

小数点后边有几位数字就称几位小数。

整数部分是 0 的小数叫做小数；整数部分不0 的小数叫做小数。

☆小数和分数的化方法：（1）分母是 10 的分数能够用一位小数表示，小数点后边必定有一位小数。

它的数位是十分之一。

（2）分母是 100 的分数能够用两位小数表示，小数点后边必定有两位小数。

它的数位是百分之一。

（3）分母是 1000 的分数能够用三位小数表示，小数点后边必定有三位小数。

它的数位是千分之一。

小数的数位序表解：小数由、和成。

⑴、数位序表中每相两个数位的率是10。

⑵、小数部分的数位是十分位、百分位、千分位⋯⋯最高位是十分位，没有最低位；整数部分的最低位是个位，没有最高位；个位和十分位的率是 10；没有最大的小数，也没有最小的小数。

整数○小数⑶、没有最大的一位小数，最小的一位小数是0.1 。

例：（1）6.378 的数位是（ 0.001 ）， 6.378 中有（ 6378）个千分之一（ 0.001 ）。

【新人教版】小学数学四年级下册知识点总结1、整数加法（1）把两个数合并成一个数的运算叫做加法。

（2）在加法里，相加的数叫做加数，加得的数叫做和。

加数是部分数，和是总数。

(3)加数+加数=和，一个加数=和－另一个加数2、整数减法(1)已知两个加数的和与其中的一个加数，求另一个加数的运算叫做减法。

(2)在减法里，已知的和叫做被减数，已知的加数叫做减数，未知的加数叫做差。

被减数是总数，减数和差分别是部分数。

(3)加法和减法互为逆运算。

3、整数乘法(1)求几个相同加数的和的简便运算叫做乘法。

(2)在乘法里，相同的加数和相同加数的个数都叫做因数。

相同加数的和叫做积。

(3)在乘法里，0和任何数相乘都得0.(4)1和任何数相乘都的任何数。

(5)一个因数×一个因数 =积；一个因数=积÷另一个因数4、整数除法（1）已知两个因数的积与其中一个因数，求另一个因数的运算叫做除法。

（2）在除法里，已知的积叫做被除数，已知的一个因数叫做除数，所求的因数叫做商。

（3）乘法和除法互为逆运算。

（4）在除法里，0不能做除数。

因为0和任何数相乘都得0，所以任何一个数除以0，均得不到一个确定的商。

（5）被除数÷除数=商，除数=被除数÷商被除数=商×除数。

5、整数加法计算法则相同数位对齐，从低位加起，哪一位上的数相加满十，就向前一位进一。

6、整数减法计算法则相同数位对齐，从低位加起，哪一位上的数不够减，就从它的前一位退一作十，和本位上的数合并在一起，再减。

7.整数乘法计算法则先用一个因数每一位上的数分别去乘另一个因数各个数位上的数，用因数哪一位上的数去乘，乘得的数的末尾就对齐哪一位，然后把各次乘得的数加起来。

7、整数除法计算法则（1）先从被除数的高位除起，除数是几位数，就看被除数的前几位；如果不够除，就多看一位，除到被除数的哪一位，商就写在哪一位的上面。

如果哪一位上不够商1，要补“0”占位。

最新人教版小学四年级数学下册知识点归纳数学知识点总结第一单元：四则运算四则运算包括加法、减法、乘法和除法。

1、加减法的意义和关系加法是把两个数合并成一个数的运算，加数加数得和，和减去一个加数得另一个加数。

减法是已知两个数的和与其中一个加数，求另一个数的运算，被减数减去减数得差，差加上减数得被减数。

加法和减法是互逆运算。

2、乘除法的意义和关系乘法是求几个相同加数的和的简便运算，因数相乘得积，积除以另一个因数得另一个因数。

除法是已知两个因数的积与其中一个因数，求另一个因数的运算，被除数除以除数得商，商乘以除数得被除数。

乘法和除法是互逆运算。

3、关于“0”的运算0不能做除数，任何数除以0都是错误的。

任何数加上0等于原数，任何数减去0等于原数。

被减数等于减数时，差是0；被除数等于除数时，商是1.任何数乘以0等于0，0除以任何非零数都等于0.4、四则运算顺序在没有括号的算式里，如果只有加减法或者只有乘除法，都要从左往右按顺序计算。

在没有括号的算式里，有乘除法和加减法，要先算乘除法，再算加减法。

如果一个算式里有括号，先算小括号里面的，再算中括号里面的，最后算括号外面的。

括号里面的算式计算顺序遵循以上的计算顺序。

第二单元：观察物体1、正确辨认物体的现状从上面、前面、左面观察物体，要正确辨认物体的现状。

2、观察物体的诀窍先数看到几个面，再看它们的排列方式。

画图形时要注意只分上下画数量。

3、不同位置观察同一个物体从不同位置观察同一个物体，所看到的形状有可能一样，也有可能不一样。

4、同位置观察不同一个物体从同位置观察不同一个物体，所看到的形状有可能一样，也有可能不一样。

5、全面认识物体从不同位置观察，才能更全面地认识一个物体。

第三单元：时间、速度、路程和单价时间×速度=路程，路程÷时间=速度，路程÷速度=时间。

单价×数量=总价，总价÷单价=数量，总价÷数量=单价。

新人教版小学数学四年级下册期中知识点复习一、四则运算1、加、减法的意义及各部分之间的关系：⑴把两个数合并成一个数的运算，叫做加法。

⑵已知两个数的和与其中一个加数，求另一个加数的运管，叫做减法加数 + 加数 =和被减数－减数=差和－加数=加数被减数－差 =减数差+减数=被减数2、乘、除法的意义及各部分之间的关系：⑴求几个相同加数的和的简便运算，叫做乘法.⑵已知两个因数的积与其中一个因数，求另一个因数的运管，叫做除法因数× 因数 =积被除数÷除数=商积÷因数=因数被除数÷商=除数商×除数=被除数3、加法、减法、乘法和除法统称四则运算。

4、在没有括号的算式里，如果只有加、减法或者只有乘、除法，都要从左往右按顺序计算。

5、在没有括号的算式里，有乘、除法和加、减法、要先算乘除法，再算加减法。

6、算式有括号，先算括号里面的，再算括号外面的；括号里面的算式计算顺序遵循以上的计算顺序。

二、运算定律及简便运算：一、加法运算定律：1、加法交换律：两个数相加，交换加数的位置，和不变。

a+b=b+a2、加法结合律：三个数相加，可以先把前两个数相加，再加上第三个数；或者先把后两个数相加，再加上第一个数，和不变。

（a+b）+c=a+(b+c) 加法的这两个定律往往结合起来一起使用。

3、连减的性质：一个数连续减去两个数，等于这个数减去那两个数的和。

a-b-c=a-(b+c)二、乘法运算定律：1、乘法交换律：两个数相乘，交换因数的位置，积不变。

a×b=b×a2、乘法结合律：三个数相乘，可以先把前两个数相乘，再乘以第三个数，也可以先把后两个数相乘，再乘以第一个数，积不变。

（a×b ）× c = a× (b×c )乘法的这两个定律往往结合起来一起使用。

3、乘法分配律：两个数的和与一个数相乘，可以先把这两个数分别与这两个数相乘，再把积相加。

新人教版小学数学四年级下册知识点(1—8单元)度而变化的。

3、平行于正面的面叫顶面，平行于底面的面叫底面。

4、长方体和正方体的表面积都可以通过计算各个面的面积再求和得到。

5、长方体和正方体的体积可以通过计算底面积再乘以高得到。

6、观察物体时可以用手绘制出物体的投影图，投影图是物体在一个平面上的影像。

7、投影图有正面投影、侧面投影和俯视图等不同类型。

8、在绘制投影图时需要注意比例关系和投影线的方向，以便准确地表示物体的形状和大小。

3) 乘法分配律是指两个数的和与一个数相乘时，可以先把这两个数分别与这个数相乘，再把积相加。

具体公式为：(a+b)×c=a×c+b×c。

此外，还有其他拓展公式，如(a-b)×c=a×c-b×c，(a±b±c)×m=a×m±b×m±c×m，以及(a+b+c)÷m=a÷m+b÷m+c÷m，(a-b)÷c=a÷c-b÷c，a×c±b×c=(a±b)×c，a÷c±b÷c=(a±b)÷c。

在简算时，需要根据不同的情况选择使用哪种定律。

4、连除的性质有两点。

首先，一个数连续除以两个数，等于除以这两个数的积。

具体公式为：a÷b÷c=a÷(b×c)。

其次，一个数连续除以几个数，任意交换除数的位置，商不变。

具体公式为：a÷b÷c÷d=a÷d÷b÷c。

5、在简算中，需要注意一些易错的情况，比如0.6+0.4-0.6+0.438×99+99.此外，还需要掌握小数的意义和性质。

小数是在进行测量和计算时，不能正好得到整数的结果时使用的表示方法。

第一单元《四则运算》知识点总结及典型易错题详解1、加、减的意义和各部分间的关系（1）把两个数合并成一个数的运算，叫做（加法）。

（2）相加的两个数叫做（加数）。

加得的数叫做（和）。

（3）已知两个数的和与其中的一个加数，求（另一个加数）的运算，叫做（减法）。

（4）在减法中，已知的和叫做被减数，减法是加法的（逆运算）。

2、乘、除法的意义和各部分间的关系（1）求几个相同加数的和和的简便运算，叫做（乘法）。

（2）相乘的两个数叫做（因数）。

乘得的数叫做（积）。

（3）已知两个因数的积与其中一个因数，求（另一个因数）的运算，叫做（除法）。

（4）在除法中，已知的积叫做（被除数），除法是乘法的（逆运算）。

3、加法各部分的关系：加数+加数=和加数=和-另一个加数减法各部分的关系：被减数-减数=差被减数-差=减数差+减数=被减数乘法各部分间的关系：因数×因数=积因数=积÷另一个因数除法各部分间的关系：被除数÷除数=商除数=被除数÷商被除数＝商×除数有余数的除法：被除数=商×除数+余数除数=（被除数-余数）÷商商=（被除数-余数）÷除数/4、四则混和运算的顺序（1）在没有括号的算式里，如果只有加、减法，或者只有乘、除法，都要按（从左往右）的顺序计算；（2）在没有括号的算式里，如果既有乘、除法，又有加、减法，要先算（乘、除法），后算（加、减法）；（先乘除，后加减）；（3）在有括号的算式里，要先算（括号里面）的，后算（括号外面）的。

5、有关0的计算①一个数和0相加，结果还得原数：a＋0=（a）0＋（a）=a②一个数减去0，结果还得这个数：a-0=（a）③一个数减去它自己，结果得零：a-a=（0）④一个数和0相乘，结果得0：a×0=（0）；（0）×a=0⑤0除以一个非0的数，结果得0：0÷a=（0）⑥0不能做（除数）：a÷0=（无意义）6、租船问题。

最新人教版小学四年级数学全册知识点汇总毫米面积单位：平方千米、公顷、亩、平方米、平方分米、平方厘米进率：长度单位之间进率为10，面积单位之间进率为100二、公顷和平方千米的认识1、公顷是面积单位，1公顷等于10万平方米。

2、平方千米是面积单位，1平方千米等于100万平方米。

3、公顷和平方千米常用于表示土地面积、国家面积等。

三、换算1、将公顷换算成平方千米，需要将公顷数除以10.2、将平方千米换算成公顷，需要将平方千米数乘以10.四、应用1、在解决土地面积问题时，需要了解和掌握公顷和平方千米的换算方法。

2、在研究地图时，需要了解和掌握不同面积单位的换算方法，以便更好地理解地图上的比例尺。

五、计算工具的认识1、算盘是我国古代发明的计算工具，至今仍在使用。

2、算盘的上珠代表5，下珠代表1.3、计算器是现代常用的计算工具，具有开关、清除等功能键。

掌握计算器的使用方法可以提高计算效率。

进率：1千米=1000米，1米=10分米=100厘米，1分米=10厘米。

面积单位有平方千米、公顷、平方米、平方分米、平方厘米。

进率：1平方千米=100公顷=xxxxxxx平方米，1公顷=平方米，1平方米=100平方分米=平方厘米，1平方分米=100平方厘米。

在带面积单位时，先考虑面积的大小，再看括号前面数的大小。

例如，果园、广场、体育馆一般带公顷，如一个足球场的面积大约是1公顷，而一个果园的面积是3公顷。

较大的面积如一个区、一个城市、一个省、一个国家都用平方千米做单位，如洛阳市的面积约为平方千米，河南省的面积约为17万平方千米，上海市的面积约为6364平方千米。

射出来的光线像手电筒、汽车灯和太阳等可以近似地看成射线。

射线有一个端点，没有端点的那一端可以无限延伸。

不能量出长度，因此出现一条射线长8米这样的判断题一定是错的。

读作：射线AB（只有一种读法，从端点读起）。

把线段的一端无限延长，就得到一条射线。

把线段的两端都无限延长，就得到一条直线。

②除以几个数的积就等于连续除以这几个数。

6.乘、除混合的简便计算：第一个数的位置不变，其余的因数、除数可以交换位置。

（可以先乘，也可以先除）例如：27×13÷9=27÷9×13四、连除的性质：一个数连续除以两个数，等于除以这两个数的积。

a÷b÷c = a÷(b×c)1、常见乘法计算：25×4＝100 125×8＝10002、加法交换律简算例子：3、加法结合律简算例子：50＋98 ＋50 488 ＋40＋60＝50 ＋50 ＋98 ＝488 ＋（40 ＋60）＝100＋98 ＝488＋100＝198 ＝5884、乘法交换律简算例子：5、乘法结合律简算例子：25×56×4 99×125×8＝25×4×56 ＝99×（125×8）＝100×56 ＝99×1000＝5600 ＝990006、含有加法交换律与结合律的简便计算：65＋28＋35 ＋72＝（65＋35）＋（28 ＋72）＝100 100＝2007、含有乘法交换律与结合律的简便计算：25×125×4×8＝（25×4）×（125×8）＝100×1000＝100000乘法分配律简算例子：1、分解式2、合并式25×（40 4）135×12—135×2＝25×40 25×4 ＝135×（12—2）＝1000 100 ＝135×10＝1100 ＝13503、特殊14、特殊23、小数是十进制分数的另一种表现形式。

4、小数的计数单位是十分之一、百分之一、千分之一……分别写作0.1、0.01、0.001……5、每相邻两个计数单位间的进率是10。

人教版小学四年级数学下册【小数的意义和性质】知识篇姓名：1、小数的意义和读写法①小数的产生：在进行测量和计算时，往往不能正好得到整数的结果，还需要把一个单位平均分成10 份、100 份、1000 份等较小的单位来量，从而产生了小数。

②小数的意义：把单位“ 1”平均分成10 份、100份、1000份⋯⋯取其中的1 份或几份，表示十分之几、百分之几、千份之几⋯⋯的数，叫小数。

分母是10、100、1000⋯⋯的分数可以用小数来表示，表示十分之几的小数是一位小数、表示百分之几的小数是两位小数、表示千分之几的小数是三位小数⋯⋯。

小数的计数单位是十分之一、百分之一、千分之一⋯⋯分别写作0.1 、0.01 、0.001 ⋯⋯每相邻两个计数单位间的进率是10。

口诀：小数意义好理解，它与分数很亲密。

分母是10、100、1000⋯⋯小数位数一、二、三⋯⋯小数单位来计数，0.1 、0.01 、0.001 ⋯⋯要记牢。

提醒：小数是十进制分数的另一种表现形式。

小数点后面有几位数字就称为几位小数。

整数部分是0的小数叫做纯小数；整数部分不为0的小数叫做带小数。

☆小数和分数的转化方法：（1）分母是10 的分数可以用一位小数表示，小数点后面一定有一位小数。

它的计数单位是十分之一。

（2）分母是100 的分数可以用两位小数表示，小数点后面一定有两位小数。

它的计数单位是百分之一。

（3）分母是1000 的分数可以用三位小数表示，小数点后面一定有三位小数。

它的计数单位是千分之一。

小数的数位顺序表解读：小数由、和组成。

⑴、数位顺序表中每相邻两个计数单位间的进率是10。

⑵、小数部分的数位是十分位、百分位、千分位⋯⋯最高位是十分位，没有最低位；整数部分的最低位是个位，没有最高位；个位和十分位的进率是10；没有最大的小数，也没有最小的小数。

整数○小数⑶、没有最大的一位小数，最小的一位小数是0.1举例：（1）6.378 的计数单位是（0.001 ），6.378 中有（6378）个千分之一（0.001 ）。