第三章 静定结构的受力分析(龙驭球第三版3.8)
- 格式:docx
- 大小:93.54 KB
- 文档页数:3

目 录第一部分 名校考研真题第1章 绪 论第2章 结构的几何构造分析第3章 静定结构的受力分析第4章 影响线第二部分 课后习题第1章 绪 论第2章 结构的几何构造分析第3章 静定结构的受力分析第4章 影响线第三部分 章节题库第1章 绪 论第2章 结构的几何构造分析第3章 静定结构的受力分析第4章 影响线第四部分 模拟试题龙驭球《结构力学Ⅰ》(第3版)配套模拟试题及详解第一部分 名校考研真题第1章 绪 论本章不是考研复习重点,暂未编选名校考研真题,若有最新真题会在下一版中及时更新。
第2章 结构的几何构造分析一、判断题图2-1所示体系的几何组成为几何不变体系,无多余约束。
( )[厦门大学2011研]图2-1二、选择题1.图2-2所示平面体系的几何组成是( )。
[浙江大学2010研]A .几何不变,无多余约束 B .几何不变,有多余约束C .几何常变D.几何瞬变图2-2图2-3错【答案】如图2-1(b ),分别视ABD 和基础为刚片Ⅰ和Ⅱ,两刚片通过链杆AC 、BE 和D 处的支座链杆相连,三根链杆相交于一点O ,故该体系为几何瞬变体系。
【解析】A【答案】如图2-3所示,把大地看成刚片3,刚片1和2形成瞬铰(1,2),刚片1和3形成瞬铰(1,3),刚片2和3形成无穷远处瞬铰(2,3),三个铰不共线,因此是无多余约束的几何不变体系。
【解析】2.图2-4(a )所示体系的几何组成是( )。
[武汉大学2012研、郑州大学2010研、华南理工大学2007研、河海大学2007研]A .无多余约束的几何不变体系B .几何可变体系C .有多余约束的几何不变体系D.瞬变体系图2-4三、填空题1.图2-5所示体系是几何________变体系,有________个多余约束。
[重庆大学2006研]图2-52.如图2-6(a )所示体系的几何组成为________体系。
[南京理工大学2011研]图2-6A【答案】鉴于刚片与构件可以等效互换,所以可将图2-4(a )所示体系替换为图2-4(b )所示体系,然后通过依次去除C 支座链杆与CE 杆、D 支座链杆与DE 杆所组成的二元体,以及二元体A-E-B 后,可知原体系为无多余约束的几何不变体系。

第三章静定结构的受力分析一、基本概念1.静定结构的分类静定结构按其几何组成的特点,可分为两刚片结构、三刚片结构和主从结构(由基本部分和附属部分组成)。
按受力特性不同可分为梁、拱、刚架、桁架和组合结构。
2.静定结构的分析方法用截面法取隔离体,用平衡条件求支座反力和内力。
3.静定结构的特点(1)用静力平衡条件可求得全部反力和内力,且解唯一。
(2)仅在荷载作用下产生内力。
其他因素作用时,只引起位移,不产生内力。
(3)平衡力系作用在静定结构的某一内部几何不变部分时,只有此部分产生内力。
(4)作用在静定结构某一内部几何不变部分上的荷载,在该部分作等效变换时,仅该部分内力发生变化而其余部分内力保持不变。
★静定结构的性质(1)静定结构是无多余约束的几何不变体系,用静力平衡条件可以唯一地求得全部内力和反力。
(2)静定结构只在荷载作用下产生内力,其他因素作用时(如支座位移,温度变化、制造误差等),只引起位移和变形(应变),不产生内力。
(3)静定结构的内力与杆件的刚度无关。
(4)在荷载作用下,如果仅靠静定结构的某一局部就可以与荷载维持平衡,则只有这部分受力,其余部分不受力。
(5)当静定结构的一个内部几何不变部分上的荷载作等效变换时,其余部分的内力不变。
(6)当静定结构的一个内部几何不变部分作构造变换时,其余部分的内力不变。
(7)作用在基本部分的荷载不引起附属部分的内力,而作用在附属部分的荷载在基本部分上则产生内力。
二、静定梁和静定刚架内力分析1.叠加原理及适用条件叠加原理可表述为:结构中由一组荷载(外力、温度变化、支座沉陷等)产生的内力或位移等于每一荷载单独作用产生的内力或位移的总和。
叠加原理用于静定结构内力计算时,应满足的条件为小变形;用于位移计算和超静定结构内力计算时,材料还应服从虎克定律。
2.截面法的应用(1)内力符号规定轴力以拉力为正;剪力以绕隔离体顺时针转动为正,正剪力绘于梁的上侧或柱的左侧;弯矩不规定正负,绘于杆件的受拉侧。



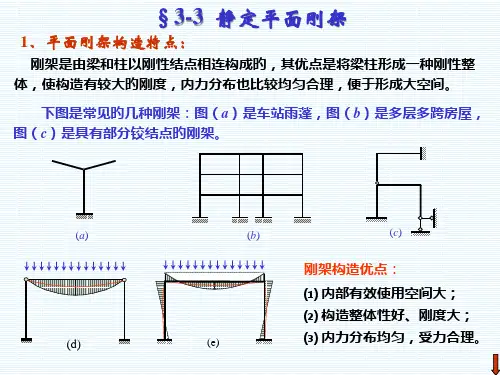

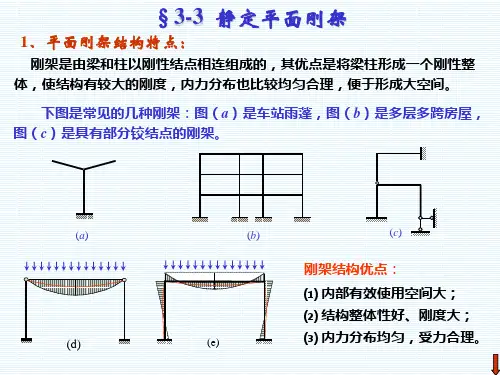



§3-8 刚体体系的虚功原理
计算静定结构内力的另一个普遍方法—虚功原理,它等价于平衡方程。
虚功的概念:
力与沿力作用点方向上的位移的乘积。
虚功中的力和位移之间没有因果关系。
这是虚功区别于实功的重要特点。
虚功可大于零也可小于零。
一、刚体体系的虚功原理
设刚体体系上作用任意的平衡力系,又设体系发生符合约束的无限小刚体位移,则主动力在位移上所作的虚功总和恒等于零。
刚体体系的虚功方程:
W 外虚=0
由于虚功中的力与位移没有因果关系,可使其中的一种状态是虚设的,而另一种是真实的状态。
因此,虚功方程演变出两种形式及应用:
两种应用:
虚设位移—虚位移原理求静定结构内力。
虚设力系—虚力原理求刚体体系的位移。
虚位移原理的应用
体系上真实的平衡力系,虚设体系的无限小刚体位移,外力所作的总虚功等于零。
虚位移方程用于求真实的未知力(内力、支座反力)。
例:
虚功方程为
0)(P P =∆-+∆F F X X
几何关系:
a
b X P =∆∆ 则P F a
b F X =
或设 1=∆X
相应的虚功方程为
01P =⎪⎭⎫ ⎝
⎛⋅-+⋅a b F F X
则P F a
b F X 二、应用虚功原理求静定结构的支反力
图(a)为一静定梁,拟求支座A 的反力F X 。
结论:撤除与F X 相应的约束,结构变成机构,约束力变成主动力,机构可能发生的刚体体系位移当作虚位移,写出虚功方程确定几何关系,求F X 。
例3-16 试求图示静定多跨梁在C 点的支座反力F X 。
设荷载F P1 和F P2 等于常数F P 。
三、应用虚功原理求静定结构的内力
例3-17 试求简支梁截面C 的弯矩M C 。
例3-18 试求图示简支梁截面C 的剪力F Q C 。