2011习题与思考题

思考题与习题第2章 水文学的一般概念与水文测验2.1 如何量取河长?如何计量某河段的弯曲系数？ 2.2 简述平原河道平面形态特点与水流冲淤特性。

2.3如题2.3表，已知各河段特征点的河底高程及其间距，试求各河段的平均比降及 全河的平均比降。

2.4 什么叫流域分水线?如何量取流域面积？2.5 河川径流一般指的是什么?河川径流量可用哪几个特征值表示？2.6某河某水文站控制流域面积为566km 2,多年平均径流量为8.8m 3 / s ,多年平均降雨量为686.7mm ,试求其各径流特征值。

河段平均比降计算资料题2.3表2.7 我国南、北方河流的特征时期是什么？ 2.8 影响径流的主要因素有哪些？2.9什么叫水位?如何测定水尺的零点高程？2.10 简述如何用流速仪测量流速并计算流量。

2.11 含沙量与输沙率有何不同？ 2.12已测得13对水位一流量关系如题2.12表1所示，另有实测的水位一面积、水位一水面宽度以及用流速仪测得的4个水位一流量关系如题2.12表2所示。

试用断面特征法 将水位一流量关系曲线延长到最高水位H =4.0m 处。

实测水位一流量关系题2.12表1第三章水文统计基本原理与方法3.1 水文计算为什么要采用数理统计法？3.2 频率、概率和累积频率有什么区别?扼要说明累积频率的基本特性。

3.3 什么叫重现期?它和物理学中的周期有何区别？ 3.4 累积频率与设计频率有何区别？ 3.5 简述经验适线法的操作步骤。

3.6 试述计算经验频率曲线及理论频率曲线的意义。

3.7 设有系列：1, 2, 3, 4, 5, 6, 20,试求此系列的统计参数。

3.8有A , B 两系列，A 系列平均数为弓，偏态系数C s A ,对应的累积频率为P A ； B 系列平均数为，偏态系数为C s B , B 对应的累积频率为P B 。

若C s A >C s B ,试分析P A 与 P B 哪个大（扼要说明原因）？3.9已知统计参数Q =1000m 3/s , C v =0.5, C s =2C v ,试绘制理论频率曲线，并确定P =1%时的设计流量Q 设。

第一章习题与思考题1、常见的金属晶格类型有哪些?试绘图说明其特征。

2、实际金属中有哪些晶体缺陷?晶体缺陷对金属的性能有何影响?3、为什么单晶体具有各向异性，而多晶体在一般情况下不显示各向异性？4、试计算面心立方晶格的致密度。

5、什么是位错？位错密度的大小对金属强度有何影响？6、晶体在结晶时，晶核形成种类有几种？什么是变质处理？7、置换固溶体中，被置换的溶剂原子哪里去了？8、间隙固溶体和间隙化合物在晶体结构与性能上区别何在？举例说明之。

9、解释下列名词：晶格、晶胞、晶体、晶面、晶向、晶粒、点缺陷、面缺陷、线缺陷、相、固溶强化、金属化合物、固溶体第二章习题与思考题1、什么叫结晶、过冷现象、过冷度?过冷度与冷却速度有何关系?2、金属的晶粒大小对力学性能有何影响?控制金属晶粒大小的方法有哪些?3、如果其它条件相同，试比较下列铸造条件下，铸件晶粒的大小：（1）金属型浇注与砂型浇注；（2）浇注温度高与浇注温度低；（3）铸成薄壁件与铸成厚壁件；（4）厚大铸件的表面部分与中心部分；（5）浇注时采用振动与不采用振动。

4、金属铸锭通常由哪几个晶区组成？它们的组织和性能有何特点？第三章习题与思考题1、现有A、B两元素组成如图3.1所示的二元匀晶相图，试分析以下几种说法是否正确？为什么？（1）形成二元匀晶相图的A与B两个相元的晶格类型可以不同，但是原子大小一定相等。

（2）K合金结晶过程中，由于固相成分随固相线变化，故已结晶出来的固溶体中含B量总是高于原液相中含B量。

（3）固溶体合金按匀晶相图进行结晶时，由于不同温度下结晶出来的固溶体成分和剩余液相成分都不相同，故在平衡状态下固溶体的成分是不均匀的。

图3.1 题1 图2、共晶部分的Mg-Cu相图如图3.2所示：（1）填入各区域的组织组成物和相组成物。

在各区域中是否会有纯Mg相存在？为什么？（2）求出20%Cu合金冷却到500℃、400℃时各相的成分和重量百分比。

（3）画出20%Cu合金自液相冷到室温的却曲线，并注明各阶段的相与相变过程。

2011年全国各地高考数学试题及解答分类汇编大全（07数系的扩充与复数的引入）一、选择题：1. (2011安徽文、理)设 i 是虚数单位，复数ai i1+2-为纯虚数，则实数a 为（ ） （A ）2 (B) -2 (C) 1-2 (D) 121.A 【解析】本题主要考察复数的乘法运算和复数的概念。

法一：()()()()()ai i ai a a i i i i 1+2+1+2-+2+1==2-2-2+5g 为纯虚数，所以,a a 2-=0=2； 法二：()i a i ai i i-1+=2-2-为纯虚数，所以a =2，答案为A. 法三： 设()ai bi b R i1+∈2-=，则1+(2)2ai bi i b bi =-=+，所以1,2b a ==.故选A. 【技巧点拨】复数运算乘法是本质，除法中的分母“实化”也是乘法，同时注意提取公因式，因式分解等变形技巧的运用。

2. (2011北京文、理)复数212i i-=+ ( ) (A)i (B )i - (C)4355i -- (D)4355i -+ 2.【答案】A2.【解析】：22i 2(i 2)(12i)2242(1)2412i (12i)(12i)1414(1)i i i i i i i ---------+====++----，选A 。

3. (2011福建理) i 是虚数单位，若集合S=}{1.0.1-，则（ ） A.i S ∈ B.2i S ∈ C. 3i S ∈ D.2S i ∈ 3.解析：由21i S =-∈得选项B 正确。

4. (2011福建文) i 是虚数单位1+i 3等于（ ）A.iB.-iC.1+i D .1-i4. 解析：1+i 3=1-I ，答案应选D 。

5．(2011广东文)设复数z 满足1iz =，其中i 为虚数单位，则z =（ ）A ．i -B ．iC ．1-D ．15. 解析：（A ）．1()i z i i i i -===-⨯-6．(2011广东理)设复数z 满足(1)2i z +=，其中i 为虚数单位，则z =（ ）A ．1i +B ．1i -C ．22i +D ．22i -解析：（B ）．22(1)11(1)(1)i z i i i i -===-++-7. (2011湖北理)i 为虚数单位，则=⎪⎭⎫⎝⎛-+201111i i （ ）A.i -B.1-C.iD.17.【答案】A7. 解析：因为()i i i i i =-+=-+221111，所以i i i i i i -====⎪⎭⎫ ⎝⎛-++⨯3350242011201111，故选A .8．(2011湖南文、理)若,,a b R i ∈为虚数单位，且()a i i b i +=+，则（ ）Ａ．1,1a b == Ｂ．1,1a b =-= Ｃ．1,1a b ==- Ｄ．1,1a b =-=-8.答案：C8. 解析：因()1a i i ai b i +=-+=+，根据复数相等的条件可知1,1a b ==-。

2011年全国各地高考数学试题及解答分类汇编大全（14统计、统计案例、算法初步、框图、推理与证明）一、选择题：1. (2011北京文)执行如图所示的程序框图，若输入A 的值为2，则输出的P 值为( )(A)2 (B)3 (C)4 (D)51.【答案】C【解析】执行三次循环，12S A =≤=成立，112p =+=，1131122S P =+=+=，322S A =≤=成立，213p =+=，3131112236S P =+=+=，1126S A =≤=成立，314p =+=1111112566412S p =+=+=，25212S A =≤=不成立，输出4p =，故选C2.(2011北京理)执行如图所示的程序框图，输出的s 值为（ ）（A ）-3 （B ）-12（C ）13 （D ）22.【答案】D【解析】：循环操作4次时S 的值分别为11,,3,232--，选D 。

3. (2011福建文)某校选修乒乓球课程的学生中，高一年级有30名， 高二年级有40名。

现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为（ ）A. 6B. 8C. 10D.12解析：由30:406:,n =可得8n =，答案应选B 。

4. (2011福建文)阅读右图所示的程序框图，运行相应的程序，输出的结果是（ ）A.3B.11C.38D.1234.解析：110,12310,a a =<=+=<2321110,11a a =+=>=,答案应选B 。

5. (2011广东理) 设S 是整数集Z 的非空子集，如果S b a ∈∀,,有S ab ∈,则称S 关于数的乘法是封闭的，若T,V 是Z 的两个不相交的非空子集，T ∪V=Z, 且T c b a ∈∀,,,有T c ab ∈,;V z y x ∈∀,,,有V xyz ∈,则下列结论恒成立的是（ ）A. T,V 中至少有一个关于乘法是封闭的B. T,V 中至多有一个关于乘法是封闭的C. T,V 中有且只有一个关于乘法是封闭的D. T,V 中每一个关于乘法是封闭的5. 解析：（A ）．若T 为奇数集，V 为偶数集，满足题意，此时T 与V 关于乘法都是封闭的，排除B 、C ，若T 为负整数集，V 为非负整数集，也满足题意，此时只有V 关于乘法是封闭的，排除D 。

2011物质结构基础复习思考题物质结构基础复习题⼀、填空题1、Li 2分⼦按分⼦轨道理论表⽰的电⼦排布为222*121s s s σσσ，说明（答“有或⽆”）有 Li 2分⼦存在。

2、固溶体按溶质原⼦分布有⽆规律可分为有序固溶体和⽆序固溶体。

3、铺展是固、⽓界⾯变为液、⽓界⾯和固、液界⾯的过程。

4、根据分⼦轨道理论解释He 2分⼦不存在，是因为He 2分⼦的电⼦排布式为2*121s s σσ。

5、固体中的转变类型有四种，其中有序程度变化的是⾮晶态的晶化和结构驰豫，化学成分变化的是相分离，晶体结构变化的是同素异构转变。

6、共价键的特点是具有⽅向性和饱和性。

7、晶体中原⼦排列的紧密程度是反映晶体结构特征的⼀个重要因素。

为了定量地表⽰原⼦排列的紧密程度，通常应⽤配位数和致密度这两个参数。

8、反应扩散是指是随扩散原⼦增多超过基体固溶体溶解度极限⽽形成新相的扩散 .9、元素的电负性是指元素的原⼦在分⼦中吸引电⼦的能⼒，在周期表中，同⼀周期元素的电负性由左向右逐渐增⼤，⽽同⼀族元素的负电性由上到下逐渐减⼩。

⼆元合⾦中两组元的电负性差越⼤，越易形成形成的化合物，越不易形成（置换）固溶体。

10、⾦属典型的晶体结构类型有FCC 、BCC 和HCP ，其配位数相应为12、8、12；晶胞中原⼦数相应为4、2、6。

11低浓度⽅向进⾏，在此过程中扩散驱动⼒是化学位梯度（化学势梯度、化学⼒）。

12、刃型位错既可以作滑移运动，也可以作攀移运动，螺型位错只能作滑移运动，因为它没有多余的半原⼦⾯。

13、合⾦结晶过程中，形核时既需要结构（相起伏）起伏和能量起伏，⼜需要成分起伏。

14、⾦属结晶的过程是不断形核和长⼤的过程。

15、三元合⾦中两相平衡时，合⾦的成分点和两个平衡相的成分点，必须在同⼀直线上。

⼆、判断题（正确的打√，错误的打×）1、相变时新旧两相的化学势相等，化学势的⼀级偏微商也相等的相变称为⼀级相变。

×2、包晶转变是指由液相与⼀个固相相互作⽤，包覆原有固相形成的另⼀个新固相的转变。

第11章 供配电系统的运行和管理11-1．节约电能有何重要意义？答：节约电能的意义主要表现为：1．缓解电力供需矛盾。

节约电能可以节约煤炭、水力、石油等一次能源，使整个能源资源得到合理使用，缓解电力供需矛盾,并能减轻能源部门和交通运输部门的紧张程度。

2．节约国家的基建投资。

节约电能可以节约国家用于发电、输配电及用电设备所需要的投资，给整个国民经济带来很大的利益,有利于国民经济的发展。

3．提高企业的经济效益。

节约电能可以减少企业的电费开支，降低生产成本，积累资金，提高企业的经济效益。

4．推动企业用电合理化。

节约电能可以推动企业采用新技术、新材料、新设备、新工艺，加速设备改造和工艺改革，从而提高企业的经营管理水平，使企业生产能力得到充分发挥，促进企业生产水平的不断发展和提高。

11-2．什么叫负荷调整？有哪些主要调整措施？答：根据供电系统的电能供应情况及各类用户不同的用电规律，合理地安排各类用户的用点时间，以降低负荷高峰，填补负荷的低谷（即所谓的“削峰填谷”），充分发挥发、变电设备的潜能，提高系统的供电能力。

负荷调整的主要措施：①同一地区各厂的厂休日错开；②同一厂内各车间的上下班时间错开，使各个车间的高峰负荷分散；③调整大容量用电设备的用点时间，使它避开高峰负荷时间用电，做到各时段负荷均衡，从而提高了变压器的负荷系数和功率因数，减少电能的损耗。

④实行“阶梯电价+分时电价” 的综合电价模式。

“阶梯电价”全名为“阶梯式累进电价”，是指把户均用电量设置为若干个阶梯，随着户均消费电量的增长，电价逐级递增。

峰谷分时电价是指根据电网的负荷变化情况，将每天24小时划分为高峰、平段、低谷等时段，各时段电价不同，以鼓励用电客户合理安排用电时间，削峰填谷，提高电力资源的利用效率。

11-3．什么叫经济运行？什么叫变压器的经济负荷？答：经济运行是指整个电力系统的有功损耗最小，获得最佳经济效益的设备运行方式。

变压器的经济负荷S ec.T ，就是应满足变压器单位容量的综合有功损耗△P/S 为最小值的条件。

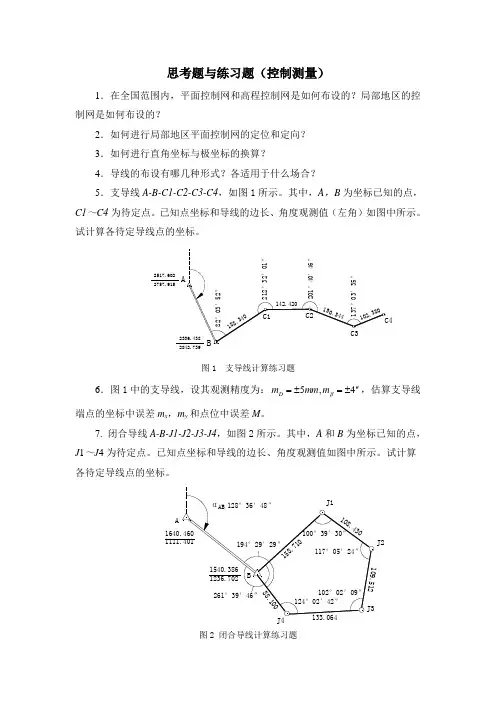
思考题与练习题（控制测量）1．在全国范围内，平面控制网和高程控制网是如何布设的？局部地区的控制网是如何布设的？2．如何进行局部地区平面控制网的定位和定向？ 3．如何进行直角坐标与极坐标的换算？4．导线的布设有哪几种形式？各适用于什么场合？5．支导线A-B-C1-C2-C3-C4，如图1所示。

其中，A ，B 为坐标已知的点，C1～C4为待定点。

已知点坐标和导线的边长、角度观测值（左角）如图中所示。

试计算各待定导线点的坐标。

图1 支导线计算练习题6．图1中的支导线，设其观测精度为：4,5''±=±=βm mm m D ，估算支导线端点的坐标中误差m x ，m y 和点位中误差M 。

7. 闭合导线A-B-J1-J2-J3-J4，如图2所示。

其中，A 和B 为坐标已知的点，J 1～J 4为待定点。

已知点坐标和导线的边长、角度观测值如图中所示。

试计算各待定导线点的坐标。

J2图2 闭合导线计算练习题8. 附合导线A-B-K1-K2-K3-C-D ，如图3所示。

其中A ，B ，C ，D 为坐标已知的点，K 1～K 3为待定点。

已知点坐标和导线的边长、角度观测值如图中所示。

试计算各待定导线点的坐标。

CDA1708.1171355.584图3 附合导线计算练习题9．无定向B-T1-T2-T3-T4-C 如图4所示。

其中B 和C 为坐标已知的点，T1～T4为待定点。

已知点坐标和导线的边长、角度观测值如图中所示。

试计算各待定导线点的坐标。

179°12′10″193°13′24″2367.8732407.7521673.4502230.880B图4 无定向导线计算练习题10．用测角交会测定P 点的位置。

已知点A ，B 的坐标和观测的交会角α，β如图5所示，计算P 点的坐标。

BP图5 测角交会计算练习题11．用测边交会测定P 点的位置。

已知点A ，B 的坐标和观测的边长a ，b 如图6所示，计算P 点的坐标。

2011年高考（浙江理）一、选择题 1 ．设函数2(0)()(0)x x f x x x -≤⎧=⎨>⎩,若)(αf =4,则实数α= （ ）A ．4-或2-B ．4-或2C ．2-或4D ．2-或22 ．把复数z 的共轭复数记作z ,i 为虚数单位.若1z i =+,则(1)z z +⋅=（ ）A ．i -3B ．i +3C ．i 31+D ．3 3 ．若某几何体的三视图如图所示,则这个几何体的直观图可以是4 ．下列命题中错误的是（ ）A ．如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βB ．如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC ．如果平面α⊥平面γ,平面β⊥平面γ,l αβ= ,那么l ⊥平面γD ．如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β5 ．设实数x 、y 是不等式组2502700,0x y x y x y +->⎧⎪+->⎨⎪≥≥⎩,若x 、y 为整数,则34x y +的最小值为（ ）A ．14B ．16C ．17D ．196 ．若02πα<<,02πβ-<<,1cos()43πα+=,cos()42πβ-=,则cos ()2βα+= （ ）A B ．C D ．7 ．若a 、b 为实数,则“01ab <<”是“1a b <或1b a>”的 （ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件8 ．已知椭圆22122:1x y C a b +=(a >b >0)与双曲线222:14y C x -=有公共的焦点,2C 的一条正视图侧视图俯视图(A)(B) (C) (D)渐近线与以1C 的长轴为直径的圆相交于,A B 两点. 若1C 恰好将线段AB 三等分,则 （ ）A ．232a =B ．213a =C ．212b =D ．22b =9 ．有5本不同的书,其中语文书2本,数学书2本,物理书1本.若将其随机地摆放在书架的同一层上,则同一科目的书都不相邻的概率是 （ ）A ．15B ．25C ．53 D ．4510．设,,a b c 为实数,22()()(),()(1)(1)f x x a x bx c g x ax cx bx =+++=+++.记集合},0)(|{R x x f x S ∈==,},0)(|{R x x g x T ∈==. 若||,||S T 分别为集合,S T 的元素个数,则下列结论不可能．．．的是 （ ）A ．||1S =且||0T =B ．||1S =且||1T =C ．||2S =且||2T =D ．||2S =且||3T =二、填空题 11．若函数2()||f x x x a =-+为偶函数,则实数a = ______12．若某程序框图如图所示,则该程序运行后输出的k 值为 _______。

第一章复习思考题与练习题：一、思考题1．统计的基本任务是什么？2．统计研究的基本方法有哪些？3．如何理解统计总体的基本特征。

4．试述统计总体和总体单位的关系。

5．标志与指标有何区别何联系。

二、判断题1、社会经济统计的研究对象是社会经济现象总体的各个方面。

（）2、在全国工业普查中，全国企业数是统计总体，每个工业企业是总体单位。

（）3、总体单位是标志的承担者，标志是依附于单位的。

（）4、数量指标是由数量标志汇总来的，质量指标是由品质标志汇总来的。

（）5、全面调查和非全面调查是根据调查结果所得的资料是否全面来划分的（）。

三、单项选择题1、社会经济统计的研究对象是（）。

A、抽象的数量关系B、社会经济现象的规律性C、社会经济现象的数量特征和数量关系D、社会经济统计认识过程的规律和方法2、某城市工业企业未安装设备普查，总体单位是（）。

A、工业企业全部未安装设备B、工业企业每一台未安装设备C、每个工业企业的未安装设备D、每一个工业3、标志是说明总体单位特征的名称，标志有数量标志和品质标志，因此（）。

A、标志值有两大类：品质标志值和数量标志值B、品质标志才有标志值C、数量标志才有标志值D、品质标志和数量标志都具有标志值4、统计规律性主要是通过运用下述方法经整理、分析后得出的结论（）。

A、统计分组法B、大量观察法C、综合指标法D、统计推断法5、指标是说明总体特征的，标志是说明总体单位特征的，所以（）。

A、标志和指标之间的关系是固定不变的B、标志和指标之间的关系是可以变化的C、标志和指标都是可以用数值表示的D、只有指标才可以用数值表示答案：二、 1.× 2.× 3.√ 4.× 5.×三、 1.C 2.B 3.C 4.B 5.B第四章一、复习思考题1.什么是平均指标？平均指标可以分为哪些种类？2．为什么说平均数反映了总体分布的集中趋势？3．为什么说简单算术平均数是加权算术平均数的特例？4．算术平均数的数学性质有哪些？5．众数和中位数分别有哪些特点？6.什么是标志变动度？标志变动度的作用是什么？7.标志变动度可分为哪些指标？它们分别是如何运用的？8.平均数与标志变动度为什么要结合运用？二、练习题要求：试用次数权数计算该村居民平均月收入水平。

正视图 图1 侧视图 图2俯视图 图32011年普通高等学校招生全国统一考试（广东卷）数学（理科）一、选择题：本大题共8小题，每小题5分，满分40分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设复数z 满足(1)2i z +=，其中i 为虚数单位，则z =A ．1i +B ．1i -C ．22i +D ．22i -2．已知集合{(,)|,A x y x y =为实数，且221}x y +=，{(,)|,B x y x y =为实数，且}y x =，则A B⋂的元素个数为A ．0B ．1C ．2D ．3 3．若向量,,a b c 满足a ∥b 且⊥a c ，则(2)⋅+=c a bA ．4B ．3C ．2D ．0 4．设函数()f x 和()g x 分别是R 上的偶函数和奇函数，则下列结论恒成立的是A ．()()f x g x +是偶函数B ．()()f x g x -是奇函数C ．()()f x g x +是偶函数D ．()()fx g x -是奇函数5．已知平面直角坐标系xOy 上的区域D 由不等式组02x y x ⎧⎪⎨⎪⎩≤≤≤≤给定．若(,)M x y 为D 上的动点，点A 的坐标为，则z OM OA=⋅的最大值为A． B ． C ．4 D ．36．甲、乙两队进行排球决赛，现在的情形是甲队只要再赢一局就获冠军，乙队需要再赢两局才能得冠军．若两队胜每局的概率相同，则甲队获得冠军的概率为A ．12B ．35C ．23D ．347．如图1 ~ 3的正视图（主视侧视图（左视矩形，则该几何体的体积为图4COPBAA ．B ．C ．D ．8．设S 是整数集Z 的非空子集，如果,a b S ∀∈，有ab S ∈，则称S 关于数的乘法是封闭的．若,T V 是Z 的两个不相交的非空子集，T V Z ⋃=，且,,a b c T ∀∈，有abc T ∈；,,x y z V ∀∈，有xyz V ∈，则下列结论恒成立的是A ．,T V 中至少有一个关于乘法是封闭的B ．,T V 中至多有一个关于乘法是封闭的C ．,T V 中有且只有一个关于乘法是封闭的D ．,T V 中每一个关于乘法都是封闭的 二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分． （一）必做题（9 ~ 13题）9．不等式13x x +--≥0的解集是 ． 10．72()x x x-的展开式中，4x 的系数是 （用数字作答）11．等差数列{}n a 前9项的和等于前4项的和．若11a =，40k a a +=，则k = ． 12．函数32()31f x x x =-+在x = 处取得极小值．13．某数学老师身高176cm ，他爷爷、父亲和儿子的身高分别是173cm 、170cm 和182cm ．因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为 cm ． 14．（坐标系与参数方程选做题）已知两曲线参数方程分别为sin x y θθ⎧=⎪⎨=⎪⎩(0)θπ<≤和254x t y t ⎧=⎪⎨⎪=⎩(t ∈)R ，它们的交点坐标为___________．15．（几何证明选讲选做题）如图4，过圆O 外一点P 分别作 圆的切线和割线交圆于,A B ，且7P B =，C 是圆上一点使得5B C =，BAC APB ∠=∠，则A B =___________．图5CDPBAEF三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）已知函数1()2sin()36f x x π=-，x ∈R ．（1）求5()4f π的值；（2）设,0,2παβ⎡⎤∈⎢⎥⎣⎦，10(3)213f πα+=，6(32)5f βπ+=，求cos()αβ+的值．17．（本小题满分13分）为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件，测量产品中微量元素,x y 的含量（单位：毫克）．下表是乙厂的5件产品的测量数据：（1）已知甲厂生产的产品共有98件，求乙厂生产的产品数量；（2）当产品中的微量元素,x y 满足175x ≥且75y ≥时，该产品为优等品．用上述样本数据估计乙厂生产的优等品的数量；（3）从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数ξ的分布列及其均值（即数学期望）．18．（本小题满分13分）如图5，在锥体P A BC D -中，A B C D 是边长为1的 菱形，且60DAB ∠=，PA PD ==2PB =，,E F分别是B C ,PC 的中点．（1）证明：AD ⊥平面DE F ； （2）求二面角P AD B --的余弦值． 19．（本小题满分14分）设圆C 与两圆22(4x y ++=，22(4x y -+=中的一个内切，另一个外切．（1）求C 的圆心轨迹L 的方程； （2）已知点55M ，0)F ，且P 为L 上动点，求M P FP - 的最大值及此时点P的坐标．20．（本小题满分14分）设0b >，数列{}n a 满足1a b =，1122n n n nba a a n --=+-(2)n ≥．（1）求数列{}n a 的通项公式；（2）证明：对于一切正整数n ，1112n n n b a ++≤+．21．（本小题满分14分）在平面直角坐标系xOy 上，给定抛物线L ：214y x =．实数,p q 满足24p q -≥0，12,x x 是方程20x px q -+=的两根，记12(,)max{,}p q x x ϕ=．（1）过点2001(,)4A p p 0(0)p ≠作L 的切线交y 轴于点B ．证明：对线段A B 上的任一点(,)Q p q ，有0(,)2p p q ϕ=；（2）设(,)M a b 是定点，其中,a b 满足240a b ->，0a ≠．过(,)M a b 作L 的两条切线12,l l ，切点分别为2111(,)4E p p ，2221(,)4E p p '，12,l l 与y 轴分别交于,F F '．线段E F 上异于两端点的点集记为X ．证明：112(,)(,)2p M a b X p p a b ϕ∈⇔>⇔=；（3）设{(,)|D x y y =≤1x -，y ≥215(1)}44x +-．当点(,)p q 取遍D 时，求(,)p q ϕ的最小值 （记为m in ϕ）和最大值（记为max ϕ）参考答案 1．（B ）．22(1)11(1)(1)i z i ii i -===-++-2．（C ）．A B ⋂的元素个数等价于圆221x y +=与直线y x =的交点个数，显然有2个交点 3．（D ）．依题意得⊥c a ，⊥c b ，则(2)20⋅+=⋅+⋅=c a b c a c b4．（A ）．由()f x 是偶函数、()g x 是奇函数，得()f x 和()g x 都是偶函数，所以()()f x g x +与()()f x g x -都是偶函数，()()f x g x +与()()f x g x -的奇偶性不能确定5．（C ）．z y =+，即y z =-+，画出不等式组表示的平面区域，易知当直线y z =+经过点2)时，z取得最大值，max 24z ==6．（D ）．乙获得冠军的概率为111224⨯=，则甲队获得冠军的概率为13144-=7．（B ）．该几何体是一个底面为平行四边形，高为3，则33V Sh ==⨯=8．（A ）．若T 为奇数集，V 为偶数集，满足题意，此时T 与V 关于乘法都是封闭的，排除B 、C 若T 为负整数集，V 为非负整数集，也满足题意，此时只有V 关于乘法是封闭的，排除D 9．[1,)+∞．解析：13x x +--≥0 ⇒1x +≥3x -⇒2(1)x +≥2(3)x -⇒x ≥1 10．84．解析：72()x x x-的通项7821772()(2)r rr r r rr T x C x C xx--+=-=-，由824r -=得2r =，则227(2)84C -=11．10．方法1：由94S S =得93646d d +=+，求得16d =-，则4111(1)()13()066k a a k +=+-⨯-++⨯-=，解得10k =方法2：由94S S =得567890a a a a a ++++=，即750a =，70a =，即104720a a a +==，即10k =12．2．解析：2()363(2)f x x x x x '=-=-，令()0f x '=得0x =或2x =，显然当0x <时()0f x '>；当02x <<时()0f x '<；当2x >时()0f x '>，函数32()31f x x x =-+在2x =处取得极小值 13．185．设父亲的身高为x cm ，儿子的身高为y cm ，则根据上述数据可得到如下表格：上表中的最后一组(182,?)是预测数据，173,176x y ==12221()()00361033()nii i ni i xx yy bx x ==--++⨯===++-∑∑， 3ay b x =-= 线性回归方程 3y x =+，所以当182x =时，185y =，即他孙子的预测身高为185 cm ． 14．(1,5．sin x y θθ⎧=⎪⎨=⎪⎩表示椭圆2215x y +=(01)x y <≤≤≤，254x t y t⎧=⎪⎨⎪=⎩表示抛物线245y x =22221(01)5450145x y x y x x x y x ⎧+=<≤≤≤⎪⎪⇒+-=⇒=⎨⎪=⎪⎩或5x =-（舍去）， 又因为01y ≤≤，所以它们的交点坐标为(1,515P A B A C B ∠=∠，又B A C A P B ∠=∠，则△P A B ∽△AC B ，则P BA BA B B C=，235AB PB BC =⋅=，即AB =16．解：（1）515()2sin()2sin 43464f ππππ=⨯-==（2）110(3)2sin[(3)]2sin 232613f πππααα+=+-==，即5sin 13α= 16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=，即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦，∴12cos 13α==，4sin 5β==∴1235416cos()cos cos sin sin 13513565αβαβαβ+=-=⨯-⨯=17．解：（1）设乙厂生产的产品数量为a 件，则98145a =，解得35a =所以乙厂生产的产品数量为35件（2）从乙厂抽取的5件产品中，编号为2、5的产品是优等品，即5件产品中有2件是优等品由此可以估算出乙厂生产的优等品的数量为235145⨯=（件）（3）ξ可能的取值为0，1，223253(0),10C P C ξ===1123256(1),10C C P C ξ===22251(2),10C P C ξ===∴ξ的分布列为：CDPBAE FH∴3614012.1010105E ξ=⨯+⨯+⨯=18．（1）证明：取A D 的中点H ，连接,,PH BH BD∵PA PD =，∴AD PH ⊥∵在边长为1的菱形A B C D 中，60DAB ∠= ∴△ABD 是等边三角形∴AD H B ⊥，PH HB H = ∴AD ⊥平面PH B ∴AD PB ⊥∵,E F 分别是B C ,PC 的中点∴E F ∥P B ，H B ∥D E ∴AD D E ⊥，AD EF ⊥，DE EF E = ∴AD ⊥平面D E F（2）解：由（1）知PH AD ⊥，HB AD ⊥∴P H B ∠是二面角P AD B --的平面角，易求得22PH BH ==∴2227334cos 27222PH H B PBPH B PH HB+--+-∠====-⋅∴二面角P AD B--的余弦值为7-19．解：（1）设(0),0)F F '，圆C 的半径为r ，则(2)(2)4CF CF r r '-=+--=< ∴C 的圆心轨迹L 是以,F F '为焦点的双曲线，2a =，c =，1b =∴C 的圆心轨迹L 的方程为2214xy -=（2）2M P FP M F -≤== ∴M P FP - 如图所示，P 必在L 直线M F 的斜率2k =-:2M F y x =-+22142x y y x ⎧-=⎪⎨⎪=-+⎩215280x -+=，6)0--=，12155x x ==∵P x >5P x =5P y =-∴M P FP - 的最大值为2，此时P为55-20．（1）解：∵1122n n n nba a a n --=+-∴1122n n n a ba n a n --=+-∴1211nn n n a b a b --=⋅+ ① 当2b =时，1112nn n n a a ---=，则{}nn a 是以12为首项，12为公差的等差数列∴11(1)22nn n a =+-⨯，即2n a =② 当0b >且2b ≠时，11211()22nn n n a b b a b--+=+-- 当1n =时，122(2)nn a bb b +=--∴1{}2nn a b +-是以2(2)b b -为首项，2b为公比的等比数列∴112()22nnn a bb b +=⋅--∴212(2)2(2)nn nn nnn ba b b b b b -=-=---∴(2)2nn nnn b b a b-=-综上所述(2),02222nn n n n b b b b a b b ⎧->≠⎪=-⎨⎪=⎩　且， （2）方法一：证明：① 当2b =时，11122n n n b a ++=+=；② 当0b >且2b ≠时，12212(2)(222)n n n n n n b b b bb -----=-++++1221222nnnn n n n n n ba b bb----⋅=≤=++++1112111111222222222n nn n n n n n n n bb b b+++----+++=====<=⋅1112n n b +++∴对于一切正整数n ，1112n n n b a ++≤+．方法二：证明：① 当2b =时，11122n n n b a ++=+=；② 当0b >且2b ≠时， 要证1112n n n b a ++≤+，只需证11(2)122nn nnn nb b b b++-≤+-，即证1(2)122nnn nn b b bb+-≤+-即证1221112222n n n n n nnb b b bb----+≤+++++即证122111()(222)2n n n n n nb b bbn b----++++++≥即证2112231122221()()2222n nn n nn nn b b bb n bbbb---+-+++++++++≥∵2112231122221()()2222n nn n nn nn b b bb bbbb---+-+++++++++2121232111222()()()()2222n n nn nn n nb b bb bbbb----+=++++++++n ≥+= ，∴原不等式成立∴对于一切正整数n ，1112n n n b a ++≤+．21．解：（1）2001(,)4A p p 是抛物线L 上的点，12y x '=，则切线的斜率012k p = 过点A 的抛物线L 的切线方程为A B ：200011()42y p p x p -=-，即2001124y p x p =-∵(,)Q p q 在线段A B 上，∴2001124q p p p =-，∴22220001144()()24p q p p p p p p -=--=-≥0不妨设方程20x px q -+=的两根为12x =，22x =则012p p p x --=，022p p p x +-=① 当00p >时，00p p ≤≤，001222p p p x p -==-，022p x =∵00122p p x -<≤，∴12x x ≤，∴122(,)max{,}p q x x x ϕ==02p =② 当00p <时，00p p ≤≤，012p x =，002222p p p x p -==-∵00222p p x ≤<-，∴12x x ≥，∴121(,)max{,}p q x x x ϕ==02p =综上所述，对线段A B 上的任一点(,)Q p q ，有0(,)2p p q ϕ=（2）由（1）知抛物线L 在2001(,)4p p 处的切线方程为2001124y p x p =-，即200240p p x y -+=∵切线恒过点(,)M a b ，则200240p ap b -+=，∴1,2p a =±① 当0a >时，(,)M a b X ∈⇔10a p <<⇔1p a =+，2p a =-⇔12p p >② 当0a <时，(,)M a b X ∈⇔10p a <<⇔1p a =-2p a =+⇔12p p >综合①②可得(,)M a b X ∈⇔12p p >∵由（1）可知，若2111(,)4E p p ，点(,)M a b 在线段E F 上，有1(,)2p a b ϕ=∴(,)M a b X ∈⇒1(,)2p a b ϕ=③由（1）可知，方程20x a x b -+=的两根11,22p x =或12p a -，21,22p x =或22p a -若1(,)2p a b ϕ=，即112max{,}2p x x = 则1122p a p -≥、2122p p ≥、2122p a p -≥∴12p p >∴1(,)2p a b ϕ=⇒12||||p p >⇒(,)M a b X ∈ ④综合③④可得(,)M a b X ∈⇔1(,)2p a b ϕ=综上所述112(,)(,)2p M a b X p p a b ϕ∈⇔>⇔=；（3）由2115(1)44y x y x =-⎧⎪⎨=+-⎪⎩，求得两个交点(0,1),(2,1)-，则02p ≤≤， 过点(,)G p q 作抛物线L 的切线，设切点为N 2001(,)4x x ，切线与y 轴的交点为H由（2）知200240x px q -+=，解得0x p =±，①若0x p =+(,)G p q 在线段N H 上，由1y x ≤-，得1q p ≤-，∴022x p p p p =+≥+=+-=，∴0m min in )12(x ϕ==．由215(1)44y x ≥+-，得221511(1)14442q p p p ≥+-=+-∴2442p q p -≤-，∴0x p p =+≤+令t =，则2122p t =-+，02t ≤≤∴22011552(1)2222x t t t ≤-++=--+≤∴0max max 5)24(x ϕ==②若0x p =-，则点(,)G p q 在线段N H 的延长线上方程20x px q -+=的两根为012p p x x --=，022p p x x +-=即01,22x x =或02x p -∵0x p ≤∴00012(,)max{,}max{,}222x x x p q x x p p ϕ==-=-2p -==51(,)4p q ϕ≤≤综上所述m in 1ϕ=，m ax 54ϕ=。

2011年普通高等学校招生全国统一考试（新课标卷）解析版文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3至4页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。

请认真核准条形码上的准考证号、姓名和科目。

2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动， 用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效。

3．第Ⅰ卷共l2小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合{}{}0,1,2,3,4,1,3,5,,M N P M N === 则P 的子集共有（A ）2个 （B ）4个 （C ）6个 （D ）8个解析：本题考查交集和子集概念，属于容易题。

显然P={}3,1，子集数为22=4 故选B（2）复数512ii=-（A ）2i - （B ）12i - （C ）2i -+ （D ）12i -+ 解析：本题考查复数的运算，属容易题。

解法一：直接法512ii=-()()()ii i i i +-=+-+22121215，故选C解法二：验证法 验证每个选项与1-2i 的积，正好等于5i 的便是答案。

（3）下列函数中，即是偶数又在()0,+∞单调递增的函数是A.3y x= B.1y x =+ C. 21y x =-+ D.2xy -=解析：本题考查函数的奇偶性和单调性，属于简单题 可以直接判断：A 是奇函数，B 是偶函数，又是()0,+∞的增函数，故选B 。

(4).椭圆221168xy+=的离心率为A. 13 B. 12C. 3D. 2解析;本题考查椭圆离心率的概念，属于容易题，直接求e=22422==ac,故选D 。

第四章 思考题与习题解答1. 解释以下名词术语：滴定分析法，滴定，标准溶液（滴定剂），标定，化学计量点，滴定终点，滴定误差，指示剂，基准物质。

答：滴定分析法：将已知准确浓度的标准溶液滴加到被测物质的溶液中，或者将被测溶液滴加到标准溶液中，直到两者按化学计量关系定量反应为止，然后根据标准溶液的浓度和所消耗的体积，计算出被测物质的含量。

这种定量分析方法称为滴定分析法。

滴定：滴定分析中，把滴定剂通过滴定管逐滴滴加到锥形瓶内待测物质溶液中的操作过程称为滴定。

标准溶液（滴定剂）：已知其准确浓度，用于滴定分析的溶液称为标准溶液。

标定：通过滴定确定溶液准确浓度的操作过程称为标定。

化学计量点：滴定分析中，当标准溶液与被测物质的反应恰好定量完成时，称反应到达了化学计量点。

滴定终点：滴定分析中，指示剂的变色点称为滴定终点。

滴定误差：滴定终点与化学计量点不一致，而引起的分析误差称为滴定误差，又称终点误差。

指示剂：通过颜色的改变来指示滴定终点的试剂。

基准物质：可用于直接配制标准溶液或标定标准溶液准确浓度的物质。

2. 滴定度的表示方法T B/A 和T B/A %各自的意义如何？答：A B T 是指每毫升标准溶液相当于被测物质的质量（g 或mg ）。

%A B T 是指表示每毫升标准溶液相当于被测物质的质量分数。

3. 基准试剂（1）H 2C 2O 4 ·2H 2O 因保存不当而部分风化；（2）Na 2CO 3因吸潮带有少量湿存水。

用（1）标定NaOH[或用（2）标定HC1]溶液的浓度时，结果是偏高还是偏低？用此NaOH （HC1）溶液测定某有机酸（有机碱）的摩尔质量时结果偏高还是偏低？答： （１）用部分风化的H 2C 2O 4·2H 2O 作为基准试剂标定NaOH 溶液的浓度时，所消耗NaOH 物质的量（真实值）将比理论计算值增多。

此时如仍按较小的理论计算值（H 2C 2O 4 ·2H 2O 完全不风化时应消耗的NaOH 的量）进行计算，则有NaOH c （名义值）Vn NaOH )(理论值=所得（名义值）必然较真实值偏低，即产生负误差。

2011年天河区初中毕业班综合练习（数学）参考答案说明：1、本解答给出了一种解法供参考，如果考生的解法与本解答不同，各题组可根据试题的主要考查内容比照评分标准制订相应的评分细则．2、对于计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3、解答右端所注分数，表示考生正确做到这一步应得的累加分数． 一、选择题（本题共10小题，每小题3分，共30分）三、解答题（本题有9个小题, 共102分。

解答应写出文字说明、证明过程或演算步骤） 17.（本题满分9分）一天晚上,小明帮助姐姐清洗两套只有颜色不同的有盖茶杯，此时突然停电了，小明只好把杯盖和茶杯随机地搭配在一起，用列表法或树形图法求颜色搭配正确的概率是多少？ 解：如图：-------------5分所以颜色搭配正确的概率P=2142= ---------------9分（2分+2分） （注明：该步骤中只写P 12=，只给2分） 18.（本题满分9分）若m 满足式子322m m +>，试判断关于x 的一元二次方程240x x m -+=的根的情况. 解： 2(4)4164m m =--=- --------2分由322m m +>，解得4m < --------5分∴1640m -> 即0> --------7分∴方程240x x m -+=有两个不相等实数根. --------9分 19.（本题满分10分）如图，AB 是⊙O 的直径，且AB =4，AC 是弦，∠CAB =40°，求劣弧BC 和弦AC 的长. （弧长计算结果保留π，AB弦长精确到0.01）解：∵∠ACB =40°∴∠A0B =80°--------2分∴240281809BClππ⨯⨯==--------5分 连结BC ，则∠ACB =90°--------7分 在Rt △ACB 中，cos 40=4AC AC AB=∴4cos 4040.766 3.06AC ==⨯≈--------10分另解：过点O 作OE ⊥AC ，垂足为E2AC AE =分在Rt △AEO 中，cos 40=2AE AE AO=∴24cos 4040.766 3.06AC AE ===⨯≈--------10分 20.（本题满分10分）广州市天河区某楼盘准备以每平方米35000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望．为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米28350元的均价开盘销售．（1）求平均每次下调的百分率；（2）某人准备以开盘均价购买一套80平方米的房子．开发商还给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，送两年物业管理费．物业管理费是每平方米每月4元．请问哪种方案更优惠？ 解：（1）设平均每次降价的百分率是x ，依题意得 ---------1分35000（1－x ）2= 28350 ---------------------4分 解得：x 1=10％ x 2＝1910（不合题意，舍去） ---------------6分 答：平均每次降价的百分率为10％． ------------------------7分（2）方案①的房款是：28350×80×0.98＝2222640（元） -------------------8分方案②的房款是：28350×80－4×80×12×2＝2260320（元）---------------9分 ∵2222640＜2260320∴选方案①更优惠． -------------------------10分21.（本题满分12分）如图，等腰△OBD 中，OD=BD ，△OBD 绕点O 逆时针旋转一定角度后得到△OAC ，此时正好B 、D 、C 在同一直线上，且点D 是BC 的中点. （1）求△OBD 旋转的角度； （2）求证：四边形ODAC 是菱形.B B解：（1）∵OD=BD，CD=BD，∴OD=CD=BD------------------1分又△OBD≌△OAC∴OD=OC---------------2分△ODC是等边三角形∴∠COD=60°---------------4分即△OBD旋转的角度为60°---------------5分（2）∵△OBD≌△OAC，△ODC是等边三角形∴OD=OC，BD=AC，OB=OA∠OCA=∠ODB=180°－60°=120°-----------------7分∴∠ACD=∠OCA－∠OCD=120°－60°=60°∴△ACD是等边三角形---------------9分∴OD=OC=AC=AD ---------------11分∴四边形ODAC是菱形. ---------------12分另解：连结AB，由（1）得：∠AOB=60°又OB=OA∴△AOB是等边三角形∴OB=AB---------------7分∴OD=OC=BD=AC∴BC垂直平分OA∴OD= AD --------------9分∴OD=OC=AC=AD ---------------11分∴四边形ODAC是菱形. ---------------12分22.（本题满分12分）如图，在平面直角坐标系中，坐标原点为O，直线l与y轴交点坐标为D（0，8.5），在y轴上有一点B（0，4），请过点B作BA⊥l，交直线l于点A.（1）请在所给的图中画出直线BA，并写出点A的坐标；（2）试求出直线BA解析式，并求出直线BA、直线l与两坐标轴围成的四边形的面积.解：（1）作图，-----------2分（没有直角号扣1分）由图可知：点A的坐标（6，4）-----------3分（2）设直线BA解析式为y kx b=+直线BA过点（6，4）和（0，－4），得：464k bb=+⎧⎨=-⎩-----------4分解得：434kb⎧=⎪⎨⎪=-⎩-----------6分BFE∴直线BA 解析式为443y x =------------7分 设直线BA 与x 轴交于点C ，则点C 的坐标（3，0）-----------8分 连结OA,过A 作AE ⊥x ，AF ⊥y ，垂足分别为E,F 则有8.5,6,3,4OD AF OC AE ==== -------9分直线BA 、直线l 与两坐标轴围成的四边形OCAD 的面积1122OAD OCAS SSOD AF OC AE =+=∙+∙ =11638.5634222⨯⨯+⨯⨯=-----------12分 此问有几种解法，类似给分。

出版专业基础第一章出版概论1.什么是出版？它有哪些构成要素？其前提是什么？出版，是指编辑、复制作品并向公众发行的活动，以传播科学文化、信息和进行思想交流的一种社会活动。

要素：编辑、复制、发行。

进行出版活动还必须具备一个前提——作品。

2.出版活动有哪些特征？文化的记载、传播、交流和传承；不同劳动的有机组合；意识形态属性；经济属性和产业属性。

3.社会发展对出版活动有什么影响？体现在哪些方面？社会的政治状况主导着出版活动的方向：一是通过对出版从业者思想倾向和政治追求的影响来引导出版活动；二是运用行政、法律、法规和政策等手段规制和引导出版活动。

社会经济的发展为出版活动提供物质条件：社会经济的发展是为了满足人们的物质需求。

只有当社会经济发展到一定程度时，才会产生出版活动；只有当社会经济有充分充分的发展时，才会造就巨大的出版物市场。

科学技术是出版活动发展的强大推动力：科学技术不但通过对社会经济的推进积极影响出版活动的发展，而且还通过对出版技术的不断改进，直接促成出版改革的发生和出版业的发展。

社会文化的发展为出版活动提供活力：社会文化发展水平高，出版活动的水平也高。

历史的文化积淀和现实的文化需求所形成的合理，是出版活动最重要的活力和动力。

4.出版活动对社会发展有什么作用？体现在哪些方面？出版活动对社会发展的能动作用。

体现：对政治发展的影响：形成舆论导向；深化思想政治教育；促进社会和谐。

对经济发展的影响：提高劳动力素质，促进社会生产力发展；传递各种社会信息，加快经济的发展速度。

对科学技术的影响：出版活动对科学技术的推进作用，主要在于发现先进科学技术成果并组织、促进其迅速传播，使它们尽快变成现实的生产力。

对文化发展的影响：增进文化积累；推进文化创新；促进文化交流。

5.我国出版工作的指导思想是什么？“以马克思列宁主义、毛泽东思想和邓小平理论和‘三个代表’重要思想为指导，以科学发展观为统领，牢牢把握社会主义先进文化的前进方向，紧紧围绕实现全面建设小康社会宏伟目标和构建社会主义和谐社会的要求，弘扬以爱国主义为核心的民族精神和以改革创新为核心的时代精神，树立新的文化发展观，解放思想、实事求是、开拓创新，发展面向现代化、面向世界、面向未来的民族的科学的大众的社会主义文化，不断满足人民群众日益增长的精神文化需求，努力培育有理想、有道德、有文化、有纪律的社会主义公民，提高全民族的思想道德和科学文化素质，促进人的全面发展和社会全面进步。