下载文档原格式
第一章概论第1题某公共汽车站停放两辆公共汽车A 和B ，从t=1秒开始，每隔1秒有一乘客到达车站。
如果每一乘客以概率21登上A 车，以概率21登上B 车，各乘客登哪一辆车是相互统计独立的，并用j ξ代表t=j 时乘客登上A 车的状态，即乘客登上A 车则j ξ＝1，乘客登上B 车则jξ＝0，则,21}0{,21}1{====j j P P ξξ当t ＝n 时在A 车上的乘客数为n n j j n ηξη,1∑==是一个二项式分布的计算过程。
（1）求n η的概率，即;,...,2,1,0?}{n k k P n ===η（2）当公共汽车A 上到达10个乘客时，A 即开车（例如t ＝21时921=η，且t ＝22时又有一个乘客乘A 车，则t ＝22时A 车出发），求A 车的出发时间n 的概率分布。
解（1）：nn k n k P ⎟⎠⎞⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛==21}{η 解（2）：nn n n P P ⎟⎠⎞⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛−=⎟⎠⎞⎜⎝⎛⎟⎠⎞⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛−==−2191212191A)10n 9A 1-n (}n A {1名乘客登上车时刻第名乘客；在有时刻，车在开车在时刻车第2题设有一采用脉宽调制以传递信息的简单通信系统。
脉冲的重复周期为T ，每一个周期传递一个值；脉冲宽度受到随机信息的调制，使每个脉冲的宽度均匀分布于（0，T ）内，而且不同周期的脉宽是相互统计独立的随机变量；脉冲的幅度为常数A 。
也就是说，这个通信系统传送的信号为随机脉宽等幅度的周期信号，它是以随机过程)(t ξ。
图题1－2画出了它的样本函数。
试求)(t ξ的一维概率密度)(x f t ξ。
解：00(1)()()(){()}{()0}[(1),],(0,){()}{[(1),]}{[(1)]}1(1)(1)1({()0}1{()}t A A n n n Tt n T f x P x A P x P t A P P t P t n T nT n T P t A P t n T nT P t n T d TT t n T T nT t T t n Tt n T T t n P t P t A ξδδξξηξηηηξξ−−=−+====∈−∈==∈−+=>−−=−+−=−==−−−=−−−==−==∫是任意的脉冲宽度01)(1)()()()()(1)()t A T tn T Tf x P x A P x t t n x A n x T T ξδδδδ=−−∴=−+⎛⎞⎛⎞=−−+−−⎜⎟⎜⎟⎝⎠⎝⎠第3题设有一随机过程)(t ξ，它的样本函数为周期性的锯齿波。
随机过程习题解答第一章习题解答1．设随机变量X 服从几何分布，即：(),0,1,2,kP X k pqk ===。
求X 的特征函数，EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtk k X k f t E ee pq ∞===∑ =()1jt k jtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑（其中 0(1)nnnn n n nx n x x ∞∞∞====+-∑∑∑）令 0()(1)nn S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰同理 2(1)2kkkk k k k k kx k x kx x ∞∞∞∞=====+--∑∑∑∑令2()(1)kk S x k x ∞==+∑ 则211()(1)(1)xkk kk k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰）2、（1） 求参数为(,)p b 的Γ分布的特征函数，其概率密度函数为（2） 其期望和方差；（3）证明对具有相同的参数的b 的Γ分布，关于参数p 具有可加性。
解 （1）设X 服从(,)p b Γ分布，则 （2）'1()(0)Xp E X fjb∴==（4）若(,)i i X p b Γ 1,2i = 则同理可得：()()i i P X b f t b jt∑=∑-3、设ln (),()(kZ F X E Zk =并求是常数）。
X 是一随机变量，()F x 是其分布函数，且是严格单调的，求以下随机变量的特征函数。
（1）(),(0,)Y aF X b a b =+≠是常数； （2）ln (),()(kZ F X E Z k =并求是常数）。
解（1）11{()}{()}[()]P F x y P x F y F F y y --<=<==（01y ≤≤） ∴00()0111y F y yy y <⎧⎪=≤≤⎨⎪>⎩∴()F x 在区间[0，1]上服从均匀分布()F x ∴的特征函数为11001()(1)jtx jtx jt X e f t e dx e jt jt ===-⎰ （2）ln ()()()[]jtz jt F x Z f t E e E e ===1ln 01jt ye dy ⋅⎰=111jty dy jt =+⎰4、设12n X X X ，，相互独立，且有相同的几何分布，试求1nkk X =∑的分布。
概率论与随机过程习题答案标准化工作室编码[XX968T-XX89628-XJ668-XT689N]《概率论与随机过程》第一章习题答案1. 写出下列随机试验的样本空间。
（1） 记录一个小班一次数学考试的平均分数（设以百分制记分）。
解： ⎭⎬⎫⎩⎨⎧⨯=n n nn S 100,,1,0 ，其中n 为小班人数。
（2） 同时掷三颗骰子，记录三颗骰子点数之和。
解：{}18,,4,3 =S 。
（3） 10只产品中有3只是次品，每次从其中取一只（取出后不放回），直到将3只次品都取出，记录抽取的次数。
解： {}10,,4,3 =S 。
（4） 生产产品直到得到10件正品，记录生产产品的总件数。
解： {} ,11,10=S 。
（5） 一个小组有A ，B ，C ，D ，E5个人，要选正副小组长各一人（一个人不能兼二个职务），观察选举的结果。
解： {}ED EC EB EA DE DC DB DA CE CD CB CA BE BD BC BA AE AD AC AB S ,,,,,,,,,,,,,,,,,,,=其中，AB 表示A 为正组长，B 为副组长，余类推。
（6） 甲乙二人下棋一局，观察棋赛的结果。
解： {}210,,e e e S =其中，0e 为和棋，1e 为甲胜，2e 为乙胜。
（7） 一口袋中有许多红色、白色、蓝色乒乓球，在其中任意取4只，观察它们具有哪几种颜色。
解： {}rwb wb rb rw b w r S ,,,,,,=其中，,,,b w r 分别表示红色、白色、蓝色。
（8） 对某工厂出厂的产品进行检查，合格的盖上“正品”，不合格的盖上“次品”，如连续查出二个次品就停止检查，或检查4个产品就停止检查，记录检查的结果。
解： {}1111,1110,1101,0111,1011,1010,1100,0110,0101,0100,100,00=S 其中，0为次品，1为正品。
（9） 有A ，B ，C 三只盒子，a ，b ，c 三只球，将三只球装入三只盒子中，使每只盒子装一只球，观察装球的情况。
《概率论与随机过程》第一章习题答案1. 写出下列随机试验的样本空间。
（1） 记录一个小班一次数学考试的平均分数（设以百分制记分）。
解： ⎭⎬⎫⎩⎨⎧⨯=n n nn S 100,,1,0 ，其中n 为小班人数。
（2） 同时掷三颗骰子，记录三颗骰子点数之和。
解：{}18,,4,3 =S 。
（3） 10只产品中有3只是次品，每次从其中取一只（取出后不放回），直到将3只次品都取出，记录抽取的次数。
解： {}10,,4,3 =S 。
（4） 生产产品直到得到10件正品，记录生产产品的总件数。
解： {} ,11,10=S 。
（5） 一个小组有A ，B ，C ，D ，E5个人，要选正副小组长各一人（一个人不能兼二个职务），观察选举的结果。
解： {}ED EC EB EA DE DC DB DA CE CD CB CA BE BD BC BA AE AD AC AB S ,,,,,,,,,,,,,,,,,,,=其中，AB表示A 为正组长，B 为副组长，余类推。
（6） 甲乙二人下棋一局，观察棋赛的结果。
解： {}210,,e e e S =其中，0e 为和棋，1e 为甲胜，2e 为乙胜。
（7） 一口袋中有许多红色、白色、蓝色乒乓球，在其中任意取4只，观察它们具有哪几种颜色。
解： {}rwb wb rb rw b w r S ,,,,,,=其中，,,,b w r 分别表示红色、白色、蓝色。
（8） 对某工厂出厂的产品进行检查，合格的盖上“正品”，不合格的盖上“次品”，如连续查出二个次品就停止检查，或检查4个产品就停止检查，记录检查的结果。
解： {}1111,1110,1101,0111,1011,1010,1100,0110,0101,0100,100,00=S 其中，0为次品，1为正品。
（9） 有A ，B ，C 三只盒子，a ，b ，c 三只球，将三只球装入三只盒子中，使每只盒子装一只球，观察装球的情况。
随机过程作业第一章 P9例题6：随机过程X(t)=A+Bt, t ≥0, 其中A 和B 是独立随机变量，分布服从正态分布N(0, 1)。
求X(t)的一维和二维分布。
解 先求一维分布。
当t 固定，X(t)是随机变量，因为 EX(t)=EA+tEB=0, DX(t)=DA+2t DB=1+2t故X(t)具有正态分布N(0, 1+2t )。
这亦是随机过程X(t)的一维分布。
再求二维分布。
当1t , 2t 固定， X(1t )=A+B 1t , X(2t )=A+B 2t因A 、B 独立同正态分布，故(A, B)T 亦为二维正态分布。
则其线性变换也服从正态分布。
且所以二维分布是数学期望为(0, 0)T,协方差矩阵 的二维正态分布。
P10例题7：随机过程X(t)=Acost, -∞<t<∞,其中A 是随机变量,且有分布列 A 1 2 3 P 1/3 1/3 1/3 求 (1) 一维分布函数(2) 二维分布函数解 (1) 先求所以222211211)DX(t ,1)DX(t , 0)EX(t ,0)(t t t EX +=+===212121211))(())()X(t ())X(t ),(cov(t t Bt A Bt A E t X E t X +=++==⎥⎦⎤⎢⎣⎡++++222121211111t t t t t t )3π,0x x F )2πF(x;x F ;,( ),4;(21π( ;) 4F x π。
X()cos ,442A A ππ==显然，三值，，易知它仅取2232 22{()42P X π=={cos 42P A π==1P{A 1},3==31}223)4({ ,31 }2)4({====ππX P X P 同理，⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≥<≤<≤<= 2 23 x 1,2 23x 2 ,32 2 x 22 ,3122 x 0 )4; ( ，πx F进而有P18例题1：具有随机初相位的简谐波 其中a 与 是正常数，而 服从在区间[0，2 ]上的均匀分布， 求X(t)的数学期望方差和相关函数。
习题11. 令X(t)为二阶矩存在的随机过程，试证它是宽平稳的当且仅当EX(s)与E[X(s)X(s+t)]都不依赖s.证明：充分性：若X(t)为宽平稳的，则由定义知EX(t)=μ， EX(s)X(s+t)=r(t) 均与s 无关必要性：若EX(s)与EX(s)X(s+t)都与s 无关，说明EX(t)=常数， EX(s)X(s+t)为t 的函数2. 记1U ，．．．，n U 为在（０,１）中均匀分布的独立随机变量，对0 < t , x < 1定义I( t , x)=⎩⎨⎧>≤，，，，t x t x 01并记X(t)=),(11∑=nk k U t I n ，10≤≤t ，这是1U ，．．．，n U 的经验分布函数。
试求过程X （t ）的均值和协方差函数。
解： EI ()k U t ,= P ()t U k ≤= t ， D()),(k U t I = EI ()k U t ,－()2),(kU t EI= t －2t = t(1－t)j k ≠， cov ()),(),(j k U s I U t I ，=EI(t,k U )I(s,j U )－EI(t, k U )EI(s, j U ) = st －st=0k = j ， cov ()),(),(j k U s I U t I ，= EI(t,k U )I(s,j U )－st = min(t,s)－stEX(t)=),(11∑=n k k U t EI n =∑=nk tn 11= tcov ())(),(s X t X =()()),(),,(cov 1),(),,(cov 1212j kjk nk k k U s I Ut I n U s I U t I n ∑∑≠=+=[]∑=nk st t s n12),min(1－=()st t s n－),min(13.令1Z ，2Z 为独立的正态分布随机变量，均值为0，方差为2σ，λ为实数，定义过程()t Sin Z t Cos Z t X λλ21+=.试求()t X 的均值函数和协方差函数，它是宽平稳的吗？Solution: ()221,0~,σN Z Z . 02221==EZ EZ .()()221σ==Z D Z D ，()0,21=Z Z Cov ,()0=t EX ，()()()()()[]s Sin Z s Cos Z t Sin Z t Cos Z E s X t X Cov λλλλ2121,+⋅+=[]t C o s S i n Z Z s t S i n C o s Z Z s t S i n S i n Z t C o s C o s Z E λλλλλλλλ12212221+++=()02++=s t S i n S i n s t C o s C o s λλλλσ =()[]λσs t Cos -2(){}t X 为宽平稳过程.4.Poisson 过程()0,≥t t X 满足（i ）()00=X ；(ii)对s t >，()()s X t X -服从均值为()s t -λ的Poisson 分布；（iii ）过程是有独立增量的.试求其均值函数和协方差函数.它是宽平稳的吗？Solution ()()()()t X t X E t EX λ=-=0，()()t t X D λ= ()()()()()s t s X t EX s X t X Cov λλ⋅-=,()()()()()ts s EX s X s X t X E 22λ-+-= ()()()()ts s EX s X D 220λ-++=()ts s s 22λλλ-+=()t s s λλλ-+=1 显然()t X 不是宽平稳的.5. ()t X 为第4题中的Poisson 过程，记()()()t X t X t y -+=1，试求过程()t y 的均值函数和协方差函数，并研究其平稳性. Solution ()λλ=⋅=1t Ey , ()()λ=t y DCov(y(t),y(s))=Ey(t)y(s)-Ey(t)y(s)=E(x(t+1)-x(t))(x(s+1)-x(s))-λ2(1)若s+1<t, 即s≤t-1，则Cov(y(t),y(s))=0-λ2=-λ2(2)若t<s+1≤t+1, 即t>s>t-1, 则Cov(y(t),y(s))=E[x(t+1)-x(s+1)+x(s+1)-x(t)][x(s+1)-x(t)+x(t)-x(s)] -λ2=E(x(t+1)-x(s+1))(x(s+1)-x(t))+E(x(t+1)-x(s+1))(x(t)-x(s))+E(x(s+1)-x(t))+E(x(s+1)-x(t))(x(t)-x(s))- λ2=λ(s+1-t)= λ-λ(t-s)- λ2(3) 若t<s<t+1Cov(y(t),y(s))= E [x(t+1)-x(s)+x(s)-x(t)] [x(s+1)-x(t+1)+x(t+1)-x(s)]- λ2 =(x(t+1)-x(s))(x(s+1)-x(t+1))+E(x(t+1)-x(s))(x(t+1)-x(s))+E(x(s)-x(t))(x(s+1)-x(t+1))+E(x(s)-x(t))(x(t+1)-x(s))- λ2=0+λ(t+1-s)+0-λ2=λ+λ(t-s)- λ2(4) 若s>t+1 Cov(y(t),y(s))=0-λ2=-λ2由此知，故方差只与t-s有关，与t,s无关故此过程为宽平稳的。
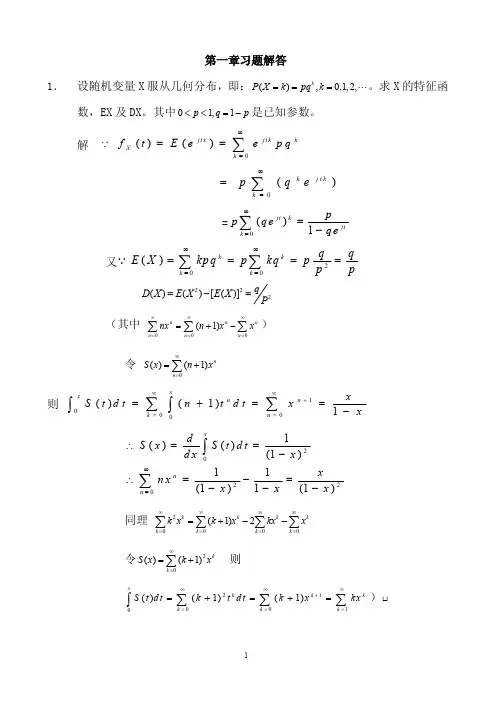
概率论与随机过程习题答案标准化工作室编码[XX968T-XX89628-XJ668-XT689N]《概率论与随机过程》第一章习题答案1. 写出下列随机试验的样本空间。
（1） 记录一个小班一次数学考试的平均分数（设以百分制记分）。
解： ⎭⎬⎫⎩⎨⎧⨯=n n nn S 100,,1,0 ，其中n 为小班人数。
（2） 同时掷三颗骰子，记录三颗骰子点数之和。
解：{}18,,4,3 =S 。
（3） 10只产品中有3只是次品，每次从其中取一只（取出后不放回），直到将3只次品都取出，记录抽取的次数。
解： {}10,,4,3 =S 。
（4） 生产产品直到得到10件正品，记录生产产品的总件数。
解： {} ,11,10=S 。
（5） 一个小组有A ，B ，C ，D ，E5个人，要选正副小组长各一人（一个人不能兼二个职务），观察选举的结果。
解： {}ED EC EB EA DE DC DB DA CE CD CB CA BE BD BC BA AE AD AC AB S ,,,,,,,,,,,,,,,,,,,=其中，AB 表示A 为正组长，B 为副组长，余类推。
（6） 甲乙二人下棋一局，观察棋赛的结果。
解： {}210,,e e e S =其中，0e 为和棋，1e 为甲胜，2e 为乙胜。
（7） 一口袋中有许多红色、白色、蓝色乒乓球，在其中任意取4只，观察它们具有哪几种颜色。
解： {}rwb wb rb rw b w r S ,,,,,,=其中，,,,b w r 分别表示红色、白色、蓝色。
（8） 对某工厂出厂的产品进行检查，合格的盖上“正品”，不合格的盖上“次品”，如连续查出二个次品就停止检查，或检查4个产品就停止检查，记录检查的结果。
解： {}1111,1110,1101,0111,1011,1010,1100,0110,0101,0100,100,00=S 其中，0为次品，1为正品。
（9） 有A ，B ，C 三只盒子，a ，b ，c 三只球，将三只球装入三只盒子中，使每只盒子装一只球，观察装球的情况。
随机过程习题解答第一章习题解答1．设随机变量X 服从几何分布，即：(),0,1,2,kP X k pqk ===。
求X 的特征函数，EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtk k X k f t E ee pq ∞===∑ =()1jt k jtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑（其中 0(1)nnnn n n nx n x x ∞∞∞====+-∑∑∑）令 0()(1)nn S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰同理 2(1)2kkkk k k k k kx k x kx x ∞∞∞∞=====+--∑∑∑∑令2()(1)kk S x k x ∞==+∑ 则211()(1)(1)xkk kk k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰）2、（1） 求参数为(,)p b 的Γ分布的特征函数，其概率密度函数为（2） 其期望和方差；（3）证明对具有相同的参数的b 的Γ分布，关于参数p 具有可加性。
解 （1）设X 服从(,)p b Γ分布，则 （2）'1()(0)Xp E X fjb∴==（4）若(,)i i X p b Γ 1,2i = 则同理可得：()()i i P X b f t b jt∑=∑-3、设ln (),()(kZ F X E Zk =并求是常数）。
X 是一随机变量，()F x 是其分布函数，且是严格单调的，求以下随机变量的特征函数。
（1）(),(0,)Y aF X b a b =+≠是常数； （2）ln (),()(kZ F X E Z k =并求是常数）。
解（1）11{()}{()}[()]P F x y P x F y F F y y --<=<==（01y ≤≤） ∴00()0111y F y yy y <⎧⎪=≤≤⎨⎪>⎩∴()F x 在区间[0，1]上服从均匀分布()F x ∴的特征函数为11001()(1)jtx jtx jt X e f t e dx e jt jt ===-⎰ （2）ln ()()()[]jtz jt F x Z f t E e E e ===1ln 01jt ye dy ⋅⎰=111jty dy jt =+⎰4、设12n X X X ，，相互独立，且有相同的几何分布，试求1nkk X =∑的分布。
