金属的功函数
- 格式:pdf
- 大小:286.76 KB
- 文档页数:6

常见金属材料功函数金属材料的功函数是指其中一种金属表面上需要供给的最小能量,以将一电子从金属表面抽离出来的过程。
它是金属物理性质的重要参数,与金属的导电性、光电效应、表面反应等密切相关。
以下将介绍常见金属材料的功函数。
1.铜(Cu)铜是常见的金属材料之一,其功函数约为4.7eV。
因为铜的功函数较高,所以它对光电效应的响应较弱,对光源要求较高。
铜具有良好的导电性和热传导性能,广泛应用于电子器件、电线电缆等领域。
2.铁(Fe)铁是一种重要的金属材料,其功函数约为4.5eV。
铁具有良好的导磁性和机械性能,广泛用于制造机械设备、建筑结构和电磁器件。
因为铁的功函数较高,所以它对光电效应的响应较弱,对于阳光的利用较不理想。
3.铝(Al)铝是一种轻金属,其功函数约为4.1eV。
铝具有良好的导电性和热导性,广泛用于制造飞机、汽车、建筑等领域。
铝的功函数较低,所以它对光电效应的响应较好,对太阳光的利用效率比较高。
4.锌(Zn)锌是一种常见的金属材料,其功函数约为4.3eV。
锌具有良好的抗腐蚀性和导电性能,广泛应用于锌电池、镀锌钢板等领域。
锌的功函数较低,所以它对光电效应的响应较好,对太阳光的利用效率较高。
5.银(Ag)银是一种重要的金属材料,其功函数约为4.3eV。
银具有良好的导电性和热导性能,广泛应用于电子器件、化学催化剂等领域。
银的功函数较低,所以它对光电效应的响应较好,适用于光电器件制造。
6.铂(Pt)铂是一种贵金属,其功函数约为5.7eV。
铂具有优异的化学稳定性和催化性能,广泛应用于化工、电子等领域。
铂的功函数较高,所以它对光电效应的响应较弱,对光源要求较高。
以上是常见金属材料的功函数介绍。
不同金属的功函数差异较大,这使得它们在电子器件、光电器件、化学反应等方面具有不同的应用潜力。
更深入地研究金属材料的功函数及其影响因素,有助于开发和优化金属材料的性能,满足不同领域的需求。

金属逸出功公式
金属逸出功公式是描述金属表面电子逸出的一种数学公式。
在金属表面,电子受到金属原子的束缚,需要克服金属原子的吸引力才能逸出金属表面。
金属逸出功公式描述了电子逸出所需要的能量与金属表面的物理性质之间的关系。
金属逸出功公式可以表示为:
Φ = hν - E
其中,Φ表示金属的逸出功,h表示普朗克常数,ν表示光子的频率,E表示金属表面的功函数。
这个公式说明了金属表面电子逸出所需要的能量与光子的频率和金属表面的物理性质之间的关系。
金属逸出功公式的应用非常广泛。
在光电子学中,金属逸出功公式被用来描述光电效应。
当光子照射到金属表面时,如果光子的能量大于金属的逸出功,那么金属表面的电子就会逸出。
这个过程被称为光电效应。
金属逸出功公式可以用来计算光电效应的能量阈值。
金属逸出功公式还被用来描述金属表面的化学反应。
在化学反应中,金属表面的电子可以参与反应,但是需要克服金属原子的吸引力才能离开金属表面。
金属逸出功公式可以用来计算化学反应中电子逸出所需要的能量。
金属逸出功公式是描述金属表面电子逸出的一种数学公式。
它可以
用来计算光电效应的能量阈值和化学反应中电子逸出所需要的能量。
这个公式的应用非常广泛,对于研究金属表面的物理和化学性质非常重要。


金属材料表面功函数的计算方法研究金属材料表面功函数是指单位面积表面上电子从表面跃迁至真空态需要克服的最小能量。
它是描述金属电子亲和力及气体分子吸附性质的重要物理量。
由于表面的微观结构和化学成分,不同金属材料的表面功函数差异较大,因此表面功函数的精确测量和计算十分重要。
一般来说,表面功函数可以通过实验方法和理论方法进行计算。
实验方法主要采用外场电子发射(外电场、光子能量等)和X射线光电子能谱(XPS)测量,其中XPS是目前最为常用的手段之一。
通过掌握基准样品的表面功函数值,可以计算出待测样品的表面功函数大小。
然而,这种方法的测量结果难以获得高精度,同时也受到基准样品和压力温度等外部因素的影响。
理论方法则主要采用量子化学计算方法,如密度泛函理论(DFT)、广义梯度近似(GGA)等。
其中DFT方法是目前最重要的一种理论计算方法,可以在原子层面上计算出基态电子密度及表面能,并得出表面功函数的值。
DFT方法可以通过建立复杂的晶格模型和考虑多种因素(如离子休克、晶格振动等)来提高计算精度和准确性,可以避免实验方法中受到外部因素影响的问题。
除DFT方法外,还存在一些其他理论计算方法,如累积梯度近似(LDA)、自洽电子结构计算方法(SCF)等。
这些方法在计算过程中通常需要考虑晶格对电子结构的影响,以及光子和电子间的相互作用等因素。
虽然这些方法的计算过程相对较为复杂,但是在某些情况下可以获得更优秀的计算结果。
目前,不同的计算方法在不同材料系统中的适用性正在不断探索和发展。
总而言之,金属材料表面功函数的精确计算对于材料科学和工程领域具有重要意义。
目前,实验方法和理论计算方法在对表面功函数进行研究上正不断完善,日益发展。
未来,表面功函数的测量和计算方法将进一步有望提高其计算精度和准确性,为材料表面技术开拓更广阔的应用前景。

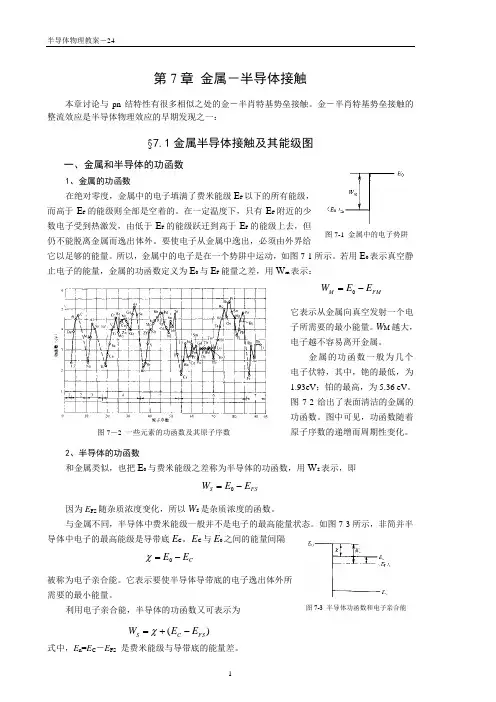
第7章 金属-半导体接触本章讨论与pn 结特性有很多相似之处的金-半肖特基势垒接触。
金-半肖特基势垒接触的整流效应是半导体物理效应的早期发现之一:§7.1金属半导体接触及其能级图一、金属和半导体的功函数1、金属的功函数在绝对零度,金属中的电子填满了费米能级E F 以下的所有能级,而高于E F 的能级则全部是空着的。
在一定温度下,只有E F 附近的少数电子受到热激发,由低于E F 的能级跃迁到高于E F 的能级上去,但仍不能脱离金属而逸出体外。
要使电子从金属中逸出,必须由外界给它以足够的能量。
所以,金属中的电子是在一个势阱中运动,如图7-1所示。
若用E 0表示真空静止电子的能量,金属的功函数定义为E 0与E F 能量之差,用W m 表示:FM M E E W -=0它表示从金属向真空发射一个电子所需要的最小能量。
W M 越大,电子越不容易离开金属。
金属的功函数一般为几个电子伏特,其中,铯的最低,为1.93eV ;铂的最高,为5.36 eV 。
图7-2给出了表面清洁的金属的功函数。
图中可见,功函数随着原子序数的递增而周期性变化。
2、半导体的功函数和金属类似,也把E 0与费米能级之差称为半导体的功函数,用W S 表示,即FS S E E W -=0因为E FS 随杂质浓度变化,所以W S 是杂质浓度的函数。
与金属不同,半导体中费米能级一般并不是电子的最高能量状态。
如图7-3所示,非简并半导体中电子的最高能级是导带底E C 。
E C 与E 0之间的能量间隔C E E -=0χ被称为电子亲合能。
它表示要使半导体导带底的电子逸出体外所需要的最小能量。
利用电子亲合能,半导体的功函数又可表示为)(FS C S E E W -+=χ式中,E n =E C -E FS 是费米能级与导带底的能量差。
图7-1 金属中的电子势阱图7-2 一些元素的功函数及其原子序数图7-3 半导体功函数和电子亲合能表7-1 几种半导体的电子亲和能及其不同掺杂浓度下的功函数计算值二、有功函数差的金属与半导体的接触把一块金属和一块半导体放在同一个真空环境之中,二者就具有共同的真空静止电子能级,二者的功函数差就是它们的费米能级之差,即W M -W S =E FS -E FM 。
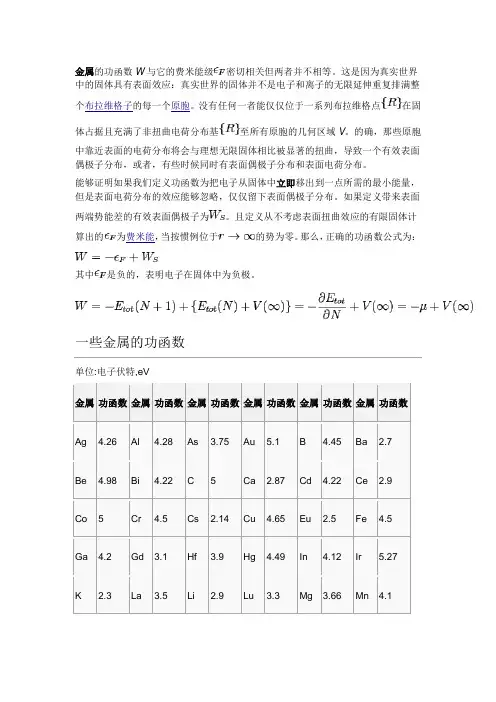
金属的功函数W与它的费米能级密切相关但两者并不相等。
这是因为真实世界中的固体具有表面效应:真实世界的固体并不是电子和离子的无限延伸重复排满整个布拉维格子的每一个原胞。
没有任何一者能仅仅位于一系列布拉维格点在固体占据且充满了非扭曲电荷分布基至所有原胞的几何区域V。
的确,那些原胞中靠近表面的电荷分布将会与理想无限固体相比被显著的扭曲,导致一个有效表面偶极子分布,或者,有些时候同时有表面偶极子分布和表面电荷分布。
能够证明如果我们定义功函数为把电子从固体中立即移出到一点所需的最小能量,但是表面电荷分布的效应能够忽略,仅仅留下表面偶极子分布。
如果定义带来表面两端势能差的有效表面偶极子为。
且定义从不考虑表面扭曲效应的有限固体计算出的为费米能,当按惯例位于的势为零。
那么,正确的功函数公式为:其中是负的,表明电子在固体中为负极。
单位:电子伏特,eV金属功函数金属功函数金属功函数金属功函数金属功函数金属功函数Ag 4.26 Al 4.28 As 3.75 Au 5.1 B 4.45 Ba 2.7Be 4.98 Bi 4.22 C 5 Ca 2.87 Cd 4.22 Ce 2.9Co 5 Cr 4.5 Cs 2.14 Cu 4.65 Eu 2.5 Fe 4.5Ga 4.2 Gd 3.1 Hf 3.9 Hg 4.49 In 4.12 Ir 5.27K 2.3 La 3.5 Li 2.9 Lu 3.3 Mg 3.66 Mn 4.1Simple Band Diagram with denoted vacuum energy EVAC, conduction band EC, Fermi energy EF, valence band EV, electron affinity Eea, work function Φ and band gap Eg1. 逸出电子是从哪来而来的?价带顶的电子2.能量是多少(Ec?还是EV?)?功函数=真空能级- 价带顶电子的能级3.功函数是一个统计值?从第二个问题的定义公式看,功函数不是一个统计值,而是一个确定值。
