【中小学资料】新沪科版初中数学七年级下册6.2第2课时实数的运算及大小比较教案.doc
- 格式:doc
- 大小:1.03 MB
- 文档页数:5



教案6.2实数第二课时安徽王玉杰教学目标:1、了解实数的意义,能对实数按要求进行分类。
2、了解实数范围内,相反数、倒数、绝对值的意义。
3、了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数。
重点、难点:重点:了解实数意义,能对实数进行分类,明确数轴上的点与实数一一对应并能用数轴上的点来表示无理数。
难点:用数轴上的点来表示无理数。
教学过程:一、创设问题情景,引出实数的概念1、什么叫无理数,什么叫有理数,举例说明。
2、把下列各数分别填入相应的集合内。
(1)你能把2,72,0.3,71-,4-,8,31,0,0.3737737773……(相邻两个3之间7的个数逐次增加1)等各数填入下面相应的集合中?正有理数:负有理数:有理数:无理数:(2)0属于正数吗?0属于负数吗?(3)实数除了可以分为有理数与无理数外,实数还可怎样分?让学生讨论回答后,教师引导学生形成共识:实数也可以分为正实数、0、负实数。
教师引导学生得出实数概述并板书:有理数和无理数统称实数(real number )。
教师点明:实数可分为有理数与无理数。
二、议一议1、了解实数范围内相反数、倒数、绝对值的意义:在有理数中,有理数a 的的相反数是什么,不为0的数a 的倒数是什么。
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
例如,2和2-是互为相反数,3和31互为倒数。
三、想一想让学生思考以下问题1、a 是一个实数,它的相反数为,绝对值为;2、如果,那么它的倒数为。
让学生回答后,教师归纳并板书:实数a 的相反数为a -,绝对值为a ,若 不为0,它的倒数为a 1(教师指明:0没有倒数四、实数运算1.例:计算①3233+②2132÷⨯分析:实数运算与有理数的运算一样,可以运用运算律。
解:按课本讲解。
2.实数大小比较类似有理数大小比较,实数大小比较3.一样地,在数轴上,右边的点比左边的点表示的数大。




实数的运算及大小比较-沪科版七年级数学下册教案一、知识点概述本节课讲解的是实数的运算及大小比较。
实数是数学中的一个基本概念,包括有理数和无理数两种类型。
实数的四则运算是数学中基本的运算之一,而实数的大小比较则是判断数的大小关系的重要方法。
在本节课中,学生需要掌握以下知识点:1.实数的概念和分类;2.实数的四则运算(加、减、乘、除);3.数的相反数和绝对值的概念和计算方法;4.计算带括号、带绝对值的实数运算;5.实数的大小比较。
二、教学目标1.理解实数的概念;2.掌握实数的分类方法;3.理解实数四则运算及其适用范围;4.掌握数的相反数和绝对值的概念和计算方法;5.掌握带括号、带绝对值的实数运算方法;6.掌握实数的大小比较方法。
三、教学重难点1.实数的四则运算;2.带括号、带绝对值的实数运算;3.实数的大小比较。
四、教学过程1. 课前导入通过让学生回答一些简单的问题,例如“你会区分有理数和无理数吗?”、“你知道实数的四则运算规则吗?”,来引导学生进入本节课的话题,激发学生的兴趣。
2. 新知讲解2.1 实数的概念和分类讲师首先向学生介绍实数的概念,包括有理数和无理数。
有理数是可以表示成两个整数的比值的数,无理数则不能,如根号2、圆周率等。
有理数和无理数统称为实数。
接下来,讲师让学生围绕数字轴上的点来演示实数的分类,以便深入理解实数。
学生应该理解实数包括正数、零、负数、有理数和无理数。
2.2 实数的四则运算讲师向学生清晰介绍实数的四则运算,包括加、减、乘、除。
在本节课的学习中,讲师重点强调实数同号之间进行加减法时的计算规则,以及不同号的实数相乘相除时的规则。
2.3 数的相反数和绝对值的概念和计算方法接下来,讲师解释了实数的相反数和绝对值的概念,并介绍了计算相反数和绝对值的规则。
2.4 计算带括号、带绝对值的实数运算讲师向学生解释了带括号、带绝对值的实数运算的计算方法,并以例子说明这些概念的应用。
在此过程中,讲师强调运算的顺序,以确保学生正确计算。
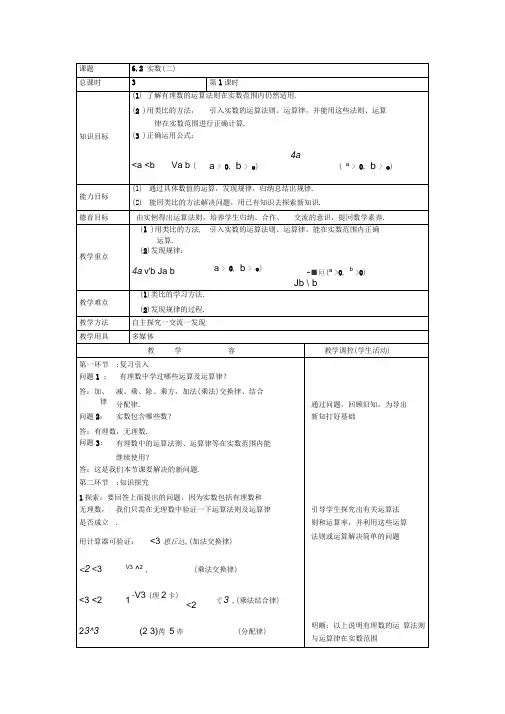

第2课时实数的运算及大小比较
1.了解实数与数轴的关系及实数范围内相反数、绝对值的意义;(重点)
2.理解有理数的运算法则和运算律在实数范围内仍适用,能进行实数的大小比较.(重点、难点)
一、情境导入
如图所示,小明家有一正方形厨房ABD和一正方形卧室EFG,其中正方形厨房ABD 的面积为10平方米,正方形卧室EFG的面积为15平方米,他想知道这两个正方形的边长之和BG的长是多少米,你能帮他计算出吗?
二、合作探究
探究点一:实数与数轴的关系
【类型一】求数轴上的点对应的实数
如图所示,数轴上A,B两点表示的数分别是-1和3,点B关于点A的对称点为,求点所表示的实数.
解析:首先结合数轴和已知条件可以求出线段AB的长度,然后利用对称的性质即
可求出点所表示的实数.
解:∵数轴上A,B两点表示的数分别为-1和3,∴点B到点A的距离为1+3则点到点A的距离也为1+3设点表示的实数为则点A到点的距离为-1-,∴-1-=1+3,∴=-2-3∴点所表示的实数为-2- 3
方法总结:本题主要考查了实数与数轴之间的对应关系,两点之间的距离为两数差的绝对值.
【类型二】利用数轴进行估算
如图所示,数轴上A,B两点表示的数分别是2和51,则A,B两点之间表示整数的点共有( )
A.6个B.5个.4个D.3个
解析:∵2≈1414,∴2和51之间的整数有2,3,4,5,∴A,B两点之间表示整数的点共有4个.故选
方法总结:要确定两点间的整数点的个数,也就是需要比较两个端点与邻近整点的大小,牢记数轴上右边的点表示的实数比左边的点表示的实数大.
【类型三】结合数轴进行化简
实数在数轴上的对应点如图所示,化简:a2-|b-a|-(b+c)2
解析:由于a2=|a|,(b+c)2=|b+c|,所以解题时应先确定a,b-a,b+c 的符号,再根据绝对值的意义化简.
解:由图可知a<0,b-a>0,b+c<0
所以,原式=|a|-|b-a|-|b+c|=-a-(b-a)+(b+c)=-a-b+a+b+c=c
方法总结:根据实数的绝对值的意义正确去绝对值符号是解题的关键:|a|=错误!
探究点二:实数的性质
求下列各数的相反数和绝对值:
(1)5;(2)2-3;(3)-1+ 3
解析:根据相反数、绝对值的定义求解.
解:(1)5的相反数是-5,绝对值是5;
(2)2-3的相反数是-2+3,绝对值是-2+3;
(3)-1+3的相反数是1-3,绝对值是-1+ 3
方法总结:只有符号不同的两个数互为相反数,求一个数的相反数时,只需在这个数的前面加上“-”号再去括号即可.求一个数的绝对值,需要分清这个数是正数、0还是负数.正数的绝对值是它本身,0的绝对值是0,负数的绝对值是它的相反数.探究点三:实数的运算
计算下列各式的值:
(1)23-55-(3-55);
(2)|3-2|+|1-2|+|2-3|
解析:按照实数的混合运算顺序进行计算.
解:(1)23-55-(3-55)
=23-55-3+5 5
=(23-3)+(55-55)
=3;
(2)因为3-2>0,1-2<0,2-3>0,
所以|3-2|+|1-2|+|2-3|
=(3-2)-(1-2)+(2-3)
=3-2-1+2+2- 3
=(3-3)+(2-2)+(2-1)=1
方法总结:进行实数的混合运算时,要注意运算顺序以及正确运用运算律.探究点四:实数的大小比较
比较大小:
(1)3-1
5
与
1
5
;(2)1-2与1- 3
解析:把两个数直接相减,根据差的正负比较大小.
解:(1)∵3-1
5
-
1
5
=
3-2
5
<0,∴
3-1
5
<
1
5
或
3-1
5
÷
1
5
=3-1<1,∴
3-1
5
<1
5
;
(2)∵(1-2)-(1-3)=3-2>0,∴1-2>1- 3
方法总结:作差法比较实数大小:设a,b为任意两个实数,先求出a与b的差,
再根据“当a-b<0时,a<b;当a-b=0时,a=b;当a-b>0时,a>b”比较a与b的大小.
三、板书设计
1.实数与数轴的关系
实数与数轴上的点一一对应.
2.实数的性质
有理数的相反数、倒数、绝对值的意义在实数范围内仍然有意义.
3.实数的运算
4.实数的大小比较
正数大于零,负数小于零,正数大于负数;两个正数,绝对值大的数较大;两个负数,绝对值大的数反而小.
由实际问题引入实数的运算,激发学生的学习兴趣.同时复习有理数的运算法则和运算律,并强调这些法则和运算律在实数范围内同样适用.教学中,让学生通过具体的运算(包含无理数的运算)感知运算法则和运算律,培养学生严谨务实、一丝不苟的学习态度。