比较以上各点的指标可知,b是最小指标点。但b不是目标
点,所以挖去b,于是可得: 精选ppt
14
(2)令T2=T1-{b}={c,d,e,f,g,z},T2中各点的指标为: DT2(c)=min(DT1(c), DT1(b)+W(b,c))=min(4,2+3)=4 (a c) DT2(d)= min(DT1(d), DT1(b)+W(b,d))=min(3,∞)=3 (a d)
最短路径问题
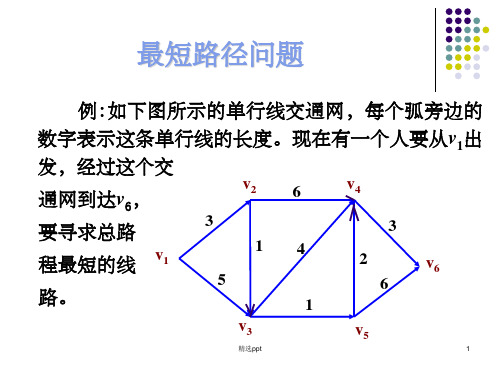
例:如下图所示的单行线交通网,每个弧旁边的
数字表示这条单行线的长度。现在有一个人要从v1出
发,经过这个交
通网到达v6, 要寻求总路 程最短的线 v1
路。
v2
6
3 14
5 1
v4
3
2
v6
6
v3
v5
精选ppt
1
从v1到v6的路线是很多的。比如从v1出发, 经过v2 ,v4到达v6或者从v1出发,经过v2,v3, v5到达v6等等。但不同的路线,经过的总长 度是不同的。例如,按照第一个线路,总长 度是3+6+3=12单位,按照第二个路线,总长 度是3+1+1+6=11单位。
精选ppt
2
一、问题的提法及应用背景
(1)问题的提法——寻求网络中两点间的最 短路就是寻求连接这两个点的边的总权数为 最小的通路。
(2)应用背景——管道铺设、交通网络、线 路安排、厂区布局、设备更新等。
精选ppt
3
二、赋权图的定义
在图的点或边上表明某种信息的数称为权。 含有权的图称为赋权图。 如图
c) b e) d f)
DT3(g)=min(DT2(g), DT2(d)+W(d,g))=min(∞,3+7)=10(a d g) DT3(z)=min(DT2(z), DT2(d)+W(d,z))=min(∞,∞)=∞