四年级仁华思维导引解析第1-20讲

小学四年级学习中的思维导应用技巧小学四年级学习中的思维导引应用技巧四年级是小学生学习的重要阶段，为了培养他们良好的学习习惯和提高他们的学习成绩，思维导引应用技巧是必不可少的。

本文将介绍一些适用于小学四年级学生的思维导引应用技巧，帮助他们更有效地学习。

一、问答法在学习过程中，采用问答法可以激发学生的思维，增强他们的记忆力和理解力。

当老师提问时，学生不仅要仔细聆听问题，还要思考并给出合理的回答。

在回答问题的同时，学生可以通过口头或书面的方式来表达，从而提高他们的表达能力。

值得注意的是，在提问时，老师应该注意问题的深入与启发性，让学生通过回答问题的过程来加深对知识的理解。

二、归纳法归纳法是一种从具体事物中总结出一般规律或结论的思维方法。

在学习中，学生可以通过观察和分析，将学过的知识进行归纳总结。

例如，在学习数学的时候，学生可以将不同类型的题目进行分类，并总结出解题的一般方法，这样既能加深对知识的理解，又能提高解题的能力。

三、类比法类比法是一种通过类比来理解和应用新知识的思维方式。

在学习中，学生可以将新知识与已经熟悉的知识进行类比，找出二者之间的共同点和相似之处。

这样可以帮助学生更好地理解新知识，从而提高学习效果。

例如，学习英语的时候，学生可以将英语单词与汉语词汇进行类比，找出它们在拼写和发音上的相似之处。

四、比较法比较法是一种通过比较来理解和分析事物之间的异同的思维方法。

在学习过程中，学生可以将相似的概念或事物进行比较，找出它们之间的共同点和区别，并通过思考和分析来加深对知识的理解。

例如，学习地理的时候，学生可以比较不同国家或地区之间的气候、地形等特点，从而更好地掌握地理知识。

五、联想法联想法是一种通过联想来理解和记忆事物的思维方法。

在学习中，学生可以将抽象的概念或知识与具体的形象或事物进行联想，从而更好地理解和记忆。

例如，在学习古诗词的时候，学生可以通过联想将生活中的场景与古诗中的意境相联系，这样可以更深刻地理解和记忆古诗的内容。

THSHtWWff. fSttfiae VHMll VM3mI«S^S> t*t»<l ☆ I.b & ：cttJiati*nii tmut. e* A ・ LU AR . S9KM*/»cM»an*•■鼻《••4・ C4k» --■ . euyAVM ■细r«»<i ☆I ■・"：•汁,AS«・GH ・《 n-tAftVMII. SBIKWItta■aswwtn”人«nai«・n2个o ••■■■SA[«々*■] ☆ ☆K ■・•】・ H3WMi*eT<XJW. UBS 初•・ WRM —tt*Pi It^tfwnMUt WnW- ■i ・MH ■汪 RH 吟費・"f FRi »ix ・i -ttArtfl. natTm. ■«£2r 正乃DST ・ AfleRii^tum. ■!我 £W»«4>O. IMdCWri. ・*・f ■ lllMl -iltftCTJB. 妞方*上敬十 14KI •兰叙•*, 卄代I It«*«»<• •£徘MM 巧2下■，QHt 柑E*••丽4*4x ・》«««/■■«，■ tfl»«£rftwr. MW ・r ・・4 ・2»eMR ・fiT ・.■«" £杠z 心IW 卜HI孔Kom ☆4.tfWMinffiAAO ®^0 ® △ FMM 小 N 4 4 ZHIRIH 心9l«»«l ☆ ☆弘・U・■ ■自■- S-ffiCfA-MIft ■»$><*- rt««e-^atw金一<MM*卜匸力dtmr- nelwr* ••VMIS* ■ ■ t* 2^ ETamAteft ft 2• 3■•n・i ifiUKKM. wm lyb ・・0^14- ■冲、■m&9S7・・ > B. X. HU只**«Mil «*<u a・ fi. 5?*we> mu^uxe^iiUK^*nu± >e*n*T^BUe<-S・・・GZA・B・t・a处*4輸1. 1 4. s. Mtft- WfltftIH-wHtnSl・Bs4 «*evhii«Bx?»»-w»««. fta»«n*ft±BmtCMVTkIX MM AfSii*tr< iaB4R2R< 十：.：WttAR, snium—i jtM—■丰*从A««*. «i>Tii- • A •只lUM%■•}«• H CS«PiSw->-4. ・gr—i7y Mmftan-..■•»，niM rawaaVKL "MlWKlvrim*、t«*<l ☆7- ab7nM4w«. *~f^*2muNnHr ■丄atc*M«*n.9i»«^vi nrcio. • d ®weuM-+iw». MTHj.4<tttMjivnt-ul4A*at ☆☆L EtiMx# "rXirSitayh 呎最■・机》・4 «IUT*«i£Q><l4^U«IHxtt-1xUtll -»a- <H1■T^HNEnV "VIlW2/V-«tHBWKUm *<¥74WIUT»4a ms 找射丄■衣粉WSm： .qiHHlkS依■*■(«-t«a£B -WMhM4^=iDWV4*Kn -Wir-WT® g：mr・>aix・c—丄岑•七・■«i^Mt*fM(MU74^l«9irr«SH 3te—”*fJMU?•卜•BHTVtfZ祢卑yRFUV+卯•fW>9*^：4ilA*・^BK+-V苹Tit■01 eiI””lH.glMKMW «M«a«n«■・ W < '佢lea丄•审*W4<ltf ・・fel44«*<H -MU -*«44avW：fW(T«tH«ai ■■ WWeVZH '•«•(!>■甘■■vilfi IK««IZQ A OI < I ♦ Is5*aW«M«W ■y. 'FW I W积WC fc.XF 击"Ffl. •♦|4A,・1 ☆☆n. «Et^«iB3tmimiE：m. XMtMta <.«.*. ii. M m£fr£r»«M«»«9b«卜DM.r1*1nafrbDr»・《■”卜EM7WW>"gpf，aRWl ■■“■wi”• I aiw.mfr-fl "P卄卄,■« + 3号nMUWBranMX ”"OmMOtMT^d亠亠〜2.・5・1儿》4・“+4・^・II. e»-»tM・nn・TT >>iuw0f ffioat-tiQwwuMti 2上匕kK・■WaAIMK・i ・W・ >i.AI(•■•■I fliTB. m«M4a金N*er ■益««•上annH'EWiWttincch i»mx0«M-上MiFbe «««*■• M■上■■C«*+S枷h(M-& ftV ■••MhMUetr卜ZA*九«*-o-(*<*<1 ☆☆☆M. 一•4**A 篌蓦vM—««I••匕■} snvm n>»・RffiR♦•丄fnaa lUVCliHac育W・-c-A-r-r*9-*-r- 4«K*7・, l*4*al ☆☆☆Ik «■< IB - £RMA>c・a❷.KC<0© BPtfACZHfcCe. - %iafi/dC'i«e.知liWw—Mimi■祈t ■ueas苔9t・»v，BZAMK as斤MMTWMM，HwmusffSMM，Ktwtl■上■ mwnww-fi dJM.AleiAwv] «ii«mu-ABi»eti*%u- KWUIHWK■二IIC>4U・ HBdMtUI FU・OKQBnW. MKItfOMIft. «X<A. mrinjvnixnfiinw. a 瓠■Pt・vr 抄恠■■mH. M—t«K.ft-f <4, z赛it・iaMflMc・rTgaDauBMu»r・ym”《> ea«.。

《仁华学校奥林匹克数学课本(小学四年级)》
上册
第1讲速算与巧算（三）
第2讲速算与巧算（四）
第3讲定义新运算
第4讲等差数列及其应用
第5讲倒推法的妙用
第6讲行程问题（一）
第7讲几何中的计数问题（一）
第8讲几何中的计数问题（二）
第9讲图形的剪拼（一）
第10讲图形的剪拼（二）
第11讲格点与面积
第12讲数阵图
第13讲填横式（一）
第14讲填横式（二）
第15讲数学竞赛试题选讲
下册
第1讲乘法原理
第2讲加法原理
第3讲排列
第4讲组合
第5讲排列组合
第6讲排列组合的综合应用
第7讲行程问题
第8讲数学游戏
第9讲有趣的数阵图（一）
第10讲有趣的数阵图（二）
第11讲简单的幻方及其他数阵图
第12讲数字综合题选讲
第13讲三角形的等积变形
第14讲简单的统筹规划问题第15讲数学竞赛试题选讲。

四年级数学思维训练导引(奥数)第15讲加法原理与乘法原理(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（四年级数学思维训练导引(奥数)第15讲加法原理与乘法原理(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为四年级数学思维训练导引(奥数)第15讲加法原理与乘法原理(word版可编辑修改)的全部内容。

第十五讲加法原理与乘法原理1．阿奇去吃午饭，发现附近的中餐厅有9个，西餐厅有3个，日式餐厅有2个．他准备找一家餐厅吃饭,一共有多少种不同的选择？2．阿奇进入一家中餐厅后，发现主食有3种，热菜有20种．他打算主食和热菜各买1种，一共有多少种不同的买法？3．老师要求冬冬在黑板上写出一个减法算式，而且被减数必须是两位数，减数必须是一位数，冬冬共有多少种不同的写法?4．传说地球上有7颗不同的龙珠,如果找齐这7颗龙珠，并且按照特定顺序排成一行就会有神龙出现．邪恶的沙鲁找到了这7颗龙珠，但是他不知道排列的特定顺序．请问：运气不好的沙鲁最坏要试几次才能遇见神龙？5．用红、黄、蓝三种颜色给图15-1的三个圆圈染色,一个圆圈只能染一种颜色,并且相连的两个圆圈不能同色，一共有多少种不同的染色方法？6．在图15-2中，从“北”字开始，每次向下移动到一个相邻的字可以读出“北京奥运会”，那么一共有多少种不同的读法?7．运动会中有四个跑步比赛项目，分别为50米、100米、200米、400米，规定每个参赛者只能参加其中的一项．甲、乙、丙、丁四名同学报名参加这四个项目，请问：(1）如果每名同学都可以任意报这四个项目，一共有多少种报名方法?（2)如果这四名同学所报的项目各不相同，一共有多少种报名方法？8．冬冬的书包里有5本不同的语文书、6本不同的数学书、3本不同的英语书,请问：（1）如果从中任取1本书，共有多少种不同的取法？(2)如果从中取出语文书、数学书、英语书各l本,共有多少种不同的取法？9．如图15-3，甲、乙两地之间有4条路，乙、丙两地之间有2条路，甲、丙两地之间有3条路，那么从甲地去丙地一共有多少条不同的路线？10.图15—4中有一个从A到曰的公路网络，一辆汽车从A行驶到曰，可以选择的最短路线一共有多少条？1．阿奇一家人外出旅游，可以乘火车，也可以乘汽车,还可以坐飞机，经过网上查询，出发的那一天中火车有4班，汽车有3班,飞机有2班，他们乘坐这些交通工具，一共可以有多少种不同的选择?2．“IMO”是“国际数学奥林匹克”的缩写,要求把这三个字母涂上三种不同的颜色，且每个字母只能涂一种颜色．现有五种不同颜色的笔,按上述要求能有多少种不同颜色搭配的“IMO”?3．书架上有三层书，第一层放了15本小说，第二层放了10本漫画，第三层放了5本科普书，并且这些书各不相同,请问：(1）如果从所有的书中任取1本，共有多少种不同的取法？（2)如果从每一层中各取1本，共有多少种不同的取法？（3）如果从中取出2本不同类别的书,共有多少种不同的取法？4．如图15-5，从甲地到乙地有3条路,从乙地到丙地有3条路，从甲地到丁地有2条路，从丁地到丙地有4条路．如果要求所走路线不能重复，那么从甲地到丙地共有多少条不同的路线?5．如图15-6,四张卡片上写有数字2、4、7、8．从中任取三张卡片，排成一行，就可以组成一个三位数．请问：一共可以组成多少个不同的三位数？其中有多少个不同的三位奇数?6．奥运场馆实行垃圾分类处理．每个地方放置五个垃圾桶，从左向右依次标明:电池、塑料、废纸、易拉罐、不可再造，如图15-7.现在准备把五个垃圾桶染成红、绿、蓝这3种颜色之一，要求相邻两个垃圾筒颜色不同，且回收废纸的垃圾桶不能染成红色，一共有多少种染色方法?7．如图15—8，把A、曰、C、D、E这五部分用4种不同的颜色染色，且相邻的部分不能使用同一种颜色，不相邻的部分可以使用同一种颜色,请问：这幅图共有多少种不同的染色方法?8．如图15—9，用红、蓝两种颜色来给图中的小圆圈染色,每个小圆圈只能染一种颜色．请问:(1)如果每个小圆圈可以随意染色，一共有多少种不同的染法？(2）如果要求关于中间那条竖线左右对称,一共有多少种不同的染法？9．甲、乙、丙、丁、戊五人要驾驶A、B、C、D、E这五辆不同型号的汽车．会驾驶汽车A的只有甲和乙，汽车E必须由甲、乙、丙三人中的某一人驾驶，则一共有多少种不同的安排方案？10。

第十五讲加法原理与乘法原理1．阿奇去吃午餐，发现邻近的中餐厅有9 个，西餐厅有 3 个，日式餐厅有 2个．他准备找一家餐厅吃饭，一共有多少种不一样的选择？2．阿奇进入一家中餐厅后，发现主食有 3 种，热菜有 20 种．他打算主食和热菜各买 1 种，一共有多少种不一样的买法？3．老师要求冬冬在黑板上写出一个减法算式，并且被减数一定是两位数，减数一定是一位数，冬冬共有多少种不一样的写法？4．传说地球上有7 颗不一样的龙珠，假如找齐这7 颗龙珠，并且依据特定顺序排成一行就会有神龙出现．险恶的沙鲁找到了这7 颗龙珠，可是他不知道摆列的特定次序．请问：运气不好的沙鲁最坏要试几次才能遇到神龙？5．用红、黄、蓝三种颜色给图15-1 的三个圆圈染色，一个圆圈只好染一种颜色，并且相连的两个圆圈不可以同色，一共有多少种不一样的染色方法？6．在图 15-2 中，从“北”字开始，每次向下挪动到一个相邻的字能够读出“北京奥运会”，那么一共有多少种不一样的读法？7．运动会中有四个跑步竞赛项目，分别为50 米、 100 米、 200 米、 400 米，规定每个参赛者只好参加此中的一项．甲、乙、丙、丁四名同学报名参加这四个项目，请问：(1)假如每名同学都能够任意报这四个项目，一共有多少种报名方法？(2)假如这四名同学所报的项目各不同样，一共有多少种报名方法？8．冬冬的书包里有 5 本不一样的语文书、 6 本不一样的数学书、 3 本不一样的英语书，请问：(1)假如从中任取 1 本书，共有多少种不一样的取法？(2)假如从中拿出语文书、数学书、英语书各 l 本，共有多少种不一样的取法？9．如图 15-3 ，甲、乙两地之间有 4 条路，乙、丙两地之间有2 条路，甲、丙两地之间有 3 条路，那么从甲地去丙地一共有多少条不一样的路线？10.图 15-4 中有一个从 A 到曰的公路网络，一辆汽车从 A 行驶到曰，能够选择的最短路线一共有多少条？1．阿奇一家人出门旅行，能够乘火车，也能够乘汽车，还能够坐飞机，经过网上查问，出发的那天中火车有4 班，汽车有 3 班，飞机有 2 班，他们乘坐这些交通工具，一共能够有多少种不一样的选择？2．“ IMO”是“国际数学奥林匹克”的缩写，要求把这三个字母涂上三种不同的颜色，且每个字母只好涂一种颜色．现有五种不一样颜色的笔，按上述要求能有多少种不一样颜色搭配的“IMO”？3．书架上有三层书，第一层放了15 本小说，第二层放了10 本漫画，第三层放了 5 本科普书，并且这些书各不同样，请问：(1)假如从全部的书中任取 1 本，共有多少种不一样的取法？(2)假如从每一层中各取 1 本，共有多少种不一样的取法？(3)假如从中拿出 2 本不一样类其他书，共有多少种不一样的取法？4．如图 15-5 ，从甲地到乙地有 3 条路，从乙地到丙地有 3 条路，从甲地到丁地有 2 条路，从丁地到丙地有 4 条路．假如要求所走路线不可以重复，那么从甲地到丙地共有多少条不一样的路线？5．如图 15-6 ，四张卡片上写有数字2、4、7、8．从中任取三张卡片，排成一行，就能够构成一个三位数．请问：一共能够构成多少个不一样的三位数？此中有多少个不一样的三位奇数？6．奥运场馆推行垃圾分类办理．每个地方搁置五个垃圾桶，从左向右挨次注明：电池、塑料、废纸、易拉罐、不行再造，如图15-7. 此刻准备把五个垃圾桶染成红、绿、蓝这 3 种颜色之一，要求相邻两个垃圾筒颜色不一样，且回收废纸的垃圾桶不可以染成红色，一共有多少种染色方法？7．如图 15-8 ，把 A、曰、C、D、E 这五部分用 4 种不一样的颜色染色，且相邻的部分不可以使用同一种颜色，不相邻的部分能够使用同一种颜色，请问：这幅图共有多少种不一样的染色方法？8．如图 15-9 ，用红、蓝两种颜色来给图中的小圆圈染色，每个小圆圈只好染一种颜色．请问：(1)假如每个小圆圈能够任意染色，一共有多少种不一样的染法？(2)假如要求对于中间那条竖线左右对称，一共有多少种不一样的染法？9．甲、乙、丙、丁、戊五人要驾驶 A 、B 、C 、D 、E 这五辆不一样型号的汽车． 会 驾驶汽车 A 的只有甲和乙，汽车E 一定由甲、乙、丙三人中的某一人驾驶，则一 共有多少种不一样的安排方案？10. 如图 15-10 ，4 枚同样的棋子放入 4x4 的方格内，每个方格只好放1 枚， 且要求每行每列最多只好放1 枚，一共有多少种不一样的放法？11. 图 15-11 是一个阶梯形方格表，在方格中放入5 枚同样的棋子，使得每行、每列中都只有1 枚棋子，这样的放法共有多少种？12．如图 15-12 和图 15-13 ，蚂蚁在线段上爬行， 只好依据箭头的方向行走， 请问：(1) 按图 15-12 所示，从 A 点走到 B 点的不一样路线有多少条？(2) 按图 15-13 所示，从 A 点走到 B 点的不一样路线有多少条？1．爸爸、妈妈带阿奇去吃西餐，餐厅里有米饭和面条 2 种主食，烤牛排、烤羊排和烤鸡排 3 种主菜，奶油蘑菇汤 1 种汤，以及蛋糕和布丁 2 种甜点，假如阿奇想重点 1 种主食和 1 种主菜，汤和甜点可点可不点，并且种类不限．请问：阿奇一共有多少种点菜方法？2．如图 15-14 ，在一个 3x4 的方格表内放人有 1 枚棋子，一共有多少种不一样的放法？假如放人列至多有 1 枚棋子，一共有多少种不一样的放法？4 枚同样的棋子， 要求每列至多 4 枚互不同样的棋子， 要求每3．如图 15-15 ，将图中的八个部分用红、 黄、绿、蓝这 4 种不一样的颜色染色，并且相邻的部分不可以使用同一种颜色， 不相邻的部分能够使用同一种颜色． 请问：这幅图共有多少种不一样的染色方法？4．用 4 种不一样的颜色给图 15-16 中的圆圈染色，有线段相连的两个圆圈不 能同色，一共有多少种不一样的染色方法？5．一只甲虫沿着图15-17 中的方格线从 A 爬到 B ，每次只好向右爬一格或向上爬一格．图中画着黑点的地方不可以经过． 请问：这只甲虫能够选择多少条不一样 的路线？6．王老师家装饰新房，需要 2 个木工和 2 个电工．现有木工 3 人、电工 3人，还有 1 人既能做木工也能做电工，要从这 7 人中精选出 4 人达成这项工作，共有多少种不一样的选法？7．如图 15-18 所示，一只小甲虫要从 A 点出发沿着线段爬到B 点，不可以重复经过任何点，试问：这只甲虫有多少种不一样的走法？8．如图 15-19 所示，国际象棋中的棋子“皇后”从左下角走到右上角，每步只好向右、向上或许向右上挪动任意多格，一共有多少种不一样的走法？。

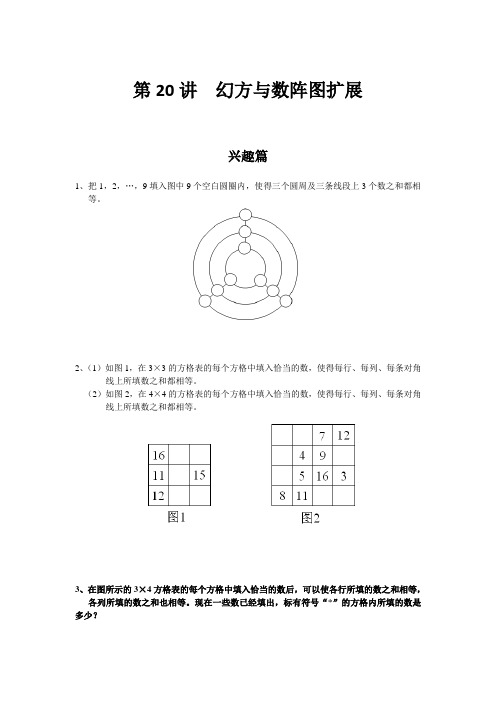
第20讲幻方与数阵图扩展兴趣篇1、把1，2，…，9填入图中9个空白圆圈内，使得三个圆周及三条线段上3个数之和都相等。

2、（1）如图1，在3×3的方格表的每个方格中填入恰当的数，使得每行、每列、每条对角线上所填数之和都相等。

（2）如图2，在4×4的方格表的每个方格中填入恰当的数，使得每行、每列、每条对角线上所填数之和都相等。

3、在图所示的3×4方格表的每个方格中填入恰当的数后，可以使各行所填的数之和相等，各列所填的数之和也相等。

现在一些数已经填出，标有符号“*”的方格内所填的数是多少？4、如图，请在空格中填入适当的数，组成一个三阶幻方。

5、请将图所示的5×5方格表补充完整，使得每个方格内都有一个数字，并且具有如下的性质：方格表中每行，每列和每条对角线的5个方格内所填的5个数中，1、2、3、4、5 恰好各出现一次。

请问：标有符号“△”，“▽”和“◯”的方格中所填的数分别是什么？6、请将1至9这9个数填入图中的方框内，使得所有不等号都成立。

所有满足要求的填法共有多少种？7、请在图所示的8个小圆圈内，分别填入1至8这8个数字，使得图中用线段连接的两个小圆圈内所填的数的差（大减小）恰好是1、2、3、4、5、6、7。

8、将1至5这5个数字填入图中的圆圈内，使得横线、竖线、大圆周上所填数之和都相等。

9、请在图中的六块区域内填入1、2、3、4、5、6，使得对每一个小圆圈来说，与它相邻的区域内的数之和都相等。

10、将0至9填入图的10块区域中（阴影区域除外），使得每个圆内的三个数之和都是相等的。

请问：这个和最小是多少？最大是多少？拓展篇1、将1，2，3，…，24，25分别填入图的各个方格中，使得每行、每列及两条对角线上的数的和相等。

现在已经填入了一些数，标有符号“*”的方格内所填的数是多少？2、请在图的每个空格内填入一个合适的数，使得每行、每列及两条对角线上的3个方格中的各数之和都相等。

华数导引四年级计数问题加法原理与乘法原理第08讲计数问题第02讲加法原理与乘法原理1、如果两个四位数的差等于8921，那么就说这两个四位数组成一个数对，问这样的数对共有多少个？分析：从两个极端来考虑这个问题：最大为9999-1078=8921，最小为9921-1000=8921，所以共有9999-9921+1=79个，或1078-1000+1=79个2、一本书从第1页开始编排页码，共用数字2355个，那么这本书共有多少页？分析：按数位分类：一位数：1～9共用数字1*9=9个；二位数：10～99共用数字2*90=180个；三位数：100～999共用数字3*900=2700个，所以所求页数不超过999页，三位数共有：2355-9-180=2166，2166÷3=722个，所以本书有722+99=821页。

3、上、下两册书的页码共有687个数字，且上册比下册多5页，问上册有多少页？分析：一位数有9个数位，二位数有180个数位，所以上、下均过三位数，利用和差问题解决：和为687，差为3*5=15，大数为：（687+15）÷2=351个（351- 189）÷3=54，54+99=153页。

4、从1、2、3、4、5、6、7、8、9、10这10个数中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积。

分析：从整体考虑分两组和不变：1+2+3+4+5+6+7+8+9+10=55 从极端考虑分成最小和最大的两组为（1+2+3+4+5）+（6+7+8+9+10）=15+40=55 最接近的两组为27+28 所以共有27-15+1=13个不同的积。

另从15到27的任意一数是可以组合的。

5、将所有自然数，自1开始依次写下去得到：12345678910111213……，试确定第206788个位置上出现的数字。

分析：与前面的题目相似，同一个知识点：一位数9个位置，二位数180个位置，三位数2700个位置，四位数36000个位置，还剩：206788-9-180-2700-36000=167899，167899÷5=33579……4 所以答案为33579+100=33679的第4个数字7.6、用1分、2分、5分的硬币凑成1元，共有多少种不同的凑法？分析：分类再相加：只有一种硬币的组合有3种方法；1分和2分的组合：其中2分的从1枚到49枚均可，有49种方法；1分和5分的组合：其中5分的从1枚到19枚均可，有19种方法；2分和5分的组合：其中5分的有2、4、6、……、18共9种方法；1、2、5分的组合：因为5=1+2*2，10=2*5，15=1+2*7，20=2*10，……，95=1+2*47，共有2+4+7+9+12+14+17+19+22+24+27+29+32+34+37+39+42+44+47=461种方法，共有3+49+19+9+461=541种方法。

四年级导引解析->《华数思维训练导引》四年级上学期还原与年龄华数思维训练导引----还原与年龄四年级上学期第03讲应用题第08讲1. 某数加上6，乘以6，减去6，除以6，其结果等于6，则这个数是多少？解答：（6×6+6）÷6-6=1，这个数是1.2. 两个两位数相加，其中一个加数是73，另一个加数不知道，只知道另一个加数的十位数字增加5，个位数字增加1，那么求得的和的后两位数字是72，问另一个加数原来是多少？解答：和的后两位数字是72，说明另一个加数是99。

十位数字增加5，个位数字增加1，那么原来的加数是99-51=48。

3. 有砖26块，兄弟二人争着去挑。

弟弟抢在前面，刚摆好砖，哥哥赶到了。

哥哥看弟弟挑的太多，就抢过一半。

弟弟不肯，又从哥哥那儿抢走一半。

哥哥不服，弟弟只好给哥哥5块，这时哥哥比弟弟多挑2块。

问最初弟弟准备挑多少块？解答：先看最后兄弟俩各挑几块：哥哥比弟弟多挑2块，这是一个和差问题，哥哥挑的块数=（26+2）÷2=14块，弟弟=26-14=12块；然后再还原：哥哥还给弟弟5块：哥哥=14-5=9块，弟弟=12+5=17块；弟弟把抢走的一半还给哥哥：哥哥=9+9=18块，弟弟=17-9=8块；哥哥把抢走的一半还给弟弟：弟弟原来是8+8=16块。

4. 甲、乙、丙三人钱数各不相同，甲最多，他拿出一些钱给乙和丙，使乙和丙的钱数都比原来增加了两倍，结果乙的钱最多；接着乙拿出一些钱给甲和丙，使甲和丙的钱数都比原来增加了两倍，结果丙的钱最多；最后丙拿出一些钱给甲和乙，使甲和乙的钱数都比原来增加了两倍，结果三人钱数一样多了。

如果他们三人共有81元，那么三人原来的钱分别是多少元？解答：三人最后一样多，那么每人都是81÷3=27元；还原：甲和乙把钱还给丙：每人增加2倍，就是原来的3倍，那么甲和乙都是27/3=9元，丙是27+2*2*9=63元；甲和丙把钱还给乙：甲=9/3=3元，丙=63/3=21元，乙=9+2*3+2*21=57元；乙和丙把钱还给甲：乙=57/3=19元，丙=21/3=7元，甲=3+2*19+2*7==55元。

第二十讲最优化问题第一部分：趣味数学数字、符号家族之怪事数字、符号两大家族素有严谨认真的好名声，但今天却来了几个不速之客，搅得沸沸扬扬。

这不!您瞧：“110年=几百万年”“=”手牵着这两个八杆子也打不着的数字，得意得直眨眼。

“>”，“<</span>”立即吵了起来：“明明是100年<</span>几百万年嘛！”“是呀！是呀！”“=”你站错了，该让“<</span>”才对！大家一起责怪起“=”来。

“=”笑着拉起一旁“<</span>”的手说：“你别急，你瞧我前面的提示就知道了！”哦！原来前面还闪着“人口爆炸”四个字。

大家还有些不解。

“我明白了，这是说世界人口增长速度很快，照这样下去，100年内增长的人口比几百万内增长的人口还多。

这位子让给你了！”原来如此！大家恍然大悟！话音未落，“>”身披彩带牵上了这么一组式子：4>5，咦！咄咄怪事。

“>”见大家一头雾水的样子，笑着说：“这是数学家聪聪的至理名言：掌握正确的学习方法，4小时学习的效率比5小时还大！”大家听了这话，拍起巴掌，直称好！接着其他符号“≠”“……”……都纷纷登台，演出一幕幕令人吃惊的好戏，引得前来观看的知识老爷爷连连摸着胡子说：“好！好！哈，哈……”通过本节趣味数学的教学使学生学会解决等式加减法类型的题目，渗透解方程的一些方法。

第二部分：奥数小练在日常生活和生产中，我们经常会遇到下面的问题：完成一件事情，怎样合理安排才能做到用的时间最少，效果最佳。

这类问题在数学中称为统筹问题。

我们还会遇到“费用最省”、“面积最大”、“损耗最小”等等问题，这些问题往往可以从极端情况去探讨它的最大（小）值，这类问题在数学中称为极值问题。

以上的问题实际上都是“最优化问题”。

【例题1】用一只平底锅煎饼，每次只能放两个，剪一个饼需要2分钟（规定正反面各需要1分钟）。

问煎3个饼至少需要多少分钟？【思路导航】先将两个饼同时放入锅中一起煎，一分钟后两个饼都熟了一面，这时可将一个取出，另一个翻过去，再放入第三个。

小学奥数书推荐(2011-04-11 15:23:24)转载▼分类：教育标签：教育/s/articlelist_1918334024_0_1.html西工大李老师小升初超常教育实验班：最强、最牛、最给力的小学奥数经典教材介绍1. 《仁华学校奥林匹克数学课本》(俗称“课本”，一共六册，从一年级到六年级)这套书写的非常详细，把小学奥数基本内容都涵盖了，而且内容不太复杂，非常适合让孩子自学！。

如果孩子不太自觉，那可以报一个班儿，让老师来教，监督孩子扎实地掌握里面的内容。

里头每一讲都既有例题又有练习，而且练习不光有答案，还有解答。

大家可以学完例题，然后做练习。

注意，练习一定要做，而且要一道不落！因为光看是绝对学不会数学的！三年级孩子比较适合从这套书入手开始奥数的学习。

需要注意的是这套书一二年级两本书编排的相对差一些，比如二年级很多计算学校课堂还没有学，但是题目中却经常出现（这对孩子理解会造成非常大的障碍）；二年级仁华课本中经常有枚举类问题（比如整数拆分问题等等），这类问题逻辑严谨性很高，对二年级学生来讲比较难，但是课本中很前面就出现了。

所以我们建议如果低年级学生学习该课本时，应该在相应章节讲之前补充适当的基础知识，一些较难的章节应适当放在后面学习。

另外，这套书成书较早，很多内容相对简单。

作为基础教材，必须有一个超前使用的意识。

比如三年级的孩子，不要仅仅局限于学习三年级的课本，很多四年级课本的知识也可以给孩子学，比如整数的简便运算，四年级课本里就有，但三年级的孩子完全可以学。

一般到了五年级，在接触了分数的四则运算之后，学习六年级课本里的绝大多数内容是没有问题的了，所以五年级的孩子就应该当六年级的孩子来看待了。

不过话说回来，超前学是一方面，无论如何学踏实是一定要有的，绝对不能盲目追求速度，学得囫囵吞枣。

2. 《仁华学校数学思维训练导引》（俗称“导引”，一共两册，三、四年级一册，五、六年级一册）这套书是其实就是习题集，而且是难题集。