北师大版高中数学选修2-1精选试题及答案

北师大版高二数学选修2-1试题及答案（选修2-1）孙 敏一、选择题（本大题共12小题，每小题6分，共72分） 1、a 3＞8是a ＞2的（ ）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分也非必要条件2、全称命题“所有被5整除的整数都是奇数”的否定是（ ） A ．所有被5整除的整数都不是奇数； B ．所有奇数都不能被5整除C ．存在一个被5整除的整数不是奇数；D ．存在一个奇数，不能被5整除3、抛物线281x y -=的准线方程是( )A ． 321=xB ． 2=yC ． 321=y D ． 2-=y4、有下列命题：①20ax bx c ++=是一元二次方程（0a ≠）；②空集是任何集合的真子集；③若a ∈R ，则20a ≥；④若,a b ∈R 且0ab >，则0a >且0b >．其中真命题的个数有（ ）A ．1B ． 2C ． 3D ． 45、椭圆1162522=+y x 的离心率为（ ） A ．35 B ． 34 C ．45 D ． 9256、以坐标轴为对称轴，以原点为顶点且过圆096222=++-+y x y x 的圆心的抛物线的方程是（ ）A ．23x y =或23x y -=B ．23x y =C ．x y 92-=或23x y =D ．23x y -=或x y 92=7、已知a ＝（2，－3，1），b ＝（4，－6，x ），若a ⊥b ，则x 等于（ ）A ．－26B ．－10C ．2D ．10 8、如图，空间四边形ABCD 中，M 、G 分别是BC 、CD 的中点，则BD BC AB 2121++等于（ ）A ．ADB ．GAC ．AGD ．MG9、已知A 、B 、C 三点不共线，对平面ABC 外的任一点O ，下列条件中能确定点M 与点A 、B 、C 一定共面的是（ ）A ．OM OA OB OC =++ B ． 2OM OA OB OC =--C ．1123OM OA OB OC =++D ．111333OM OA OB OC =++ 10、设3=a ，6=b ， 若a •b ＝9，则,<>a b 等于（ ）A ．90°B ．60°C ．120°D ．45°11、已知向量a ＝（1，1，－2），b ＝12,1,x ⎛⎫ ⎪⎝⎭，若a ·b ≥0，则实数x 的取值范围为（ ）A ．2(0,)3B ．2(0,]3 C ．(,0)-∞∪2[,)3+∞ D ．(,0]-∞∪2[,)3+∞ 12、设R x x ∈21,，常数0>a ，定义运算“﹡”：22122121)()(x x x x x x --+=*，若0≥x ，则动点),(a x x P *的轨迹是（ ）A ．圆B ．椭圆的一部分C ．双曲线的一部分D ．抛物线的一部分 二、填空题（本大题共5小题，每小题5分，共25分）20、（本小题满分11分）已知0≠ab ,求证1=+b a 的充要条件是02233=--++b a ab b a21、（本小题满分12分）如图，在正方体ABCD －A 1B 1C 1D 1中，E 、F 分别是BB 1、CD 的中点． （Ⅰ）证明：AD ⊥D 1F ； （Ⅱ）求AE 与D 1F 所成的角； （Ⅲ）证明：面AED ⊥面A 1FD 1．22、（本小题满分12分）设椭圆12222=b y a x ＋(a ＞b ＞0)的左焦点为F 1(－2，0)，左准线 L 1 ：ca x 2-=与x 轴交于点N （－3，0），过点N 且倾斜角为300的直线L 交椭圆于A 、B 两点。

北师大版高中数学选修2--1检测试题答案一、选择题（本大题共12小题，共60.0分） 1. 椭圆x 216+y 29=1中，以点M(1,2)为中点的弦所在直线斜率为( )A. 916B. 932C. 964D. −932【答案】D【解析】【分析】本题主要考查了椭圆的性质以及直线与椭圆的关系，考查直线的斜率，考查分析与计算能力，属于中档题．在解决弦的中点问题，常用“点差法”，设而不求，将弦所在直线的斜率、弦的中点坐标联系起来，相互转化，先设出弦的两端点的坐标，分别代入椭圆方程，两式相减后整理即可求得弦所在的直线的斜率． 【解答】解：设弦的两端点为A(x 1,y 1)，B(x 2,y 2)，代入椭圆得{x 1216+y 129=1x 2216+y 229=1, 两式相减得(x 1+x 2)(x 1−x 2)16+(y 1+y 2)(y 1−y 2)9=0，即(x 1+x 2)(x 1−x 2)16=−(y 1+y 2)(y 1−y 2)9，∴−9(x 1+x 2)16(y 1+y 2)=y 1−y2x 1−x2， 又M(1,2)为弦AB 的中点， ∴ x 1+x 2=2，y 1+y 2=4， ∴−9×216×4=y 1−y2x 1−x 2，即y 1−y 2x1−x 2=−932，∴弦所在的直线的斜率为−932，故选D ．2. 给出如下四个命题：①若“p 且q ”为假命题，则p 、q 均为假命题；②命题“若a >b ，则2a >2b −1”的否命题为“若a ≤b ，则2a ≤2b −1”；③“，x 2+1≥1”的否定是“，x 2+1<1”； ④在△ABC 中，“A >B ”是“sinA >sinB ”的充要条件． 其中正确的命题的个数是( ) A. 1 B. 2 C. 3 D. 4 【答案】C【解析】【分析】本题以命题的真假判断与应用为载体考查了复合命题，四种命题，全称命题，充要条件等知识点，属于中档题．根据复合命题真假判断的真值表，可判断①；根据四种命题的定义，可判断②；根据全称命题的否定，可判断③；根据充要条件的定义及三角形正弦定理，可判断④． 【解答】解：①若“p 且q ”为假命题，则p 、q 存在至少一个假命题，但不一定均为假命题，故错误；②命题“若a >b ，则2a >2b −1”的否命题为“若a ≤b ，则2a ≤2b −1”，故正确； ③“，x 2+1≥1”的否定是“，x 2+1<1”，故正确； ④在△ABC 中，A >B ⇔a >b ⇔2RsinA >2RsinB ⇔sinA >sinB ， 故“A >B ”是“sinA >sinB ”的充要条件，故正确． 故选C ．3. 一动圆P 过定点M(−4,0)，且与已知圆N ：(x −4)2+y 2=16相切，则动圆圆心P的轨迹方程是( )A. x 24−y 212=1(x ≥2) B. x 24−y 212=1(x ⩽2) C. x 24−y 212=1 D. y 24−x212=1 【答案】C【解析】【分析】本题考查圆与圆的位置关系，考查双曲线的定义，属于中档题．动圆圆心为P ，半径为r ，已知圆圆心为N ，半径为4，由题意知，动点P 到两定点的距离之差的绝对值为常数4，P 在以M 、N 为焦点的双曲线上，且2a =4，2c =8，从而可得动圆圆心P 的轨迹方程． 【解答】解：动圆圆心为P ，半径为r ，已知圆圆心为N ，半径为4， 由题意知：当动圆与圆N 外切时，|PM |=r ，|PN |=r +4， 所以|PN |−|PM |=4;当动圆与圆N 内切时，|PM |=r ，|PN |=r −4， 所以||PM |−|PN ||=4;即动点P 到两定点的距离之差的绝对值为常数4，故P 在以M 、N 为焦点的双曲线上，且2a =4，2c =8， ∴b =2√3．∴动圆圆心P 的轨迹方程为x 24−y 212=1．故选C ．4. 若点O 与点F 分别为椭圆x 24+y 23=1的中心和左焦点，点P 为椭圆上的任意一点，则OP ⃗⃗⃗⃗⃗ ⋅FP⃗⃗⃗⃗⃗ 的最大值为( ) A. 2 B. 3 C. 6 D. 8 【答案】C【解析】【分析】本题考查椭圆的方程、几何性质、平面向量的数量积的坐标运算、二次函数的单调性与最值，考查了综合应用能力、运算能力，属于中档题．先求出左焦点坐标F ，设P(x 0,y 0)，根据P(x 0,y 0)在椭圆上可得到x 0、y 0的关系式，表示出向量FP ⃗⃗⃗⃗⃗ 、OP ⃗⃗⃗⃗⃗ ，根据数量积的运算将x 0、y 0的关系式代入组成二次函数进而可确定答案． 【解答】解：由题意，F(−1,0)，设点P(x 0,y 0)，则有x 024+y 023=1，解得y 02=3(1−x 024)，因为FP ⃗⃗⃗⃗⃗ =(x 0+1,y 0)，OP ⃗⃗⃗⃗⃗ =(x 0,y 0)，所以OP ⃗⃗⃗⃗⃗ ⋅FP ⃗⃗⃗⃗⃗ =x 0(x 0+1)+y 02 =x 024+x 0+3=14(x 0+2)2+2，此二次函数对应的抛物线的对称轴为x 0=−2，因为−2≤x 0≤2，所以当x 0=2时，OP⃗⃗⃗⃗⃗ ⋅FP ⃗⃗⃗⃗⃗ 取得最大值224+2+3=6， 故选：C ．5. 下列命题中真命题的个数是( )①∀x ∈R ，x 4>x 2；②若“p ∧q ”是假命题，则p ，q 都是假命题；③命题“∀x ∈R ，x 3−x 2+1≤0”的否定是“∃x ∈R ，x 3−x 2+1>0”． A. 0 B. 1 C. 2 D. 3 【答案】B【解析】【分析】此题是个基础题．考查命题的否定和复合命题的真假判定方法等基础知识，考查学生对基础知识的记忆和理解．要说明一个命题不正确，举出反例即可①当x =0时不等式不成立，②根据复合命题真值表可知，“p ∧q ”是假命题，只需两个命题中至少有一个为假即可；③全称命题的否定是特称命题，既要对全称量词进行否定，又要否定结论，故正确． 【解答】 解：易知①当x =0时不等式不成立，对于全称命题只要有一个情况不满足，命题即假； ②错，只需两个命题中至少有一个为假即可； ③正确，全称命题的否定是特称命题， 即只有一个命题是正确的， 故选B ．6. 已知椭圆x 24+y 2b2=1(0<b <2)的左右焦点分别为F 1，F 2，过F 1的直线l 交椭圆于A ，B 两点，若|BF 2|+|AF 2|的最大值为5，则b 的值是( )A. √3B. √2C. 32D. 1【答案】A【解析】【分析】本题主要考查椭圆的定义的应用，属中档题.三角形AF 2B 为焦点三角形，根据椭圆方程，即可求出三角形AF 2B 的周长，欲使|BF 2|+|AF 2|的最大，只须|AB|最小，利用椭圆的性质即可得出答案。

选修2－1姓名：张平安一 选择题（本题共12个小题，每小题只有一个正确答案，每小题5分，共60分）1．x>2是24x >的 （ ）A. 充分不必要条件B. 必要不充分条件C. 既充分又必要条件D. 既不充分又不必要条件2．命题“在ABC 中，若21sin =A ，则A=30º”的否命题是 （ ）A.在ABC 中，若21sin =A ，则A≠30ºB. 在ABC 中，若1sin 2A ≠，则A=30ºC.在ABC 中，若1sin 2A ≠，则A≠30ºD .以上均不正确3．已知命题P ：若a b ≥，则c>d ，命题Q ：若e f ≤，则a b <。

若P 为真且Q的否命题为真，则“c d ≤”是“e f ≤的”（ ）A ．充分条件B ．必要条件C ．充要条件D ．既不充分也不必要条件4、在平行六面体ABCD-A 1B 1C 1D 1中，M 为AC 与BD 的交点，若11A B a =,b D A =11，c A A =1，则下列向量中与M B 1相等的向量是A 、c b a ++-2121B 、c b a ++2121 C 、 c b a +-2121 D 、 c b a +--2121 5、空间直角坐标系中，O 为坐标原点，已知两点A （3，1，0），B （-1，3，0），若点C 满足OC =αOA +βOB ，其中α，β∈R ，α+β=1，则点C 的轨迹为 A 、平面 B 、直线 C 、圆D 、线段6、已知a =(1,2,3),b =（3，0，-1），c =⎪⎭⎫⎝⎛--53,1,51给出下列等式：①∣c b a ++∣=∣c b a --∣ ②c b a ⋅+)( =)(c b a +⋅ ③2)(c b a ++=222c b a ++④c b a ⋅⋅)( =)(c b a ⋅⋅其中正确的个数是 A 、1个 B 、2个 C 、3个 D 、4个7.已知椭圆125222=+y ax )5(>a 的两个焦点为1F 、2F ，且8||21=F F ，弦AB过点1F ，则△2ABF 的周长为（ ） （A ）10 （B ）20 （C ）241（D ） 4148.椭圆13610022=+y x 上的点P 到它的左准线的距离是10，那么点P 到它的右焦点的距离是（ ）（A ）15 （B ）12 （C ）10 （D ）89.椭圆192522=+y x 的焦点1F 、2F ，P 为椭圆上的一点，已知21PF PF ⊥，则△21PF F 的面积为（ ）（A ）9 （B ）12 （C ）10 （D ）810.椭圆141622=+y x 上的点到直线022=-+y x 的最大距离是（ ）（A ）3（B ）11（C ）22（D ）1011.过抛物线2y ax =(a>0)的焦点F 作一直线交抛物线于P 、Q 两点，若线段PF 与FQ 的长分别为p 、q ，则11p q+等于（ ）（A ）2a （B ）12a （C ）4a （D ）4a12. 如果椭圆193622=+yx 的弦被点(4，2)平分，则这条弦所在的直线方程是（ ）（A ）02=-y x （B ）042=-+y x （C ）01232=-+y x （D ）082=-+y x 二．填空题（本大题共4个小题，每小题4分，共16分） 13、“末位数字是0或5的整数能被5整除”的 否定形式是 否命题是14.与椭圆22143x y +=具有相同的离心率且过点（2，3方程 。

AA 1 DCB B 1C 1 图高二数学（选修2-1）空间向量试题一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共60分）． 1．在正三棱柱ABC —A 1B 1C 1中，若AB ＝2BB 1，则AB 1与C 1B 所成的角的大小为（ ）A ．60°B ．90°C ．105°D ．75°2．如图，ABCD—A 1B1C1D 1是正方体，B 1E 1＝D 1F 1＝411B A ，则BE 1与DF 1所成角的余弦值是（ ）A ．1715 B ．21 C ．178 D ．23 3．如图，A 1B 1C 1—ABC 是直三棱柱，∠BCA =90°，点D 1、F 1分别是A 1B 1、A 1C 1的中点，若BC =CA =CC 1，则BD 1与AF 1所成角的余弦值是（ ）A ．1030B ．21C ．1530D ．10154．正四棱锥S ABCD -的高2SO =，底边长AB =，则异面直线BD 和SC 之间的距离（ ）A ．515 B ．55 C ．552 D ．1055．已知111ABC A B C -是各条棱长均等于a 的正三棱柱，D 是侧棱1CC 的中点．点1C 到平面1AB D 的距离（ ）A ．a 42 B ．a 82 C ．a 423 D ．a 226．在棱长为1的正方体1111ABCD A B C D -中，则平面1AB C 与平面11A C D 间的距离（ ）A ．63 B ．33 C ．332 D ．23 7．在三棱锥P －ABC 中，AB ⊥BC ，AB ＝BC ＝21PA ，点O 、D 分别是AC 、PC 的中点，OP ⊥底面ABC ，则直线OD 与平面PBC 所成角的正弦值（ ）A ．621 B ．338 C60210 D ．302108．在直三棱柱111C B A ABC -中，底面是等腰直角三角形，90=∠ACB ，侧棱21=AA ，D ，E 分别是1CC 与B A 1的中点，点E 在平面AB D 上的射影是ABD ∆的重心G ．则B A 1与平面AB D 所成角的余弦值（ ）A ．32B ．37C ．23 D ．73 9．正三棱柱111C B A ABC -的底面边长为3，侧棱3231=AA ，D 是C B 延长线上一点，且BC BD =，则二面角B AD B --1的大小（ ）A ．3π B ．6π C ．65πD ．32π10．正四棱柱1111D C B A ABCD -中，底面边长为22，侧棱长为4，E ，F 分别为棱AB ，CD 的中点，G BD EF =⋂．则三棱锥11EFD B -的体积V （ ）A ．66B ．3316 C ．316D ．1611．有以下命题：①如果向量b a ,与任何向量不能构成空间向量的一组基底，那么b a ,的关系是不共线； ②,,,O A B C 为空间四点，且向量OC OB OA ,,不构成空间的一个基底，则点,,,O A B C一定共面；③已知向量,,是空间的一个基底，则向量,,-+也是空间的一个基底。

陕西省金台高级中学2018——2018学年度理科数学试题（选修2-1）一.选择题：（32分）1.已知),0,1,1(),3,3,0(-==，则向量与的夹角为（ ） A.030 B.045 C.060 D.0902.1<x<2是 x>0的（ ）条件A.必要不充分B.充要C.充分不必要D.既不充分也不必要3.若焦点在x 轴上的椭圆1222=+my x 的离心率为21，则m=（ ）A.3B.23 C.38 D.324. 以x=－41为准线的抛物线的标准方程为 （ ） A.y 2=21x B.y 2=x C.x 2=21y D.x 2=y5.设F 1和F 2为双曲线-42x y 2＝1两个焦点，点P 在双曲线上，满足∠F 1PF 2＝90°，则△F 1PF 2的面积是（ ） A ．1 B ．25C ．2D ．5 6.△ABC 中，D 为AB 边上一点，若1AD=2DB,CD=CA+λCB 3，则λ的值为（ ）A.32 B.31 C.31- D.32- 7.若椭圆154116252222=-=+y x y x 和双曲线的共同焦点为F 1，F 2，P 是两曲线的一个交点，则|PF 1|·|PF 2|的值为（ ） A.221B.84C.3D.21 8.已知命题p ：实数m 满足01≤-m ，命题q ：函数xm y )49(-=是增函数。

若q p ∨为真命题，q p ∧为假命题，则实数m 的取值范围为（ ） A.（1，2） B.（0，1） C. [1，2] D. [0，1] 二.填空题：（24分）9.命题“01,200<+∈∃x R x ”的否定是____________10.向量),,,2(),2,2,1(y x -=-=且→→b a //则x-y= 11.抛物线的的方程为22x y =，则抛物线的焦点坐标为____________ 12.设向量=++===>=>=<<⊥→→→→→→→→→→→→c b a c b a c b c a b a 则，且,3,21,3,,,π13.不等式kx 2+kx+1>0恒成立的充要条件是14.椭圆)0(12222>>=+b a by a x 的两个焦点是F 1、F 2，以| F 1F 2 |为边作正三角形，若椭圆恰好平分三角形的另两边，则椭圆的离心率为__________三.解答题（8分+10分+10分+8分+8分=44分）15.已知双曲线的中心在原点，焦点为FF 2（0，且离心率e =16.如图，在长方体AC 1中，AB=BC=2，AA 1=2，E.F 分别是面A 1C 1.面BC 1的中心，求（1）AF 和BE 所成的角.（2）AA 1与平面BEC 1所成角的正弦值.17.已知p:实数x满足22430x ax a -+<，其中a<0;q:实数x满足2260280x x x x --≤+->或且p q ⌝⌝是的必要不充分条件，求a 的范围.18.抛物线的焦点在x 轴上，经过焦点且倾斜角为135︒的直线，被抛物线所截得的弦长为8，试求抛物线的标准方程.19. 已知椭圆的一个顶点为A （0，-1），焦点在x 轴上.若右焦点到直线022=+-y x 的距离为3.(1)求椭圆的方程;(2)设椭圆与直线)0(≠+=k m kx y 相交于不同的两点M ，N.当AN AM =时，求m 的取值范围.AA 1BCDB 1C 1D 1EF参考答案一、选择题二、填空题 9. 2,10x R x ∀∈+≥ 10. -8 11. （18，0）12. 13. 04k <<14. 1三、解答题15.221,44y x y x -==±16. （1）90 （217. ]2(,4,03⎡⎫-∞-⋃-⎪⎢⎣⎭18.24y x =±19. （1）2213x y += （2）1(,2)2m ∈。

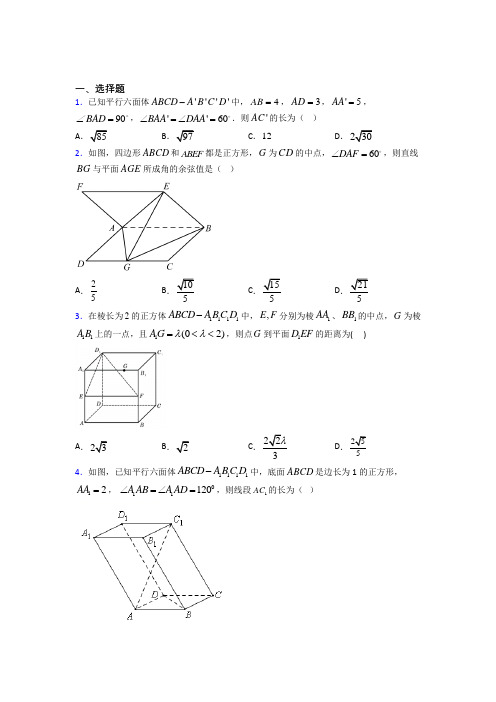
一、选择题1．已知平行六面体''''ABCD A B C D -中，4AB =，3AD =，'5AA =，90BAD ∠=，''60BAA DAA ∠=∠=．则'AC 的长为（ ）A ．85B ．97C ．12D ．230 2．如图，四边形ABCD 和ABEF 都是正方形，G 为CD 的中点，60DAF ∠=，则直线BG 与平面AGE 所成角的余弦值是（ ）A ．25B ．105C ．155D ．2153．在棱长为2的正方体1111ABCD A BC D -中，,E F 分别为棱1AA 、1BB 的中点，G 为棱11A B 上的一点，且1(02)AG λλ=<<，则点G 到平面1D EF 的距离为( )A ．23B ．2C ．223λD ．2554．如图，已知平行六面体1111ABCD A BC D -中，底面ABCD 是边长为1的正方形，12AA =， 011120A AB A AD ∠=∠=，则线段1AC 的长为（ ）A ．2B ．1C ．2D ．35．已知正方体1111ABCD A BC D -,M 为11A B 的中点，则异面直线A M 与1BC 所成角的余弦值为（ ）A ．105B ．1010C ．32D ．626．如图是由16个边长为1的菱形构成的图形，菱形中的锐角为,3π=,,a AB b CD =则=a b ⋅A ．5-B ．1-C ．3-D ．6-7．在空间直角坐标系Oxyz 中,已知(2,0,0)(2,2,0),(0,2,0),(1,1,2)A B C D .若123,,S S S 分别是三棱锥D ABC -在坐标平面上的正投影图形的面积，则（ ） A ．123S S S ==B ．21=S S 且23S S ≠C ．31S S =且32S S ≠D ．32S S =且31S S ≠8．圆锥的轴截面SAB 是边长为2的等边三角形，O 为底面的中心，M 为SO 的中点，动点P 在圆锥底面内（包括圆周）若,AM MP ⊥则点P 形成的轨迹的长度为( ) A ．76 B ．75 C ．72 D ．749．如图，在棱长为2的正方体1111ABCD A BC D -中，点E F 、分别是棱AB 、BC 的中点，则点1C 到平面1B EF 的距离等于（ ）A ．23B ．223C ．33D ．4310．如图，四棱锥P ABCD -的底面是边长为2的正方形， Q 为BC 的中点，PQ ⊥面ABCD ，且2PQ =，动点N 在以D 为球心半径为1的球面上运动，点M 在面 ABCD内运动，且PM 5=，则MN 长度的最小值为（ ）A ．352-B ．23-C ．25-+D ．332- 11．如图，棱长为1的正方体1111ABCD A BC D -，O 是底面1111D C B A 的中心，则O 到平面11ABC D 的距离是（ ）A ．12B ．24C ．22D 312．在平面直角坐标系中，()2,3A -、()32B -，，沿x 轴将坐标平面折成60︒的二面角，则AB 的长为（ ）A 2B ．211C ．32D ．42二、填空题13．在空间四边形ABCD 中，连接AC 、BD ,若BCD 是正三角形，且E 为其中心，则1322AB BC DE AD +--的化简结果为________． 14．已知三棱柱ABC ﹣A 1B 1C 1中，AA 1⊥面ABC ，AB ⊥AC ，且AA 1=AB=AC ，则异面直线AB 1与BC 1所成角为_____．15．已知平面向量()21,3m =+a 与()2,m =b 是共线向量且0⋅<a b ,则=b __. 16．已知四边形ABCD 为平行四边形，且A (4,1,3)，B (2，－5,1)，C (3,7，－5)，则顶点D 的坐标为________．17．如图所示，在正四棱柱1111ABCD A BC D -中，12AA =，1AB BC ==，动点P 、Q 分别在线段1C D 、AC 上，则线段PQ 长度的最小值是______．18．如图，空间四边形OABC 中，,M N 分别是对边,OA BC 的中点，点G 在线段MN 上，分MN 所成的定比为2，OG xOA yOB zOC =++，则,,x y z 的值分别为_____．19．在空间直角坐标系O xyz -中，点(1,2,3)A -到原点的距离为__________．20．三棱锥V-ABC 的底面ABC 与侧面VAB 都是边长为a 的正三角形，则棱VC 的长度的取值范围是_________.三、解答题21．在①()()DE CF DE CF +⊥-，②17||2DE =，③0cos ,1EF DB <<这三个条件中任选一个，补充在下面的横线中，并完成问题.问题：如图，在正方体1111ABCD A BC D -中，以D 为坐标原点，建立空间直角坐标系D xyz -.已知点1D 的坐标为()0,0,2，E 为棱11D C 上的动点，F 为棱11B C 上的动点，___________，试问是否存在点E ，F 满足1EF AC ⊥？若存在，求AE BF ⋅的值；若不存在，请说明理由.注：如果选择多个条件分别解答，按第一个解答计分.22．如图.四棱柱ABCD-A 1B 1C 1D 1的底面是直角梯形，BC ∥AD ，AB AD ，AD=2BC=2，四边形ABB 1A 1和ADD 1A 1均为正方形.（1）证明；平面ABB 1A 1平面ABCD ；（2）求二面角B 1 CD-A 的余弦值.23．如图，在四棱锥S ABCD -中，SA ⊥平面ABCD ，//AD BC ，AD AB ⊥，4AB AS ==，3AD =，6BC =，E 为SB 的中点．（1）求证：//AE 平面SCD ．（2）求二面角B AE C --的余弦值．24．如图，四棱锥P ABCD -的底面ABCD 是边长为2的菱形，60BAD ∠=，已知2,6PB PD PA ===，E 为PA 的中点．（1）求证PC BD ⊥；（2）求直线PC 与平面 PBD 所成角的正弦值．（3）求二面角B PC E --的余弦值．25．如图，平面ABCD ⊥平面ABEF ，其中四边形ABCD 为正方形，四边形ABEF 为直角梯形，1//902AB AF BE AF BE BAF ==∠=︒，，，M 为线段CE 上一点，//MF 平面ABCD ．（1）确定点M 的位置，并证明你的结论；（2）求直线DF 与平面BFM 所成角的正弦值．26．如图，四棱锥中P ABCD -中，底面ABCD 是直角梯形，//AB CD ，60DAB ∠=︒，2AB AD CD ==，侧面PAD ⊥底面ABCD ，且PAD △为等腰直角三角形，90APD ∠=︒．（Ⅰ）求证：AD PB ⊥；（Ⅱ）求平面PAD 与平面PBC 所成锐二面角的余弦值．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】用空间向量基本定理表示出AC '，然后平方后转化为数量积的运算求得．【详解】记a AB =，b AD =，c AA '=，则43cos900a b ⋅=⨯⨯︒=，同理152b c ⋅=，10a c ⋅=，由空间向量加法法则得AC a b c '=++， ∴22222()222AC a b c a b c a b b c a c '=++=+++⋅+⋅+⋅222154352210852=+++⨯+⨯=， ∴85AC '=AC '=．故选：A ．【点睛】方法点睛：本题考查求空间线段长，解题方法是空间向量法，即选取基底，用基底表示出向量，然后利用向量模的平方等于向量的平方转化为向量的数量积进行计算．2．C解析：C【分析】 以A 为原点，以AD 、AB 的方向分别为x 、y 轴的正方向，过A 作垂直平面ABCD 的直线作z 轴建立空间直角坐标系，设2AB =，利用空间向量法可求得直线BG 与平面AGE 所成角的正弦值，再利用同角三角函数的基本关系可求得结果.【详解】以A 为原点，以AD 、AB 的方向分别为x 、y 轴的正方向，过A 作垂直平面ABCD 的直线作z 轴，建立如图所示的空间直角坐标系A xyz -．设2AB =，得()0,0,0A 、()2,1,0G 、()0,2,0B 、(1,3E ，则()2,1,0AG =，(3AE =，()2,1,0BG =-，设平面AGE 的法向量为(),,n x y z =， 则20230n AG x y n AE x y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取1x =，则2y =-，3z = 所以，平面AGE 的一个法向量为(1,2,3n =-， 从而10cos ,225n BGn BG n BG ⋅<>===⨯⋅， 故直线BG 与平面AGE 2101515⎛⎫-= ⎪ ⎪⎝⎭. 故选：C.【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin h lθ=（l 为斜线段长），进而可求得线面角； （3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.3．D解析：D【分析】以D 为原点，DA 为x 轴、DC 为y 轴、1DD 为z 轴，建立空间直角坐标系，利用向量法能求出点G 到平面1D EF 的距离 .【详解】以D 为原点，DA 为x 轴、DC 为y 轴、1DD 为z 轴，建立空间直角坐标系， 则()()()()12,,2,0,0,2,2,0,1,2,2,1G D E F λ，()()()12,0,1,0,2,0,0,,1ED EF EG λ=-==，设平面1D EF 的法向量(),,n x y z =，则12020n ED x z n EF y ⎧⋅=-+=⎨⋅==⎩，取1x =，得()1,0,2n =，∴点G 到平面1D EF 的距离为 2255EG nd n ⋅===，故选D. 【点睛】本题主要考查利用空间向量求点到平面的距离，是中档题. 空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离. 4．A解析：A【分析】由11AC AB BC CC =++，两边平方，利用数量积的运算法则及数量积公式能求出21AC 的值，从而可得结果.【详解】平行六面体1111ABCD A BC D -中，底面ABCD 是边长为1的正方形，1112,120AA A AB A AD =∠=∠=， 11AC AB BC CC ∴=++，()2211AC AB BC CC ∴=++222111222AB BC CC AB CC BC CC AB BC =+++⋅+⋅+⋅ 114212cos120212cos12002=+++⨯⨯⨯+⨯⨯⨯+=， ∴线段1AC 的长为12AC = A.【点睛】本题主要考查利用空间向量求线段的长，考查向量数量积的运算法则，属于中档题.向量数量积的运算主要掌握两点：一是数量积的基本公式cos a b a b θ⋅=；二是向量的平方等于向量模的平方22a a =. 5．A解析：A【分析】建立空间直角坐标系，求出向量AM 与1BC 的向量坐标，利用数量积求出异面直线A M 与1B C 所成角的余弦值.【详解】 以D 为坐标原点，建立空间直角坐标系，如图所示：设正方体的棱长为1，则(1,0,0)A ，1(1,0,1)A ，(1,1,0)B ，1(1,1,1)B ，(0,1,0)C ∵M 为11A B 的中点 ∴1(1,,1)2M ∴1(0,,1)2AM =，52AM =；1(1,0,1)B C =--，12B C =. ∴异面直线A M 与1B C 所成角的余弦值为111110cos ,10AM B C AM B C AM B C⋅===⋅ 故选A.【点睛】本题主要考查异面直线所成的角的定义和求法，找出两异面直线所成的角∠AEM （或其补角），是解题的关键．如果异面直线所成的角不容易找，则可以通过建立空间直角坐标系，利用空间向量来求解．6．B解析：B【解析】设菱形中横向单位向量为,m 纵向单位向量为n ，则111,1122m n m n ==⋅=⨯⨯=，2a AB m n ==+，32b CD m n ==-+，()()232a b m n m n ⋅=+-+=223443421m n m n -+-⋅=-+-=-，故选B. 7．D解析：D 【分析】试题分析：结合其空间立体图形易知，112222=⨯⨯=S ，2312222S S ==⨯⨯=，所以23S S =且13S S ≠，故选D ．考点：空间直角坐标系及点的坐标的确定，正投影图形的概念，三角形面积公式． 8．C 解析：C【分析】建立空间直角坐标系，写出点的坐标，设出动点的坐标，利用向量的坐标公式求出向量坐标，利用向量垂直的充要条件列出方程求出动点P 的轨迹方程，得到P 的轨迹是底面圆的弦，利用勾股定理求出弦长．【详解】建立空间直角坐标系．设A （0，﹣1，0），B （0，1，0），S （0，03M （0，0，3P （x ，y ，0）． 于是有AM =（0，13MP =（x ，y ，3 由于AM ⊥MP ，所以（0，13•（x ，y ，30， 即y 34=，此为P 点形成的轨迹方程，其在底面圆盘内的长度为2371()4-=．故选C ．【点睛】本题考查通过建立坐标系，将求轨迹问题转化为求轨迹方程、考查向量的数量积公式、向量垂直的充要条件、圆的弦长的求法．属中档题9．D解析：D【分析】建立空间直角坐标系，找到平面1B EF 的法向量，利用向量法求点到平面的距离求解即可.【详解】以1D 为坐标原点，分别以11D A ，11D C ，1D D 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，则1(2,2,0)B ，1(0,2,0)C ，(2,1,2)E ，(1,2,2)F .设平面1B EF 的法向量为(,,)n x y z =，1(0,1,2)B E =-1(1,0,2)B F =-则1100n B E n B F ⎧⋅=⎪⎨⋅=⎪⎩，即2020y z x z -+=⎧⎨-+=⎩ 令1z =，得(2,2,1)n =.又11(2,0,0)BC =-，∴点1C 到平面1B EF 的距离1122|||2200|43||221n B C h n ⋅-⨯++===++， 故选：D .【点睛】 本题用向量法求点到平面的距离，我们也可以用等体积法求点到平面的距离，当然也可以找到这个垂线段，然后放在直角三角形中去求.10．C解析：C【分析】若要使MN 最短，点N 必须落在平面ABCD 内，且一定在DN 的连线上，此时应满足,,,D N M Q 四点共线，通过几何关系即可求解【详解】如图，当点N 落在平面ABCD 内，且,,,D N M Q 四点共线时，MN 距离应该最小，由PM 5=1MQ =，即点M 在以Q 为圆心，半径为1的圆上，由几何关系求得5DQ ，1DN MQ ==，故552NM DN MQ -=故答案选：C【点睛】本题考查由几何体上的动点问题求解两动点间距离的最小值，属于中档题11．B解析：B【分析】如图建立空间直角坐标系，可证明1A D ⊥平面11ABC D ，故平面11ABC D 的一个法向量为：1DA ，利用点到平面距离的向量公式即得解. 【详解】如图建立空间直角坐标系，则：1111(,,1),(0,0,1),(1,0,0),(1,1,0),(0,1,1)22O D A B C 111(,,0)22OD ∴=-- 由于AB ⊥平面111,ADD A AD ⊂平面11ADD A1AB A D ∴⊥，又11AD A D ⊥，1AB AD1A D ∴⊥平面11ABC D故平面11ABC D 的一个法向量为：1(1,0,1)DA = O ∴到平面11ABC D 的距离为： 1111||22||2OD DA d DA ⋅===故选：B【点睛】本题考查了点到平面距离的向量表示，考查了学生空间想象，概念理解，数学运算的能力，属于中档题.12．D解析：D 【分析】作AC x ⊥轴于C ，BD x ⊥轴于D ，则AB AC CD DB =++，两边平方后代入数量积即可求得2||AB ，则AB 的长可求．【详解】如图，()2,3A -，()3,2B -，作AC x ⊥轴于C ，BD x ⊥轴于D ，则()2,0C -，()3,0D ，3AC ∴=，5CD =，2DB =，沿x 轴把坐标平面折成60︒的二面角，CA ∴<，60DB >=︒，且0AC CD CD DB ⋅=⋅=，222||()AB AB AC CD DB ∴==++ 222222AC CD DB AC CD CD DB AC DB =+++⋅+⋅+⋅19254232322⎛⎫=+++⨯⨯⨯-= ⎪⎝⎭． 42AB ∴=即AB 的长为42故选：D ．【点睛】本题主要考查了空间角，向量知识的运用，考查学生的计算能力，属于中档题． 二、填空题13．【分析】由题意结合重心的性质和平面向量的三角形法则整理计算即可求得最终结果【详解】如图取BC 的中点F 连结DF 则∴【点睛】本题主要考查空间向量的运算法则及其应用意在考查学生的转化能力和计算求解能力 解析：0【分析】由题意结合重心的性质和平面向量的三角形法则整理计算即可求得最终结果.【详解】如图，取BC 的中点F ，连结DF ，则23DF DE =， ∴1322AB BC DE AD +--AB BF DF DA =+-+AF FD DA =++0=.【点睛】本题主要考查空间向量的运算法则及其应用，意在考查学生的转化能力和计算求解能力. 14．【解析】连结A1B ∵AA1⊥面ABC 平面A1B1C1∥面ABC ∴AA1⊥平面A1B1C1∵A1C1⊂平面A1B1C1∴AA1⊥A1C1∵△ABC 与△A1B1C1是全等三角形AB ⊥AC ∴A1B1⊥A1 解析：2π 【解析】连结A 1B ，∵AA 1⊥面ABC ，平面A 1B 1C 1∥面ABC ，∴AA 1⊥平面A 1B 1C 1，∵A 1C 1⊂平面A 1B 1C 1，∴AA 1⊥A 1C 1，∵△ABC 与△A 1B 1C 1是全等三角形，AB ⊥AC ，∴A 1B 1⊥A 1C 1，∵A 1B 1∩AA 1=A 1，∴A 1C 1⊥平面AA 1B 1B ，又∵AB 1⊂平面AA 1B 1B ，∴A 1C 1⊥AB 1，∵矩形AA 1B 1B 中，AA 1=AB ，∴四边形AA 1B 1B 为正方形，可得A 1B ⊥AB 1，∵A 1B∩A 1C 1=A 1，∴AB 1⊥平面A 1BC 1，结合BC 1⊂平面A 1BC 1，可得AB 1⊥BC 1，即异面直线AB 1与BC 1所成角为2π． 故答案为2π．15．【解析】∵向量与是共线向量∴∴或∵∴即∴则∴故答案为解析：22【解析】∵向量(21,3)a m =+与(2,)b m =是共线向量∴(21)6m m +=∴32m =或2m =- ∵0a b ⋅<∴(21)230m m +⨯+<，即27m <-∴2m =-，则(2,2)b =-∴22(b =+=故答案为16．【解析】由平行四边形中对角线互相平分的性质知AC 的中点即为BD 的中点AC 的中点设D(xyz)则∴x ＝5y ＝13z ＝－3故D(513－3)解析：(5,13,3)-【解析】由平行四边形中对角线互相平分的性质知，AC 的中点即为BD 的中点，AC 的中点7(,4,1)2O - ，设D (x ，y ，z )， 则7251,4,12222x y z +-++==-= ∴x ＝5，y ＝13，z ＝－3，故D (5,13，－3)．17．【分析】以点为坐标原点所在直线分别为轴建立空间直角坐标系利用空间向量法计算出异面直线的公垂线的长度即为所求【详解】由题意可知线段长度的最小值为异面直线的公垂线的长度如下图所示以点为坐标原点所在直线分解析：13【分析】以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系，利用空间向量法计算出异面直线1C D 、AC 的公垂线的长度，即为所求.【详解】由题意可知，线段PQ 长度的最小值为异面直线1C D 、AC 的公垂线的长度.如下图所示，以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系，则点()1,0,0A 、()0,1,0C 、()10,1,2C 、()0,0,0D ，所以，()1,1,0AC =-，()10,1,2=DC ，()1,0,0DA =，设向量(),,n x y z =满足n AC ⊥，1⊥n DC ，由题意可得1020n AC x y n DC y z ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，解得2x y y z =⎧⎪⎨=-⎪⎩，取2y =，则2x =，1z =-， 可得()2,2,1n =-， 因此，min 23DA n PQ n ⋅==. 故答案为：23. 【点睛】 关键点点睛：解本题的关键在于将PQ 长度的最小值转化为异面直线AC 、1C D 的距离，实际上就是求出两条异面直线的公垂线的长度，利用空间向量法求出两条异面直线间的距离，首先要求出两条异面直线公垂线的一个方向向量的坐标，再利用距离公式求解即可. 18．【解析】∵∴∴故答案为解析：111,,633【解析】∵ O G OM MG =+，12OM OA =，2 ,3MG MN MN ON OM ==-，1 ()2ON OB OC =+，∴111 633OG OA OB OC =++，∴16x =，13y z ==，故答案为111,,63319．【解析】距离【解析】距离d ==20．【解析】分析：设的中点为连接由余弦定理可得利用三角函数的有界性可得结果详解：设的中点为连接则是二面角的平面角可得在三角形中由余弦定理可得即的取值范围是为故答案为点睛：本题主要考查空间两点的距离余弦定解析：)【解析】分析：设AB 的中点为D ，连接,,VD CD VC ，由余弦定理可得22233cos 22VC a a VDC =-∠，利用三角函数的有界性可得结果. 详解：设AB 的中点为D ，连接,,VD CD VC ，则VD VC == VDC ∠是二面角V AB C --的平面角，可得0,1cos 1VDC VDC π<∠<-<∠<，在三角形VDC 中由余弦定理可得，2222cos VC VDC ⎫⎫=+-∠⎪⎪⎪⎪⎝⎭⎝⎭ 2233cos 22a a VDC =-∠22030VC a VC <<⇒<<，即VC 的取值范围是()，为故答案为().点睛：本题主要考查空间两点的距离、余弦定理的应用，意在考查空间想象能力、数形结合思想的应用，属于中档题. 三、解答题21．答案见解析【分析】先利用已知条件写出点坐标，设(0,,2)(02),(,2,2)(02)E a a F b b ≤≤≤≤，进而得到1,,,EF A A F C E B 的坐标，利用空间向量数量积的坐标表示求出1,EF A AE BF C ⋅⋅；若选① ：利用空间向量数量积的坐标表示公式、空间向量垂直的性质即可求解；若选② ：利用空间向量模的坐标表示公式即可得出结果；若选③ ：利用空间向量夹角的性质进行求解即可.【详解】解：由题意，正方体1111ABCD A BC D -棱长为2，则1(2,0,0),(2,2,0),(2,0,2),(0,0,0),(0,2,0)A B A D C ，设(0,,2)(02),(,2,2)(02)E a a F b b ≤≤≤≤，则1(,2,0),(2,2,2),(2,,2),(2,0,2)EF b a A AE a BF b C =-=--=-=-， 所以142(),82EF A a b AE C BF b ⋅=-+⋅=-.选择①：()()DE CF DE CF +⊥-，所以22()()0,DE CF DE CF DE CF +⋅-==，得a b =，若10EF AC ⋅=得42()0a b -+=， 则1a b ==，故存在点(0,1,2),(1,2,2)E F ，满足10EF AC ⋅=，826AE BF b ⋅=-=. 选择②：因为17||2DE =，=， 得12a =， 若10EF AC ⋅=， 即42()0a b -+=，得32b =. 故存在点130,,2,,2,222E F ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭， 满足10EF AC ⋅=，825AE BF b ⋅=-=. 选择③：因为0cos ,1EF DB <〈〉<，所以EF 与DB 不共线，所以2b a ≠-，即2a b +≠，则142()0EF AC a b ⋅=-+≠，故不存在点,E F 满足10EF AC ⋅=. 【点睛】关键点睛：建立空间坐标系，利用空间向量数量积的坐标表示、空间向量垂直的性质、空间向量模的坐标表示公式以及空间向量夹角的性质是解决本题的关键.22．（1）详见解析；（2）66. 【分析】（1）根据四边形ABB 1A 1和ADD 1A 1均为正方形，得到11,AA AB AA AD ⊥⊥，再由线面垂直的判定定理证得1AA ⊥平面ABCD ，然后利用面面垂直的判定定理证明.（2）以A 为原点，以1,,AB AD AA 分别为x ,y ,z 轴，建立空间直角坐标系,求得平面1BCD 的一个法向量为(),,m x y z =，又平面CDA 的一个法向量为()0,0,1n =，然后由cos ,m n m n m n ⋅=⋅求解.【详解】 （1）因为四边形ABB 1A 1和ADD 1A 1均为正方形.所以11,,AA AB AA AD AB AD A ⊥⊥⋂=，所以1AA ⊥平面ABCD ；又因为1AA ⊂平面ABB 1A 1，所以平面ABB 1A 1平面ABCD ；（2）以A 为原点，以1,,AB AD AA 分别为x ,y ,z 轴，建立空间直角坐标系：则()()()()10,0,0,2,1,0,0,2,0,2,0,2A C D B ，所以()()12,1,0,0,1,2CD CB =-=-，设平面1BCD 的一个法向量为(),,m x y z =， 则100m CD m CB ⎧⋅=⎪⎨⋅=⎪⎩，即2020x y y z -+=⎧⎨-+=⎩， 令1,2,1x y z ===，则()1,2,1m =，又平面CDA 的一个法向量为()0,0,1n =，所以16cos ,66m nm n m n ⋅===⋅， 二面角B 1CD-A 的余弦值是66【点睛】 方法点睛：求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．23．（1）证明见解析；（2）2211. 【分析】（1）取SC 的中点F ，连接,DF EF ，证明四边形ADFE 为平行四边形，可得//AE DF ，即可证//AE 平面SCD ；（2）建立如图所示空间直角坐标系，然后写出各点坐标，得平面ABE 的法向量为AD ，计算平面ACE 的法向量m ，利用数量积公式代入计算二面角的余弦值.【详解】（1）证明：取SC 的中点F ，连接,DF EF因为E 、F 为SB 、SC 的中点，所以//EF BC 且132EF BC ==，又因为//AD BC ，3AD =，6BC =，所以//EF AD 且EF AD =，所以四边形ADFE 为平行四边形，所以//AE DF ，又AE ⊄平面SCD ，DF ⊂平面SCD ，所以//AE 平面SCD ． （2）因为SA ⊥平面ABCD ，AD AB ⊥，所以建立如图所示空间直角坐标系， 则(0,0,0),(4,0,0),(4,6,0),(0,3,0),(2,0,2)A B C D E ，(2,0,2),(4,0,0),(4,6,0)AE AB AC ===，(0,3,0)AD = 由题意可知AD ⊥平面ABE ，设平面ACE 的法向量(,,)m x y z =所以00AC m AE m ⎧⋅=⎨⋅=⎩，则460220x y x z +=⎧⎨+=⎩，得(3,2,3)m =-- 设二面角B AE C --的平面角为θ， 所以622cos cos ,322AD m θAD m AD m ⋅-====⨯，所以二面角B AE C --的余弦值为2211.【点睛】本题考查了立体几何中的线面平行的判定和二面角的求解问题，意在考查学生的空间想象能力和逻辑推理能力；解答本题关键在于能利用直线与直线、直线与平面关系的相互转化，通过中位线平行证明线线平行，同时对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.24．（1）证明见解析（2）22（3）155 【分析】(1)由PB PD =可得出PO BD ⊥，再由菱形性质可得AC BD ⊥，即可证明BD ⊥平面POC ，可得PC BD ⊥；（2）先证明OP ⊥平面ABCD ，可以O 为原点，以OB ，OC ，OP 为坐标轴建立空间直角坐标系，利用向量法求线面角；（3）由（2）利用向量法求二面角的余弦值.【详解】（1）设,AC BD 交点为O ,连接PO ，ABCD 是边长为2的菱形，,AC BD O ∴⊥是,AC BD 的中点，,PD O B BD P P =∴⊥，又PO ⊂平面POC ,AC ⊂平面 POC ，PO AC O =，BD ∴⊥平面POC ，PC ⊂平面POC ，.C BD P ∴⊥（2）60,2,A D B D A A B ︒===∠ABD ∴是等边三角形，又AB PB PD ==PBD ∴是等边三角形， 3P OA O ∴== 222OP PA OA +∴=，OA OP ∴⊥又,OP OB OA OB O ⊥⋂=OP ∴⊥平面ABCD ，以O 为原点，以OB ，OC ，OP 为坐标轴建立空间直角坐标系如图:则(1,0,0),3,0),3)B C P ，(0,3,3PC ∴=-，而3,0)OC →=是平面 PBD 的一个法向量，设直线PC 与平面PBD 所成角为θ， 则||2sin 263|||||PC OC PC OC θ→→→→⋅===⋅ 所以直线PC 与平面PBD 所成角的正弦值为22. (3)由（2）知(3,0)BC →=-,(3,3PC =-设平面BPC 的法向量n (x,y,z)→=， 则.0.0n PC n BC ⎧=⎨=⎩,33030y z x y ⎧-=⎪∴⎨-+=⎪⎩, 令1y =，得3,1x z ==，所以(3,1,1)n →=，又BD ⊥平面EPC , (1,0,0)m ∴=是平面 EPC 的一个法向量，315cos ,||||515m n m n m n ⋅∴〈〉===⋅⋅， ∴二面角B PC E --的余弦值为155. 【点睛】关键点点睛：根据题目所给条件，利用平面几何知识证明OA OP ⊥，再根据OP OB ⊥，证明OP ⊥平面ABCD ，得以O 为原点，以OB ，OC ，OP 为坐标轴建立空间直角坐标系是解题的关键所在.25．（1）点M 在CE 的中点处，证明见解析；（2）32. 【分析】（1）首先观察图形的特征，确定点M 的位置，之后利用线面平行的判定定理证明即可； （2）建立空间直角坐标系，设出边长，写出点的坐标，利用向量法求得线面角的正弦值.【详解】（1）点M 在CE 的中点处，证明如下：取BC 中点P ，连接,BP AP ，根据题意，可知//,PM AF PM AF =，所以四边形AFMP 是平行四边形，所以//AP MF ，又因为FM ⊄平面ABCD ，AP ⊂平面ABCD ，所以//MF 平面ABCD ；（2）设1AF AB AD ===，如图建立空间直角坐标系，则有1(1,0,1),(1,1,0),(0,1,),(0,0,0)2D F M B ，所以(0,1,1)DF =-，1(1,1,0),(0,1,)2BF BM ==，设平面BFM 的法向量为(,,)n x y z =， 则有00n BF n BM ⎧⋅=⎨⋅=⎩，即0102x y y z +=⎧⎪⎨+=⎪⎩，取1y =，则有1,2x z =-=-， 所以平面BFM 的一个法向量为(1,1,2)n =--， 所以03cos ,26DF nDF n DF n ⋅+<>===⋅， 所以直线DF 与平面BFM 3 【点睛】 思路点睛：该题考查的是有关立体几何的问题，解题思路如下：（1）首先根据图形的特征，判断出点的位置，之后利用线面平行的判定定理证明即可； （2）在证明的过程中，注意线在面外和线在面内的条件；（3）建立空间直角坐标系，求得平面的法向量和直线的方向向量；（4）利用向量所成角的余弦值得到线面角的正弦值.26．（Ⅰ）证明见解析；（Ⅱ）3913. 【分析】（Ⅰ）取AD 的中点G ，连结PG 、GB 、BD ，根据PA PD =和ABD △是正三角形，证明AD ⊥平面PGB 即可.（Ⅱ）根据侧面PAD ⊥底面ABCD ，PG AD ⊥，易得直线GA 、GB 、GP 两两互相垂直，以G 为原点，直线GA 、GB 、GP 所在直线为x 轴、y 轴和z 轴建立空间直角坐标系G xyz -，求得平面PBC 的一个法向量()000,,n x y z =，再由平面PAD 的一个法向量1(0,3,0)n GB a ==，设平面PAD 与平面PBC 所成锐二面角为θ，由11cos ||n n n n θ⋅=⋅求解. 【详解】（Ⅰ）如图所示：取AD 的中点G ，连结PG 、GB 、BD ．PA PD =，PG AD ∴⊥AB AD =，且60DAB ∠=︒，ABD ∴是正三角形，BG AD ⊥，又PG BG G =，AD ∴⊥平面PGB ．AD PB ∴⊥（Ⅱ）∵侧面PAD ⊥底面ABCD ，又PG AD ⊥，PG ∴⊥底面ABCD ．PG BG ∴⊥．∴直线GA 、GB 、GP 两两互相垂直，故以G 为原点，直线GA 、GB 、GP 所在直线为x 轴、y 轴和z 轴建立如图所示的空间直角坐标系G xyz -．设PG a =，则可求得(0,0,)P a ，(,0,0)A a ，3,0)B a ，(,0,0)D a -，33,02C a ⎛⎫- ⎪ ⎪⎝⎭． 33,,02BC a ⎛⎫∴=- ⎪ ⎪⎝⎭．(0,3,)PB a a ∴=-． 设()000,,n x y z =是平面PBC 的一个法向量，则0n BC ⋅=且0n PB ⋅=．0000330,230.ax ay az ⎧-=⎪∴⎪-=⎩解得00003,3.x y z y ⎧=⎪⎨⎪=⎩ 取03y =(1,3,3)n =-．又∵平面PAD 的一个法向量13,0)n GB a ==，设平面PAD 与平面PBC 所成锐二面角为θ， 则1139cos ||1393n n n n aθ⋅===⋅++⋅ 所以平面PAD 与平面PBC 39 【点睛】 方法点睛：求二面角最常用的方法：1、几何法：二面角的大小用它的平面角来度量．平面角的作法常见的有①定义法；②垂面法．注意利用等腰、等边三角形的性质．向量法：分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．。

本文档中所有公式在Word中均能正常显示！！！北师大版高中数学选修2-1《圆锥曲线与方程》测验（附答案）(时间:120分钟满分:150分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.方程x2+(x2+y2-1)2=0所确定的曲线是()A.y轴或圆B.两点(0,1)与(0,-1)C.y轴或直线y=±1D.以上都不正确2.如图,已知圆O的方程为x2+y2=100,点A(-6,0),M为圆O上任一点,AM的垂直平分线交OM于点P,则点P的轨迹是()A.圆B.抛物线C.椭圆D.两条直线3.双曲线=1(mn≠0)的离心率为2,有一个焦点与抛物线y2=4x的焦点重合,则mn的值为()A. B. C. D.4.若抛物线y2=4x上一点P到焦点F的距离为10,则P点坐标为()A.(9,6)B.(9,±6)C.(6,9)D.(6,±9)5.以双曲线=-1的焦点为顶点,顶点为焦点的椭圆方程为()A.=1B.=1C.=1D.=16.若点P是以F1,F2为焦点的椭圆=1(a>b>0)上一点,且=0,tan∠PF1F2=,则此椭圆的离心率e=()A. B. C. D.7.已知双曲线=1(a>0,b>0)的一条渐近线为y=kx(k>0),离心率e=k,则双曲线方程为()A.=1B.=1C.=1D.=18.抛物线y=x2上到直线2x-y-4=0的距离最近的点的坐标是()A. B.(1,1)C. D.(2,4)9.已知点M(-3,0),N(3,0),B(1,0),动圆C与直线MN相切于点B,过M,N与圆C相切的两直线相交于点P,则点P的轨迹方程为()A.x2-=1(x>1)B.x2-=1(x<-1)C.x2+=1(x>0)D.x2-=1(x>1)10.若点P为共焦点的椭圆C1和双曲线C2的一个交点,F1,F2分别是它们的左、右焦点,设椭圆的离心率为e1,双曲线的离心率为e2,若=0,则= ()A.1B.2C.3D.411.设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB 的面积为()A. B. C. D.12.在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L-距离”定义为||P1P2|=|x1-x2|+|y1-y2|,则平面内与x轴上两个不同的定点F1,F2的“L-距离”之和等于定值(大于||F1F2|)的点的轨迹可以是()二、填空题(本大题共4个小题,每小题5分,共20分.把答案:填在题中的横线上)13.平面上一机器人在行进中始终保持与点F(1,0)的距离和到直线x=-1的距离相等.若机器人接触不到过点P(-1,0)且斜率为k的直线,则k的取值范围是.14.设中心在原点的椭圆与双曲线2x2-2y2=1有相同的焦点,且它们的离心率互为倒数,则该椭圆的方程是.15.在抛物线y2=16x内,通过点M(2,4)且在此点被平分的弦所在直线方程是.16.已知双曲线C1:=1(a>0,b>0)与双曲线C2:=1有相同的渐近线,且C1的右焦点为F(,0),则a=,b=.三、解答题(本大题共6个小题,共70分.解答时应写出文字说明、证明过程或演算步骤)17.(满分10分)已知双曲线的中心在原点,焦点F1,F2在坐标轴上,一条渐近线方程为y=x,且过点(4,-).(1)求双曲线方程;(2)若点M(3,m)在此双曲线上,求.18.(满分12分)如图,已知抛物线C1:x2+by=b2经过椭圆C2:=1(a>b>0)的两个焦点.(1)求椭圆C2的离心率;(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.19.(满分12分)在平面直角坐标系xOy中,已知双曲线C:2x2-y2=1.(1)设F是C的左焦点,M是C右支上一点,若|MF|=2,求点M的坐标;(2)设斜率为k(|k|<)的直线l交C于P,Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ.20.(满分12分)已知椭圆C经过点A,两个焦点为(-1,0),(1,0).(1)求椭圆C的方程;(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.21.(满分12分)如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,=(-4,-12).(1)求直线l和抛物线C的方程;(2)抛物线上一动点P从点A到点B运动时,求△ABP面积的最大值.。

高二期末考试数学试题晁群彦一．选择题（每小题5分，满分６ 0分）１. 设l , m , n均为直线 ,其中m , n在平面a内 ,则“l”是“l m且 l的（）n ”A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件２. 对于两个命题：①x R,1sin x 1 ，② x2cos2，R , sin x x 1下列判断正确的是（）。

A.①假② 真B.① 真② 假C.①②都假D.①②都真３. 与椭圆x2y21共焦点且过点 Q (2,1)的双曲线方程是（）422222A. x 2y1B. xy 21 C.xy 21 D.x y124233４.已知F1, F2是椭圆的两个焦点，过F1且与椭圆长轴垂直的弦交椭圆与 A ,B 两点，则 ABF2是正三角形，则椭圆的离心率是（）w wwk 5u om21C 3D1A B33 22５. 过抛物线y28 x 的焦点作倾斜角为450直线 l ，直线 l 与抛物线相交与A，B两点，则弦 AB的长是（）A 8B16C32D64wwwk 5 u om６. 在同一坐标系中，方程222x21与 ax by2b0 ) 的曲线大致是（）a x b0( aA．B．C． D ．x 2y 2( a b >0)的两个焦点 F1，F2，点P在椭圆上，则P F1F2的面积７. 已知椭圆1最a 2b 2大值一定是（）Aa 2B a bC a a 2 b 2 Db a 2 b 2８. 已知向量a(1,1,0 ), b ( 1, 0, 2 ), 且 k a b 与 2 ab互相垂直 , 则实数 k 的值是 ()137A ． 1B ．5C ．5D ．5９ .在正方体 ABC DA 1B 1C 1D 1 中，E 是棱A 1B1的中点，则A 1B 与 D 1 E 所成角的余弦值为（）510510A ． 10B ． 10C ． 5D ． 5１０ .若椭圆 mx2ny 21(m0, n0)与直线y1 x交于 A ， B 两点 ,过原点与线段 AB 中点2n的连线的斜率为2 ，则m的值是 ()2 2B . 2C . 3D .2A.229１ １ . 过 抛 物 线 x 2 4 y 的 焦 点 F 作 直 线 交 抛 物 线 于 P 1 x 1 , y 1 , P 2 x 2 , y 2 两点，若 y 1y 26 ，则 P 1P 2 的值为 （）A ． 5 B．6 C． 8 D． 10１２ .以 x2y 2 =1 的焦点为顶点，顶点为焦点的椭圆方程为 （）412222222xy1xy1xy1 D.A.12B.16 C.4161216二．填空题（每小题４分）１３．已知 A 、B 、C三点不共线，对平面 ABC外一点 O ，给出下列表达式：OMx OAy OB1OC3其中 x ，y 是实数，若点 M 与 A 、 B 、 C 四点共面，则 x+y=___１４．斜率为 1 的直线经过抛物线y2＝4x 的焦点，且与抛物线相交于A,B 两点，则AB等于___１５．若命题 P ： “ x ＞ 0， ax2 2 x2”是真命题 ，则实数 a 的取值范围是 ___．１６．已知A O B90 ，C为空间中一点，且AO C BOC 60，则直线O C与平面AO B所成角的正弦值为 ___．三．解答题（解答应写出必要的文字说明、证明过程和演算步骤。

(选修2-1)孙敏、选择题（本大题共12小题，每小题6分，共72 分）1、a3>8 是a>2 的（）A .充分非必要条件要非充分条件B .必C.充要条件D.既非充分也非必要条件2、全称命题“所有被5整除的整数都是奇数”的否定是（）A. 所有被5整除的整数都不是奇数；B. 所有奇数都不能被5整除C. 存在一个被5整除的整数不是奇数；D. 存在一个奇数，不能被5整除1 23、抛物线y - x的准线方程是（）81 1A. xB. y 2C. yD. y 232 324、有下列命题：①ax2 bx c 0是一元二次方程（a 0）;②空集是任何集合的真子集；③若a R ,则a20 ;④若a,b R且ab 0 ,则a 0且b 0 .其中真命题的个数有（）A. 1B. 2C. 3D. 42 25、椭圆—y_ 1的离心率为（)25 163 r 34 r 9AA.-B. C D.5 4 5 256、以坐标轴为对称轴，以原点为顶点且过圆x2 y2 2x 6y 9 0的圆心的抛物线的方程是（)A . y 3x2或y 3x2B . y 3x2C . y 9x 或y 3x2 2 2D . y 3x 或y 9x7、已知a=（2，- 3，1）, b=（4，- 6, x），若a 丄b,则x 等于（定点M 与点A 、 B 、C 疋共面的疋（)uuuu UL UUU UUUrUU UUUUU UU U UU Ur A . OM OAOBOCB . OM 2O A OB OC UULU UL 1UU 1 UUUUUU U 1 UUU 1 UUU 1UUL C . OM OA —O—OC D .OM-OA -OB —233 3 310、设 a 3 ,b 6, 若a?）= 9,则 a, b等于 ( )A . 90°B .60°C .120°D.45°111、已知向量a =（ 1, 1,- 2）, b = 2,1,-，若a • b >0,则实数x 的取值 x范围为（）2 2A .（0,3）B . ©3]C .(,0) U [3,) D .(,0] U [3,)12、设 x 1 ,x 2 R ,常数 a 0 ,定义运算“* ”： X 1 2 2X 2 (X 1X 2) (X 1 X 2),若x 0,则动点P （x,. x a ）的轨迹是（ ）A .圆B .椭圆的一部分C .双曲线的一部分D .抛物线的一部分、填空题（本大题共5小题，每小题5分，共25分） 13、命题“若x 2 4x 3 0 ,贝U x = 1或x = 3 ”的逆否命题 为.14、给出下列四个命题：① x R ，是方程3x -5= 0的根；②x R,| x| 0 ; ③x R,x 21 :④ x R,都不是方程x2 3x 30的根.其中假命题的序号有 _________________ .A . —26B . — 10、如图，：空间四边形 ABCD 中，M 、则AB1BC1 =BD 等于（22A . ADB . GAC . AGD . MG9、已知 A 、B 、C 三点不共线，；C . 2D . 10ABC 外的任一点O ,下列条件中能确8G 分别是BC 、CD 的中点,2 215、若方程卫y 1表示的图形是双曲线，则k的取值范围2 k k 1为____________ •16、抛物线y2 4x的准线方程是_____________ .17、由向量a (1,0, 2) , b ( 1, 2, 1)确定的平面的一个法向量是n (x, y, 2)，贝U x= __________ , y= _________ .三、解答题(本大题共5小题，共53分.解答应写出文字说明、演算步骤或推证过程)18、(本小题满分8分)2 2双曲线的离心率等于2,且与椭圆0 二1有相同的焦点，求此双曲线方程.25 919、(本小题满分10分)已知命题P: “若ac 0,则二次方程ax2 bx c 0没有实根”(1) 写出命题P的否命题；(2) 判断命题P的否命题的真假，并证明你的结论.20、(本小题满分11分)已知ab 0,求证a b 1的充要条件是a 3 b 3 ab a 2 b 2 021、(本小题满分12分)如图，在正方体ABCD — A i B i C i D i 中，E 、F 分 别是BB i 、CD 的中点.(I)证明：AD 丄 D i F ; (U)求AE 与D i F 所成的角；(川)证明：面 AED 丄面A i FD i .22、(本小题满分i2分)2 2设椭圆务+占 i (a >b >0)的左焦点为F i ( — 2, 0),左准线L i : x 兰与 a bcx 轴交于点N ( — 3, 0),过点N 且倾斜角为300的直线L 交椭圆于A 、B 两点。

选修〔 2-1 〕学刘理论班级：姓名： 座号： 成绩：一、选择题〔15× 4=60 分〕1、(x+1)(x+2)>0是 (x+1)(x 2 +2)>0的〔〕条件A必要不充分 B充要C充分不必要 D 既不充分也不必要2、 p 是 r 的充分不必要条件， s 是 r 的必要条件， q 是 s 的必要条件，那么 p 是 q 成立的〔 〕条件A 必要不充分B 充分不必要C 充要D 既不充分也不必要 uuur uuur3、 A 2, 5,1, B 2, 2,4 ,C 1,4,1 ，那么向量 AB 与 AC 的夹角为〔〕A 300B450C600D9004、O 、A 、B 、C 为空间四个点，又 OA、OB、OC为空间的一个基底，那么〔〕A O 、 A 、B 、C 四点共线 B O 、A 、B 、C 四点共面C O 、A 、B 、C 四点中任三点不共线D O 、A 、B 、C 四点不共面5、给出以下关于互不相同的直线 m 、 l 、 n 和平面α、β的四个命题：①假设m, lA,点 Am ,那么 l 与 m 不共面；②假设m 、l 是异面直线， l // , m //,且 n l , nm ,那么 n；③假设l //, m //, // , 那么 l // m ；④假设l, m, lm点 A, l // , m // , 那么 // .其中为假命题的是 〔 〕A ①B ②C ③D ④6、高为 3 的直棱柱 ABC — A ′ B ′ C ′的底面是边长为 1 的正三角形〔如图 1 所示〕，那么三棱锥 B ′— ABC 的体积为〔 〕A1B1C3 D 342647、假设焦点在 x轴上的椭圆 x2y 2 1 的离心率为 1，那么 m=〔 〕2m2A3B 3C8D2 2338、 P3cos,3sin,1 和Q2cos,2sin,1 ，那么 PQ 的取值范围是〔〕A1,5B1,5C0,5D0,259、椭圆x2y 21上一点 P 到它的右准线的距离为10, 那么点 P 到它的左焦10036点的距离是 ()A 8B 10C 12D 1410、与双曲线x2y21有共同的渐近线,且经过点 3,2 3 的双曲线的一个焦点916到一条渐近线的距离是 () A 1 B2 C 4 D 811、假设抛物线y28x 上一点P到准线和抛物线的对称轴的距离分别为10和6，那么此点 P 的横坐标为〔〕A 10B9C8D非上述答案12、坐标满足方程F〔 x， y〕 =0 的点都在曲线 C上，那么〔〕A 曲线 C上的点的坐标都适合方程F〔 x， y〕=0；B凡坐标不适合 F〔x，y〕=0 的点都不在 C上；C不在 C上的点的坐标不必适合 F〔x，y〕=0；D不在 C上的点的坐标有些适合 F〔x，y〕=0，有些不适合 F〔 x， y〕 =0。