九年级数学下册解题技巧专题解决抛物线中与系数a,b,c有关的问题课件(新版)北师大版

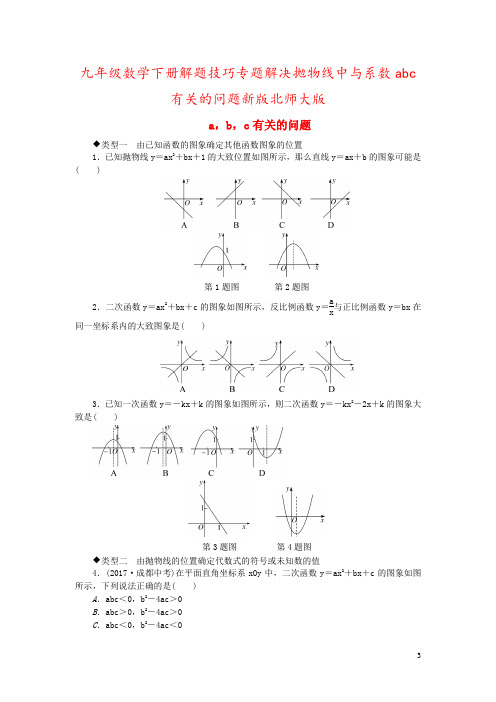
九年级数学下册解题技巧专题解决抛物线中与系数abc有关的问题新版北师大版a ，b ，c 有关的问题◆类型一 由已知函数的图象确定其他函数图象的位置1．已知抛物线y ＝ax 2＋bx ＋1的大致位置如图所示，那么直线y ＝ax ＋b 的图象可能是( )第1题图 第2题图2．二次函数y ＝ax 2＋bx ＋c 的图象如图所示，反比例函数y ＝a x 与正比例函数y ＝bx 在同一坐标系内的大致图象是( )3．已知一次函数y ＝－kx ＋k 的图象如图所示，则二次函数y ＝－kx 2－2x ＋k 的图象大致是( )第3题图 第4题图◆类型二 由抛物线的位置确定代数式的符号或未知数的值4．(2017·成都中考)在平面直角坐标系xOy 中，二次函数y ＝ax 2＋bx ＋c 的图象如图所示，下列说法正确的是( )A ．abc ＜0，b 2－4ac ＞0B ．abc ＞0，b 2－4ac ＞0C ．abc ＜0，b 2－4ac ＜0D．abc＞0，b2－4ac＜05．已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，则下列结论中正确的是( ) A．a＞0B．c＜0C．3是方程ax2＋bx＋c＝0的一个根D．当x＜1时，y随x的增大而减小第5题图第6题图6．(2017·烟台中考)二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，对称轴是直线x ＝1，下列结论：①ab＜0；②b2＞4ac；③a＋b＋2c＜0；④3a＋c＜0.其中正确的是( ) A．①④B．②④C．①②③ D．①②③④7．(2017·营口一模)函数y＝x2＋bx＋c与y＝x的图象如图所示，有以下结论：①b2－4c＞0；②b＋c＋1＝0；③3b＋c＋6＝0；④当1＜x＜3时，x2＋(b－1)x＋c＜0.其中正确的是________(填序号)．8．二次函数y＝ax2＋bx＋c的图象如图所示，且P＝|2a＋b|＋|3b－2c|，Q＝|2a－b|－|3b＋2c|，比较P，Q的大小关系．参考答案与解析1．A2．C 解析：由y ＝ax 2＋bx ＋c 的图象开口向下，对称轴在y 轴右侧，得a ＜0，－b2a ＞0，∴b ＞0，∴反比例函数y ＝a x的图象位于第二、四象限，正比例函数y ＝bx 的图象位于第一、三象限．故选C.3．B 解析：由一次函数的图象可知k ＞1，∴－k ＜0，－1<－1k<0，∴抛物线开口向下，对称轴在直线x ＝－1与y 轴之间，与y 轴的交点在(0，1)的上方．故选B.4．B 5.C 6.C7．③④ 解析：∵二次函数y ＝x 2＋bx ＋c 与x 轴无交点，∴b 2－4ac ＜0，故①错误；当x ＝1时，y ＝1＋b ＋c ＝1，故②错误；∵当x ＝3时，y ＝9＋3b ＋c ＝3，∴3b ＋c ＋6＝0，故③正确；∵当1＜x ＜3时，二次函数值小于一次函数值，∴x 2＋bx ＋c ＜x ，∴x 2＋(b －1)x ＋c ＜0，故④正确．故正确的为③④.8．解：∵抛物线的开口向下，对称轴在y 轴右侧，∴a ＜0，－b2a＞0，∴b ＞0，∴2a－b ＜0.∵－b 2a ＝1，∴2a ＋b ＝0，a ＝－12b .当x ＝－1时，y ＝a －b ＋c ＜0，∴－12b －b ＋c＜0，∴3b －2c ＞0.∵抛物线与y 轴的正半轴相交，∴c ＞0，∴3b ＋2c ＞0，∴P ＝|2a ＋b |＋|3b －2c |＝3b －2c ，Q ＝|2a －b |－|3b ＋2c |＝b －2a －3b －2c ＝－2a －2b －2c ，∴Q －P ＝－2a －2b －2c －3b ＋2c ＝－2a －5b ＝－4b ＜0，∴P ＞Q .。

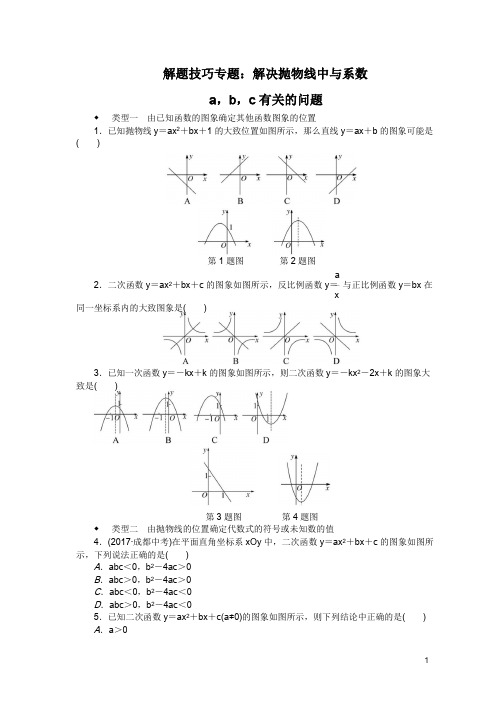
解题技巧专题：解决抛物线中与系数a ，b ，c 有关的问题◆ 类型一 由已知函数的图象确定其他函数图象的位置1．已知抛物线 y ＝ax 2＋bx ＋1 的大致位置如图所示，那么直线 y ＝ax ＋b 的图象可能是( )第 1 题图 第 2 题图a2．二次函数 y ＝ax 2＋bx ＋c 的图象如图所示，反比例函数 y ＝与正比例函数 y ＝bx 在 x同一坐标系内的大致图象是( )3．已知一次函数 y ＝－kx ＋k 的图象如图所示，则二次函数 y ＝－kx 2－2x ＋k 的图象大 致是( )第 3 题图 第 4 题图◆ 类型二 由抛物线的位置确定代数式的符号或未知数的值4．(2017·成都中考)在平面直角坐标系 xOy 中，二次函数 y ＝ax 2＋bx ＋c 的图象如图所 示，下列说法正确的是( )A ．abc ＜0，b 2－4ac ＞0B ．abc ＞0，b 2－4ac ＞0C ．abc ＜0，b 2－4ac ＜0D ．abc ＞0，b 2－4ac ＜05．已知二次函数 y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，则下列结论中正确的是( ) A ．a ＞01B．c＜0C．3 是方程ax2＋bx＋c＝0 的一个根D．当x＜1 时，y 随x 的增大而减小第5 题图第6 题图6．(2017·烟台中考)二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，对称轴是直线x＝1，下列结论：①ab＜0；②b2＞4ac；③a＋b＋2c＜0；④3a＋c＜0.其中正确的是() A．①④B．②④C．①②③D．①②③④7．(2017·营口一模)函数y＝x2＋bx＋c 与y＝x 的图象如图所示，有以下结论：①b2－4c ＞0；②b＋c＋1＝0；③3b＋c＋6＝0；④当1＜x＜3 时，x2＋(b－1)x＋c＜0.其中正确的是________(填序号)．8．二次函数y＝ax2＋bx＋c 的图象如图所示，且P＝|2a＋b|＋|3b－2c|，Q＝|2a－b|－|3b ＋2c|，比较P，Q 的大小关系．参考答案与解析1．A2b 2．C解析：由y＝ax2＋bx＋c的图象开口向下，对称轴在y轴右侧，得a＜0，－＞2aa0，∴b＞0，∴反比例函数y＝的图象位于第二、四象限，正比例函数y＝bx的图象位于第x一、三象限．故选C.13．B解析：由一次函数的图象可知k＞1，∴－k＜0，－1<－<0，∴抛物线开口向下，k对称轴在直线x＝－1 与y轴之间，与y轴的交点在(0，1)的上方．故选B.4．B 5.C 6.C7．③④解析：∵二次函数y＝x2＋bx＋c与x轴无交点，∴b2－4ac＜0，故①错误；当x＝1 时，y＝1＋b＋c＝1，故②错误；∵当x＝3 时，y＝9＋3b＋c＝3，∴3b＋c＋6＝0，故③正确；∵当1＜x＜3 时，二次函数值小于一次函数值，∴x2＋bx＋c＜x，∴x2＋(b－1)x＋c＜0，故④正确．故正确的为③④.b8．解：∵抛物线的开口向下，对称轴在y轴右侧，∴a＜0，－＞0，∴b＞0，∴2a－2ab 1 1b＜0.∵－＝1，∴2a＋b＝0，a＝－b.当x＝－1 时，y＝a－b＋c＜0，∴－b－b＋c＜0，2a 2 2∴3b－2c＞0.∵抛物线与y轴的正半轴相交，∴c＞0，∴3b＋2c＞0，∴P＝|2a＋b|＋|3b－2c|＝3b－2c，Q＝|2a－b|－|3b＋2c|＝b－2a－3b－2c＝－2a－2b－2c，∴Q－P＝－2a－2b－2c－3b＋2c＝－2a－5b＝－4b＜0，∴P＞Q.3。

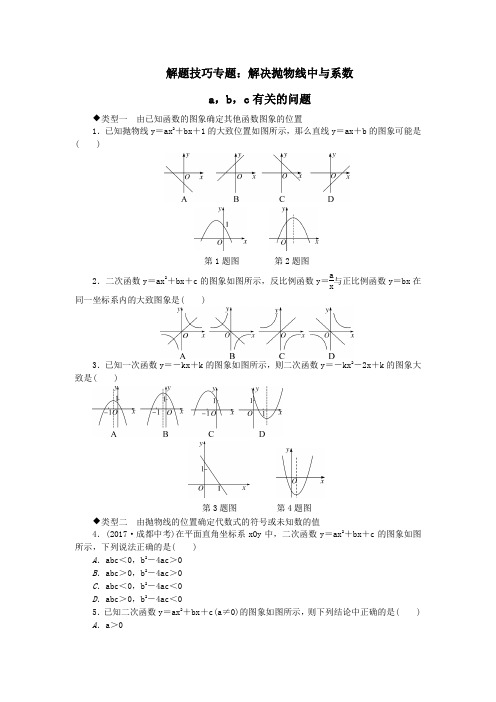
解题技巧专题：解决抛物线中与系数a ，b ，c 有关的问题◆类型一 由已知函数的图象确定其他函数图象的位置1．已知抛物线y ＝ax 2＋bx ＋1的大致位置如图所示，那么直线y ＝ax ＋b 的图象可能是( )第1题图 第2题图2．二次函数y ＝ax 2＋bx ＋c 的图象如图所示，反比例函数y ＝a x 与正比例函数y ＝bx 在同一坐标系内的大致图象是( )3．已知一次函数y ＝－kx ＋k 的图象如图所示，则二次函数y ＝－kx 2－2x ＋k 的图象大致是( )第3题图 第4题图◆类型二 由抛物线的位置确定代数式的符号或未知数的值4．(2017·成都中考)在平面直角坐标系xOy 中，二次函数y ＝ax 2＋bx ＋c 的图象如图所示，下列说法正确的是( )A ．abc ＜0，b 2－4ac ＞0B ．abc ＞0，b 2－4ac ＞0C ．abc ＜0，b 2－4ac ＜0D ．abc ＞0，b 2－4ac ＜05．已知二次函数y ＝ax 2＋bx ＋c(a≠0)的图象如图所示，则下列结论中正确的是( ) A ．a ＞0B．c＜0C．3是方程ax2＋bx＋c＝0的一个根D．当x＜1时，y随x的增大而减小第5题图第6题图6．(2017·烟台中考)二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，对称轴是直线x ＝1，下列结论：①ab＜0；②b2＞4ac；③a＋b＋2c＜0；④3a＋c＜0.其中正确的是( ) A．①④B．②④C．①②③ D．①②③④7．(2017·营口一模)函数y＝x2＋bx＋c与y＝x的图象如图所示，有以下结论：①b2－4c＞0；②b＋c＋1＝0；③3b＋c＋6＝0；④当1＜x＜3时，x2＋(b－1)x＋c＜0.其中正确的是________(填序号)．8．二次函数y＝ax2＋bx＋c的图象如图所示，且P＝|2a＋b|＋|3b－2c|，Q＝|2a－b|－|3b＋2c|，比较P，Q的大小关系．参考答案与解析1．A2．C 解析：由y ＝ax 2＋bx ＋c 的图象开口向下，对称轴在y 轴右侧，得a ＜0，－b2a ＞0，∴b ＞0，∴反比例函数y ＝a x的图象位于第二、四象限，正比例函数y ＝bx 的图象位于第一、三象限．故选C.3．B 解析：由一次函数的图象可知k ＞1，∴－k ＜0，－1<－1k<0，∴抛物线开口向下，对称轴在直线x ＝－1与y 轴之间，与y 轴的交点在(0，1)的上方．故选B.4．B 5.C 6.C7．③④ 解析：∵二次函数y ＝x 2＋bx ＋c 与x 轴无交点，∴b 2－4ac ＜0，故①错误；当x ＝1时，y ＝1＋b ＋c ＝1，故②错误；∵当x ＝3时，y ＝9＋3b ＋c ＝3，∴3b ＋c ＋6＝0，故③正确；∵当1＜x ＜3时，二次函数值小于一次函数值，∴x 2＋bx ＋c ＜x ，∴x 2＋(b －1)x ＋c ＜0，故④正确．故正确的为③④.8．解：∵抛物线的开口向下，对称轴在y 轴右侧，∴a ＜0，－b2a＞0，∴b ＞0，∴2a－b ＜0.∵－b 2a ＝1，∴2a ＋b ＝0，a ＝－12b .当x ＝－1时，y ＝a －b ＋c ＜0，∴－12b －b ＋c＜0，∴3b －2c ＞0.∵抛物线与y 轴的正半轴相交，∴c ＞0，∴3b ＋2c ＞0，∴P ＝|2a ＋b |＋|3b －2c |＝3b －2c ，Q ＝|2a －b |－|3b ＋2c |＝b －2a －3b －2c ＝－2a －2b －2c ，∴Q －P ＝－2a －2b －2c －3b ＋2c ＝－2a －5b ＝－4b ＜0，∴P ＞Q .。

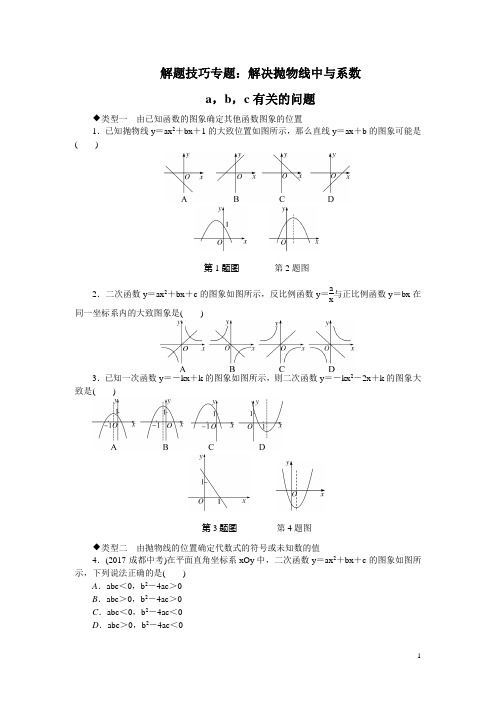
解题技巧专题：解决抛物线中与系数a，b，c有关的问题◆类型一由已知函数的图象确定其他函数图象的位置1．已知抛物线y＝ax2＋bx＋1的大致位置如图所示，那么直线y＝ax＋b的图象可能是()第1题图第2题图2．二次函数y＝ax2＋bx＋c的图象如图所示，反比例函数y＝ax与正比例函数y＝bx在同一坐标系内的大致图象是()3．已知一次函数y＝－kx＋k的图象如图所示，则二次函数y＝－kx2－2x＋k的图象大致是()第3题图第4题图◆类型二由抛物线的位置确定代数式的符号或未知数的值4．(2017·成都中考)在平面直角坐标系xOy中，二次函数y＝ax2＋bx＋c的图象如图所示，下列说法正确的是()A．abc＜0，b2－4ac＞0B．abc＞0，b2－4ac＞0C．abc＜0，b2－4ac＜0D．abc＞0，b2－4ac＜05．已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，则下列结论中正确的是() A．a＞0B．c＜0C．3是方程ax2＋bx＋c＝0的一个根D．当x＜1时，y随x的增大而减小第5题图第6题图6．(2017·烟台中考)二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，对称轴是直线x＝1，下列结论：①ab＜0；②b2＞4ac；③a＋b＋2c＜0；④3a＋c＜0.其中正确的是() A．①④B．②④C．①②③D．①②③④7．(2017·营口一模)函数y＝x2＋bx＋c与y＝x的图象如图所示，有以下结论：①b2－4c＞0；②b＋c＋1＝0；③3b＋c＋6＝0；④当1＜x＜3时，x2＋(b－1)x＋c＜0.其中正确的是________(填序号)．8．二次函数y＝ax2＋bx＋c的图象如图所示，且P＝|2a＋b|＋|3b－2c|，Q＝|2a－b|－|3b ＋2c|，比较P，Q的大小关系．参考答案与解析1．A2．C 解析：由y ＝ax 2＋bx ＋c 的图象开口向下，对称轴在y 轴右侧，得a ＜0，－b2a ＞0，∴b ＞0，∴反比例函数y ＝ax 的图象位于第二、四象限，正比例函数y ＝bx 的图象位于第一、三象限．故选C.3．B 解析：由一次函数的图象可知k ＞1，∴－k ＜0，－1<－1k <0，∴抛物线开口向下，对称轴在直线x ＝－1与y 轴之间，与y 轴的交点在(0，1)的上方．故选B.4．B 5.C 6.C7．③④ 解析：∵二次函数y ＝x 2＋bx ＋c 与x 轴无交点，∴b 2－4ac ＜0，故①错误；当x ＝1时，y ＝1＋b ＋c ＝1，故②错误；∵当x ＝3时，y ＝9＋3b ＋c ＝3，∴3b ＋c ＋6＝0，故③正确；∵当1＜x ＜3时，二次函数值小于一次函数值，∴x 2＋bx ＋c ＜x ，∴x 2＋(b －1)x ＋c ＜0，故④正确．故正确的为③④.8．解：∵抛物线的开口向下，对称轴在y 轴右侧，∴a ＜0，－b2a ＞0，∴b ＞0，∴2a－b ＜0.∵－b 2a ＝1，∴2a ＋b ＝0，a ＝－12b .当x ＝－1时，y ＝a －b ＋c ＜0，∴－12b －b ＋c ＜0，∴3b －2c ＞0.∵抛物线与y 轴的正半轴相交，∴c ＞0，∴3b ＋2c ＞0，∴P ＝|2a ＋b |＋|3b －2c |＝3b －2c ，Q ＝|2a －b |－|3b ＋2c |＝b －2a －3b －2c ＝－2a －2b －2c ，∴Q －P ＝－2a －2b －2c －3b ＋2c ＝－2a －5b ＝－4b ＜0，∴P ＞Q .。