立体几何中的组合体问题

关于球与多面体的组合体解题方法探讨球与多面体的组合体是三维几何中的一个重要概念，解题方法也有多种。

在此简要探讨一下关于球与多面体组合体的解题方法。

首先，对于球与多面体的组合体，我们可以将问题进行分解，分开考虑球和多面体的特性和性质，然后再综合起来考虑问题。

下面我们结合具体例题进行探讨。

例题1：一个正方体的棱长为2，一个半径为1的球被正方体完全包围住，且完全在正方体内，求球与正方体相交的面积。

解题思路：首先我们可以知道正方体的一个面上的对角线等于正方体的棱长，所以正方体的对角线长度为2√2由题目可知，球在正方体内，球的半径为1，则球心到正方体一些顶点的距离不会超过1，所以球心到正方体一些面的距离也不会超过1我们可以考虑球心到正方体各个面的距离，不难发现，球心到一个面的距离不超过1，球心到相对的面的距离不超过√2，球心到相对的对角面的距离不超过2综上所述，可以得到以下结论：1)若球心在正方体内部，则球与每一面都有交点；2)若球心在正方体边界上，即球心到一面的距离为1，则球与其对边的面无交点；3)若球心在正方体的角点上，即球心到对角面的距离为2，则球与对角面无交点。

在本题中，球心到正方体各个面的距离都不会超过1，所以球与每一面都有交点。

球与正方体的每一面的交线是一个圆，球与三个相邻的面的交线上的圆心在正方体的三个对角线的交点上，球与相对的两个面的交线上的圆心在每个对角面的对角线的交点上。

由于正方体是对称的，所以球与三个相邻的面的交线上的圆互相等价，同理，球与相对的两个面的交线上的圆互相等价。

因此，求球与正方体相交的面积，只需计算球与一个面的交线上的一个圆的面积即可。

球与面的交线上的圆的半径可以通过勾股定理得到，即球心到正方体其中一个面的距离。

在本题中，球心到正方体的一个面的距离为1，所以球与该面的交线上的圆的半径为1-1=0。

因此，球与该面的交线上的圆的面积为0。

综上所述，球与正方体相交的面积为0。

通过以上分析我们可以看出，在解这类球与多面体的组合体题目时，关键是找到球与多面体各个面的交线的性质和关系来进行求解。

1 / 4word.立体几何中的排列组合问题解法举隅立体几何中的排列组合问题在近年的高考数学试题中出现的频次较高，且常考常新. 因为解决这类问题不仅要具备排列组合的有关知识，而且还要具备较强的空间想象能力. 因而是一类既富思考情趣，又融众多知识和技巧于一体且综合性强、灵活性高、难度颇大的挑战性问题. 解决这类问题的关键是明确形成几何图形的元素，并与排列组合形成对应关系，转化为排列组合问题，同时还要注意避免重复和遗漏. 下面结合具体例子谈谈这类问题的求解方法，供参考. 一、分步求解例1 如果把两条异面直线看成“一对”，那么六棱锥的棱所在的12条直线中，异面直线有（ ）A. 12对B. 24对C. 36对D. 48对解 由于六棱锥的6条侧棱交于一点, 底面六边形的6条边共面, 因而只能将侧棱与底边相搭配. 第一步, 从6条侧棱中任取一条有16C 种; 第二步, 从底面6条边中与这条侧棱不相交的4条边中任取一条有14C 种, 由乘法原理知有1416C C =24对, 故选B.二．分类求解例2 四边形的一个顶点为A, 从其它顶点与各棱的中点中取3点, 使它们和点A 在同一平面上, 不同取法有( )A. 30种B. 33种C. 36种D. 39种解 符合条件的取法可分为两类: ①4个点(含A)在同一个侧面上,有30335C 种；②4个点（含A ）在侧棱与对棱中点的截面上，有3种. 由加法原理知不同取法共有33种，故选B.例3 将一个四棱锥的每个顶点染上一种颜色，并使同一条棱的两端异色，如果只有5种颜色可供使用，那么不同的染色方法种数是＿＿＿＿＿＿.2 / 4word.解 分三类：①如果用5种颜色有55A 种染色方法.②如果用4种颜色，只能是底面四边形相对顶点同色. 如图1，如果A 、C 同色，只要考虑染S 、A 、B 、D 四顶点，有45A 种染法，而B 、D 同色仍有45A 种染法，用四色共有245A 种染法.③如果用3种颜色，A 、C 同色，B 、D 同色，只要考虑S 、A 、B 三个顶点，有35A 种染法.由加法原理知共有55A ＋245A ＋35A ＝420种染法. 三、剔除求解例4 四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，则不同的取法共有（ ）A. 150种B.147种C.144种D.141种解 从10个点中任取4点，有410C 种取法，再剔除掉共面的取法.① 共面的四点在四面体的某一个面内，有46C 种取法，4个面共有446C 种；② 每条棱上的三个点与其对棱的中点四点共面，有6种；③由中位线构成的平行四边形（其两组对边分别平行于四面体相对的两条棱），它的4个顶点共面，有3种.故不共面的取法共有410C －446C －6－3＝141种，故选D.例5 已知正方体ABCD-A 1B 1C 1D 1. （1）以正方体顶点为顶点的四面体有多少个？（2）从8个顶点中取出3个顶点，使至少有两个顶点在同一棱上，其取法种数为多少？（3）过8个顶点中任两点的直线与直线A 1B 异面的有多少条？解 （1）从所有四点的组合中去掉共面的组合，6个表面四点共面，6个对角面四点共面. 所以共有四面体48C -12＝58个.图1BADCS图2ABC DB 1D 1C 1 A 13 / 4word.（2）如图2， A 1BD 这样的三点不能满足题意，可以认为这个三点组合与顶点A 对应，正方体有8个顶点，每个顶点对应一个不合题意的三点组合. 所以满足题意的三点取法共有38C －8＝48种.（3）在8个顶点取2个的组合中，去掉侧面ABB 1A 1中的两点组合有24C 个，再去掉过A 1不在面ABB 1A 1内的四条直线与过B 的4条直线，还要去掉与之平行的D 1C.所以共有1442428----C C ＝13条. 四、构造模型求解例6 与空间不共面的四点距离相等的平面有多少个？解 由题设条件，空间不共面的四点可构成四面体，考虑四面体的四个顶点在所求平面两侧的分布，易知当所求平面位于三棱锥的顶点与底面之间时有4个；当所求平面位于三棱锥相对棱之间时有3个. 故所求平面有7个. 例7 在正方体八个顶点的所有连线中，有多少对异面直线？解 构造四面体求解，因为四面体的6条棱可构成3对异面直线，从而只要求出正方体的八个顶点可构成几个四面体即可，而这恰好是本文例5（1），故可得到1743)12(48=⨯-C 对异面直线.五、联想有关命题求解例8 以长方体的八个顶点中的任意3个为顶点的所有三角形中，锐角三角形的个数为（ ）A.0B.6C.8D.24解 联想课本习题：“将正方体截去一角，求证：截面是锐角三角形. ”易知从长方体的一个顶点出发的三条棱的另3个端点可构成锐角三角形，长方体有8个顶点，从而可构成8个锐角三角形，故选C.六、综合有关知识求解例9 以一个正五棱柱的顶点为顶点的四面体共有（ ） A.200个 B.190个 C.185个 D.180个图3CE C 14 / 4word.解 正五棱柱共有10个顶点，若每四个顶点构成一个四面体，共可构成410C ＝210个四面体，其中四点在同一平面内的有三类： ① 每一底面的5点中选4点的组合方法有452C 个. ② 5条侧棱中的任意两条棱上的四点有25C 个.③一个底面的一边与另一个底面相应的一条对角线平行（例如AB ∥E 1C 1），这样共面的四点共有152C 个.故四面体的个数为15254541022C C C C ---＝180个，故选D.例10 用正五棱柱的10个顶点中的5个顶点作四棱锥的5个顶点，共可得多少个四棱锥？解 结合图3，以不同类型的四棱锥的底面分类可得：① 以棱柱的底面为四棱锥底面的共有245C 15C 个. ②以棱柱的侧面为四棱锥底面的共有15C 16C 个. ③以棱柱的对角面为四棱锥底面的共有15C 16C 个.④以图3中ABC 1E 1（为等腰梯形）为四棱锥底面的共有215C 16C 个. 故可构成的四棱锥共有245C 15C ＋15C 16C ＋15C 16C ＋215C 16C ＝170个.例11 以四棱柱的顶点为顶点的三棱锥有多少个？解 本题要讨论底面的形状，所求的答案与底面的形状有关. ①若底面不是梯形，也不是平行四边形，则有48C －6－2＝62个. ② 若底面是梯形，则有48C －6－4＝60个. ③ 若底面是平行四边形，则有48C －6－6＝58个. 综上所述，所求三棱锥的个数为62或60或58.最新文件---------------- 仅供参考--------------------已改成word 文本 --------------------- 方便更改。

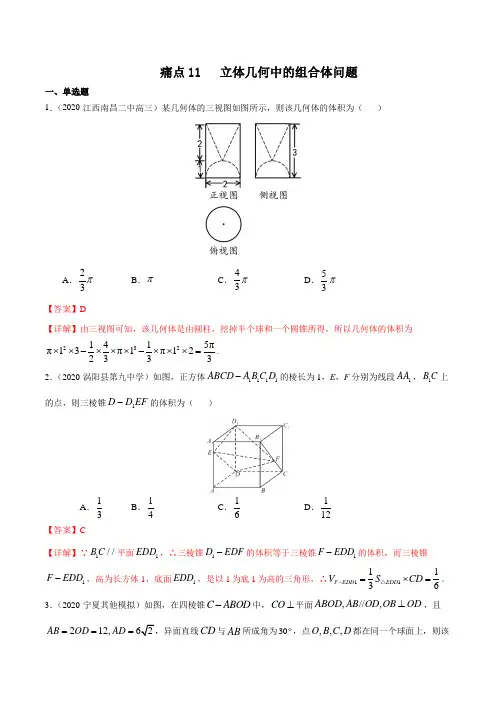
痛点11 立体几何中的组合体问题一、单选题1．（2020·江西南昌二中高三）某几何体的三视图如图所示，则该几何体的体积为（ ）A ．23π B ．πC ．43π D ．53π 【答案】D【详解】由三视图可知，该几何体是由圆柱，挖掉半个球和一个圆锥所得，所以几何体的体积为2321415ππ13π1π122333⨯⨯-⨯⨯⨯-⨯⨯⨯=. 2．（2020·涡阳县第九中学）如图，正方体1111ABCD A B C D -的棱长为1，E ，F 分别为线段1AA ，1B C 上的点，则三棱锥1D D EF -的体积为（ ）A ．13B ．14C ．16D ．112【答案】C【详解】∵1//B C 平面1EDD ，∴三棱锥1D EDF -的体积等于三棱锥1F EDD -的体积，而三棱锥1F EDD -，高为长方体1，底面1EDD ，是以1为底1为高的三角形，∴111613△-==⨯F EDD EDD V S CD 。

3．（2020·宁夏其他模拟）如图，在四棱锥C ABOD -中，CO ⊥平面,//,ABOD AB OD OB OD ⊥，且212,2AB OD AD ===异面直线CD 与AB 所成角为30，点,,,O B C D 都在同一个球面上，则该球的半径为 （ ）A ．32 B．42 C ．21 D．42【答案】C【解析】由条件可知AB OD ∥ ，所以，CDO ∠ 为异面直线CD 与AB 所成角，故30CDO ∠= ，而6OD =，故tan 3023OC OD =⋅= ，在直角梯形ABOD 中，易得6OB = ，以,,OB OC OD 为相邻的三条棱，补成一个长方体，则该长方体的外接球半径R 即为所求的球的半径，由()()22222236684R =++= ，故21R = .4．（2020·全国高三月考）一个几何体的三视图如图所示，已知其体积为483π+，则图中r 的值为( )A ．1B ．2C ．3D ．4【答案】B 【详解】由三视图可知，该几何体由两个相同圆锥的14与一个三棱柱组成，所以该几何体体积22331114228243263V r r r r r r r πππ=⨯⨯⨯+⨯=+=+⇒=.5．6的半球切削成一个正方体（保持正方体的一个面在半球底面所在平面上），所得正方体体积的最大值为（ ）A ．42B ．8C ．22D ．4【答案】B【详解】由题意：当正方体内接于半球时体积最大，如图，连接球心O 与点C ，连接1OC ，则16OC =．设正方体棱长为a ，则在1Rt OCC ∆中，22211OC CC OC +=，22262a a ⎛⎫+= ⎪ ⎪⎝⎭，解得2a =，故正方体体积的最大值为8． 6．（2020安徽高三）已知某几何体的三视图是如图所示的三个直角三角形，则该几何体的外接球的表面积为（ ）A ．17πB ．34πC ．51πD ．68π【答案】B【详解】由三视图知原几何体是三棱锥A BCD -，如图，AB ⊥平面BCD ，CD ⊥平面ABD ．由这两个线面垂直，得,AB BC AD CD ⊥⊥，因此AC 的中点O 到,,,A B C D 四顶点的距离相等，即为外接球球心． 由三视图得22345+=AD ，22225334AC AD CD =++，∴24()342AC S ππ=⨯=．7．现有一副斜边长相等的直角三角板.若将它们的斜边AB 重合，其中一个三角板沿斜边折起形成三棱锥A BCD -，如图所示，已知,64DAB BAC ππ∠=∠=，三棱锥的外接球的表面积为4π，该三棱锥的体积的最大值为（ ）A ．33B 3C ．324D ．348【答案】B【详解】设三棱锥A BCD -的外接球的半径为r ，因为244r ππ=⇒1r =，因为90ADB ACB ︒∠=∠=，所以AB 为外接球的直径，所以2AB =，且3,1,2AD BD AC BC ====当点C 到平面ABD 距离最大时，三枝锥A BCD -的体积最大，此时平面ABC ⊥平面ABD ，且点C 到平面ABD 的距离1d =，所以11133113326A BCD C ABD ABD V V S d --==⋅=⨯⨯=△. 8．（2020·沙坪坝·重庆一中）阿基米德（公元前287年—公元前212年），伟大的古希腊哲学家、数学家和物理学家，他死后的墓碑上刻着一个“圆柱容球”的立体几何图形，为纪念他发现“圆柱内切球的体积是圆柱体积的23，且球的表面积也是圆柱表面积的23”这一完美的结论.已知某圆柱的轴截面为正方形，其表面积为24π，则该圆柱的内切球体积为( )A ．43π B ．16πC ．163π D ．323π 【答案】D【详解】设圆柱的底面半径为r ,则其母线长为2l r =,因为圆柱的表面积公式为2=22S r rl ππ+圆柱表，所以222224r r r πππ+⨯=,解得2r,因为圆柱的体积公式为2=2V Sh r r π=⋅圆柱,所以3=22=16V ππ⨯⨯圆柱,由题知,圆柱内切球的体积是圆柱体积的23，所以所求圆柱内切球的体积为2232=16=333V V ππ=⨯圆柱. 9．（2020·陕西高三）已知正四面体的内切球体积为v ，外接球的体积为V ，则Vv=（ ）A ．4B ．8C ．9D ．27【答案】D【详解】设正四面体的棱长为1，取BC 的中点为D ，连接AD ，作正四面体的高为PM ，则323,233AD AM AD ===，2263PM PA AM ∴=-=，136234312P ABC V -∴=⨯⨯=， 设内切球的半径为r ，内切球的球心为O ，则134434P ABC O ABC V V r --==⨯⨯，解得：612r =；设外接球的半径为R ，外接球的球心为N ，则MN PM R =-或R PM -，AN R =，在Rt AMN ∆中，由勾股定理得222AM MN AN +=，22163R R ⎫∴+-=⎪⎪⎝⎭，解得64R =，3R r ∴=，3327V R v r ∴==。

立体几何与球体组合计算方法立体几何是研究物体在三维空间中的形状、大小和相互关系的数学分支。

而球体是一种特殊的立体几何图形，具有球心、半径和表面等特征。

在实际生活和工程应用中，我们常常需要计算球体与其他几何形体的组合问题，比如球与立方体、球与圆柱体等。

本文将介绍一些常见的立体几何与球体组合计算方法。

一、球与立方体组合计算方法1. 球心在立方体内部当球心位于立方体内部时，我们需要计算球体与立方体的重叠部分体积。

首先，求出球体与立方体的交点，即求出球体的截面。

根据截面的形状，可以使用不同的方法进行求解。

其中一种常见的方法是使用球的方程和立方体的坐标方程求解截面的交点坐标。

然后，计算截面内的体积，最后将各个截面的体积相加即可得到球体与立方体组合的体积。

2. 球心在立方体外部当球心位于立方体外部时，我们需要计算球体与立方体的相交部分体积。

同样地，首先求解球体与立方体的交点坐标。

然后，计算球体在立方体内的投影体积，即球体在立方体内的部分。

最后，将投影体积与球体与立方体相交部分的体积相加即可得到球体与立方体组合的体积。

二、球与圆柱体组合计算方法1. 球心在圆柱体内部当球心位于圆柱体内部时，我们需要计算球体与圆柱体的相交部分体积。

类似于球与立方体的组合，首先求解球体和圆柱体的交点坐标。

然后，根据截面的形状使用相应的方法计算截面的体积。

最后，将各个截面的体积相加即可得到球体与圆柱体组合的体积。

2. 球心在圆柱体外部当球心位于圆柱体外部时，我们需要计算球体与圆柱体的相交部分体积。

同样地，首先求解球体与圆柱体的交点坐标。

然后，计算球体在圆柱体内的投影体积。

最后，将投影体积与球体与圆柱体相交部分的体积相加即可得到球体与圆柱体组合的体积。

三、其他球体组合计算方法除了与立方体和圆柱体的组合，球体还可以与其他几何形体进行组合。

例如，球体与锥体的组合，球体与棱台的组合等。

对于这些组合，我们同样可以采用类似的方法进行计算。

首先求解交点坐标，然后计算截面的体积，最后将各个截面的体积相加即可得到组合的体积。

行测立体组合体诀窍行测考试中的立体组合体题目主要涉及到计算立方体、长方体、棱柱、棱锥、圆柱、圆锥等多种几何图形的体积、表面积、相交关系等问题。

以下是解决此类题目的几个窍门：1. 熟记几何公式：- 立方体的体积公式：V = a^3，表面积公式：S = 6a^2- 长方体的体积公式：V = lwh，表面积公式：S = 2lw + 2lh + 2wh- 棱柱的体积公式：V = Bh，其中B为底面积，h为高，表面积公式：S = B + 2Ph，其中P为底面周长- 圆柱的体积公式：V = πr^2h，表面积公式：S = 2πr(r + h)- 棱锥的体积公式：V = 1/3Bh，其中B为底面积，h为高，表面积公式：S = B + 1/2Pl，其中P为底面周长，l为斜高- 圆锥的体积公式：V = 1/3πr^2h，表面积公式：S = πr(r + l)，其中l为斜高2. 观察立体图形的特点：- 理解立体图形的特点，比如长方体的六个面都是矩形，棱柱的侧面是矩形，底面是多边形等。

- 通过观察，确定需要计算的量和已知量，使用对应的公式求解。

- 注意边长、高、斜高等概念的理解和运用，合理选择适合的公式进行计算。

3. 切割与组装法：- 针对复杂立体图形，可以通过切割与组装简单立体图形的方法进行计算。

- 将复杂图形切割为几个简单的立体图形，然后通过计算各个简单图形的体积、表面积等，最后进行加减运算得到复杂立体的结果。

- 注意切割时要维持图形的完整性，避免几何图形的盖、底未能完全平行，或者缺失引起计算错误。

4. 绘制示意图：- 绘制示意图有助于理解和分析立体图形的结构，可以更清晰地确定计算关系。

- 在解题过程中，尽量用简单、明了的示意图代替文字描述，尤其是在涉及图形相交、分割等复杂情况下，有助于清晰把握题意，防止出错。

5. 多积累题目：- 多做一些立体组合体的相关练习题，积累解题经验和技巧。

- 题目中涉及到的具体数据和计算方法可能会有所不同，通过多做题，熟悉题目类型和题目解法，能更好地应对考试中的各种情况。

例析立体几何中的排列组合问题过月圆春晖中学在数学中，排列、组合无论从内容上还是从思想方法上，都体现了实际应用的观点。

立体几何与排列组合综合问题是高考命题的新趋势，体现了《考试大纲》要求的在知识交汇处命题的指导思想，应引起考生的重视。

立体几何中的计数问题也是高考的热点题型，解决这类问题的基本方法是以点带面法，下面列举立体几何中排列、组合问题的几个例子。

1 点1．1 共面的点11997年全国高考（文））（例A3A在同四面体的一个顶点为个点，使它们和点，从其它顶点与棱的中点中取）一平面上，不同的取法有（A30 B33 C36 D39种种．种．．．种4666A所解析：四面体有个中点，每个面上的个顶点，个点共面。

点条棱有34AA个面内，共有在点组合有个，点在的每个面中含个组合；点的A6333点与这条棱对棱的中点共面。

条棱的个点，这条棱上，每条棱上有在A共面的四点组合共有个。

所以与点B答案：97文科试题中难度最大的选点评：此题主要考查组合的知识和空间相像能力；属3点与它对棱上的中点共面的情况计择题，失误的主要原因是没有把每条棱上的算在内。

1．2 不共面的点21997年全国高考（理））（例104个不共面的点，不同的取法共有个点，在其中取四面体的顶点和各棱中点共）（A150 B147 C144 D141种．种．种．种．410 4点共面的情况有三类：第一个点中任取个点有解析：从种取法，其中4个点位于四面体的同一个面内，有种；第二类，取任一条棱上类，取出的346种；第三类，由中位线构成的平行四边的个点及对棱的中点，这点共面有43种。

形，它的个顶点共面，有以上三类情况不合要求应减掉，所以不同取法共有种。

D答案：。

点评：此题难度很大，是当时高考中得分最低的选择题，对空间想像能力要求高，很好的考察了立体几何中点共面的几种情况；排列、组合中正难则反易的解题技巧及分类讨论的数学思想。

2 直线例3（2005年全国高考卷Ⅰ（理））过三棱柱任意两个顶点的直线共15条，其中异面直线有（）A．18对B．24对C．30对D．36对分析：选项数目不大，若不宜用公式直接求解，可考虑用树图法。

立体几何中组合问题的几种解法解决几何组合问题时，应准确灵活使用加法原理和乘法原理，要分类分步进行，做到不重复不遗漏。

1 直接求解法例1：四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，不同的取法有多少种?分析：正面考虑本题各步骤的方法比较复杂，计算困难，应运用逆向思维，即先考虑从10个点任意取出4个点的方法，再减去从10个点中取出4点共面的的方法即可。

解：从10个点中找出4个点的方法有Ｃ410=210种，其中在四面体的四个面内各有6个点，取出共面的4个点的方法有4Ｃ4■=60种；相邻面各棱的中点4点共Ｃ410面的有3种；一条棱上三点与其相对棱中点也共面，共6种。

∴所求方法N=210-60-3-6=141(种)本题应注意“哪些点共面?”共有几种情况?[1]例2：从平面Ⅱ上取6个点，再从平面B上取4个点，这10个点最多可确定多少个三棱锥?解法①：分三种情况考虑：第一种情况从平面a上的6个点中任取一个再与从平面β上的4个点中任取3个点构成的三棱锥有Ｃ1■Ｃ■■个；第二种情况，从平面a上的6个点中任取2个与平面13上的4个点中任取2个点构成的三棱锥有Ｃ2■Ｃ2■个；第三种情况，从平面a上的6个点中任取3个点与平面β上的4个点中任取1个点构成的三棱锥有Ｃ■■Ｃ1■个。

根据加法原理共有Ｃ1■Ｃ■■+Ｃ2■Ｃ2■ +Ｃ■■Ｃ1■ =24+90+80=194(个)。

解法②：逆向思维：从10个点中任取4个点的组合数Ｃ410中，去掉4个点共面的两种情况即4点在平面a上的Ｃ4■个，4点在平面β上的Ｃ4■个。

其余的任4点都能构成一个三棱锥。

因此，可构成三棱锥Ｃ410-Ｃ4■-Ｃ4■=210-15-1=194(个)。

2 从几何概念上求解［2］例3：空间10个点，无三点共线，其中有六个点共面，其余无四个点共面，则这些可以组成四棱锥的个数有多少个?此题易错解，仿上例。

错解一：从共面的6个点中任取1个、2个、3个、4个点，与从另外4个不共面的点中任取4个、3个、2个、1个点可构成的四棱锥有Ｃ1■Ｃ4■＋Ｃ2■Ｃ■■＋Ｃ■■Ｃ2■=6+60=120+60=246(个)。

例谈立体几何中的排列组合概率问题张世林 谭升平在近几年的高考试题中，出现了以立体几何中的点、线、面的位置关系为背景的排列、组合、概率问题。

这类问题情景新颖，多个知识点交汇在一起，综合性强，往往作为高考选择填空题的压轴题。

它不仅考查了相关的基础知识，而且还注重对数学思想方法及数学能力的考查。

一、共面问题：分类讨论例1. 不共面的四个定点到平面α的距离都相等，这样的平面α共有（ ）A. 3个B. 4个C. 6个D. 7个解析：平面α可以分为两类：一类是在平面α的两侧各有两个点；另一类是在平面α的两侧分别有一个点和三个点。

如图1，设E、F、G、H、M分别是AB、AC、AD、CD、BD的中点，过E、F、G三点的平面α满足题意，这样的平面有4个；又过E、F、H、M的平面α也满足题意，这样的平面有3个。

故适合题设的平面α共有7个，应选D。

图1例2. 在四棱锥P�ABCD中，顶点为P，从其他的顶点和各棱的中点中取3个，使它们和点P在同一平面上，不同的取法有（）种。

A. 40B. 48C. 56D. 62图2解析：如图2，满足题设的取法可分为三类：（1）在四棱锥的每个侧面上除点P外任取3点，有（种）不同的取法； （2）在两个对角面上除点P外任取3点，共有（种）不同的取法；（3）过点P的每一条棱上的三点和与这条棱异面的棱的中点也共面，共有（种）不同的取法。

故不同的取法共有（种）。

点评：这类问题应根据立体图形的几何特点，选取恰当的分类标准，做到分类既不重复，也不遗漏。

在例2中，最容易漏掉的是第（3）类，最易重复的也是第（3）类。

二、异面问题：灵活转化例3. 过三棱柱任意两个顶点的直线共15条，其中异面直线有（ ）A. 18对B. 24对C. 30对D. 36对解析：大家知道一个三棱锥可以确定3对异面直线，一个三棱柱可以组成（个）三棱锥，则共有36对异面直线。

故选D。

点评：利用熟知的立体图形来灵活转化，是处理异面直线配对问题的常用方法。