数学七年级下册周周清-第一周

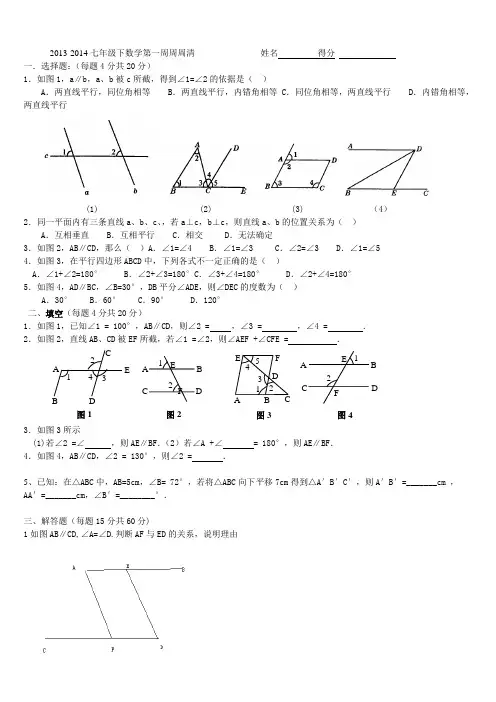
2013-2014七年级下数学第一周周周清姓名得分一．选择题：（每题4分共20分）1．如图1，a∥b，a、b被c所截，得到∠1=∠2的依据是（）A．两直线平行，同位角相等 B．两直线平行，内错角相等 C．同位角相等，两直线平行 D．内错角相等，两直线平行(1) (2) (3) （4）2．同一平面内有三条直线a、b、c、，若a⊥c，b⊥c，则直线a、b的位置关系为（）A．互相垂直 B．互相平行 C．相交 D．无法确定3．如图2，AB∥CD，那么（）A．∠1=∠4 B．∠1=∠3 C．∠2=∠3 D．∠1=∠54．如图3，在平行四边形ABCD中，下列各式不一定正确的是（）A．∠1+∠2=180° B．∠2+∠3=180°C．∠3+∠4=180° D．∠2+∠4=180°5．如图4，AD∥BC，∠B=30°，DB平分∠ADE，则∠DEC的度数为（）A．30° B．60° C．90° D．120°二、填空（每题4分共20分）1．如图1，已知∠1 = 100°，AB∥CD，则∠2 =，∠3 =，∠4 =．2．如图2，直线AB、CD被EF所截，若∠1 =∠2，则∠AEF +∠CFE =．3．如图3所示(1)若∠2 =∠，则A E∥BF．（2）若∠A +∠= 180°，则AE∥BF．4．如图4，AB∥CD，∠2 = 130°，则∠2 =．5、已知：在△ABC中，AB=5cm，∠B= 72°，若将△ABC向下平移7cm得到△A′B′C′，则A′B′=_______cm ，AA′=_______cm，∠B′=________°．三、解答题（每题15分共60分)1如图AB∥CD,∠A=∠D.判断AF与ED的关系，说明理由图124 31ABCDE12A BDCEF图21 2345A B CDFE图312A BC DEF图42、如图，∠1与∠2互为补角，∠3=1170，求∠4的度数．(6分)2．如图，∠1=130°，∠D =50°．AB 与DE 平行吗？为什么？（用至少2种方法）3、将下列方格纸中的△ABC 向右平移10格，再向上平移2格，得到△111C B A ． （1）画出平移后的三角形；（2）若BC=3cm ，则11C A = cm ．（3）如果AC ⊥BC ，则∠C 1= °．AC B 1F A B DE C。

七年级下学期第一周数学周周清一、单选题1．下列运算中，正确的是（）A．B．C．D．2．若,则下面多项式不成立的是( )A．B．C．D．3．计算（－2）2009+（－2）2010的结果是（）A．22019B．22009C．－2 D．－22010 4．若102a=x,10b=y，则104a＋2b的值为( )A．xy B．x2yC．x2y2D．xy25．若，那么的值是( )A．10 B．52 C．20 D．32 6．若26＝a2＝4b，则a b等于( )A．43B．82C．83D．48 7．下列各式与x3n＋2相等的是( )A．(x3)n＋2B．(x n＋2)3C．x2·(x3)n D．x3·x n＋x2 8．若3x＋4y－5＝0，则8x·16y的值是( )A．64 B．8 C．16 D．32 9．已知，，则等于（）A．B．C．17 D．7210．已知a m=9，a m﹣n=3，则a n的值是（）A．﹣3 B．3 C．D．111．计算：(-3b3)2÷b2的结果是( )A．-9b4B．6b4C．9b3D．9b4 12．x5-n 可以写成（）A．x5÷x n B．x5 +x n C．x+x n D．5x n二、填空题13．计算：（－）2017×（1）2018＝___________.14．(1)若2m=3,2n=5，则4m＋n=____；(2)若3x=4,9y=7，则3x－2y的值为____.15．（）计算：__________．（）计算：__________．16．若，则的值是_______.17．已知，，m，n是正整数，则用a，b的式子表示=_________．18．若，则n= _____．三、解答题19．如果，求的值．20．（）已知，，求的值．（）已知，求的值．21．（）如果，求的值．（）已知，求的值．22．已知a n=-1,b2n=3,求(-a2b)4n的值.23．若，，求的值。

七年级数学（下）周周清试卷（一）命题人：宿丑云班级 姓名 成绩 .一、填空：（每空2分，共32分） 1． 1、如右图所示，根据所给条件填空： （1）∵∴a ∥b （同位角相等，两直线平行） （2）∵∴a ∥b （内错角相等，两直线平行） （3）∵∴a ∥b （同旁内角互补，两直线平行） 2． 如右图，若a ∥b ，则可以得到：（1）、 （ ） （2）、 （ ） （3）、 （ ） 3、如右图，已知 ， ，则 =_________.4、如图，已知，，则.第4题 第5题5、如图，已知 ， ，则 .6、如右图，若已知∠D ＋∠C ＝180°，可以判定_____和______平行；若∠1＝∠2，可以判定______和______平行. 二、选择题（每题3分，共36分）：1、下列说法正确的是（ ）.A ．经过一点有一条直线与某一直线平行B ．过一点有无数条直线与已知直线平行C ．过一点有且只有一条直线与已知直线平行D ．过直线外一点有且只有一条直线与已知直线平行ab c12342、下列表示方法正确的是（）.A．B．C．D．3、下面推理正确的是（）.A．B．C．D．4、如下图，直线和被所截，下面说法正确的是（）.A．因为∠1和∠2互补，所以直线B．当∠2=∠3时，C．如果∠1＝∠2，则D．如果∠1＝∠3，则5、如右图，已知∠1＝80°，a//b，则∠2的度数为（）.A．100°B．70°C．80° D．60°6、如右图，已知∠1＝100°，∠2＝80°，∠3＝50°，∠4＝130°，则a与c的关系是（）.A．相交 B．平行C．垂直 D．不确定7、如下图，AB//CD，若∠2是∠1的2倍，则∠2等于（）.A．60° B．90°C．120° D．150°8、下列推理中，错误的是（）．A．B．C．D．9、如右图，由A测B的方向是（）A．南偏东30°B．南偏东60°C．北偏西30°D．北偏西60°10、如图， ， ， ，则的度数是（ ）A ．60°B ．70°C ．80°D ．65°11、若两条平行线被第三条直线所截，则一组同位角的平分线互相（ ）. A ．垂直 B ．平行 C ．重合 D ．相交 12、已知直线AB//CD ，EF 与AB 、CD 相交于点E 、F ，如右图，若∠1＝120°则∠2的度数是（ ）.A ．15°B ．30°C ．60°D ．120° 三、解答题1、（本题6分）如图，已知，. 试说明.证明：∵（已知），∴ （ ）. ∵ （已知），∴ （等量代换）.∴（ ）.2、（本题4分）如图， ，.试说明：AB∥CD.3、（本题6分）如图，AE 、CE 分别平分 和，若 和 互余.求证：AB∥CD.证明：∵AE 、CE 分别平分 、 （已知），∴ （ ）. ∴.12A BC D EF Gabcd123∵ 和 互余（已知），∴∠1+∠2＝ °（互余的定义）. ∴.∴ （ ）. 4、（本题6分）依据下列语句画图（1） 点P 是直线AB 外一点，直线CD 经过点P ，且与直线AB 平行.（2）如图，过E 作线段EF∥AC 交AB 于F 。

七年级数学学科周周清（1）
姓名：等级：
1
球正方体圆柱圆锥长方体
像长方体、正方体、圆柱、圆锥、球等都是（）简称为体
2观察上面几何体的表面特点将它们分类：（）（）和（）
为一类因为它们的面有的为曲面.（）和（）的面都是平的为
一类，像这一类几何体也叫多面体.
3 长方体有_________个面,共有___条棱.
4 三棱柱有5个面,6个顶点,9条棱;四棱柱有6个面,8个顶点,12条棱;五棱柱有( )面,( )个顶点,( )条棱。

5马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如图所示的拼接图形（实线部分），经折叠后发现还少
一个面，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子．（注：①只需添加一个符合要求的正方形；②添加的正方形用阴影表
示）
6观察下列多面体，并把下表补充完整．观察上表中的结果，你能发现a、b、c之间有什么关系吗？请写出关系式．
水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示．如图，是一个正方体的平面展开图，若图中“锦”为前面，“似”为下面，“前”为后面，则“祝”表示正方体的那个面？
7美丽的图形由有基本的图形组合而成，请你在下面网格中设。

周周清（1）姓名学号得分一．选择题（共12小题，每题3分，共36分）一．选择题（共12小题，共36分）1．如图，检测4个足球的质量，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数，从质量角度看，最接近标准的是（）A．B．C．D．2．下列各数：﹣，﹣0.7，﹣9，25，π，0，﹣7.3中，分数有（）个．A．1B．2C．3D．43．﹣2019的绝对值的相反数是（）A．﹣2019B．2019C．D．4．在下列气温的变化中，能够反映温度上升5℃的是（）A．气温由﹣5℃到5℃B．气温由﹣1℃到﹣6℃C．气温由5℃到0℃D．气温由﹣2℃到3℃5．下列说法正确的是（）A．一个数的绝对值等于它本身，这个数一定是正数B．一个数的绝对值等于它的相反数，这个数一定是负数C．绝对值越大，这个数越大D．两个负数，绝对值大的那个数反而小6．下列各式错误的是（）A．﹣（﹣3）＝3 B．|2|＝|﹣2| C．0＞|﹣1| D．﹣2＞﹣37．绝对值大于3且小于6的所有整数的和是（）A．0B．9C．18D．278．﹣a一定是（）A．正数B．负数C．0D．不确定9．已知a是最大的负整数，b是绝对值最小的数，c是最小的正整数，则a+b+c等于（）A．2B．﹣2C．0D．﹣610．如图，点A表示的有理数是x，则x，﹣x，1的大小顺序为（）A．x＜﹣x＜1B．﹣x＜x＜1C．x＜1＜﹣x D．1＜﹣x＜x11．已知|a |＝1，b 是2的相反数，则a +b 的值为（ ） A ．﹣3B ．﹣1C ．﹣1或﹣3D ．1或﹣312．如图，圆的周长为4个单位长度．在该圆的4等分点处分别标上数字0、1、2、3，先让圆周上表示数字0的点与数轴上表示数﹣1的点重合，再将数轴按逆时针方向环绕在该圆上．则数轴上表示数﹣2019的点与圆周上表示数字（ ）的点重合． A ．0B ．1C ．2D ．3二．填空题（共6小题，共18分）13.的倒数是 ，相反数是 ，绝对值是14.用“＞”、 “＜”、“=”号填空：5465--，⎪⎭⎫ ⎝⎛----32732715．数学考试成绩以80分为标准，王老师将某4名同学的成绩简记为+10，0，﹣8，+18，则这4名同学实际成绩最高的是 分．16．如图，数轴上有O 、A 、B 三点，点O 对应原点，点A 对应的数为﹣1，若OB ＝3OA ，则点B 对应的数为 ． 17．若|3x ﹣2|与|y ﹣1|互为相反数，则xy ＝ ． 18．如果x 、y 都是不为0的有理数，则代数式的值是 ．三．解答题（共9小题） 19．（20分）计算：(1)(2)(5)-+- (2)(26)(6)(44)(104)-+++-++31321(3)(2)2(7)(2)(8)52452-++++-+- (4)( 5.6)0.9( 4.4)(8.1)(1)-++-++++20．（8分）（1）将下列各数填入相应的圈内：4，﹣3，0，1.5，+2，﹣5．（2）说出这两个圈的重叠部分表示的是什么数的集合．（3）在如图所示的数轴上表示出这些数，并用“＞”把它们连接起来21．（8分）若|a|＝4，|b|＜2，且b为整数．（1）求a，b的值；（2）当a，b为何值时，a+b有最大值？并求出a+b的最大值？22．（8分）王先生到市行政中心大楼办事，假定乘电梯向上一楼记作+1，向下一楼记作﹣1，王先生从1楼出发，电梯上下楼层依次记录如下（单位：层）：+6，﹣3，+10，﹣8，+12，﹣7，﹣10．（1）请你通过计算说明王先生最后是否回到出发点1楼．（2）该中心大楼每层高3m，电梯每向上或下1m需要耗电0.2度，根据王先生现在所处位置，请你算算，他办事时电梯需要耗电多少度？23．（10分）结合数轴与绝对值的知识回答下列问题：（1）数轴上表示4和1的两点之间的距离是；表示﹣3和2两点之间的距离是；一般地，数轴上表示数m和数n的两点之间的距离等于|m﹣n|．如果表示数a和﹣1的两点之间的距离是3，那么a＝．（2）若数轴上表示数a的点位于﹣4与2之间，则|a+4|+|a﹣2|的值为；（3）利用数轴找出所有符合条件的整数点x，使得|x+2|+|x﹣5|＝7，这些点表示的数的和是．24.（12分）A、B、C三点则数轴上，点A表示的数是-6，点B则原点的右边且与点A相距15个单位长度. （1）求出B点表示的数，画一条数轴并则数轴上标出点A和点B；（2）若此数轴则一张纸上，将纸沿某一条直线对折，此时B点与表示-1的点刚好重合，折痕与数轴有一个交点D，求点D表示的数的相反数；（3）A、B从初始位置分别以1单位长度每秒和2单位长度每秒同时向左运动，是否存在t的值，使得t 秒后点B到原点的距离与点A到原点的距离相等？若存在，请求出t的值；若不存在，请说明理由.A，B，C的距离和为40个单位？。

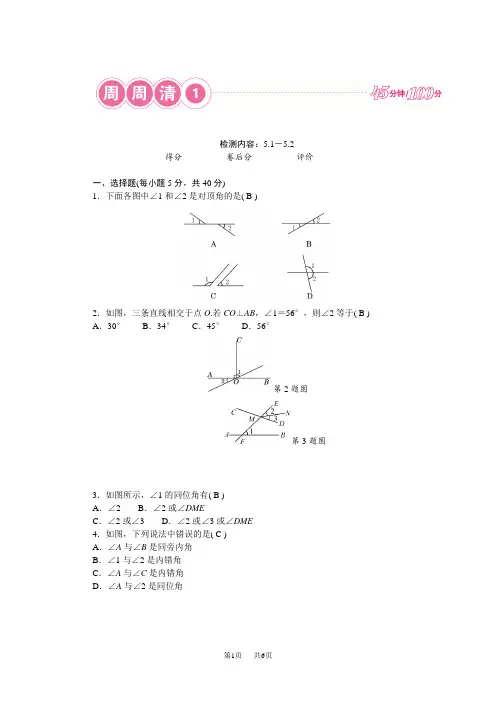
检测内容：5.1－5.2得分________卷后分________评价________一、选择题(每小题5分，共40分)1．下面各图中∠1和∠2是对顶角的是( B )2．如图，三条直线相交于点O.若CO⊥AB，∠1＝56°，则∠2等于( B ) A．30°B．34°C．45°D．56°第2题图第3题图3．如图所示，∠1的同位角有( B )A．∠2 B．∠2或∠DMEC．∠2或∠3 D．∠2或∠3或∠DME4．如图，下列说法中错误的是( C )A．∠A与∠B是同旁内角B．∠1与∠2是内错角C．∠A与∠C是内错角D．∠A与∠2是同位角第4题图第5题图5．如图所示，∠BAC＝90°，AD⊥BC，垂足为D，则下列结论：①AB与AC互相垂直；②AD与AC互相垂直；③点C到AB的垂线段是线段AB；④线段AB的长度是点B到AC的距离．其中正确的个数有( B )A.1个B．2个C．3个D．4个6．如图，三条直线AB，CD，EF相交于点O，若∠1＝2∠2，∠3比∠1大30°，则∠4的度数为( B )A．65°B．60°C．50°D．45°第6题图第7题图7．如图，直线l1，l2被直线l3，l4所截，下列条件中，不能判断直线l1∥l2的是( B ) A．∠1＝∠3 B．∠5＝∠4C．∠5＋∠3＝180°D．∠4＋∠2＝180°8．如图，AB∥CD的条件是( D )A.∠B＝∠DB．∠B＋∠D＝90°C．∠B＋∠D＋∠E＝180°D．∠B＋∠D＝∠E二、填空题(每小题5分，共10分)9．如图，直线AB，CD，EF交于一点O，OG⊥EF，且∠GOB＝30°，∠AOC＝40°，则∠COE＝__20°__.第9题图第10题图10．如图，(1)如果∠1＝__∠C__，那么DE∥AC；(2)如果∠1＝__∠DEF__，那么EF∥BC；(3)如果∠FED＋__∠EFC__＝180°，那么AC∥ED；(4)如果∠2＋__∠AED__＝180°，那么AB∥DF.三、解答题(共50分)11．(8分)如图，由A地去B地再到河边l的最短线路是什么？请你画出并说明理由．解：连接AB，过点B作BC⊥l于C点，折线ABC即为所求，理由：①两点之间线段最短，②垂线段最短．图略12．(8分)如图，直线AB和CD相交于点O，OE⊥CD于点O，OD平分∠BOF，∠BOE ＝50°，求∠AOC，∠EOF，∠AOF的度数．解：∠AOC＝40°，∠EOF＝130°，∠AOF＝100°13．(10分)如图，直线AB，CD相交于点O，OE平分∠BOD，OF平分∠COE，∠2＝4∠1，求∠AOF的度数．解：由∠2＋∠BOD ＝180°，OE 平分∠BOD ，得4∠1＋2∠1＝180°，∴∠1＝30°，∠AOC ＝∠BOD ＝60°，∠COF ＝12 ∠COE ＝12 (180°－∠DOE )＝12 (180°－30°)＝75°，∴∠AOF ＝60°＋75°＝135°14．(12分)如图，已知∠B ＝∠C ，∠1＝∠D ，试问OM ∥AB 吗？为什么？解：OM ∥A B.理由：∵∠B ＝∠C ，∴AB ∥CD ，又∵∠1＝∠D ，∴CD ∥OM ，∴AB ∥OM15．(12分)如图所示，直线AB 与CD 相交于点O ，OE ⊥CD . (1)若∠BOD ＝28°，求∠AOE 的度数；(2)若OF 平分∠AOC ，小明经探究发现：当∠BOD 为锐角时，∠EOF 的度数始终都是∠BOC 度数的一半，请你判断他的发现是否正确，并说明理由．解：(1)∵∠BOD ＝28°， ∴∠AOC ＝∠BOD ＝28°. ∵OE ⊥CD ，∴∠AOE ＝∠EOC －∠AOC ＝90°－28°＝62° (2)他的发现正确，理由如下：设∠BOD ＝x ，则∠AOC ＝∠BOD ＝x ，∠BOC ＝180°－x . ∵OF 平分∠AOC ， ∴∠FOC ＝12x .∴∠EOF ＝∠EOC －∠FOC ＝90°－12 x .∴∠EOF ＝12 ∠BOC。

第一周周清试卷1、下列说法正确的个数是（ ）个（1）两条直线不相交就平行。

（2）在同一平面内，两条平行的直线有且只有一个交点（3）过一点有且只有一条直线与已知直线平行（4）平行于同一直线的两条直线互相平行（5）两直线的位置关系只有相交与平行2、完成下列推理，并在括号内注明理由。

（1）因为AB // DE ，BC // DE （已知）。

所以A,B,C 三点___________（ ）（2）因为AB // CD ，CD // EF （已知），所以________ // _________( )3、如图4，直线AB 、CD 相交于点O ，∠1=90°：则∠AOC 和∠DOB 是 角，∠DOB 和∠DOE 互为 角，∠DOB 和∠BOC 互为 角，∠AOC 和∠DOE 互为 角图5 图64.如图5所示，下列说法中正确的是（ ）A ．∠2和∠4是同位角B ．∠2和∠4是内错角C ．∠1和∠A 是内错角D ．∠3和∠4是同旁内角5、已知∠1与∠2是邻补角，∠2是∠3的邻补角，那么∠1与∠3的关系是（ ）.A 、对顶角B 、相等但不是对顶角C 、邻补角D 、互补但不是邻补角6、如图6，，直线AB 、CD 相交于点O ，OE ⊥AB 于O ，若∠COE=55°，则∠BOD 的度数为（ ）A. 40° B. 45° C. 30° D. 35°7、在同一平面内，若a ⊥b ，c ⊥b ，则a c 。

8、两直线平行，一组同位角的角平分线的位置关系是 .二、解答题：1、如图OE ⊥OF ，∠EOD 和∠FOH 互补，求∠DOH 的度数。

EO FHD 图7O DCBAE2、如图,∠ 1= ∠C ,∠ 2= ∠C ,请找出图中互相平行的直线,并说明理由.3、如图，∠1 = ∠2 = 55°， ∠3等于多少度？直线AB 、CD 平行吗？说明你的理由。

4、如图所示，∠1=75°，∠2=105°，试说明直线AB ∥CD ，5、如图6，三条直线AB 、CD 、EF 相交于点O ，∠1=75°，∠2=68°，求∠COE 的度数。

七年级第一周数学周清试卷一、选择题(每小题3分，共36分)1．中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入100元记作＋100元．那么－80元表示( )A．支出20元B．收入20元C．支出80元D．收入80元2．既是分数又是正数的是()A．＋2 B．－413C．0 D．2.33．－5的相反数是( )A．－5 B．5 C．－15D.154．－8的绝对值等于( )A．8 B．－8 C．－18D.185．如图，检测4个足球，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数．从轻重的角度看，最接近标准的是( )A B C D6．数轴上表示－2和3的两点之间的距离是( )A．1 B．2 C．3 D．57．某次数学测试的成绩若以70分为基准，老师公布的成绩为小丽＋28分，小明0分，小亮－12分，则小亮的实际分数是() A．98分B．70分C．58分D．88分8．一个数在数轴上所对应的点向左移2 016个单位后，得到它的相反数对应的点，则这个数是( )A．2 016 B．－2 016 C．1 008 D．－1 0089.数轴上表示整数的点称为整点，某数轴的单位长度是1厘米，若在这个数轴上随意画一条长16厘米的线段AB，则AB盖住的整数点的个数共有多少个( )A．13或14个B．14或15个 C．15或16个D．16或17个10．已知点M、N、P、Q在数轴上的位置如图，则其中对应的数的绝对值最大的点是( )A．M B．N C．P D．Q11．绝对值等于其相反数的数一定是()A．负数B．正数C．负数或零D．正数或零12．有理数a在数轴上的对应点的位置如图所示，则a、b、－a、|b|的大小关系正确的是( )A．|b|＞a＞－a＞b B．|b|＞b＞a＞－aC．a＞|b|＞b＞－a D．a＞|b|＞－a＞b二、填空题(每小题3分，共30分)13．如果向西走12米记作＋12米，那么－120米表示的意义是，向东走－150米表示的意义是．14．在0，|－1|，－4，－103这四个数中，是负整数的是．15．比较大小：－2.25 －|－2.5|.第 1 页第 2 页16．从数轴上表示－1的点出发，向左移动2个单位长度到点B ，则点B 表示的数是 ，再向右移动5个单位长度到达点C ，则点C 表示的数是 ． 17．化简下列各数：－(－68)＝ ，－(＋0.75)＝ ． 18．绝对值最小的有理数是 ，最大的负整数是 ． 19．在数轴上的点A 、B 位置如图所示，则线段AB 的长度为 ． 20．若|x|＝7，则x ＝ ；若|－x|＝7，则x ＝ ． 21．数轴上与原点距离为4个单位长度的点表示的数是 ．22．观察下列各数：－12，23，－34，45，－56，…，根据它们的排列规律写出第2 017个数为 ． 三、解答题(共54分) 23．(6分)化简下列各数：(1)－[＋(－0.5)]； (2)－[-(-2617)]． 24．(10分)把下列各数填在相应的大括号里：7，－45，6.8，0，56，－5.4，＋2019，－3.14，47，－19.正整数集合：{ …}； 负整数集合：{ …}； 正分数集合：{ …}; 负分数集合：{ …}．非负数集合：{ …}．25．(8分)画出数轴，并在数轴上画出表示下列各数及其相反数的点，并将这些数和它们的相反数用“＜”号连接起来：3，－4.5，113，0.26．(10分)某校七年级某班派出12名同学参加数学竞赛，这12名同学的成绩分别是90分、95分、70分、71分、72分、79分、81分、77分、78分、80分、82分、85分．(1)这12名同学成绩的平均分是多少？(2)以平均值为标准，用正数表示超出部分，用负数表示不足部分，它们对应的数分别是什么？27．(10分)北京航天研究院所属工厂，制造“神舟”10号飞船上的一种螺母，要求螺母内径可以有±0.02 mm 的误差，抽查5个螺母，超过规定内径的毫米数记作正数，没有超过规定内径的毫米数记作负数，检查结果如下：＋0.01，－0.018，＋0.026，－0.025，＋0.015.(1)指出哪些产品是合乎要求的(即在误差范围内的)?(2)指出合乎要求的产品中哪个质量好一些(即最接近规定尺寸)?28.（10分）小明到市行政中心大楼办事，假定乘电梯上一楼记作+1，向下记作-1，小明从1楼出发，电梯上下楼依次记录如下：+5，-3，+11，-8，+12，-6，a ；然后小明又回到了1楼。