第三章 恒定磁场(2)-new

三、恒定磁场电流或运动电荷在空间产生磁场。

不随时间变化的磁场称恒定磁场。

它是恒定电流周围空间中存在的一种特殊形态的物质。

磁场的基本特征是对置于其中的电流有力的作用。

永久磁铁的磁场也是恒定磁场。

1、磁通密度与毕奥－萨伐尔定律磁通密度是表示磁场的基本物理量之一，又称磁感应强度，符号为B。

电流元受到的安培力 B l d I f d⨯''=毕奥——萨伐尔定律 ⎰⨯=l r r l Id B 2004 πμ对于粗导线，可将导线划分为许多体积元dV 。

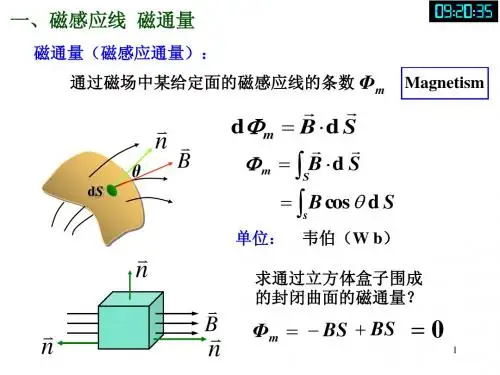
⎰⎰⎰⨯=Vrr dV J B 24 πμ 2、磁通连续性定理磁场可以用磁力线描述。

若认为磁场是由电流产生的，按照毕奥－萨伐尔定律，磁力线都是闭合曲线。

磁场中的高斯定理 0d =⋅⎰⎰SS B式中，S 为任一闭合面，即穿出任一闭合面的磁通代数和为零。

应用高斯散度定理⎰⎰⎰⎰⎰⋅∇=⋅VSdV B S B d0＝⎰⎰⎰⋅∇VdV B由于V 是任意的，故 0＝B⋅∇式中⋅∇为散度算符。

这是磁场的基本性质之一，称为无散性。

磁场是无源场。

3、磁场中的媒质磁场对其中的磁媒质产生磁化作用，即在磁场的作用下磁媒质中出现分子电流。

总的磁场由自由电流与分子电流共同产生。

永磁铁本身有自发的磁化，因而不需要外界自由电流也能产生磁场。

磁媒质的磁化程度用磁化强度M来表征，它是单位体积内的磁偶极矩。

磁偶极矩：环形电流所围面积与该电流的乘机为磁偶极矩，其方向与电流环绕方向符合右螺旋关系。

n IS P m =磁场强度 M B H-=0μ 或 )(0M H B +=μ本构方程 由m H M χ=可得 H B μ＝，该式称为磁媒质的成分方程或本构方程。

磁媒质的分类：r m μμχμμ00)1(=+=，顺磁质 1>r μ，抗磁质 1<r μ，铁磁质1>>r μ。

4、安培环路定律磁场强度H沿闭合回路的积分，等于穿过该回路所限定的面上的自由电流。

回路的方向与电流的正向按右螺旋规则选定。

1恒定磁场1．真空中位于'r点的点电荷q的电位的泊松方程为（）2．由（）可知，无界空间中的恒定磁场由恒定磁场的散度和旋度方程共同决定3．恒定磁场在自由空间中是（）场4．磁通连续性定律公式物理意义：穿过任意闭和面的磁通量为（）。

即进入闭和面S的磁力线数与穿出闭和面S的磁力线数（），磁力线是闭和的5．安培环路定律公式物理意义：磁感应强度B沿任意闭和路径l的线积分，（）穿过路径l所围面积的总电流与的乘积6．一个载流的小闭和圆环称为（）7．电流环的面积与电流的乘积，称为（）8．在远离偶极子处，磁偶极子和电偶极子的场分布是（）的，但在偶极子附近，二者场分布（）9．磁力线是（）的，电力线是间断的10．介质在磁场作用下会产生（）11．磁化引起的分子电流、原子电流相当于（）12．磁偶极子产生（）磁场，叠加于原场之上，使磁场发生变化。

磁化的结果使介质中的合成磁场可能减弱，也可能增强13．介质磁性能分类：（）磁性介质，（）磁性介质，铁磁性及亚铁磁性介质14．（）磁性介质：二次磁场与外加磁场方向相反，导致介质中合成磁场减弱15．（）磁性介质：二次磁场与外加磁场方向相同，导致介质中合成磁场增强16．铁磁性及亚铁磁性介质：在（）作用下，磁化现象非常显著17．在无传导电流的均匀介质中，束缚电流体密度为（）18．只有磁场强度为零或磁场强度与介质表面相垂直的区域，束缚电流面密度为（）19．磁感应强度通过某一表面的通量称为（）20．与某电流交链的磁通量称为（）21．导线回路的总自感等于内、外自感之（）22．单位导线回路的内自感为（）23．磁场问题的基本变量是场源变量和两个基本的场变量：磁感应强度和磁场强度。

实验证明：磁场的两个基本变量之间的关系为（）24．磁通量连续性方程微分形式：（）25．安培力可以用磁能量的空间变化率称（）来计算26．自由空间中一半径为a的无限长导体圆柱，其中均匀流过电流I，求导体内外的磁感应强度27．一段长为L的导线，当其中有电流I通过时，求空间任一点的矢量磁位及磁感应强度28．磁导率为，内外半径分别为a，b的无限长空心导体圆柱，其中存在轴向均匀电流密度，求各处磁场强度和磁化电流密度。

恒定磁场的基本方程矢量磁位磁偶极子恒定磁场中的介质恒定磁场中的边界条件电感磁场能量安培力的定律真空中，两个线电流回路安培力，说到底是磁场对运动电荷的作用力磁场对运动电荷的作用力又称洛仑兹力。

洛仑描述磁场特性的基本物理量：磁感应强度真空中的磁导率：真空中的介电常数：电磁场与电磁波线电流回路线电流分布面电流分布体电流分布一长为磁感应强度。

解：考虑到对称性，选择圆柱坐标系，导线与重合，导线中点位于坐标原点，则导线产生的磁由图可见，导线中B直接对毕奥r2015/11/6电磁场与电磁波利用散度定理和恒定磁场的散度方程利用真空中无限长直导线的磁场可得安培环路定律利用斯托克斯定理和安培环路定律，可得恒定磁场的旋度方程微分形式积分形式恒定磁场是无散场由库仑规范将矢量磁位表达式带入磁场的基本方程，得到矢量位的泊松方程：在直角坐标系中，有解由矢量磁位的表达式可以求得磁感应强度：=B 电流为磁偶极子电偶极子电偶极距磁偶极距显然，场具有轴对称性，所以矢量磁位无关。

考虑电流元Iad d φ=A =A 将其带入对于则磁感应强度磁场中放入介质，将会出现介质被磁化的现象被磁化的介质将产生附加磁场，总磁场是外磁介质被磁化的程度可以用磁化强度来衡量磁化强度：单位体积内磁偶极距的矢量和介质中的磁偶极距作为二次源产生磁场，不论是外加磁场还是二次磁场，其源都是电流。

39磁化强度同磁化电流密度有如下关系若物质内部磁化强度均匀，即自由空间的静磁场在存在外磁场的介质中，磁场由传导电流和束∇对对各项同性的线性媒质“““例：磁导率为导体圆柱，其中存在轴向均匀电流密度解：问题具有轴对称性，磁场强度只与场点与轴线的距离有关而与角向坐标无关。

利用介质中的安培环路当a束缚电流体密度r=b面上的磁化面电流密度磁感应强度由磁场强度由切向分量法向分量如果两种媒质是各项同性的线性媒质，且无界面电流，有折射规律磁链回路由步骤电流回路的外磁链所引起的自感叫外自感。

对于'Φ电流回路在导线内部的磁链所引起的自感叫内自感。

第三章 恒定电流的磁场1 学习方法：与电场平行、进行对比，即宜于理解，又复习电场。

2 内容线索：1）如何求解磁场问题？理论方面：基本方程，位函数（引入矢量位），边界条件。

应用方面：电感的计算；2）基本概念：磁场的能量§3.1恒流磁场的基本方程1 恒定电流不仅产生电场，也产生磁场。

它们都不随时间变化，即0→∂∂t ，由此可以得到恒流磁场的基本方程 微分形式：⎪⎪⎩⎪⎪⎨⎧==⋅∇=⨯∇H B B J H μ0 积分形式⎪⎪⎩⎪⎪⎨⎧==⋅⋅=⋅⎰⎰⎰H B s d B s d J l d H s c s μ0 2 恒流磁场的性质：恒流磁场的源是旋度（涡旋）源－恒定电流，即磁场是有旋场；恒流磁场没有散度源，是无源场（无散场）；磁力线成闭合曲线，它围绕着恒定电流，两者呈右手螺旋关系。

§3.2 恒流磁场的位函数分标量位和矢量位两种，一般不同时使用。

前者用于无电流区域，后者用于有电流情况1 标量位：在无电流区域，0=J ，有0=⨯∇H ，因此可以定义标量位函数，以简化磁场的计算。

标量位定义如下m H ϕ-∇=同样由0=⋅∇=⋅∇H B μ得02=-∇=∇⋅-∇=⋅∇m m H ϕϕ即标量位的拉普拉斯方程： 02=∇m ϕ标量位没有物理意义。

2 标量位的计算与标量位的参考点：定义与电位相似，只是多了电流项。

安培环路定律可得： ⎰=⋅AMBNAkI l d H 即 ⎰⎰⎰⎰+⋅=⋅⇒=⋅+⋅A N BA MB A M B B N A kI l d H l d H kI l d H l d H 由此可见任意两点之间磁场不同路径的线积分，其结果仅相差一个常数项（恒定电流），求导后不影响磁场的计算结果。

又因为⎰-=⋅AMB mB mA l d H ϕϕ ，令B 为标量磁位参考点，即0=mB ϕ则 ⎰+⋅=AXB mAkI l d H ϕ 积分路径AXB 指A 点到B 点的任意路径。

3 恒流磁场的矢量位：矢量位既可以用于无电流的区域，也可以用于有电流的区域。