储量计算的算术平均法

矿产储量计算
第一节 概述
一、概念 二、矿产储量的单位
三、储量计算过程
1、圈定矿体、计算参数 2、计算体积
V S mS : 矿体面积；m 矿体平均厚度
V＝S

m
S：矿体的水平或垂直投
影面积
m：矿体的水平或垂直方向 平均厚度
3、计算矿石量
Q V D矿石的平均体重 t / m3
二、矿体边界线的确定ຫໍສະໝຸດ 法（一）零点边界线的确定方法 （二）可采边界线的确定方法
（三）矿石类型与矿石品级边界线的确定 据地质因素、矿化规律来确定。
氧化矿石
氧化矿石
A:不正确
原生矿石
原生矿石
B:正确
块状矿石
地下水面
块状矿石
浸染状矿石
A:不正确
浸染状矿石
B:正确
矿产储量计算
第一节 概述 第二节 矿产工业指标
矿产储量计算
第一节 概述
通一过、一概系念列的找矿工作，对矿床进行大规模的
坑1、探矿、产钻储探量工作，按照取样原则进行大量的取 样指矿工产作在，地并下对的施埋工藏的量工程开展地质编录工作， 至2、此矿，产我储们量较（为资精源确量地）了计解算了：矿体的空间分布 规据各律种、探矿矿石工的程质和量技。术完手成段以所上得工到作的之资后料，（好信像 是息）十，月通怀过胎一，定最的后计要算有方所法收计获算，矿那产么的我地们下最埋后 的藏量收，获这就一是系矿列产的工资作源称量之，矿也产就储是量说（矿资产源勘量查） 的计算目的就是查明矿产的质量，最后作为生产部 门矿产开储展量生计产算的是依整据个。矿产勘查工作的成果总结， 一般在矿产勘查的各个阶段都要进行此项工作， 但资源量的级别有所区别。
第一节 概述 第二节 矿产工业指标

金属、非金属矿产储量计算方法邓善德(国土资源部储量司)一、储量计算方法的选择矿体的自然形态是复杂的，且深埋地下，各种地质因素对矿体形态的影响也是多种多样的，因此，我们在储量计算中只能近似的用规则的几何体来描述或代替真实的矿体，求出矿体的体积。

由于计算体积的方法不同，以及划分计算单元方法的差异，因而形成了各种不同的储量计算方法在。

比较常用的方法有：算术平均法，地质块段法，开采块段法，多角形法(或最近地区法)，断面法(包括垂直剖面法和水平断面法)及等值线法等，其中以算术平均法、地质块段法、开采块段法和断面法最为常见。

现将几种常用的方法简要说明如下。

1.算术平均法是一种最简单的储量计算方法，其实质是将整个形状不规则的矿体变为一个厚度和质量一致的板状体，即把勘探地段内全部勘探工程查明的矿体厚度、品位、矿石体重等数值，用算术平均的方法加以平均，分别求出其平均厚度、平均品位和平均体重，然后按圈定的矿体面积，算出整个矿体的体积和矿石的储量。

算术平均法应用简便，适用于矿体厚度变化小，工程分布比较均匀，矿产质量及开采条件比较简单的矿床。

2.地质块段法它是在算术平均法的基础上加以改进的储量计算方法，此方法原理是将一个矿休投影到一个平面上，根据矿石的不同工业类型、不同品级、不同储量级别等地质特征将一个矿体划分为若干个不同厚度的理想板状体，即块段，然后在每个块段中用算术平均法(品位用加权平均法)的原则求出每个块段的储量。

各部分储量的总和，即为整个矿体的储量。

地质块段法应用简便，可按实际需要计算矿体的不同部分的储量，通常用于勘探工程分布比较均匀，由单一钻探工程控制，钻孔偏离勘探线较远的矿床。

地质块段法按其投影方向的不同垂直纵投影地质块段法，水平投影地质块段法和倾斜投影地质块段法。

垂直纵投影地质块段法适用于矿体倾角较陡的矿床，水平投影地质块段法适用于矿体倾角较平缓的矿床，倾斜投影地质块段法因为计算较为繁琐，所以一般不常应用。

矿产资源储量的计算方法
矿产资源储量的计算方法有多种，常用的包括断面法、算术平均法、地质块段法、开采块段法、三角形法及最近地区法等。

在计算过程中，首先需要根据矿床地质特点和所用勘探方法，选择合理的储量计算方法。

然后在各种综合图上根据工业指标圈定矿体边界，划分矿体块段，计算各块段的平均厚度、平均品位、矿石密度、矿体面积以及含矿系数等参数。

最后按公式计算块段金属储量，累计块段金属储量为矿体（或矿床）金属储量。

以上内容仅供参考，如需更多信息，建议查阅相关文献或咨询地质专家。

几种常见的矿产资源储量估算方法固体储量估算方法主要是几何法和统计分析法。

一、几何法（一）断面法（剖面法）原理就是当矿体被一系列勘查断面横切为若干块段，就可以以这些断面图为基础，估算相邻两断面间的矿块储量乃至整个矿床储量。

分为垂直断面法和水平断面法。

第一步：计算体积1、当相邻两断面的矿体形状相似，且其相对面积差（S1－S2）÷S1小于40%时，用梯形体积公式V=(S1+S2)×L÷2。

其中V为两断面间的矿体体积；L为相邻两剖面间的距离；S1、S2为相邻两端面上的矿体面积。

2、当相邻两断面的矿体形状相似，且其相对面积差（S1－S2）/S1大于40%时，选用截锥体积公式，即V=（S1+S2+√S1×S2）×L÷3。

其中V为两断面间的矿体体积；L为相邻两剖面间的距离；S1、S2为相邻两端面上的矿体面积。

3、当相邻两断面的矿体形状不同，不论面积相差多少，除油一对应边相等时，可用梯形体积公式外，其余均应选用似角柱体（辛浦生）公式，即V=[（S1+S2）÷2+2S m]×L÷3 =（S1+S2+4S m）×L÷6。

其中V为两断面间的矿体体积；L为相邻两剖面间的距离；S1、S2为相邻两端面上的矿体面积。

S m为似角柱体的平均断面面积。

4、当在相邻的两剖面中只有一个剖面有面积，而另一剖面上矿体已尖灭，或矿体两段边缘部分的块段只有一个断面控制时，其体积计算可根据剖面上的矿体面积形状或矿体尖灭特点不同选择不同公式。

（1）当矿体作楔尖灭时，块段体积用楔形公式计算。

V=L×S÷2（2）当矿体作锥形尖灭时，块段体积可用锥形公式计算。

V=L×S÷3第二步，计算两剖面间块段的矿石储量Q=V×d。

其中Q为块段矿石储量，V为块段的矿体体积，d为块段矿石平均体重。

第三步，计算出两剖面间块段的金属储量P=Q×C。

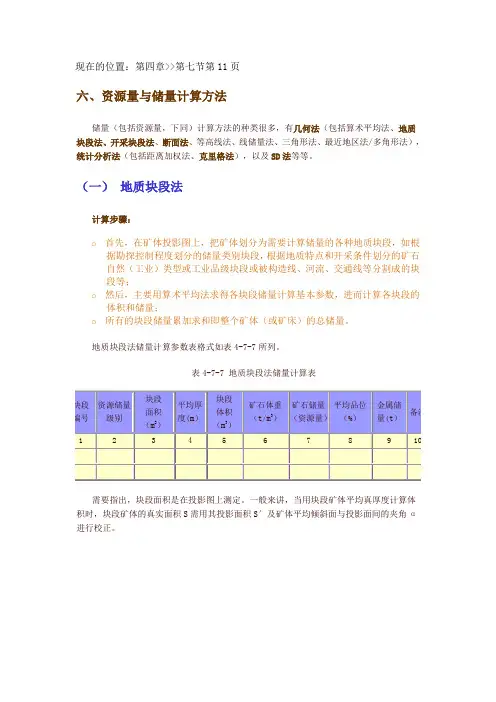
现在的位置：第四章>>第七节第11页六、资源量与储量计算方法储量（包括资源量，下同）计算方法的种类很多，有几何法（包括算术平均法、地质块段法、开采块段法、断面法、等高线法、线储量法、三角形法、最近地区法/多角形法），统计分析法（包括距离加权法、克里格法），以及SD法等等。

（一）地质块段法计算步骤：o首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等；o然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；o所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表4-7-7所列。

表4-7-7 地质块段法储量计算表需要指出，块段面积是在投影图上测定。

一般来讲，当用块段矿体平均真厚度计算体积时，块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。

在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图4-7-3 在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图； (c)、(d)—立体图1—矿体块段投影； 2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

缺点：误差较大。

当工程控制不足，数量少，即对矿体产状、形态、内部构造、矿石质量等控制严重不足时，其地质块段划分的根据较少，计算结果也类同其他方法误差较大。

浅谈露天矿山资源储量的计算方法近年来随着测绘技术及开采技术的不断提高，在露天矿山开采中，矿山资源储量的计算要求也越来越高，本文就露天矿的资源储量各种计算方法进行阐述和优缺点分析。

标签：露天矿;资源储量;计算方法露天矿和洞采矿在矿山资源量计算方法中有很大区别，相对来说露天矿的计算方法比较多，其中总结下来说有几何法（包括算术平均法、地质块段法、开采块段法、断面法等），统计分析法（包括距离加权法、克里格法），以及SD法等等。

本文就露天矿中资源储量的计算方法来做阐述及个人分析优缺点。

1、几何法1.1算数平均法算术平均法的原理就是通过高数原理将整个需要计算的区域中形状不规则的矿体变为一个或者分成几个厚度和质量一致的板状体，即把区域内全部勘探工程查明的矿体厚度、品位、矿石体重等数值进行有效的平均，计算出其算术平均厚度平均哦、品位和平均体重，如果分成一个区域直接算出整个矿体体积和矿产的储量，如果分成几个区域，几个区域再取平均数，计算出整个矿体体积和矿产的储量。

优点：算术平均法计算储量，过程简单，计算简单，图纸简单缺点：由于是取平均数，它只能适用于矿体厚度变化较小、品味变化不大，勘探工程在矿体上的分布较为均匀、矿产质量及开采条件比较简单的矿床。

如果勘探工程分布得不均匀，品位变化很大，矿化又很不均匀时，计算误差很大程度可能变大。

对于勘探程度较低的矿床，常常应用此方法。

1.2地质块段法地质块段法的原理和算數平均法分段求平均再相加原理相近，不过计算的内容主要包括地块面积，平均厚度，地块体积，矿石体重，矿石储量，平均品位，成品储量等。

优点：通过分段来计算，适用性强。

因为矿山形状，走向都不会相同，用分块法很好的解决这问题，而且不需另作复杂图件、计算方法简单并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

（1）、计算单元内有岩芯分析资料，且代表性较好，其 有效孔隙度取岩芯分析值。
（2）、计算单元内无岩芯分析资料，有效孔隙度采用经 验公式计算值。
目前均借用最新储量报告取值。
4、原始含油饱和度---So， %（取整）
（1）、利用油基泥浆取芯实验室获得。 （2）、若无油基泥浆取芯，采用阿尔奇经验公式法和半 渗透隔板法等。
1、含油边界圈定---A， Km2 ：
根据钻井、测井和试油等资料，在平面构造图上圈定含油面 积。圈定原则如下：
（1）、断块油藏按相应层位的构造图圈定பைடு நூலகம்断层线控制含 油边界；
（2）、以构造为主要因素的含油边界圈定原则： 一是当含油边界有油水同层井点控制时，含油边界线
可通过构造最低部位的油水同层井点，并平行于构造等高线圈 定含油面积。
尖灭井
含油边界线
油井 尖灭线
干井
2、平均有效厚度---h ，ｍ
有效厚度划分： 顶底界面的确定---采用以自然伽玛、微电极、深浅 侧向测井曲线为主，参考微球等其它曲线划分有效厚 度。以自然伽玛、深浅侧向半幅点和微电极幅度差的 异常点，结合微球电阻率下降对应点确定油层顶底界 面，起划厚度0.4m。
夹层扣除：夹层有两种，即泥岩夹层和灰质夹层。
石油地质储量计算
一、储量计算公式 ：
采用容积法进行储量计算：
Ｎ＝100×Ａ×ｈ×Φ×So×ρ。／Boi
A --- 含油面积，Km2 h --- 平均有效厚度，ｍ Φ--- 平均有效孔隙度，% So--- 含油饱和度，%（取整） ρ。— 地面原油密度，g/cm3 Boi— 原油体积系数 N — 石油地质储量，104t
二是含油边界无油水同层井点控制时，含油（气）边 界线可通过相距最近的油井与水井间距之半处或外推一根等高 线（50m），并平行于构造等高线圈定。

储量计算的算术平均法[导读]算术平均法的实质是将整个形状不规则的矿体变为一个厚度和质量一致的板状体，即把勘探地段内的全部勘探工程查明的矿体厚度、品位、矿石体重等数值，用算术平均法加以平均，分别求出其算术平均厚度平均评为和平均体重，然后按圈定的矿体面积算出整个矿体体积和矿产的储量。

算术平均法的实质是将整个形状不规则的矿体变为一个厚度和质量一致的板状体，即把勘探地段内的全部勘探工程查明的矿体厚度、品位、矿石体重等数值，用算术平均法加以平均，分别求出其算术平均厚度平均评为和平均体重，然后按圈定的矿体面积算出、整个矿体体积和矿产的储量（图1）。

图1 用算术平均法计算储量把复杂矿体变为简单板状体a－勘探剖面；b－计算时变为等面积的简单矿体的剖面；c－计算后的简单板状矿体矿体的体积圈定范围内按下式计算：V＝S·（1）式中：V－矿体的体积；S－矿体的面积；－矿体的平均厚度。

间带（边缘工程到外边界线的面积）的矿体体积按下式计算：式中：V m－间带的矿体体积；k－内边界线上见矿平均厚度；m n－外边界线上采用的最小可采厚度；S m－内外边界线之内的矿体面积。

矿产的矿石储量按下式计算：Q＝V·式中：Q－矿石储量；－矿石的平均体重。

有用组分的金属量按下式计算：P＝Q·式中：P－金属的重量；－矿石中有用组分平均品位。

用算术平均法计算储量时，确定矿体平均厚度及平均品位按表1及表2进行。

表1表2算术平均法计算储量，过程简单，不需作复杂的图纸是其优点，但是，它只能应用于矿体厚度变化较小、勘探工程在矿体上的分布较为均匀、矿产质量及开采条件比较简单的矿床。

如果勘探工程分布得不均匀，矿化又很不均匀时，可能产生较大的误差。

对于勘探程度较低的矿床，常常应用此方法。

储量计算参数的确定之矿⽯平均品位计算储量计算参数的确定三、矿⽯平均品位计算每个样品的品位是据化学分析结果得来的，储量计算时须计算出矿⽯的平均品位。

下⾯分单⼯程、断⾯、块段和矿体分别计算。

(⼀)单⼯程平均品位计算单个⼯程中(钻孔、穿脉、浅井、探槽等)的平均品位计算，常⽤算术平均法和加权平均法。

具体计算⽅法与平均厚度计算相似。

(⼆)断⾯平均品位计算⼀般采⽤加权平均计算，计算⽅法如下：同理，也可⽤样品控制长度加权(图2-6-19)，甚⾄以样品控制长度和厚度两参数之乘积联合加权(图2-6-20)。

(三)块段平均品位计算块段平均品位计算有两种：(1)对于品位变化不⼤的块段，多采⽤算术平均法。

(2)对于品位变化与某些因素(如厚度、⾯积)相关，⼀般以影响因素作权数，进⾏加权平均(图2-6-21)。

其计算公式如下：(四)矿体平均品位计算矿体平均品位计算，可⽤块段体积与品位加权计算，也可⽤算术平均法计算。

(五)特⾼品位的确定与处理当某些样品的品位⾼出⼀般样品品位很多倍，这样的品位称为特⾼品位。

这种情况是由个别样品取于矿化局部富集的地⽅⽽产⽣的。

由于特⾼品位的存在会引起平均品位的剧烈增⾼，因此在平均品位计算时，必须对特⾼品位进⾏处理。

为了检验特⾼品位是否属实，要对样品的化验、取样进⾏慎重分析、检查。

如确为特⾼品位，处理⽅法有以下⼏种：(1)计算平均品位时，把特⾼品位除去。

(2)⽤特⾼品位的两相邻样品的平均品位代替特⾼品位。

(3)⽤特⾼品位范围内的块段或断⾯平均品位代替特⾼品位。

(4)⽤⼀般品位的最⾼值代替特⾼品位。

(5)⽤统计法统计不同级别的频率，即求出每⼀级样品品位数量与样品总数之⽐，也就是样品率，然后再⽤每⼀级样品率去加权计算平均品位。

实际⼯作中，特⾼品位往往是客观存在的，应结合矿区特点进⾏综合分析，对特⾼品位产⽣的原因，要认真检查和研究，如确系富矿引起，则特⾼品位不应⼈为地除去，应当参加计算。

油+水+岩石膨胀 侵入水 出水量
We--累积天然水侵量，104m3 WP--累积产水量，104m3 Bw--在P压力下地层水的体积系数
整理后得该油藏原始地质储量：
N P Bo We WP Bw N Boi Ct P
弹性水压驱动油藏 物质平衡方程式的建立
⑴ 正常压力条件下的封闭型气藏
该类气藏的驱气动力为：天然气本身的弹性膨胀力。 根据孔隙体积守恒原理，气藏从原始地层压力Pi降至 某一压力P时，气藏内流体所占孔隙体积变化如下图：
GB gi (G G p ) Bg We W p Bw
G G P Bg We WP Bw Bg Bgi
We--累积天然水侵量，108m3 WP--累积产水量，108m3
弹性水压驱动气藏物质平衡方程式的建立
封闭型气藏物质平衡方程：
GBgi (G G p ) Bg
实际气体所占体积与相同数量气体理想状态下体积的比值。
G
G p Bg Bg Bgi
pS ZT Bg pTS
pS Z iTi Bgi piTS
p pi G p 1 Z Zi G
pi--原始地层压力，MPa pS--地面标准压力，MPa Ti--原始地层温度，K
2、储量计算参数的平均方法 (1) 油层有效厚度平均值 ① 算术平均法
h
hi
i 1
n
h
n
--平均有效厚度，m hi--单井油层组有效厚度，m n--井数。
h
h A
i 1 n i
n
i
h --纯含油区平均有效厚度，m
Ai--各井点的单井控制面积，km2 hi--单井油层组有效厚度，m n--井数。

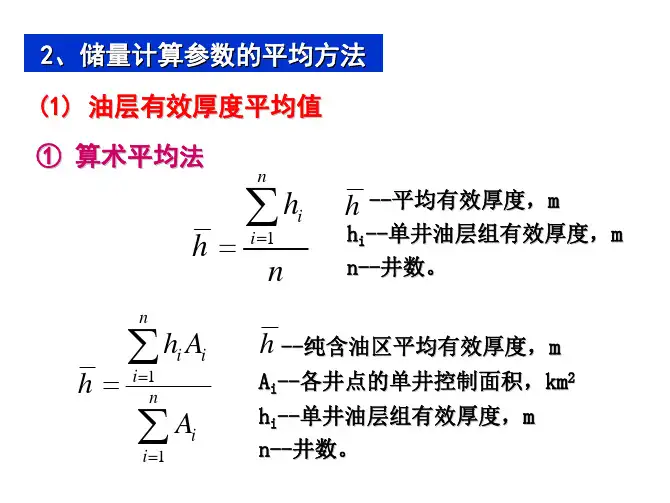
矿产资源/储量估算参数平均值计算矿产资源/储量估算时，一般要求分矿体或分块段估算。

而勘查过程中测定的参数值数量较多，因而要计算出单个工程中整个矿块乃至整个矿床该参数的平均值（如平均厚度、平均体重、平均品位等）。

参数平均值计算有算术平均和加权平均两种方法。

一、算数平均法该方法适用于矿体参数变化较小、测点分布较均匀（采样间距和长度基本相等或接近），或该参数与其他参数无任何相关关系时，其实质就是将每一个测点观测值所起的作用看做是同等的。

也就是将所有观测值加和再除以观测点数得出的平均值。

二、加权平均法当矿体参数变化较大，且测点分布不均或该参数与某一因素有相关关系，则应以这一因素为权数，以加权平均法来确定参数平均值，即不能将每一个测点所起的作用等同看待。

具体有以下几种情况：A 单个工程的平均品位计算（线平均）1）当采样间距大致相等，而矿体品位变化与厚度的变化具有一定关系时，用各采样点的厚度进行加权，计算公式如下：C= C1m1+C2m2+C3m3+.......+C n m nm1+m2+m3+......+m n式中：C为平均品位，C1、C2.........，C n为单个样品品位；m1、m2......m n为单个采样点矿体的厚度。

2）如果采样间距不等，品位变化变化较大且与厚度无明显关系时，可用每个样品的控制距离进行加权平均，其公式如下：C=C1L1+C2L2+C3L3+.......+C n L nL1+L2+L3+......+L n式中：C为平均品位；L1、L2......L n为每个样品控制距离（一般为相邻两个样品距离的一半之和）；C1、C2.........，C n为每个样品品位。

3）当矿体厚度和采样间距不等，且它们与品位成正比例关系时，用每个用品控制长度和矿体厚度之乘积联合加权计算，其公式为：C= C1L1m1+C2L2m2+C3L3m3+.......+C n L n m nL1+L2+L3+......+L n式中：C为平均品位；L1、L2......L n为每个样品影响长度；m1-m n为每个采样点矿体厚度。

图8-28似角柱体中间断面求法 (n)多角形断面；(6)圆滑曲线断面
•
• • • •
2．当矿体只有一个剖面控制时，另一 剖面上矿体已尖灭，其体积计算可选用以 下公式： (1)当矿体作楔形尖灭时(图8-29)，可用 楔形公式计算体积，即 V=1/2L x S (8-18) 式中L——两剖面间距离，或剖面到尖灭点 间距离； S——剖面上矿体面积。
• •
五、SD法 SD储量计算法是适应我国实际情况、 博采国内外储量计算方法之众长，由我国 科技人员创立和命名的一套全新的系列储 量计算和审定方法。
•
• •
SD代表3种含义： (1)它是结构曲线(structure curve)积分计算和 动态分维审定的矿产资源储量计算方法，取结构 曲线中函数的第一个字母s和动态分维几何学一词 汉语拼音的第一个字母D，即“SD‘’； D SD‘’ • (2)SD法计算过程，主要采用搜索递进法，取 “搜索”一词汉语拼音的第一个字母S，取“递 进”一词汉语拼音的第一个字母D，亦即“SD‘’； • (3)SD法具有从定量角度审定储量的功能，取 “审定”两个字汉语拼音的第一个字母，亦即 “SD'’。
•
SD储量计算方法，是既不同于传统法 亦有别于地质统计学的全新创造的矿产储 量计算方法。它从一个新的角度提出SD分 数维和结构地质变量概念、SD样条函数、 SD复杂度函数而建立的一套动态储量计算 及储量审定计算法。包括普通SD法、SD搜 索递进法、SD任意块段法、框架SD法和 SD精度法等方法。
•
•
算术平均法计算储量的优点是方法简单， 不需作复杂图纸，适用于矿体厚度变化较 小、勘探工程分布比较均匀、矿产质量及 开采条件比较简单的矿体。这种方法多用 于矿产调查初期阶段。

资源量与储量计算方法资源量与储量计算方法储量（包括资源量，下同）计算方法的种类很多，有几何法（包括算术平均法、地质块段法、开采块段法、断面法、等高线法、线储量法、三角形法、最近地区法/多角形法），统计分析法（包括距离加权法、克里格法），以及SD法等等。

（一）地质块段法计算步骤：1.首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等；2.然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；3.所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表下所列。

表地质块段法储量计算表块段编号资源储量级别块段面积（m2）平均厚度(m）块段体积（m3）矿石体重（t/m3）矿石储量（资源量）平均品位（%）金属储量(t）备注12345678910需要指出，块段面积是在投影图上测定。

一般来讲，当用块段矿体平均真厚度计算体积时，块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。

在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图； (c)、(d)—立体图1—矿体块段投影； 2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

估算矿产资源/储量的方法
一、几何图形法
1、断面法：
（1）平行断面法
①梯形公式 V=L/2(S1+S2)
②截锥公式
③锥体公式 V=SL/3
④楔形公式 V=SL/2
⑤似柱体公式 V=L/6（2a1b1+b1a2）
（2）不平行断面法
2、算术平均法
3、地质断面法
4、开采块段法
5、等高线法
二、SD法
以最佳结构地质变量为基础，以断面构形替代空间构形为核心，以 spline函数及分维几何学为工具的估算方法，立足于传统的断面法。

它适用于不同矿床类型、矿体规模、产状、不同矿产勘查阶段，还可对估算的成果作精度预测。

三、地质统计学法
是以区域化变量理论作为基础，以变异函数作为主要工具，对既具有随机性、又具有结构性的变量进行统计学研究，估算时能充分考虑品位的空间变异性和矿化强度在空间的分布特征，使估算结果更加符合地质规律，置信度高，但需有较多的样本个体为基础。

勘查过程中，针对矿床的地质特征，运用这种方法，还能制定或检验合理的勘探工程间距。

有距离加权法、相关分析法、克里格法。

内蕴经济资源量是矿产资源勘查工作自普查至勘探，地质可靠程度达到了推断的至探明的，但可行性评价工作只进行了概略研究，由于技术经济参数取值于经验数据，未与市场挂钩，区分不出其真实的经济意义，统归为内蕴经济资源量。

可细分为3个类型：
探明的内蕴经济资源量(331)
控制的内蕴经济资源量(332)
推断的内蕴经济资源量(333)。

固体矿产储量计算矿体的自然形态是复杂的，且深埋地下，各种地质因素对矿体形态的影响也是多种多样的，因此，我们在储量计算中只能近似地用规则的几何体来描述或代替真实的矿体，求出矿体的体积。

由于计算体积的方法不同，以及划分计算单元方法的差异，因而形成了各种不同的储量计算方法。

比较常用的方法有：算术平均法，地质块段法，开采块段法，多角形法(或最近地区法)断面法(包括垂直剖面法和水平断面法)及等值线法等。

其中以算术平均法、地质块段法、开采块段法和断面法最为常见。

现将常用的几种方法简要说明如下。

1.1 算术平均法是一种最简单的储量计算方法。

其实质是将整个形状不规则的矿体变为一个厚度和质量一致的板状体，即把勘探地段内全部勘探工程查明的矿体厚度、品位、矿石体重等数值，用算术平均的方法加以平均，分别求出其算术平均厚度、平均品位和平均体重，然后按圈定的矿体面积，算出整个矿体的体积和矿石的储量。

算术平均法应用简便，适用于矿体厚度变化较小、工程分布比较均匀，矿产质量及开采条件比较简单的矿床。

1.2 地质块段法它是在算术平均法的基础上加以改进的储量计算法，此方法原理是将一个矿体投影到一个平面上，根据矿石的不同工业类型、不同品级、不同储量级别等地质特征将一个矿体划分为若干个不同厚度的理想板块体，即块段，然后在每个块段中用算术平均法 (品位用加权平均法)的原则求出每个块段的储量。

各部分储量的总和，即为整个矿体的储量。

地质块段法应用简便，可按实际需要计算矿体不同部分的1储量，通常用于勘探工程分布比较均匀，由单一钻探工程控制，钻孔偏离勘探线较远的矿床。

地质块段法按其投影方向的不同又分为垂直纵投影地质块段法，水平投影地质块段法和倾斜投影地质块段法。

垂直纵投影地质块段法适用于矿体倾角较陡的矿床，水平投影地质块段法适用于矿体倾角较平缓的矿床，倾斜投影地质块段法因为计算较为繁锁，所以一般不常应用。

1.3 开采块段法是以坑道为主要勘探手段的矿床中常用的储量计算方法。

石油和天然气储量计算石油与天然气储量：是指埋在地下的石油和天然气的数量。

第一节 工业油气流标准工业油气流标准：包括油气井的工业油气流标准和储集层的工业油气流标准。

油气井的工业油气流标准：指油气井的产油气下限。

储集层的工业油气流标准：指工业油气井内储集层的产油气下限，也就是有效厚度的测试下限。

表8-1工业油气流暂行标准（1988）第二节 油气储量的分类与分级一、 分类：⎩⎨⎧)(:)(:R N N 量下可以采出来的石油储在现有的经济技术条件可采储量储量地下油层中油气的实际地质储量 采收率≈N N R二、 远景资源量及储量的分级1．远景资源量：根据地质、地震、地球化学等资料统计或类比估算的尚末发现的资源量。

（1）推测资源量：根据区域资料，结合盆地或凹陷物探普查或参数井的储集层物性和生油岩有机化学资料估算的资源量。

（2）潜在资源量：（圈闭法远景资源量）1． 预测储量→预探是在地震详查以及其他方法提供的圈闭内，经过预探井钻探获得油气流、油气层或油气显示后，根据区域地质条件分析和类比的有利地区按容积法估算的储量。

2． 控制储量：→详探钻了少数评价井后所计算的储量。

3．⎪⎩⎪⎨⎧→探明已开发储量末开发探明储量过渡基本探明储量开发阶段探明储量)( 第三节 石油储量计算法—容积法一、 原理及公式：容积法计算油气储量的实质是计算地下岩石孔隙中油气所占的体积，然后用地面的重量单位或体积单位表示。

oio o e B S he F N ρϕ⋅⋅⋅⋅= N ——地质储量，万吨；F ——含油面积，km 2He ——平均有效厚度，mφ——平均有效孔隙度，小数S O ——含油饱和度，ρO ——平均地面脱气原油密度，B Oi ——平均地面原油体积系数。

二、 参数的确定：1． 含油面积：⎪⎩⎪⎨⎧--过渡带油水界面储层尖灭线油层顶面构造图 （1）油水界面的确定1） 打到油水界面上的井（取芯资料）判断；2） 测井（SP 、Rt ）3） 油井、水井深度判断4） 压力值：1口井获得工业油流，另一口井打到油层的含水部分。

目前已有的储量计算方法很多，下面着重介绍找矿，评价阶段常用的算术平均法和地质块段法。

（一）算术平均法该法的实质是把形态不规则的矿体，改变为一个理想的具有同等厚度的板状体，其周边就是矿体的边界。

计算方法是先根据探矿工程平面图（或投影图）上圈出矿体边界，测定其面积（若为投影面积，需换算成真面积。

见后面块段法的面积换算）。

然后用算术平均法求出矿体的平均厚度、平均品位、平均体重。

最后按下面公式计算：矿体体积：V＝SxM式中：V一矿体体积（下同）；S一矿体面积；M一矿体平均厚度。

矿石储量: Q＝VxD式中：Q一矿石储量（下同；D一矿石平均体重。

矿体金属储量：P=QxC式中：P一金属储量: C一矿石平均品位。

（二）地质块段法地质块段法实际上是算术平均法的一种，其不同之处是将矿体按照不同的勘探程度、储量级别、矿床的开采顺序等划分成数个块段，然后按块段分别计算储量，整个矿体储量即是各块段储量之和。

具体计算方法是首先根据矿体产状，选用矿体水平投影图（缓倾斜矿体）或矿体垂直纵投影图，在图上圈出矿体可采边界线，按要求划分块段。

然后分别测定各块段面积S (系矿块投影面积），根据各探矿工程所获得的资料，用算术平均法计算每个块段的平均品位C，平均体重D和平均厚度M（为平均视厚度，即垂直或水平厚度）。

因为矿体的真面积与真厚度之乘积等于投影面积与投影面之法线厚度之积具体按下面步骤计算：1．块段体积：V＝S x M如果测定的面积为块段的垂直投影面积，则块段平均厚度M为块段的水平厚度；若测定的面积为块段的水平投影面积，则块段平均厚度为矿块的垂直厚度。

2．块段的矿石量：Q＝V XD3．块段的金属量：P＝QxC矿体的总储量即为各块段储量之和。

如果计算时采用的矿体平均厚度为真厚度，而面积是测定的投影面积，这时应把真厚度换算成视厚度（即水平或垂直厚度）。

或者将投形面积换算成矿体的真面积。

面积换算公式如下：S= Sˊ/sinβ式中：S一矿块真面积；Sˊ一矿块投影面积；β一矿体倾角。