投影法概念.点的投影
- 格式:doc
- 大小:62.50 KB
- 文档页数:7




投影法概述1. 概念投影法是一种用于表示三维物体的方法,通过将物体的各个点沿着特定方向投射到一个平面上,得到该物体在平面上的二维投影。
投影法可以分为平行投影和中心投影两种,其中平行投影是指投影线与平面平行,而中心投影是指投影线与平面相交于一点。
2. 原理平行投影的原理是将物体上的各个点沿着垂直于平面的方向投射到平面上,形成一个与物体相似但尺寸变小的图像。
中心投影的原理是将物体上的各个点沿着射线的方向投射到平面上,形成一个与物体相似但尺寸变小的图像。
投影过程中,需要注意投影方向、投影距离和投影比例等因素。
3. 应用投影法在工程、建筑、艺术等领域有广泛的应用。
在工程领域,投影法常用于绘制工程图纸、设计产品模型等。
在建筑领域,投影法可以用于绘制建筑平面图、立面图、剖面图等。
在艺术领域,投影法可以用于绘画、雕塑等创作过程中,帮助艺术家更好地表达物体的形状和特征。
4. 优点投影法具有简单易学、表达准确、节省空间等优点。
通过投影法,可以将复杂的三维物体用简洁的二维图像表示,使得观察者更容易理解物体的形状和结构。
同时,投影法可以节省绘图空间,使得绘图更加方便和高效。
5. 缺点投影法的缺点主要体现在失真和信息丢失方面。
由于投影法将三维物体投影到二维平面上,必然会引入一定的失真,使得物体的形状和比例在投影中发生变化。
此外,投影法也会导致部分信息的丢失,无法完全表达出物体的所有特征。
投影法是一种常用的图形表示方法,通过将三维物体投影到二维平面上,用以展示物体的形状和特征。
投影法有平行投影和中心投影两种形式,广泛应用于工程、建筑、艺术等领域。
虽然投影法存在一定的失真和信息丢失,但其简洁易学、准确表达等优点使其成为一种重要的图形表示方法。


点的投影是几何学中的一个重要概念,它常用于计算三维空间中一个点在某个平面上的投影坐标。
点的投影不仅在计算机图形学和计算机视觉中广泛应用,也在建筑设计、工程测量和机器人导航等领域发挥着重要作用。
本文将从基本概念、计算方法以及应用场景等方面对点的投影进行总结和讨论。
一、基本概念点的投影是指一个三维空间中的点在一个平面上的映射坐标。
在点的投影中,我们通常有一个三维空间中的点P(x, y, z),以及一个平面,该平面可以通过一个法向量来定义。
点P在平面上的投影称为投影点,通常用P’来表示。
二、计算方法计算点在平面上的投影坐标可以使用向量和几何知识来实现。
下面是一种常用的计算方法:1.首先,我们需要确定平面的法向量N(nx, ny, nz)以及平面上的一个点Q(qx, qy, qz)。
可以通过法线和平面上的一点来得到平面的方程。
2.然后,我们根据点P和平面上的点Q之间的向量差来计算投影向量V(vx, vy, vz)。
投影向量是点P和平面上的点Q之间的向量差,可以用PQ向量减去法向量N的投影在PQ上的分量得到。
3.接下来,我们可以通过投影向量V和平面上的点Q,使用向量加法的性质来计算投影点P’的坐标。
投影点P’的坐标可以表示为P’ = Q + V。
三、应用场景点的投影在许多领域中都有广泛的应用。
下面我们将介绍一些常见的应用场景。
1.计算机图形学:在计算机图形学中,点的投影是渲染和可视化的基础。
通过计算三维场景中物体的投影坐标,可以将其呈现在二维屏幕上,实现逼真的虚拟现实效果。
2.计算机视觉:在计算机视觉中,点的投影常用于目标检测和跟踪。
通过计算摄像机观察到的物体在图像上的投影位置,可以实现对物体的识别和定位。
3.建筑设计:在建筑设计中,点的投影常用于确定建筑物的阴影位置和日照分析。
通过计算太阳光线在建筑物上的投影坐标,可以帮助设计师优化建筑物的布局和朝向。
4.工程测量:在工程测量中,点的投影可用于测量物体的高度和位置。


点直线平面投影知识点投影是几何学中的一个重要概念,它描述了一个物体在某个平面上的阴影或映像。
在几何学中,我们经常需要计算点、直线或平面在一个给定平面上的投影,以便更好地研究物体的形状和位置。
本文将介绍点、直线和平面在投影过程中的一些基本知识点。
1.点的投影点的投影是指一个点在一个给定平面上的映像。
当我们将一个点垂直投影到一个平面上时,投影点与原点和投影平面上的点构成的直线相垂直。
我们可以使用垂直投影的概念来计算点的投影坐标。
2.直线的投影直线的投影是指一个直线在一个给定平面上的映像。
当直线与投影平面垂直时,其投影为一条线段,两者之间的关系是平行的。
当直线与投影平面不垂直时,其投影为一个线段或线段的集合,我们可以使用投影法来计算直线的投影。
3.平面的投影平面的投影是指一个平面在一个给定平面上的映像。
我们可以使用平行投影或透视投影来计算平面的投影。
平行投影时,平面的投影与原平面平行,透视投影时,平面的投影会根据视点的位置而有所变化。
4.投影的性质投影的性质是指投影过程中的一些重要特点。
首先,投影不改变物体之间的相对位置关系,即在投影平面上两个点的距离与它们在原物体上的距离相等。
其次,正交投影保持直线的直线性质,即投影线段仍然是直线。
最后,平行投影保持平面的平面性质,即投影平面上的点仍然在同一个平面上。
综上所述,点、直线和平面的投影是几何学中的基本概念。
了解投影的计算方法和性质可以帮助我们更好地理解物体的形状和位置。
通过使用适当的数学方法和工具,我们可以计算出物体在给定平面上的投影,从而更好地分析和描述几何问题。
这些投影知识不仅在几何学中有重要应用,还在计算机图形学、建筑设计、工程制图等领域中发挥着重要作用。

点的投影知识点总结点的投影是指将一个点在一些方向上的投影。
在几何学中,点的投影是一种非常重要的概念,几乎应用到了所有的几何学中。
以下是点的投影的相关知识点的总结,包括定义、性质、计算方法以及应用等等。
1.投影的定义:投影可以定义为一个点在一些方向上的投影点,它是指点到一些方向上的垂直距离。
2.垂直投影和水平投影:垂直投影是指点到一些方向的垂直距离,而水平投影则是指点到一些方向的水平距离。
3.点到直线的投影:点到直线的投影是指从点到直线上的垂线段的长度。
计算点到直线的投影可以使用向量的方法或者坐标的方法。
4.在二维平面上的点到直线的投影的计算方法:-向量法:由直线的方向向量和点到直线的向量构成平行四边形,投影的长度等于平行四边形的高。
-坐标法:设直线的方程为Ax+By+C=0,点的坐标为(x,y),则点到直线的距离可以使用公式d=,Ax+By+C,/√(A^2+B^2)来计算。
5.在三维空间中的点到直线的投影的计算方法:-向量法:由直线的方向向量和点到直线的向量构成平行四边形,投影的长度等于平行四边形的高。
-坐标法:设直线的方程为Ax+By+Cz+D=0,点的坐标为(x,y,z),则点到直线的距离可以使用公式d=,Ax+By+Cz+D,/√(A^2+B^2+C^2)来计算。
6.点到平面的投影:点到平面的投影是指从点到平面上的垂线段的长度。
计算点到平面的投影可以使用向量的方法或者坐标的方法。
7.在三维空间中的点到平面的投影的计算方法:-向量法:由平面的法向量和点到平面的向量构成平行四边形,投影的长度等于平行四边形的高。
-坐标法:设平面的方程为Ax+By+Cz+D=0,点的坐标为(x,y,z),则点到平面的距离可以使用公式d=,Ax+By+Cz+D,/√(A^2+B^2+C^2)来计算。
8.点到曲线的投影:点到曲线的投影是指从点到曲线上的垂线段的长度。
计算点到曲线的投影可以使用微积分的方法。
9.投影的性质:-投影是个标量,不是个向量。
大一工程制图点的投影知识点总结在工程制图中,点的投影是其中的基础概念之一。
了解和掌握点的投影知识对于工程制图的学习和实践都至关重要。
本文将对大一工程制图点的投影知识点进行总结,以帮助读者更好地理解和应用这一概念。
1. 点的投影概念点是一个没有大小和形状的基本图形元素,而点的投影是指将点在某个平面上的投影位置。
在工程制图中,常用的投影平面有垂直于水平面(俯视图,即平面图)和垂直于垂直面(正视图,即立体图)的两个投影面。
2. 点在水平投影面上的投影当点在水平投影面上进行投影时,我们可以直接按照点的位置在水平面上标注出其投影位置。
水平投影也称为俯视图,是制图中最常用的一种投影。
3. 点在垂直投影面上的投影当点在垂直投影面上进行投影时,我们需要根据点的先后顺序和距离来确定其在投影面上的位置。
在垂直投影中,我们通常使用正视图来表示点的投影位置。
4. 点在多个投影面上的投影在实际工程制图中,一个点可能需要在多个投影面上进行投影。
这时,我们可以根据不同的投影面,分别画出该点在每个投影面上的投影位置。
通过在不同的视图中观察和标注这些投影,可以更全面地了解和描述点的位置。
5. 点的投影位置变化当点的位置发生变化时,其在投影面上的投影位置也会随之改变。
在工程制图中,通过观察和分析点在不同投影面上的变化,可以推断出点在三维空间中的实际位置。
6. 投影线与真实线在点的投影中,我们通常使用投影线来表示点在投影面上的投影位置。
投影线是连接点和投影位置的直线,它只是点在投影面上的一种表达方式,并不代表真实的线段或距离。
因此,在进行点的投影时,需要区分投影线和真实线之间的关系。
7. 点的投影应用点的投影不仅仅是一个理论概念,还具有广泛的应用价值。
在工程制图和设计中,点的投影可以帮助我们准确地定位和描述一个点的位置,从而为后续的图形绘制和建模提供基础。
同时,通过观察点在不同投影面上的变化,还可以推断出其他图形的投影位置和形态。
总结:点的投影是工程制图中的基础概念,了解和掌握点的投影知识对于工程制图的学习和实践都至关重要。
投影的基本知识、点的投影我们知道,零件是由若干个点、线、面等几何元素围成的几何体,而点又是构成线、面的基本元素,因此,如果掌握点的投影特性,对于学习画、读三视图将有很大的帮助。
我们先复习回忆一下上堂课的内容:圆弧连接的要点?平面图形的作图步骤?点是构成各几何体的最基本的要素,那么,点在投影面上的投影是什么?怎样得到点的投影呢?其投影又有什么规律性呢?这节课我们就来探讨这些问题。
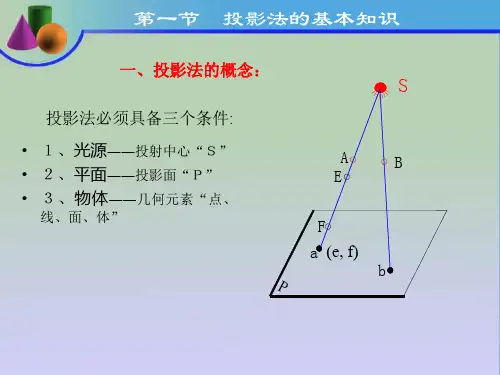
一、投影的基本知识物体在阳光等光线的照射下,就会在地面或墙壁上产生影子,这种现象称之为投影。
投射线通过物体,向选定的面投影,并在该面投影上得到图形的方法叫做投影法。
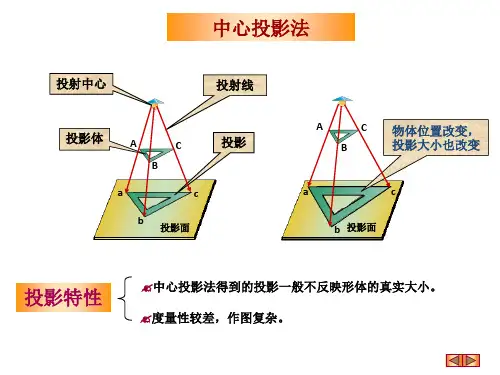
投影法分为中心投影法和平行投影法两大类:(一)中心投影法投射线汇交于一点的投影法叫做中心投影法。
(二)平行投影法投射线互相平行的投影法叫做平行投影法。
用时5分钟提问用时20分钟动画演示根据投射线与投射面是否垂直,平行投影法又分为两种:正投影法:投射线与投射面垂直的平行投影法。
斜投影法:投射线与投射面倾斜的平行投影法。
机械制图多采用正投影法绘制图样。
二、点的投影(一)点的投影及其规律点的投影仍然是一个点。
(二)点的三面投影1. 点的投影标记空间点用:A、B、C、D ……标记。
空间点在H面上的投影用:a、b、c、d ……标记;空间点在V面上的投影用:a′、b′、c′、d′……标记;空间点在W面上的投影用:a″、b″、c″、d″……标记。
2.点的投影规律点在三投影面体系中的投影规律:(1)连影垂直;(2)点的投影到投影轴的距离反映空间点到投影面的距离。
动画演示用时60分钟动画演示学员总结(三)点的坐标与投影之间的关系在三个相互垂直的投影面中,每两个投影面交于一个投影轴,形成了相互垂直的三个投影轴ox,oy和oz,三投影轴交于原点o。
这三个轴正可以作为一个空间坐标系的坐标轴。
空间点的位置可用三个坐标值x,y,z表示出来。
用时15分钟学员讨论、讲解这些坐标值反映在点的三投影中,就是点的投影到投影轴的距离。
投影法一、投影法的基本知识(从自然现象引深到投影理论,建立概念)投射线通过物体,向选定的面投射,并在该面上得到该物体图形的方法,称为投影法。
投影法的形成投影四要素: 投影中心、投影线、物体、投影面。
二、投影法的分类中心投影法:投影线相交于投影中心,如上图所示。
平行投影法:投影中心移至无限远时,投影线相互平行,平行投影法又分为正投影和斜投影,正投影的投影线垂直投影面,斜投影的投影线倾斜投影面。
斜投影法正投影法平行投影法机械图样中的图形主要采用正投影法绘制。
正投影图能正确表达物体的真实形状和大小,且作图方便,所以正投影是我们所要学习一种主要投影方法。
三、正投影的投影特性(对照立体图讲清投影特性,要求熟记结论)1.实形性:当直线、平面平行于投影面时,则在平行的投影面上的投影反映直线实长或平面的实形。
下图中平面 P、直线 AB 等。
2.积聚性:直线、平面和投影方向一致时,则它们在投影面上的投影分别积聚为点、直线、曲线。
下图中平面 Q、直线 AC 等。
3.类似性: 当直线、平面倾斜于投影面时,直线的投影仍为直线,平面的投影为平面图形的类似形。
下图中平面 R、直线 EF 等。
正投影法投影特性四、工程上常用的投影图1.透视图这种图是用中心投影法绘制,这种图符合人眼的视觉效果看起来形象逼真,。
但不能很明显地表达物体的真实形状和度量关系,同时作图很复杂,所以目前主要在建筑工程上作辅助性的图样使用。
2.轴测图这种图是用平行投影法绘制,有比较强立体感,一般都能看懂,但作图比较复杂,并且对复杂机件也难以表达清楚,故在工程上常作为辅助图样来使用。
3.多面正投影图多面正投影图能准确表达物体各部分之间的相互位置关系,且度量性好、作图简单,所以在工程上被广泛应用。
缺点是立体感差,要用多个图形才能表达清楚物体的形状特征。
4.标高投影图它是一种带有数字标记的单面正投影图。
它用正投影反映物体的长度和宽度,其高度用数字标注,标高投影图常用于表达地面的形状。
点、直线和平面>> 点>> 点在两投影面体系中的投影
1 点
1.1 点在两投影面体系中的投影
1.1.1 两投影面体系的建立
两投影面体系由互相垂直相交的两个投影面组成,如图1所示,其中一个为水平投影面(简称水平面),以H表示,另一个为正立投影面(简称正面),以V表示。
两投影面的交线称为投影轴,以OX表示。
水平投影面H与正立投影面V将空间分为四个部分,称为四个分角,即第一分角、第二分角、第三分角、第四分角。
(1) 投影如图2所示,空间点A处于第一分角,按正投影法将点A向正面和水平面投射,即由点A向正面作垂线,得垂足a′,则a′称为空间点A的正面投影;由点A向水平面作垂线,得垂足a ,则a称为空间点A的水平投影。
画出点A的正面投射线Aa′和水平投射线Aa所确定的平面Aaa′与V、H面的交线a′a x和aa x 。
图2 点在两投影面体系中的投影
(2) 注写规定空间点用大写字母表示,如A、B、C…;点的水平投影用相应的小写字母表示,如a、b、c…;点的正面投影用相应的小写字母加一撇表示,如a′、b′、c′…。
(3) 投影面展开为了把空间点A的两个投影表示在一个平面上,保持V面不动,将H 面的前半部分绕OX轴向下旋转90°、后半部分绕OX轴向上旋转90°与V面重合。
则得到点A的两面投影图。
(4) 擦去边界,得到点的两面投影图投影面可以看作是没有边界的平面,故符号V、H及投影面的边界线都不需画出。
1.1.3 点在两投影面体系中的投影规律
(a) (b)
图3 点在两投影面体系中的投影规律
(1) 一点的水平投影和正面投影的连线垂直于OX轴。
在图3(a)中,点A的正面投射线Aa′和水平投射线Aa所确定的平面Aaa′垂直于V 和H平面。
根据初等几何知识,若三个平面互相垂直,其交线必互相垂直,所以有aa x⊥a′a x、aa x⊥OX和a′a x⊥OX。
当a随H面旋转重合于V面时,aa x⊥OX的关系不变。
因此,在投影图上,aa′⊥OX。
(2) 一点的水平投影到OX轴的距离等于该点到V面的距离;其正面投影到OX轴的距离等于该点到H面的距离,即aa x=Aa′;a′a x=Aa。
在图3(a)中,因为Aaa x a′是矩形,所以aa x=Aa′; a′a x=Aa。
图4 分角内点的投影
如图7所示,三投影面体系是在V⊥H两投影面体系的基础上,增加一个与V、H投影面都垂直的侧立投影面W(简称侧面)组成的。
三个投影面互相垂直相交,其交线称为投影轴,V面和H面的交线为OX轴,H面和W面的交线为OY轴,V面和W面的交线为OZ轴。
OX、OY、OZ轴垂直相交于一点O,称为原点。
我们只在第一分角内研究各种问题。
图7 三投影面体系的建立
1.2.2 点的三面投影
(1) 投影如图8所示,设空间点A处于第一分角,按正投影法将点A分别向H、V、W面作垂线,其垂足即为点A的水平投影a、正面投影a′和侧面投影a″(点的侧面投影用相应的小写字母加两撇表示)。
(2) 投影面展开为了把空间点A的三面投影表示在一个平面上,保持V面不动,H面绕OX轴向下旋转90°与V面重合;W面绕OZ轴向右旋转90°与V面重合。
在展开过程中,OX轴和OZ轴位置不变,OY轴被“一分为二”,其中随H面向下旋转与OZ轴重合的一半,用OY H表示;随W面向右旋转与OX轴重合的一半,用OY W表示。
(3) 擦去边界,得到点的三面投影图擦去投影面边界线,则得到A点的三面投影图。
1.2.3 点的三面投影规律
如图9所示,三投影面体系可以看成由V⊥H、V⊥W两个两投影面体系组成。
根据点在两投影面体系中的投影规律,可知点在三投影面体系中的投影规律为:
1)点的正面投影和水平投影的连线垂直于OX轴,即a′a⊥OX;
2)点的正面投影和侧面投影的连线垂直于O Z轴,即a′a"⊥OZ;
3)点的水平投影到OX轴的距离和点的侧面投影到OZ轴的距离都等于该点到V面的距离,即aa x=a″a z=Aa′。
为了保持点的三面投影之间的关系,作图时应使aa′⊥OX、a′a″⊥OZ。
而aa x=a″a z可用图9(b)所示的以O为圆心,aa x或a″a z为半径的圆弧,或用图9(c)所示的过O点与水平成45°的辅助线来实现。
(a) (b)(c)
图9 点在三投影面体系中的投影规律
1.2.4 点的投影的直角坐标表示法
如图9,如果把三投影面体系看作笛卡儿直角坐标系,则H、V、W面为坐标面,OX、OY、OZ轴为坐标轴,O为坐标原点。
则点A到三个投影面的距离可以用直角坐标表示:点A到W面的距离Aa″=点A的x坐标值x A,且Aa″=aa y=a′a z=a x O;
点A到V面的距离Aa′=点A的y坐标值y A,且Aa′=aa x=a″a z=a y O;
点A到H面的距离Aa=点A的z坐标值z A,且Aa=a′a x=a″a y=a z O。
点A的位置可由其坐标(x A、y A、z A)唯一地确定。
其投影的坐标分别为:水平投影a(x A,y A,0);正面投影a′(x A,0,z A);侧面投影a″(0,y A,z A)。
因此,已知一点的三个坐标,就可作出该点的三面投影。
反之,已知一点的两面投影,也就等于已知该点的三个坐标,即可利用点的投影规律求出该点的第三面投影。
【例1】已知空间点A(12,8,16)、点B(8,12,0)、点C(0,0,10),求作它们的三面投影图。
【解】点A的三个坐标都为正值,故点A在第一分角内;点B的三个坐标中,z=0,
即B到H面的距离等于零,故点B在H面内;点C的三个坐标中,x=0,y=0,即C到W面和V面的距离都为零,故点C在OZ轴上。
如图10(a)所示,求点A的三面投影图的步骤如下:
(1) 画投影轴;
(2) 求a、a′
①由原点O向左沿OX轴量取12mm得a x;
②过a x作OX轴的垂线;
③在垂线上自a x向下(OY H方向)量取8mm得a;
④在垂线上自a x向上(OZ方向)量取16mm得a′;
(3) 求a″
①过a′作a′a z⊥OZ轴,交OZ轴于a z;
②过a作aa YH⊥OY H轴,交OY H轴于a YH,利用45°辅助线在OY W轴上得a YW;
③自a YW向上作OY W轴的垂线与aa z的延长线交于a″。
用同样的方法可作出B点的三面投影图如图10(b)所示,C点的三面投影图如图10(c)所示。
(a) (b)(c)
图10 由点的坐标作点的三面投影图
【例2】如图11(a)所示,已知点A的正面投影a′和侧面a″,求作该点的水平投影a。
【解】作图步骤如图11(b)所示:
①自a′向下作OX轴的垂线;
②自a″向下作OY W轴的垂线与45°辅助线交于一点,并由该交点作OY H轴的垂线,与过a′垂直于OX轴的直线交于a,a即为A点的水平投影。
(a) (b)
图11 由点的两面投影求其第三面投影
1.3 两点的相对位置
1.3.1 两点相对位置的确定
两点的相对位置是指以两点中的一点为基准,另一点相对该点的左右、前后和上下的位置。
点的位置由点的坐标确定,两点的相对位置则由两个点的坐标差确定。
如图12(a)所示,空间有两个点A(x A,y A,z A)、B(x B,y B,z B)。
若以B点为基准,则两点的坐标差为Δx AB=x A-x B、Δy AB=y A-y B、Δz AB=z A-z B。
x坐标差确定两点的左右位置,y坐标差确定两点的前后位置,z坐标差确定两点的上下位置。
三个坐标差均为正值,则点A在点B的左方、前方、上方。
从图12(b)看出,三个坐标差可以准确地反映在两点的投影图中。
1.3.2 重影点
当两点位于某一投影面的同一条投射线上时,这两点在该投影面上的投影重合,称这两点为对该投影面的重影点。
显然,两点在某一投影面上的投影重合时,它们必有两对相等的坐标。
如图13(a),A、B两点位于V面的同一条投射线上,它们的正面投影a′、b′重合,称A、B两点为对V面的重影点,这两点的x、z坐标分别相等,y坐标不等。
同理,C、D两点位于H面的同一条投射线上,它们的水平投影c、d重合,称C、D两点为对H面的重影点,它们的x、y坐标分别相等,z坐标不等。
(a) (b)
图13 重影点
由于重影点有一对坐标不相等,所以,在重影的投影中,坐标值大的点的投影会遮住坐标值小的点的投影,即坐标值大的点的投影可见,坐标值小的点的投影不可见。
在投影图中,对于重影的投影,在不可见点投影的字母两侧画上圆括号。
如图13(b),A、B两点为对V面的重影点,它们的正面投影重合,y A>y B,点A在点B的前方,a′可见,表示为a′;b′不可见,表示为(b′)。
C、D两点为对H面的重影点,它们的水平投影重合,z C >z D,点C在点D的上方,c可见,表示为c;d不可见,表示为(d)。