高等数值分析插值程序题Runge现象

插值MATLAB实现（牛顿差商插值误差龙格现象切比雪夫插值）插值是数值分析中的一种方法，通过已知数据点的函数值来估计函数在其他点的值。

MATLAB提供了多种方法来实现插值，包括牛顿差商插值、插值误差分析、龙格现象和切比雪夫插值。

下面将详细介绍这些方法的实现原理和MATLAB代码示例。

1.牛顿差商插值：牛顿差商插值是一种基于多项式插值的方法，其中差商是一个连续性的差分商。

该方法的优势在于可以快速计算多项式的系数。

以下是MATLAB代码示例：```matlabfunction [coeff] = newton_interpolation(x, y)n = length(x);F = zeros(n, n);F(:,1)=y';for j = 2:nfor i = j:nF(i,j)=(F(i,j-1)-F(i-1,j-1))/(x(i)-x(i-j+1));endendcoeff = F(n, :);end```该代码中，输入参数x和y分别表示已知数据点的x坐标和y坐标，返回值coeff表示插值多项式的系数。

2.插值误差分析：插值误差是指插值函数与原始函数之间的差异。

一般来说，通过增加插值节点的数量或使用更高次的插值多项式可以减小插值误差。

以下是MATLAB代码示例：```matlabfunction [error] = interpolation_error(x, y, x_eval)n = length(x);p = polyfit(x, y, n-1);y_eval = polyval(p, x_eval);f_eval = sin(pi*x_eval);error = abs(f_eval - y_eval);end```该代码中，输入参数x和y分别表示已知数据点的x坐标和y坐标，x_eval表示插值节点的x坐标，error表示插值误差。

3.龙格现象：龙格现象是插值多项式在等距插值节点上错误增长的现象。

1 / 21数值分析实验二：插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。

显然拉格朗日插值中使用的节点越多，插值多项式的次数就越高。

我们自然关心插值多项式的次数增加时， 是否也更加靠近被逼近的函数。

龙格（Runge ）给出一个例子是极著名并富有启发性的。

设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分，分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。

实验要求：(1) 选择不断增大的分点数目n=2, 3 …. ，画出原函数f(x)及插值多项式函数()n L x 在[-1，1]上的图像，比较并分析实验结果。

(2) 选择其他的函数，例如定义在区间[-5，5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。

(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式，比较其结果,试分析2 / 21原因。

1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上，根据拉格朗日插值多项式编写Matlab 脚本，其中把拉格朗日插值部分单独编写为f_lagrange.m 函数，方便调用。

1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20，画出原函数和拉格朗日插值函数的图像，如图1所示。

Matlab 脚本文件为Experiment2_1_1fx.m 。

可以看出，当n 较小时，拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x)，即插值效果越来越好。

数值分析实验报告（02）一、实验目的通过上机绘制Runge 函数图像，理解高次插值的病态性质。

二、实验内容在区间[-1,1]上分别取n=10,n=20用两组等距节点对龙格(Runge)函数21()125f x x =+作多项式插值，对每个n 值分别画出()f x 和插值函数的图形。

三、编程思路（相关背景知识、算法步骤、流程图、伪代码）四、程序代码（Matlab 或C 语言的程序代码）function yt=Untitled8(x,y,xt)%UNTITLED5 ´Ë´¦ÏÔʾÓйش˺¯ÊýµÄÕªÒª% ´Ë´¦ÏÔʾÏêϸ˵Ã÷n=length(x);ny=length(y);if n~=nyerror('²åÖµ½ÚµãxÓ뺯ÊýÖµy²»Ò»ÖÂ');endm=length(xt);yt=zeros(1,m);for k=1:nlk=ones(1,m);for j=1:nif j~=klk=lk.*(xt-x(j))/(x(k)-x(j));endend ;yt=yt+y(k)*lk;endn=input('n=');x=linspace(-1,1,n);y=1./(1+25.*x.^2);xf=linspace(-1,1,100);yf=1./(1+25.*xf.^2)xl=xf;yl=Untitled8(x,y,xf);plot(xf,yf,'-b',xl,yl,'-r')五、数值结果及分析（数值运行结果及对结果的分析）当n=10时当n=20六、实验体会（计算中出现的问题，解决方法，实验体会）出现符号错误，代码函数变量不明重新输入，查询错误，找到并改正编码需要认真仔细，一定要头脑清晰，避免出现一些低级错误。

1. 对Runge 函数22511)(x x R +=用在区间[-1, 1]下列条件作插值逼近，并和)(x R 的图像进行比较。

（1） 用等距节点ih x i +-=1，h=0.2, 绘出它的10次Newton 插值多项式的图像。

（2） 用节点)2212cos(1π++-=i x i (i=0,1,…,10)，绘出它的10次Newton 插值多项式的图像。

（3） 用等距节点ih x i +-=1，h=0.2, 绘出它的分段线性插值多项式的图像。

（4） 用等距节点ih x i +-=1，h=0.2, 绘出它的三次自然样条线性插值多项式的图像。

解：Newton 插值曲线与原曲线比较x 轴y 轴当x 在中间取值范围时，Newton 插值曲线与原曲线比较接近，但是当x 在两端时，Newton 插值曲线与原曲线相差越来越大，出现了Runge 现象。

插值余项∏=-=ni in n x x x x x x f x R 010)(],,,,[)( .由插值多项式的唯一性知)()(x N x L n n =，因此，牛顿插值与拉格朗日插值有相同的余项表达式，即∏∏==+∈-=-+=-=ni i n ni i n n n b a x x x x x f x x n f x N x f x R 000)1(],[),(],,,[)()!1()()()()(ξξ 由此有)!1()(],,,[)1(0+=+n f x x x f n n ξ .牛顿前插公式为002000!)1()1(!2)1()(f n n t t t f t t f t f th x N nn ∆+--++∆-+∆+=+ .其余项为),(),()!1()()1()()()(010n n n n x x f h n n t t t th x N x f x R ∈+--=+-=+ξξ牛顿后插公式为n nn n n n n f n n t t t f t t f t f th x N ∇-++++∇++∇+=+!)1()1(!2)1()(2 . 其余项为),(),()!1()()1()()()(0)1(1n n n n n n x x f h n n t t t th x N x f x R ∈+++=+-=++ξξLagrange 插值曲线与原曲线比较x 轴y 轴在这里由于x 不是等距节点，Lagrange 插值曲线与原曲线比较接近，没有出现Runge 现象。

⾼等数值分析插值程序题Runge现象插值程序题1.对Runge函数RR(xx)=1/(1+25xx2)在区间[-1,1]做下列插值逼近，并和RR(xx)的图像进⾏⽐较，并对结果进⾏分析。

（1）等距节点xx ii=?1+ii?,?=0.1,0≤?≤20,20次netown插值多项式图像；（2）节点xx ii=cos?2ii+142ππ?,(i=0,1,2,…,20),20次Lagrange插值多项式的图像；（3）等距节点xx ii=?1+ii?,?=0.1,0≤?≤20,20次分段线性插值函数图像；（4）等距节点xx ii=? 1+ii?,?=0.1,0≤?≤20,20次三次样条插值函数的图像。

解：（1）20次等距节点netown插值多项式和R(xx)的图像⽐较图如下所⽰（求值点之间的间隔为0.0001，以下相同）：从图像可以看出，在插值区间中部netown插值多项式与原Runge函数符合得较好；但在插值区间的两端两者的差别很⼤（netown在区间[-1,-0.9]的最⼩值为-59.7819），此时的插值余项不满⾜要求，因此⽤等距20次netown插值多项式来对Runge 函数在区间[-1,1]做插值逼近并不合适，会出现明显的Runge现象。

（2）20次⾮等距节点Lagrange插值多项式（切⽐雪夫多项式零点插值）和R(xx)的图像⽐较图如上所⽰。

此时插值的节点并不等距，插值节点两边密，中间疏，虽然此时Lagrange插值多项式也是20次，但相⽐等距netown插值，⾮等距Lagrange插值曲线与原函数吻合得很好，没有出现明显的Runge现象，两端⽐较密的插值节点较好地抑制了Runge现象。

为了⽐较节点选取对⾼次插值结果的影响，⽤20次等距Lagrange插值也原函数在区间[-1,1]进⾏了插值，其与原函数图像⽐较如下：其图像与（1）中netown插值⼏乎⼀样，因此对⾼次插值多项式，插值时适当的选取插值节点，能有效的抑制Runge现象。

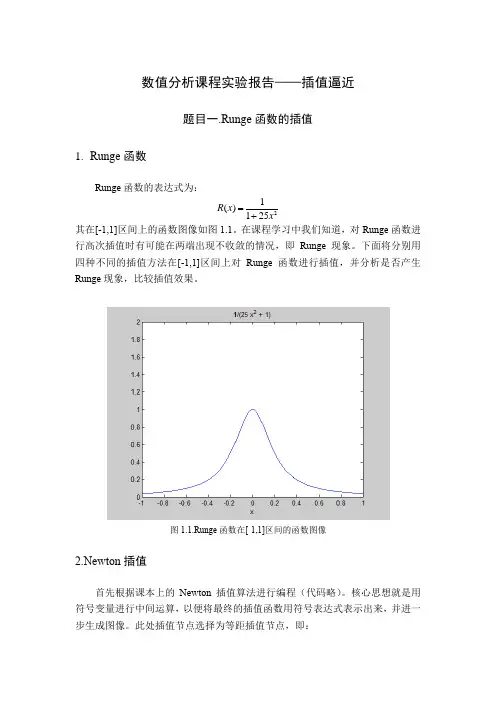
数值分析课程实验报告——插值逼近题目一.Runge 函数的插值1. Runge 函数Runge 函数的表达式为：21()125R x x =+ 其在[-1,1]区间上的函数图像如图1.1。

在课程学习中我们知道，对Runge 函数进行高次插值时有可能在两端出现不收敛的情况，即Runge 现象。

下面将分别用四种不同的插值方法在[-1,1]区间上对Runge 函数进行插值，并分析是否产生Runge 现象，比较插值效果。

图1.1.Runge 函数在[-1,1]区间的函数图像2.Newton 插值首先根据课本上的Newton 插值算法进行编程（代码略）。

核心思想就是用符号变量进行中间运算，以便将最终的插值函数用符号表达式表示出来，并进一步生成图像。

此处插值节点选择为等距插值节点，即：0.1(0,1,2,,)i x ih i =-+= (20)其中h=0.1。

插值曲线与原曲线的对比如图1.2（蓝色为原曲线，红色为插值曲线）。

从图中看出，在区间中部，二者吻合较好；但在区间两端二者则产生了明显偏差，甚至可以达到一个非常大的数值（e20量级）。

因此，在等距节点的20次Newton 插值下，产生了明显的Runge 现象。

图1.2.Newton 插值曲线与原曲线对比3. Lagrange 插值此处同样是根据Lagrange 插值的具体算法进行编程。

但插值节点不再是等距分布，而是如下形式：21cos()(0,1,2,,)42i i x i π+==…20 插值曲线与原曲线的对比如图1.3（蓝色为原曲线，红色为插值曲线）。

从图中看出，插值曲线与原曲线吻合的很好，没有产生明显的Runge 现象。

对比产生了明显Runge 现象的20次Newton 插值，Lagrange 插值的最高次数虽然也是20，但由于此处的插值节点不是等距分布的（事实上，此处采用的插值节点正是Chebyshev 多项式的零点），而是中间疏两边密，因此两侧较密的节点很好地抑制了Runge 现象。

实验三:Runge现象的产生和克服程序1：lagrange多项式插值syms f x p dp lx L;f=1/(1+25*x^2);N=input('请输入插值节点数N='); xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);syms x;p=p*(x-xx(i));enddp=diff(p);for j=1:(N+1)x=xx(j);k=eval(dp);syms x;lx=p/((x-xx(j))*k);L=L+lx*ff(j);endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa)x=aa(i);S(i)=eval(L);fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1])hold onezplot(L,[-1,1])hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off程序2：分段线性插值syms f x p lx;f=1/(1+25*x^2);N=input('请输入插值节点数N='); xx=-1:2/N:1;p=1; L=0; ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);endsyms xfor i=1:Nfor j=1:(N+1)if j==ilx(i,j)=(x-xx(i+1))/(xx(i)-xx(i+1));else if j==i+1lx(i,j)=(x-xx(i))/(xx(i+1)-xx(i));elselx(i,j)=0;endendendendp=lx*ff';aa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa)x=aa(i);for j=1:N+1if x<xx(j)breakendendS(i)=eval(p(j-1));fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1])hold onxxx=(-1:0.01:1);for i=1:length(xxx)x=xxx(i);for j=1:N+1if x<xx(j)breakendendSS(i)=eval(p(j-1));endplot(xxx,SS,'r')hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off程序3：三转角插值法syms f x df s s1 s2 s3 s4;f=1/(1+25*x^2);df=diff(f);N=input('请输入插值节点数N=');h=2/N;xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);dff(i)=eval(df);endsyms xfor i=1:Ns1=(x-xx(i+1))^2*(h+2*(x-xx(i)))*ff(i)/h^3; s2=(x-xx(i))^3*(h+2*(xx(i+1)-x))*ff(i+1)/h^ 3;s3=(x-xx(i+1))^2*(x-xx(i))*dff(i)/h^2; s4=(x-xx(i))^2*(x-xx(i+1))*dff(i+1)/h^2;s(i)=s1+s2+s3+s4;endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];for i=1:length(aa)x=aa(i);for j=1:N+1if x<xx(j)breakendendS(i)=eval(s(j-1));fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;end e=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e)ezplot(f,[-1,1])hold onxxx=(-1:0.01:1);for i=1:length(xxx)x=xxx(i);for j=1:N+1if x<xx(j)breakendendSS(i)=eval(s(j-1));endplot(xxx,SS,'r')hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off程序4：三弯矩插值法：syms f x ddf s;f=1/(1+25*x^2);ddf=diff(diff(f));N=input('请输入插值节点数N=');h=2/N;xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);ddff(i)=eval(ddf);endsyms xfor i=1:NA=(ff(i+1)-ff(i))/h-h*(ddff(i+1)-ddff(i))/6;B=ff(i)-h^2*ddff(i)/6;s(i)=(xx(i+1)-x)^3*ddff(i)/(6*h)+(x-xx(i))^3 *ddff(i+1)/(6*h)+A*(x-xx(i))+B;endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];for i=1:length(aa)x=aa(i);for j=1:N+1if x<xx(j)breakendendS(i)=eval(s(j-1));fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1])hold onxxx=(-1:0.01:1); for i=1:length(xxx)x=xxx(i);for j=1:N+1if x<xx(j)breakendendSS(i)=eval(s(j-1)); endplot(xxx,SS,'r')hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off图1：观察Runge现象图3：三转角插值：。