4.5电导率、迁移率、霍耳效应

霍尔效应实验报告霍尔效应实验报告1实验内容:1.保持不变，使Im从0.50到4.50变化测量VH.可以通过改变I和磁场B的方向消除负效应。

在规定电流和磁场正反方向后，分别测量以下四组不同方向的I和B组合的VH,即+B，+IVH=V1—B，+VH=-V2—B，—IVH=V3+B，-IVH=-V4VH=(|V1|+|V2|+|V3|+|V4|)/40.501.601.003.201.504.792.006.902.507.983.009.553.5011.174.0012.734.5014.34画出线形拟合直线图：ParameterValueError------------------------------------------------------------A0.115560.13364B3.165330.0475------------------------------------------------------------RDNP------------------------------------------------------------0.999210.183959<0.00012.保持I=4.5mA,测量Im—Vh关系VH=(|V1|+|V2|+|V3|+|V4|)/40.0501.600.1003.200.1504.790.2006.900.2507.980.3009.550.35011.060.40012.690.45014.31ParameterValueError------------------------------------------------------------A0.133890.13855B31.50.49241------------------------------------------------------------RDNP------------------------------------------------------------0.999150.190719<0.0001根本满足线性要求。

第四章半导体的导电性本章主要内容载流子在外加电场作用下的漂移运动半导体的迁移率、电导率和电阻率随温度和杂质浓度的变化规律迁移率的本质-----散射4.1 载流子的漂移运动迁移率1、欧姆定律对于金属，电流I = V(电压）/R（电阻）V-I关系是直线对于半导体，流过不同截面的电流强度不一定相同，“即电流分布不均匀，而欧姆定律不能说明材料内部各处电流的分布情况。

电流密度：通过垂直于电流方向的单位面积的电流J = ∆I/∆S单位：A/cm2或A/m2欧姆定律微分形式：上式把通过导体中某一点的电流密度和该处的电导率及电场强度直接联系了起来。

S故: 半导体导电= 电子导电J = Jn + Jp = (nqu平均自由程：载流子在连续两次散射间自由运动的平均路程平均自由时间：载流子通过平均自由程所需的平均时间τ电场：载流子加速---定向运动；散射：载流子运动方向改变---杂乱无章，各个方向；半导体的主要散射机构：离化杂质散射晶格散射中性杂质散射位错散射(P为散射几率)起因：常温下，浅施主带正电• 双曲线，电离杂质处于一个焦点 • 速度小，作用时间长，偏离角θ大，τ小 • 弹性散射，不改变入射电子能量，只改变运动方向 τ ∝ T3/2/NI 杂质浓度（2）、晶格散射 晶格原子在其平衡位置附近不断进行热振动，且各个 原子的振动不是孤立的。

分析表明：晶格中原子的振动都 是由若干不同的基本波动按波的叠加原理组合而成，这些 基本波动称为格波。

q代表格波波矢， q 的方向即波的传播方向晶格散射：载流子在运动过程中遭受振动的晶格原子的散射， 失去在电场中获得的能量，失去动量。

在能带具有单一极值的半导体中 起主要散射作用的是长波。

即波 长比原子间距大很多倍的格波。

电子热运动速度~105m/s 电子波波长约10-8m 根据动量守恒要求，声子波长 范围应在同一量级，即10-8m,而 晶体中原子间距为10-10m，因而 起主要散射作用的是长波。

【⼤学物理实验】霍尔效应与应⽤讲义霍尔效应与应⽤1879年，年仅24岁的霍尔在导师罗兰教授的⽀持下，设计了⼀个根据运动载流⼦在外磁场中的偏转来确定在导体或半导体中占主导地位的载流⼦类型的实验，霍尔的发现在当时震动了科学界，这种效应被称为霍尔效应。

通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流⼦浓度、载流⼦迁移率等主要参数。

通过测量霍尔系数和电导率随温度变化的关系，还可以求出半导体材科的杂质电离能和材料的禁带宽度。

如今常规霍尔效应不但是测定半导体材料电学参数的主要⼿段，利⽤该效应制成的霍尔器件已⼴泛⽤于⾮电量的电测量、⾃动控制和信息处理等各个研究领域。

该实验要求学⽣了解霍尔效应的基本原理、霍尔元件的基本结构，测试霍尔元件特性的⽅法，并对测量结果给出正确分析和结论。

⿎励学⽣运⽤霍尔效应的基本原理和霍尔元件的特性，设计⼀些测量磁场，或各种⾮磁性和⾮电性物理量的测量的实验⽅案，例如：磁场分布、位置、位移、⾓度、⾓速度等。

让学⽣更好的运⽤霍尔效应来解决⼀些实际问题。

⼀、预备问题1．霍尔效应在基础研究和应⽤研究⽅⾯有什么价值？2．如何利⽤实验室提供的仪器测量半导体材料的霍尔系数？3．怎样判断霍尔元件载流⼦的类型，计算载流⼦的浓度和迁移速率？4．伴随霍尔效应有那些副效应？如何消除？5．如何利⽤霍尔效应和元件测量磁场？6．如何利⽤霍尔元件进⾏⾮电磁的物理量的测量？7．若磁场的法线不恰好与霍尔元件⽚的法线⼀致，对测量结果会有何影响？如何⽤实验的⽅法判断B与元件法线是否⼀致？8．能否⽤霍尔元件⽚测量交变磁场？⼆、引⾔霍尔效应发现⼀百多年来，在基础和应⽤研究范围不断扩展壮⼤，反常霍尔效应、整数霍尔效应、分数霍尔效应、⾃旋霍尔效应和轨道霍尔效应等相继被发现，并构成了⼀个庞⼤的霍尔效应家族。

1985年克利青、多尔达和派波尔因发现整数量⼦霍尔效应，荣获诺贝尔奖；1998年诺贝尔物学理奖授予苏克林、施特默和崔琦，以表彰他们发现了分数量⼦霍尔效应。

实验三霍尔效应法测量半导体的载流子浓度、电导率和迁移率一、实验目的1．了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识。

2．学习用“对称测量法”消除副效应的影响，测量并绘制试样的 VH－IS 和VH－IM 曲线。

3．确定试样的导电类型、载流子浓度以及迁移率。

二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。

当带电粒子（电子或空穴）被约束在固体材料中，这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积，从而形成附加的横向电场，即霍尔电场。

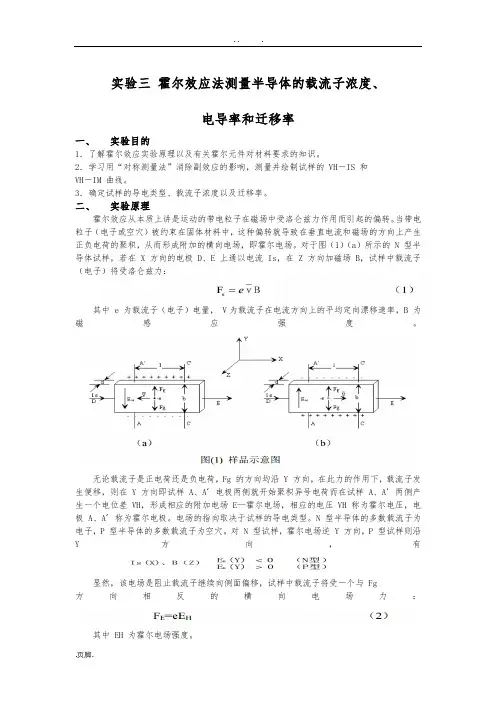
对于图（1）（a）所示的 N 型半导体试样，若在 X 方向的电极 D、E 上通以电流 Is，在 Z 方向加磁场 B，试样中载流子（电子）将受洛仑兹力：其中 e 为载流子（电子）电量， V为载流子在电流方向上的平均定向漂移速率，B 为磁感应强度。

无论载流子是正电荷还是负电荷，Fg 的方向均沿 Y 方向，在此力的作用下，载流子发生便移，则在 Y 方向即试样 A、A´电极两侧就开始聚积异号电荷而在试样 A、A´两侧产生一个电位差 VH，形成相应的附加电场 E—霍尔电场，相应的电压 VH 称为霍尔电压，电极 A、A´称为霍尔电极。

电场的指向取决于试样的导电类型。

N 型半导体的多数载流子为电子，P 型半导体的多数载流子为空穴。

对 N 型试样，霍尔电场逆 Y 方向，P 型试样则沿Y 方向，有显然，该电场是阻止载流子继续向侧面偏移，试样中载流子将受一个与 Fg方向相反的横向电场力：其中 EH 为霍尔电场强度。

FE 随电荷积累增多而增大，当达到稳恒状态时，两个力平衡，即载流子所受的横向电场力 e EH 与洛仑兹力eVB 相等，样品两侧电荷的积累就达到平衡，故有设试样的宽度为 b ，厚度为 d ，载流子浓度为 n ，则电流强度V Is 与的 关系为由（3）、（4）两式可得即霍尔电压 VH （A 、A ´电极之间的电压）与 IsB 乘积成正比与试样厚度 d 成反比。

霍尔效应电导率计算公式1. 什么是霍尔效应电导率计算公式？霍尔效应电导率计算公式是一种利用霍尔效应原理，计算半导体材料电导率的公式。

霍尔效应是指半导体中电子在电场作用下，受洛伦兹力偏转，从而在垂直于电场方向的外加磁场中产生电势差的现象。

电势差与电场强度、磁场强度及半导体类型有关，因此可以用来计算半导体的电导率。

2. 霍尔效应电导率计算公式具体是怎样的？霍尔效应电导率计算公式为：σ = R_h / R_xx * nq其中，σ为半导体材料的电导率；R_h为霍尔系数；R_xx为半导体材料在垂直于电场方向时的电阻率；n为载流子浓度；q为电子电荷。

3. 霍尔系数和电导率的关系是什么？霍尔系数与电导率是密切相关的。

霍尔系数可以用来计算半导体材料的电导率，其公式为：R_h = 1 / nq * (E_y / I_xB_z)其中，R_h为霍尔系数；n为载流子浓度；q为电子电荷；E_y为垂直于电场方向的霍尔电场强度；I_x为电流强度；B_z为垂直于半导体表面的磁场强度。

可以看出，电导率计算公式中的霍尔系数和载流子浓度都是影响半导体电导率的重要因素。

4. 霍尔效应电导率计算公式的应用领域是什么？霍尔效应电导率计算公式在半导体材料的研究中被广泛应用。

例如，在半导体器件的设计和制备过程中，通过测量霍尔系数和电阻率等参数，可以确定半导体材料的电导率，为器件的改良、优化和性能评价提供参考。

此外，利用霍尔效应原理，还可以研究半导体的电子结构、载流子性质等方面的问题，为半导体物理学和材料科学的研究提供有力支持。

综上所述，霍尔效应电导率计算公式是一项重要的物理学技术，具有广泛的应用前景和研究价值。

计算霍尔系数rh、载流子浓度n、电导率σ及迁移率下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!计算霍尔系数、载流子浓度、电导率及迁移率的详细步骤在固体材料物理学和电子工程中，霍尔效应被广泛应用于测量材料的电学特性，特别是载流子浓度、电导率和迁移率等重要参数。

实验三-霍尔效应法测量半导体的载流子浓度、-电导率和迁移实验三霍尔效应法测量半导体的载流子浓度、电导率和迁移率一、实验目的1．了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识。

2．学习用“对称测量法”消除副效应的影响，测量并绘制试样的VH－IS 和VH－IM 曲线。

3．确定试样的导电类型、载流子浓度以及迁移率。

二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。

当带电粒子（电子或空穴）被约束在固体材料中，这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积，从而形成附加的横向电场，即霍尔电场。

对于图（1）（a）所示的N 型半导体试样，若在X 方向的电极D、E 上通以电流Is，在Z 方向加磁场B，试样中载流子（电子）将受洛仑兹力：其中e 为载流子（电子）电量，V为载流子在电流方向上的平均定向漂移速率，B 为磁感应强度。

无论载流子是正电荷还是负电荷，Fg 的方向均沿Y 方向，在此力的作用下，载流子发生便移，则在Y 方向即试样A、A´电极两侧就开始聚积异号电荷而在试样A、A´两侧产生一个电位差VH，形成相应的附加电场E—霍尔电场，相应的电压VH 称为霍尔电压，电极A、A´称为霍尔电极。

电场的指向取决于试样的导电类型。

N 型半导体的多数载流子为电子，P 型半导体的多数载流子为空穴。

对N 型试样，霍尔电场逆Y 方向，P 型试样则沿Y 方向，有显然，该电场是阻止载流子继续向侧面偏移，试样中载流子将受一个与Fg方向相反的横向电场力：其中EH 为霍尔电场强度。

FE 随电荷积累增多而增大，当达到稳恒状态时，两个力平衡，即载流子所受的横向电场力e EH 与洛仑兹力eVB相等，样品两侧电荷的积累就达到平衡，故有设试样的宽度为b，厚度为d，载流子浓度为n，则电流强度V Is 与的关系为由（3）、（4）两式可得即霍尔电压VH（A、A´电极之间的电压）与IsB 乘积成正比与试样厚度d成反比。

霍尔效应测载流子迁移率霍尔效应是一个应用广泛的物理现象，可以通过它来测量固体材料中载流子的性质与数量。

在这个过程中，我们需要测量的一个重要参数就是载流子迁移率。

载流子迁移率是一个描述载流子流动性能的物理量，它可以帮助我们了解材料的导电性质以及材料中载流子的运动情况。

本文将简要介绍霍尔效应的原理和测载流子迁移率的方法。

一、霍尔效应的原理霍尔效应是指一种在一定条件下发生的运动电场效应。

当一个导电样品置于外电场中时，电子和空穴会被电场吸引或排斥而运动，从而在样品内部产生一个横向电场垂直于电场方向，这个横向电场就是霍尔电场。

霍尔电场产生的本质是由于电子因为洛伦兹力的作用而在横向方向上移动，从而在该方向上产生一个电场。

这个横向电场会使电子在该方向上运动，从而产生一些横向的电流，这就是霍尔电流。

通过测量霍尔电流和外部电场强度的关系，我们就可以得到样品电子迁移率的信息，从而了解样品内部的载流子性质。

二、测量载流子迁移率的方法测量载流子迁移率的方法一般有两种：霍尔常数法和四探针法。

1、霍尔常数法霍尔常数法通过测量载流子在横向电场中的漂移速率，从而计算出载流子迁移率。

方法如下：（1）将待测样品置于外部磁场中，使其处于霍尔平衡状态。

（2）施加一个横向电场E，用电表测量样品中薄板上的霍尔电压UH。

（3）测量霍尔电流IH，这个电流跟样品中的迁移率有关。

（4）通过测量霍尔电流大小和霍尔电压大小之间的比值得到霍尔常数RH。

（5）根据横向电场和磁场的大小，以及样品的几何形状，可以计算出样品中的载流子迁移率μ。

2、四探针法四探针法是另一种测量载流子迁移率的方法，它通过四个探针来测量材料的电导率和电阻率。

四探针法的原理是利用一对电极施加电压，再用其它两个电极测量样品的电压，然后计算样品中的电阻率和电导率。

这种方法可以准确地测量载流子迁移率，并且对样品的几何形状不敏感。

大学物理实验报告【实验名称】霍尔效应【实验目的】1．了解霍尔效应实验原理以及有关霍尔器件对材料要求的知识。

2．学习用“对称测量法”消除付效应的影响，测量试样的VH—IS；和VH—IM 曲线。

3．确定试样的导电类型、载流子浓度以及迁移率。

【实验仪器】霍尔效应实验仪【实验原理】霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。

当带电粒子(电子或空穴)被约束在固体材料中，这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积，从而形成附加的横向电场，即霍尔电场。

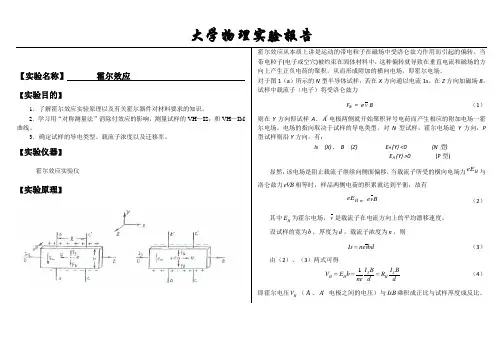
对于图1（a）所示的N型半导体试样，若在X方向通以电流1s，在Z方向加磁场B，试样中载流子（电子）将受洛仑兹力F B= e v B （1）则在Y方向即试样A、A'电极两侧就开始聚积异号电荷而产生相应的附加电场一霍尔电场。

电场的指向取决于试样的导电类型。

对N型试样，霍尔电场逆Y方向，P 型试样则沿Y方向，有：Is (X)、B (Z) E H (Y) <0 (N型)E H (Y) >0 (P型)显然，该电场是阻止载流子继续向侧面偏移，当载流子所受的横向电场力HeE与洛仑兹力eVB相等时，样品两侧电荷的积累就达到平衡，故有HeE= B v e（2）其中HE为霍尔电场，v是载流子在电流方向上的平均漂移速度。

设试样的宽为b，厚度为d，载流子浓度为n，则bdvneIs=（3）由（2）、（3）两式可得dBIRdBInebEV SHSHH===1（4）即霍尔电压HV（A、A'电极之间的电压）与IsB乘积成正比与试样厚度成反比。

.) (mA IS)(1mvV)(2mvV)(3mvV)(4mvV)(44321mvVVVVVR-+-=BIS++...BIS-+...BIS+-...BIS--...1.00 4.09 4.02 4.02 4.11 0.041.50 6.15 6.03 6.06 6.18 0.062.00 8.21 8.3 8.04 8.20 0.0852.50 10.25 10.06 10.04 10.27 0.1053.00 12.33 12.05 12.05 12.29 0.1304.00 16.39 16.07 16.09 16.41 0.160)(mA IM)(1mvV)(2mvV)(3mvV)(4mvV)(44321mvVVVVVH-+-=BIS++...BIS-+...BIS+-...BIS--...0.300 4.18 4.02 3.95 4.18 0.0975 0.400 5.52 5.37 5.30 5.49 0.0850.500 6.84 6.68 6.67 6.84 0.08250.600 8.19 8.04 8.03 8.21 0.08250.700 9.55 9.04 9.38 9.55 0.1700.800 10.90 10.75 10.74 10.92 0.0825mvV1.167=σmmd5.0=mml3=mmb5=TAKGSB364.0/64.3==由公式ccmBIdVRSHH/0549.01036401105.004.0103848=⨯⨯⨯⨯=⨯=-由公式1719108.8106.10549.011--⨯=⨯⨯==eRnH由公式63.143105.051.167233=⨯⨯⨯⨯==-SVlISσσ西门子/米由公式89.763.1430549.0=⨯==σμHR.【小结与讨论】(1)了解了霍尔效应实验原理以及有关霍尔器件丢材料的要求的知识，了解到一些物理量比如说霍尔系数，迁移率，电导率霍尔灵敏度等(2)如何判别霍尔元件的载流子类型？讨论知道电流方向一定，载流子的受力方向就一定，载流子会在受力方向积累，然后观测其正负。

实验四霍尔效应法测量半导体的载流子浓度、电导率和迁移一、实验目的1．了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识。

2．学习用“对称测量法”消除副效应的影响，测量并绘制试样的VH－IS和VH－IM 曲线。

3．确定试样的导电类型、载流子浓度以及迁移率。

二、实验原理置于磁场中的半导体，如果电流方向与磁场垂直，则在垂直于电流和磁场的方向会产生一附加的横向电场，这个现象是霍普斯金大学研究生霍尔于1879年发现的，后被称为霍尔效应。

随着半导体物理学的迅速发展，霍尔系数和电导率的测量已成为研究半导体材料的主要方法之一。

通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流子浓度、载流子迁移率等主要参数。

若能测量霍尔系数和电导率随温度变化的关系，还可以求出半导体材料的杂质电离能和材料的禁带宽度。

如今，霍尔效应不但是测定半导体材料电学参数的主要手段，而且随着电子技术的发展，利用该效应制成的霍尔器件，由于结构简单、频率响应宽（高达10GHz）、寿命长、可靠性高等优点，已广泛用于非电量测量、自动控制和信息处理等方面。

在工业生产要求自动检测和控制的今天，作为敏感元件之一的霍尔器件，将有更广阔的应用前景。

了解这一富有实用性的实验，对日后的工作将有益处。

霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。

当带电粒子（电子或空穴）被约束在固体材料中，这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积，从而形成附加的横向电场，即霍尔电场。

对于图（1）（a）所示的N型半导体试样，若在X方向的电极D、E上通以电流Is，在Z方向加磁场B，试样中载流子（电子）将受洛仑兹力：（1）其中e为载流子（电子）电量，为载流子在电流方向上的平均定向漂移速率，B为磁感应强度。

（a）（b）图(1) 样品示意图无论载流子是正电荷还是负电荷，Fg的方向均沿Y方向，在此力的作用下，载流子发生便移，则在Y方向即试样A、A´电极两侧就开始聚积异号电荷而在试样A、A´两侧产生一个电位差VH，形成相应的附加电场E—霍尔电场，相应的电压VH称为霍尔电压，电极A、A´称为霍尔电极。

实验三霍尔效应法测量半导体的载流子浓度、电导率和迁移率一、实验目的1．了解霍尔效应实验原理以与有关霍尔元件对材料要求的知识。

2．学习用“对称测量法〞消除副效应的影响，测量并绘制试样的 VH－IS 和VH－IM 曲线。

3．确定试样的导电类型、载流子浓度以与迁移率。

二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。

当带电粒子〔电子或空穴〕被约束在固体材料中，这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积，从而形成附加的横向电场，即霍尔电场。

对于图〔1〕〔a〕所示的 N 型半导体试样，假如在 X 方向的电极 D、E 上通以电流 Is，在 Z 方向加磁场 B，试样中载流子〔电子〕将受洛仑兹力：其中 e 为载流子〔电子〕电量， V为载流子在电流方向上的平均定向漂移速率，B 为磁感应强度。

无论载流子是正电荷还是负电荷，Fg 的方向均沿 Y 方向，在此力的作用下，载流子发生便移，如此在 Y 方向即试样 A、A´电极两侧就开始聚积异号电荷而在试样 A、A´两侧产生一个电位差 VH，形成相应的附加电场 E—霍尔电场，相应的电压 VH 称为霍尔电压，电极 A、A´称为霍尔电极。

电场的指向取决于试样的导电类型。

N 型半导体的多数载流子为电子，P 型半导体的多数载流子为空穴。

对 N 型试样，霍尔电场逆 Y 方向，P 型试样如此沿Y 方向，有显然，该电场是阻止载流子继续向侧面偏移，试样中载流子将受一个与 Fg方向相反的横向电场力：其中 EH 为霍尔电场强度。

FE 随电荷积累增多而增大，当达到稳恒状态时，两个力平衡，即载流子所受的横向电场力 e EH 与洛仑兹力eVB相等，样品两侧电荷的积累就达到平衡，故有设试样的宽度为 b，厚度为 d，载流子浓度为 n，如此电流强度V Is 与的关系为由〔3〕、〔4〕两式可得即霍尔电压 VH〔A、A´电极之间的电压〕与 IsB 乘积成正比与试样厚度 d成反比。

1第四章载流子输运与过剩载流子现象Chapter 4 Carrier Transport and Excess Carrier PhenomenaPreviewIn this chapter, we will1. Describe the mechanism of carrier drift and drift current due to an applied electric field.2. Describe the mechanism of carrier diffusion and diffusion current due to a gradient in the carrier concentration.3. Describe the effects in a semiconductor when a nonuniform impurity concentration exists .4. Describe the generation and recombination processes of excess carriers in a semiconductor.5. Describe and analyze the Hall effect in a semiconductor material.2Outline4.1 Carrier Drift (漂移)4.2 Carrier Diffusion(扩散）4.3 Graded Impurity Distribution (缓变杂质分布的影响)4.4 Carrier Generation(产生) and Recombination (复合)4.5 The Hall Effect(霍尔效应)4.6 Summary3In Chapter 3, we have considered the semiconductor in thermal equilibrium and determined electron and hole concentrations in the conduction and valence bands , respectively.The net flow of electrons and holes in a semiconductor will generate currents.The process by which these charged particles move is called transport.The two transport mechanisms, drift and diffusion , will be analyzed in this chapter. We will also discuss the generation and recombination processes in a semiconductor material.44.1 载流子的漂移运动§4.1 Carrier DriftObjective: Describe the mechanism of carrier drift and drift current due to an applied electric field.1. Drift current densityWhen an electric field is applied to a semiconductor, it will produce a force on electrons and holes so that they will experience a net acceleration and net movement, provided there are available energy states in the conduction and valence bands .This net movement of charge due to an electric field is called drift . The net drift of charge will lead to a drift current .Drift Current Density52. Mobility （迁移率）EffectsThe mobility is an important parameter of the semiconductor since it describes how fast a particle will move due to an electric field. The unit of mobility is usually expressed in terms of cm 2/V·s. There are two collision or scattering mechanisms thatdominate in a semiconductor and affect the carrier mobility: phonon or lattice scattering , and ionized impurity scattering.63. Semiconductor Conductivity （电导率）and Resistivity(电阻率）4. Velocity Saturation(速度饱和）At low electric fields , there is a linear variation of velocity with electric field . At high electric fields , the drift velocity of electrons in silicon saturates at approximately 107cm/s at an electric field of approximately 30 kV/cm . The drift current density also saturates and becomes independent of the applied electric field.74.1.1 Drift Current Density (漂移电流密度）4.1.2 Mobility Effects (迁移率效应)4.1.3 Semiconductor Conductivity(电导率) and Resistivity (电阻率)4.1.4 Velocity Saturation (速度饱和效应)4.1.1 Drift Current Density9Generally speaking, for low electric fields , carries will gain an average velocity which is directly proportional to the electric field , namely μ——carrier mobility (载流子的迁移率), unit is cm 2/V·s 。

实验陈述之邯郸勺丸创作姓名:学号:系别:座号:实验题目:通过霍尔效应丈量磁场实验目的:通过实验丈量半导体资料的霍尔系数和电导率可以判断资料的导电类型、载流子浓度、载流子迁移率等主要参数实验内容:已知参数：；3.Linear Regression for Data3_V:Y = A + B * XParameter Value Error----------------------------------------------------------------------------------R SD N P-----------------------------------------------------------------------------------------------------4.n、σ和μ(1)确定样品的导电类型控制电流和磁场方向如图所示时，电压表读数为正.可知薄片S的上概况积累正电荷,下概况积累负电荷.再根据洛沦兹力的受力规则判断,载流子受力向下,再由下概况积累负电荷知,载流.所以导电类型为n型.(2)由1和2(3)(4)(5)求μ实验分析:本实验采取数字仪表控制,所以相当精确.思考题:(1)若磁场不恰好与霍尔元件的法线一致,对丈量结果会有何影响？如何用实验的方法判断B与法线方向是否一致？若磁场不恰好与霍尔元件的法线一致,则霍尔片通过电流时,载流子的偏转方向就会偏离法线方向,从而使测得的电位差不是真正的霍尔电位差,从而造成丈量的系统误差.朝两个方向偏转霍尔元件的方向，如果电位差都减小，说明B与法线方向一致。

(2)若霍尔元件片的几何尺寸为，即控制电流两端距离为6mm，而电压两端距离为4mm，问此霍尔元件能否丈量面积为的气隙的磁场？可以.因为此时两个霍尔片电极都在磁场中,所以载流子仍可以偏转、积累,发生电位差.(3)能否用霍尔元件片丈量交变磁场？可以.因为霍尔效应建立的时间极短,使用交流磁场时,所得的霍尔电压也是交变的,此时B和V应理解为有效值.。