统计公差分析方法概述

统计公差分析方法概述(2012-10-23 19:45:32)分类：公差设计统计六标准差统计公差分析方法概述一.引言公差设计问题可以分为两类：一类是公差分析(Tolerance Analysis ,又称正计算) ,即已知组成环的尺寸和公差,确定装配后需要保证的封闭环公差；另一类是公差分配(Tolerance Allocation ,又称反计算) ,即已知装配尺寸和公差,求解组成环的经济合理公差。

公差分析的方法有极值法和统计公差方法两类,根据分布特性进行封闭环和组成环公差的分析方法称为统计公差法.本文主要探讨统计公差法在单轴向(One Dimension)尺寸堆叠中的应用。

二.Worst Case Analysis极值法(Worst Case ,WC)，也叫最差分析法，即合成后的公差范围会包括到每个零件的最极端尺寸,无论每个零件的尺寸在其公差范围内如何变化,都会100% 落入合成后的公差范围内。

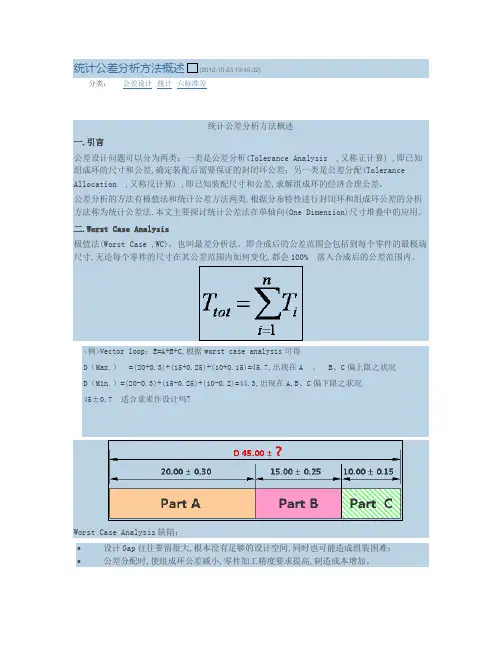
<例>Vector loop：E=A+B+C,根据worst case analysis可得D（Max.）=(20+0.3)+(15+0.25)+(10+0.15)=45.7,出现在A、B、C偏上限之状况D（Min.）=(20-0.3)+(15-0.25)+(10-0.2)=44.3,出现在A,B、C偏下限之状况45±0.7适合拿来作设计吗?Worst Case Analysis缺陷：•设计Gap往往要留很大,根本没有足够的设计空间,同时也可能造成组装困难；•公差分配时,使组成环公差减小,零件加工精度要求提高,制造成本增加。

以上例Part A +Part B+ Part C，假设A、B、C三个部材,相对于公差规格都有3σ的制程能力水平，则每个部材的不良机率为1-0.9973=0.0027；在组装完毕后所有零件都有缺陷的机率为：0.0027^3=0.000000019683。

这表明几个或者多个零件在装配时,同一部件的各组成环,恰好都是接近极限尺寸的情况非常罕见。

生产现场S H O P S O L U T I O N S金属加工汽车工艺与材料 A T&M2009年第7期50机械装配过程中，在保证各组成零件适当功能的前提下，各组成零件所定义的、允许的几何和位置上的误差称为公差。

公差的大小不仅关系到制造和装配过程，还极大影响着产品的质量、功能、生产效率以及制造成本。

公差信息是产品信息库中的重要内容，公差模型就是为表示公差信息而建立的数学及物理模型，它是进行公差分析的理论基础。

公差分析或称偏差分析，即通过已知零部件的尺寸分布和公差，考虑偏差的累积和传播，以计算装配体的尺寸分布和装配公差的过程。

公差分析的目的在于判断零部件的公差分布是否满足装配功能要求，进而评价整个装配的可行性。

早期公差分析方法面向的是一维尺寸公差的分析与计算。

Bjorke 则将公差分析拓展到三维空间。

Wang 、C h a s e 、P a b o n 、H o f f m a n 、Lee 、Turner 、Tsai 、Salomons 、Varghese 、Connor 等许多学者也分别提出了各自的理论和方法开展公差分析的研究。

此后，人工智能、专家系统、神经网络、稳健性理论等工具被引入公差分析领域当中，并分别构建了数学模型以解决公差分析问题。

1 公差模型公差模型可分为零件层面的公差信息模型和装配层面的公差拓扑关系模型。

Shan 提出了完整公差模型的建模准则，即兼容性和可计算性准则。

兼容性准则是指公差模型满足产品设计过程的要求，符合ISO 和ASME 标准，能够完整表述所有类型的公差。

可计算性准则是指公差模型可实现与CAD 系统集成、支持过/欠约束、可提取隐含尺寸信息、可识别公差类型，以检查公差分配方案的可行性等。

目前已经提出了很多公差模型表示法，但每一种模型都是基于一些假设，且只部分满足了公差模型的建模准则，至今尚未出现统一的、公认的公差模型。

以下将对几种典型的公差模型加以介绍和评价。

统计公差分析方法概述一、引言公差设计问题可以分为两类:一类就是公差分析(Tolerance Analysis ,又称正计算) ,即已知组成环的尺寸与公差,确定装配后需要保证的封闭环公差;另一类就是公差分配(Tolerance Allocation ,又称反计算) ,即已知装配尺寸与公差,求解组成环的经济合理公差。

公差分析的方法有极值法与统计公差方法两类,根据分布特性进行封闭环与组成环公差的分析方法称为统计公差法、本文主要探讨统计公差法在单轴向(One Dimension)尺寸堆叠中的应用。

二、Worst Case Analysis极值法(Worst Case ,WC),也叫最差分析法,即合成后的公差范围会包括到每个零件的最极端尺寸,无论每个零件的尺寸在其公差范围内如何变化,都会100% 落入合成后的公差范围内。

<例>Vector loop:E=A+B+C,根据worst case analysis可得D(Max、)=(20+0、3)+(15+0、25)+(10+0、15)=45、7,出现在A、B、C偏上限之状况D(Min、)=(20-0、3)+(15-0、25)+(10-0、2)=44、3,出现在A,B、C偏下限之状况45±0、7适合拿来作设计不?Worst Case Analysis缺陷:•设计Gap往往要留很大,根本没有足够的设计空间,同时也可能造成组装困难;•公差分配时,使组成环公差减小,零件加工精度要求提高,制造成本增加。

以上例Part A +Part B+ Part C,假设A、B、C三个部材,相对于公差规格都有3σ的制程能力水平,则每个部材的不良机率为1-0、9973=0、0027;在组装完毕后所有零件都有缺陷的机率为:0、0027^3=0、3。

这表明几个或者多个零件在装配时,同一部件的各组成环,恰好都就是接近极限尺寸的情况非常罕见。

三、统计公差分析法•由制造观点来瞧,零件尺寸之误差来自于制程之变异,此变异往往呈现统计分布的型态,因此设计的公差规格常被视为统计型态。

公差数据处理与分析技巧公差数据处理与分析技巧公差是指在制造过程中，由于各种原因造成的产品尺寸、形状、位置等方面的偏差。

准确地处理和分析公差数据对于确保产品质量和满足设计要求至关重要。

下面将介绍一些公差数据处理与分析的技巧。

首先，对于公差数据的处理，我们需要进行数据的收集和整理。

在制造过程中，我们需要收集每个产品的测量数据，包括尺寸、形状、位置等方面的数据。

这些数据需要按照一定的规范进行整理和记录，以便后续的分析和处理。

其次，我们需要对公差数据进行统计和分析。

统计分析能够帮助我们了解产品的制造过程中存在的问题，并找到解决问题的方法。

常用的统计分析方法包括均值、标准差、概率分布等。

通过对公差数据的统计分析，我们可以了解产品的尺寸偏差的分布情况，以及存在的异常情况。

此外，我们还需要进行公差数据的可视化处理。

可视化处理可以帮助我们更直观地了解公差数据的分布情况和变化趋势。

常用的可视化处理方法包括绘制直方图、散点图、箱线图等。

通过对公差数据的可视化处理，我们可以更加清楚地了解产品的尺寸偏差的分布情况，以及存在的异常情况。

最后，我们需要对公差数据进行合理的解释和应用。

在处理和分析公差数据的过程中，我们需要根据产品的设计要求和使用环境，对公差数据进行合理的解释。

通过合理解释公差数据，我们可以为产品的制造过程提供合理的指导和改进措施。

综上所述，公差数据处理与分析技巧对于确保产品质量和满足设计要求至关重要。

通过对公差数据的收集、整理、统计、分析和可视化处理，我们可以更好地了解产品的尺寸偏差情况，为产品的制造过程提供合理的指导和改进措施。

公差数据处理与分析技巧不仅可以提高产品的质量，还可以提高制造效率，降低成本，提升企业的竞争力。

统计公差分析方法概述公差分析方法是一种用于确定产品或系统中各种因素之间的相互关系和限制的工程方法。

它被广泛应用于各种制造和设计领域，包括机械、电子、航空航天、汽车等。

公差分析的目标是确保产品或系统在正常运行条件下能够满足设计要求。

本文将概述几种常见的公差分析方法。

一、基本术语和概念在介绍具体的公差分析方法之前，有必要先了解一些基本术语和概念。

1. 公差（Tolerance）：公差是指在设计和制造过程中所允许的误差或偏差范围。

公差可以是线性的，也可以是角度的。

2. 上限（Upper Limit）和下限（Lower Limit）：上限是指公差范围的最大值，下限是指公差范围的最小值。

3. 偏差（Deviation）：偏差是指产品或系统与其设计要求之间的差异。

4. 平均值（Mean）：平均值是指一系列测量值的算术平均数。

5. 标准偏差（Standard Deviation）：标准偏差是指一系列测量值与其平均值之间的平均差异。

6. Cp和Cpk指数：Cp指数是指一个过程的上下限规格范围与标准差之比。

Cpk指数是指一个过程的上限或下限与该过程能够达到的最大或最小值之间的差异与三倍的标准差之比。

二、公差分析方法1. 极差法（Range Method）极差法是一种简单直观的公差分析方法。

它通过测量一系列零件或产品的最大值和最小值来确定公差范围。

极差（Range）= 最大值 - 最小值优点：简单易懂，容易理解。

缺点：只考虑了最大值和最小值，没有考虑其他测量值的变化情况。

2. 平均偏差法（Average Deviation Method）平均偏差法是一种计算平均偏差和标准偏差的公差分析方法。

它可以提供关于产品或系统的整体偏差情况的信息。

平均偏差（Average Deviation）= 所有测量值的总和 / 测量值的个数标准偏差（Standard Deviation）= 各个偏差值与平均偏差之差的平方和的平均数的平方根优点：考虑了所有测量值的变化情况，能够提供更准确的分析结果。

在产品制造的过程中，工序是保证产品质量的最基本环节。

所谓工序能力是指处于稳定状态下的实际加工能力，工序能够稳定地生产出产品的能力，也就是说在操作者、机器设备、原材料、操作方法、测量方法和环境等标准条件下，工序呈稳定状态时所具有的加工精度。

工序能力分析是质量管理的一项重要的技术基础工作。

它有助于掌握各道工序的质量保证能力，为产品设计、工艺、工装设计、设备的维修、调整、更新、改造提供必要的资料和依据。

什么是CPK？CPK是Complex Process Capability index 的缩写，是现代企业用于表示制程能力的指标。

制程能力强才可能生产出质量、可靠性高的产品。

CPK的意义制程水平的量化反映;（用一个数值来表达制程的水平）制程力指数：是一种表示制程水平高低的方便方法，其实质作用是反映制程合格率的高低。

CPK等级评定及处理原则CPK计算公式Ca（Capability of Accuracy）:制程准确度；CP（Capability of Precision）:制程精密度；注意：计算CPK时，取样数据至少应有20组数据，方具有一定代表性。

统计公差分析方法概述；公差分析是克服误差传递干扰的一种合适方法，也是试验设计理论研究的有益扩充。

通俗地说，公差分析就是运用统计分析的方法，事先给众多输入X设置合理的公差（而不仅仅是目标值），以保证经过工艺流程之后，产生的输出Y对输入的变异不敏感，依然落在顾客要求或技术规范之内。

这个过程往往要求减小输入的公差，而减小输入的公差往往意味着产品加工成本的提高。

因此，公差分析还强调选择合适的输入变量，减小到合适的公差幅度，以确保工艺优化的成本最小化。

同时，一次成功的公差分析常常不是一蹴而就的，一般需要工艺工程师和统计工程师等多方协作、不断沟通反馈后才能完成。

一套完整的公差管理解决方案应体现全面质量管理的思想——全员参与和全过程管理，能够反映PDCA(Plan、Do、Check和Act)的方法——设计人员定义公差，工艺人员定义实现公差控制的方法(P);生产操作人员加工产品(D);检验人员对产品进行检验检测(C);设计人员和工艺人员要对实测数据进行判读，采取有效的改进措施(A)。

生产现场S H O P S O L U T I O N S金属加工汽车工艺与材料 A T&M2009年第7期50机械装配过程中，在保证各组成零件适当功能的前提下，各组成零件所定义的、允许的几何和位置上的误差称为公差。

公差的大小不仅关系到制造和装配过程，还极大影响着产品的质量、功能、生产效率以及制造成本。

公差信息是产品信息库中的重要内容，公差模型就是为表示公差信息而建立的数学及物理模型，它是进行公差分析的理论基础。

公差分析或称偏差分析，即通过已知零部件的尺寸分布和公差，考虑偏差的累积和传播，以计算装配体的尺寸分布和装配公差的过程。

公差分析的目的在于判断零部件的公差分布是否满足装配功能要求，进而评价整个装配的可行性。

早期公差分析方法面向的是一维尺寸公差的分析与计算。

Bjorke 则将公差分析拓展到三维空间。

Wang 、C h a s e 、P a b o n 、H o f f m a n 、Lee 、Turner 、Tsai 、Salomons 、Varghese 、Connor 等许多学者也分别提出了各自的理论和方法开展公差分析的研究。

此后，人工智能、专家系统、神经网络、稳健性理论等工具被引入公差分析领域当中，并分别构建了数学模型以解决公差分析问题。

1 公差模型公差模型可分为零件层面的公差信息模型和装配层面的公差拓扑关系模型。

Shan 提出了完整公差模型的建模准则，即兼容性和可计算性准则。

兼容性准则是指公差模型满足产品设计过程的要求，符合ISO 和ASME 标准，能够完整表述所有类型的公差。

可计算性准则是指公差模型可实现与CAD 系统集成、支持过/欠约束、可提取隐含尺寸信息、可识别公差类型，以检查公差分配方案的可行性等。

目前已经提出了很多公差模型表示法，但每一种模型都是基于一些假设，且只部分满足了公差模型的建模准则，至今尚未出现统一的、公认的公差模型。

以下将对几种典型的公差模型加以介绍和评价。

公差知识点总结公差的计算方法是先求出一组数据的平均数，然后将每个数据与平均数的差的绝对值求和，最后再除以数据的个数。

这样得到的就是这组数据的公差。

公差在实际应用中有着广泛的用途，特别是在质量管理、生产管理、金融和经济领域。

下面将从几个方面来介绍公差的知识点。

一、公差的计算方法1. 求平均数首先要求出一组数据的平均数，计算方法是将所有数据相加，然后除以数据的个数。

2. 求差的绝对值然后计算每个数据与平均数的差的绝对值。

3. 求和将每个数据与平均数的差的绝对值求和。

4. 求平均最后将上一步得到的和除以数据的个数，就得到了这组数据的公差。

二、公差的意义和作用1. 衡量数据分散程度公差可以帮助我们了解一组数据的分散程度，通过公差的大小，可以判断数据的离散程度和集中程度。

如果公差较大，说明数据的分散程度大，如果公差较小，说明数据的分散程度小。

2. 判断数据的质量在生产管理和质量管理中，公差可以帮助我们了解产品质量的一致性和稳定性。

公差越小，说明产品的质量越稳定，相反，公差越大，说明产品的质量波动越大。

3. 进行数据分析在统计学和经济学中，公差可以帮助我们进行数据分析，通过公差的计算可以判断数据的分布情况，从而更好地理解数据的特征和规律。

三、公差的影响因素1. 数据的大小数据的大小会直接影响公差的计算结果，数据越大，公差越大，反之亦然。

2. 数据的波动数据的波动程度也会影响公差的计算结果，数据波动越大，公差越大，反之亦然。

3. 数据的分布数据的分布情况也会影响公差的计算结果，如果数据分布比较均匀，公差可能会比较小，如果数据分布比较不均匀，公差可能会比较大。

四、公差的应用场景1. 质量和生产管理在生产和质量管理中，公差可以帮助我们了解产品质量的稳定性，通过公差的计算可以判断产品的质量是否符合要求。

2. 统计学分析在统计学中，公差可以帮助我们进行数据分析，通过公差的计算可以判断数据的分布情况，从而更好地理解数据的特征和规律。