当前位置：文档之家 › 第七章 二元离散选择模型

第七章 二元离散选择模型

  • 格式：ppt
  • 大小：1.17 MB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

离散选择模型ppt课件

离散选择模型ppt课件
2
因为通常情况下，我们考虑被解释变量为二元变
量的模型，这种模型也因此被称为二元选择模型或者离
散选择模型，如果为多元，则称之为多元选择模型。 离散选择模型起源于Fechner于1860年所进行的动
物条件二元反射研究，1962年Warner首次将这一方法
应用与经济研究领域。Mcfadden因为在离散选择模型
但问题是，当收入10万元，或者更少的情况下，平均拥有住房的
概率为负值，而当收入为20万元，或者更多的情况下，平均拥有 住房的概率大于1，因此，我们必须考虑相应的方法对这一问题 进行处理。
7
对同样的问题，我们采用如下的模型形式：
E (Yi / X i ) PYi 1 / X i
1
( 0 1 X i )
那么： 从而：
1 e Pi Li ln 1 P 0 1 X i ui i
1 ห้องสมุดไป่ตู้ Pi
1
0 1 X i
1 e e 0 1 X i 1 e 0 1 X i
参数的含义是什么？
这样的事件发生比Li，不仅对Xi是线性的，对参数也是线性的，而 且发生概率将永远落在0和1之间， Li就被称为logit，像*这样的模 型也就被称为logit模型。
Std. Err. .0041431 .0957771
[95% Conf. Interval] .069612 -1.879533 .0887202 -1.437808
e 1 e0.0792 1.082
这就意味着，当收入增加1万元时，根据该样本回归的结果认为， 拥有自有住房的发生比将增加8.2%
PYi 1 / X i
6

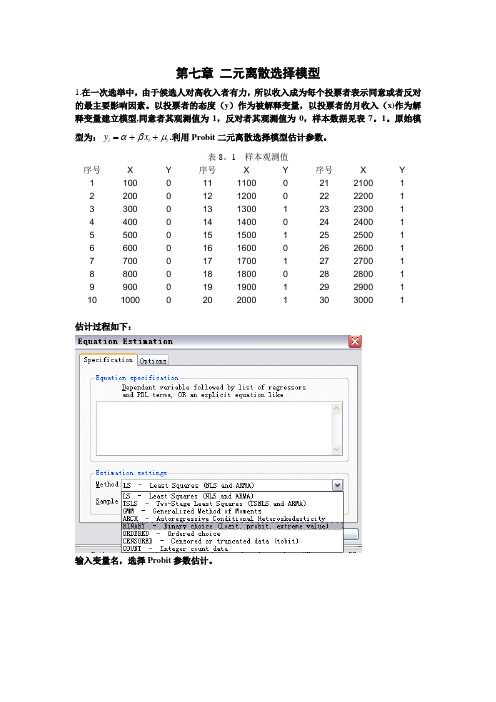
第七章二元离散选择模型

第七章二元离散选择模型

第七章 二元离散选择模型1.在一次选举中，由于候选人对高收入者有力，所以收入成为每个投票者表示同意或者反对的最主要影响因素。

以投票者的态度（y ）作为被解释变量，以投票者的月收入（x)作为解释变量建立模型,同意者其观测值为1，反对者其观测值为0，样本数据见表7。

1。

原始模型为：i i i y x αβμ=++.利用Probit 二元离散选择模型估计参数。

表8。

1 样本观测值 序号 X Y 序号 X Y 序号X Y 1 100 0 11 1100 0 21 2100 1 2 200 0 12 1200 0 22 2200 1 3 300 0 13 1300 1 23 2300 1 4 400 0 14 1400 0 24 2400 1 5 500 0 15 1500 1 25 2500 1 6 600 0 16 1600 0 26 2600 1 7 700 0 17 1700 1 27 2700 1 8 800 0 18 1800 0 28 2800 1 9 900 0 19 1900 1 29 2900 1 10100020 2000 13030001估计过程如下：输入变量名，选择Probit 参数估计。

得到如下输出结果：但是作为估计对象的不是原是模型，而是如下结果:YF CONRM X=---+1@[( 4.75390.003067*)]可以得到不通X值下的Y选择1的概率。

例如，当X=600时，查标准正态分布表，对应于2。

9137的累积正态分布为0。

9982；于是，Y的预测值YF=1—0.9982=0.0018,即对应于该个人,投赞成票的概率为0。

0018。

1.某商业银行从历史贷款客户中随机抽取78个样本，根据涉及的指标体系分别计算它们的“商业信用支持度”(XY ）和“市场竞争地位等级"（SC ），对它们贷款的结果(JG ）采用二元离散变量，1表示贷款成功，0表示贷款失败。

样本观测值见表8。

离散因变量和受限因变量模型

离散因变量和受限因变量模型

E ( yi ) P( yi 1) pi xi β
（7.1.3）
5
式(7.1.3)只有当xi 的取值在(0,1)之间时才成立，否则就会
产生矛盾，而在实际应用时很可能超出这个范围。因此，线性
概率模型常常写成下面的形式：
xi β, pi 1, 0,
0 xi β 1 xi β 1 xi β 0
* i * i
(7.1.9)
其中：F是ui*的分布函数，要求它是一个连续函数，并且是
单调递增的。因此，原始的回归模型可以看成如下的一个回
归模型：
yi 1 F xi β ui
即yi关于它的条件均值的一个回归。
(7.1.10)
8
分布函数的类型决定了二元选择模型的类型，根据分布函 数F的不同，二元选择模型可以有不同的类型，常用的二元选择 模型如表7.1所示： 表7.1 常用的二元选择模型
在离散选择模型中，最简单的情形是在两个可供选择的 方案中选择其一，此时被解释变量只取两个值，称为二元选 择模型（binary choice model）。在实际生活中，我们经常 遇到二元选择问题。例如，在买车与不买车的选择中，买车
记为1，不买记为0。是否买车与两类因素有关系：一类是车
本身所具有的属性，如价格、型号等；另一类是决策者所具 有的属性如收入水平、对车的偏好程度等。如果我们要研究 是否买车与收入之间的关系，即研究具有某一收入水平的个 体买车的可能性。因此，二元选择模型的目的是研究具有给
令pi = P ( yi =1) ，那么 1 - pi = P ( yi =0) ，于是
E ( yi ) 1 P( yi 1) 0 P( yi 0) pi
（7.1.2）

第七章 离散模型

第七章 离散模型

第七章 离散模型7.1 层次分析模型离散模型• 离散模型：差分方程（第7章）、整数规划（第4章）、图论、对策论、网络流、… … • 分析社会经济系统的有力工具• 只用到代数、集合及图论（少许）的知识● 背景1. 日常工作、生活中的决策问题2. 涉及经济、社会等方面的因素3. 作比较判断时人的主观选择起相当大的作用，各因素的重要性难以量化4. Saaty 于1970年代提出层次分析法 AHP (Analytic Hierarchy Process)5. AHP ——一种定性与定量相结合的、系统化、层次化的分析方法● 层次分析法的基本步骤例. 选择旅游地：如何在3个目的地中按照景色、费用、居住条件等因素选择.● “选择旅游地”思维过程的归纳1. 将决策问题分为3个层次：目标层O ，准则层C ，方案层P ；每层有若干元素， 各层元素间的关系用相连的直线表示。

2. 通过相互比较确定各准则对目标的权重，及各方案对每一准则的权重。

目标层准则层方案层3. 将上述两组权重进行综合，确定各方案对目标的权重。

层次分析法将定性分析与定量分析结合起来完成以上步骤，给出决策问题的定量结果。

● 层次分析法的基本步骤● 成对比较阵和权向量1. 元素之间两两对比，对比采用相对尺度；设要比较各准则C1,C2,… , Cn 对目标O的重要性。

ij j i a C C ⇒: ijji ij n n ij a a a a A 1,0,)(=>=⨯ 选择 A ~成对比较阵旅 A 是正互反阵 游地要由A 确定C1,… , Cn 对O 的权向量2. 成对比较的不一致情况不一致):(2/12112C C a = ):(43113C C a =允许不一致，但要确定不一致的允许范围3. 考察完全一致的情况⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1135/13/11125/13/13/12/117/14/1557123342/11A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=71242/11An w w w W ,,)1(21⇒=，j i ij w w a /=令，权向量~),,(21T n w w w w =，满足n k j i a a a ik jk ij ,,2,1,,, ==⋅的正互反阵A 称一致阵，如：● 一致阵性质1. A 的秩为1，A 的唯一非零特征根为n2. A 的任一列向量是对应于n 的特征向量3. A 的归一化特征向量可作为权向量对于不一致(但在允许范围内)的成对比较阵A ，建议用对应于最大特征根λ的特征向量作为权向量w ，即：w Aw λ=1. 比较尺度aijSaaty 等人提出1~9尺度——aij 取值1,2,… , 9及其互反数1,1/2, … , 1/9 便于定性到定量的转化：aij = 1,1/2, ,…1/9 j i C C :~的重要性与上面相反● 心理学家认为成对比较的因素不宜超过9个● 用1~3,1~5,…1~17,…,1p ~9p (p =2,3,4,5), d +0.1~d +0.9 (d =1,2,3,4)等27种比较尺度对若干实例构造成对比较阵，算出权向量，与实际对比发现， 1~9尺度较优。

离散选择模型

离散选择模型

Yi 0 1GPAi 2 INCOMEi ui
其中：
1 Yi 0
第i个学生拿到学士学位后三年内去读研 该生三年内未去读研
GPA=第i个学生本科平均成绩 INCOME=第i个学生家庭年收入（单位：千美元）
设回归结果如下（所有系数值均在10%水平统计上显著）：
ˆ Yi 0.7 0.4GPAi 0.002 INCOMEi
yi 0 yi 1
函数可以简化为：
L (1 F ( X ))1 yi F ( X ) yi
yi 1
对方程左右取对数我们便得到：
ln L [ yi ln F ( X ) (1 yi ) ln(1 F ( X ))]
i 1
n
似然函数为
fi ln L n yi fi [ (1 yi ) ]xi 0 Fi 1 Fi i 1
Pr ob(Y 1 X ) X F ( X ) f ( X ) X
因此我们在遇到二元响应模型时，估计出参数我们不能盲目的 将其解释为：解释变量变动一个单位，相对应的因变量变化参 数个单位。
为了解决偏效应的问题我们引入调整因子的概念。 在上式中的 f ( X ) 我们 便称为比例因子或调整因子，它与全部 的解释变量有关，为了方便起见，我们要找一个适用于模型所有 斜率的调整因子。有两种方法可以解决： （1）用解释变量的观测值计算偏效应的表达式，调整因子为：
四、二元选择模型的估计
1.除了LPM模型以外，二元选择模型的估计都是以极大似然法为基础 的 。由前面的讨论我们知道：
P(Y 1 X ) F ( X )
由此我们可以得到模型的似然函数为：
P(Y1 y1 ,Yn yn X ) (1 F ( X )) F ( X )

《离散选择模型》课件

《离散选择模型》课件

极大似然估计法
通过最大化似然函数，估计模型 的参数值。
差分法估计法
通过对变量的差分进行估计，减 少了共线性问题的影响。
一般化估计方程法
通过建立一般化估计方程，对参 数进行估计。
离散选择模型的应用
公共交通出行方式选择
分析人们在选择公共交通出行方式时的决策行为，为政府制定交通政策提供依据。
食品品牌选择
确定性
选择结果是确定的，参与者 不受随机因素的影响。
离散选择模型的数学模型
1Байду номын сангаас
多项式Logit模型
通过对选择概率进行建模，预测参与者选择各个选项的概率。
2
二项式Logit模型
基于二项分布，预测参与者是否选择某个选项。
3
线性概率模型
使用线性回归方法，预测选择某个选项的概率。
离散选择模型的参数估计方法
离散选择模型是一种描述人们在面临离散选择时决策行为的数学模型。
2 离散选择模型的应用领域
离散选择模型被广泛应用于诸多领域，如公共交通、市场营销和行为经济学等。
离散选择模型的基本假设
可比性
各个选择项之间可以进行比 较，存在客观标准用于决策。
独立性
参与者之间的选择行为是独 立的，不受其他参与者的影 响。
《离散选择模型》PPT课 件
离散选择模型是一种用于分析人们在面临离散选择时的决策行为的统计模型。 本课件将介绍离散选择模型的定义、基本假设、数学模型、参数估计方法、 应用、不足及未来发展方向。
什么是离散选择模型
离散选择模型是一种用于研究人们在面临可选项时所作出的离散决策行为的统计模型。
1 离散选择模型的定义
将离散选择模型与其他决策模 型进行结合，以提高模型的准 确性和解释能力。

离散选择模型ppt课件


PYi 1 / X i
6
例如，我们对一个是否拥有自有住房的案例进行回归，
结果如下： Yi 1.2009 0.1056X i (0.1483 ) (0.0087) R 0.8078
2
回归拟合的很好，经济学意义也非常明确，收入Xi每增加1单位 （1万元人民币），平均拥有住房的概率将增加10.56%：
11
2.解释变量同样为定性变量的情况
ቤተ መጻሕፍቲ ባይዱ
Pi Li ln 1 P 0 1 X i ui i P 1 ˆ Xi=1时： L1 ln 1 P 0 1 (1) 1 P0 ˆ Xi=0时： L0 ln 1 P 0 (2) 0 P 1 1 P 1 如果定义： OR P0 1 P 0 1 ˆ L ˆ 那么就有： lnOR L OR e 1 0 1
15
回归的结果如下：
. logit y x Iteration Iteration Iteration Iteration 0: 1: 2: 3: log log log log likelihood likelihood likelihood likelihood = = = = -253.69187 -242.36572 -242.32729 -242.32729 Number of obs LR chi2(1) Prob > chi2 Pseudo R2 Std. Err. .2910729 .1179409 z 4.50 -2.10 P>|z| 0.000 0.036 = = = = 366 22.73 0.0000 0.0448
这意味着在其他条件都相同的情况下，抽烟人士患食道癌的 可能性是不抽烟人士的3.7倍还要多。

第七章(下) 二元离散选择模型

基于上述LPM的缺点，在现实应用中，原始 模型一般不能作为实际研究二元选择问题的模型。
我们考虑对线性概率模型进行一些变换,来克服 这些缺点。
效用模型
用
U
1 i
表示第
i个个体选择1的效用，U
0 i
表示第
i个
个体选择0的效用。其效用均为随机变量，于是有
UUi0i1

X i X i
1 0
Yi* X i ui*
中，假定ui*的分布为极值分布，则该模型称为 Extreme模型。
第二节 二元离散选择模型最大似然估计
下面我们来构造二元离散选择模型的似然函数。这 是二元离散选择模型最关键的问题。
我们假设有以Y 轴为对称的概率密度函数f（.），则
P(Yi 1 ) P(Yi* 0 ) P( u*i X i ) 1 F ( X i ) F ( X i )
Yi f ( Xi ) F ( Xi )

X
i
(*)
于是我们选择F不同的形式得到不同的经验模型
ln L


N i 1

(1

Yi
)
1
f ( Xi ) F ( Xi )

Yi f ( Xi ) F ( Xi )

X
i
(*)
一、 Logit模型的最大似然估计
标Yi准* 正X态i分布ui*
x
F ( x)
Yi
10e(xYYxpii**()
0 x)0
1
e

z2 2
dz
2 则
逻辑分布
F(x)
Λ( x)
P(Yi 1) P(Yi* 标0准) 正态P概1(u率i* 分ex布p曲(X线xi) )logi1stic分F布(曲X线i )

离散选择模型举例-二元离散选择模型

一．二元离散选择模型1．二元响应模型(Binary response model)我们往往关心响应概率()()()()z G x x G x y x y k k =+++=E ==P βββ...1110，其中x 表示各种影响因素（各种解释变量，包括虚拟变量）。

根据不同的函数形式可以分为下面三类模型：线性概率模型（Linear probability model ，LPM ）、对数单位模型（logit ）、概率单位模型(probit)：三种模型估计的系数大约有以下的关系：L PM probit probit it ββββ5.2,6.1log ==2．偏效应（1）如果解释变量是一个连续型变量，那么他对p(x)=p(y=1|x)的偏效应可以通过求下面的偏导数得出来：()()()()dzz dG z g x g x x p j j =+=∂∂,0βββ，偏效应的符号和该解释变量对应的系数的符号一致；两个解释变量偏效应之比等于它们各自的估计系数之比。

（2）如果解释变量是一个离散性变量，则k x 从k c 变化到k c +1时对概率的影响大小为：()()()k k k k c x G c x G ββββββ+++-++++...1 (110110)上面的其他解释变量的取值往往取其平均值。

3．估计方法与约束检验极大似然估计；三种常见的大样本检验：拉格朗日乘数检验、wald 检验、似然比检验。

4．Stata 程序语法（以Probit 为例）probit depvar [indepvars] [weight] [if exp] [in range] [, level(#) nocoef noconstant robust cluster(varname) score(newvar) asis offset(varname) maximize_options ] predict [type] newvarname [if exp] [in range] [, statistic rules asif nooffset ] where statistic isp predicted probability of a positive outcome; the default xb linear predictionstdp standard error of the prediction二．具体的例子1．数据：美国1988年的CPS 数据2．模型：估计成为工会成员的可能性，模型形式如下：参加工会的概率=F(潜在经验potexp 、经验的平方项potexp2、受教育年限grade 、婚否married 、工会化程度high)；解释变量：Potexp=年龄-受教育年限-5；grade=完成的受教育年限；married ：1表示婚，0未婚；high ：1表示高度工会化的行业，否则为0。

第七章 二元离散选择模型和简单固定影响平行数据模型


(2)效用模型
U i1 X i 1 i1 U i0 X i 0 i0
第i个个体 选择1的效用 第i个个体 选择0的效用
U i1 U i0 X i (1 0 ) (i1 i0 )
yi* X i i*
作为研究对象的二元选择模型的基本形式：
• 对于
E ( yi ) P( yi 1) X i
问题在于：该式右端并没有处于[0，1]范围内 的限制，实际上很可能超出[0，1]的范围；而 该式左端，则要求处于[0，1]范围内。于是产 生了矛盾。
• 对于随机误差项 ，具有异方差性 。因为:
1 X i 当y i 1，其概率为X i i 当y i 0，其概率为1 X i X i
(3)最大似然估计
• 欲使得效用模型可以估计，就必须为随机误差 项选择一种特定的概率分布。
• 两种最常用的分布是标准正态分布和逻辑 （logistic）分布，于是形成了两种最常用的二 元选择模型—Probit模型和Logit模型。
• 最大似然函数及其估计过程如下：
构造（对数）似然函数：
P( yi 1) F (Xi )或者P( yi 0) 1 F (Xi )
(3)重复观测值可以得到情况下二元 logit离散选择模型的参数估计
• 对每个决策者有多个重复（例如10次左右）观 测值。 • 对第i个决策者重复观测ni次，选择yi=1的次数 比例为pi，那么可以将pi作为真实概率Pi的一个 估计量。
• 建立“对数成败比例模型” ，采用广义最小 二乘法估计 。 • 实际中并不常用。
伍得里奇 著，费建平、林相森
译，林少宫 校. 计量经
济学导论—现代观点. 中国人民大学出版社,2003 朱平芳 编著.现代计量经济学. 上海财经大学出版
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二元离散选择模型 Binary Discrete Choice Model
一、二元离散选择模型的经济背景
二、二元离散选择模型
三、二元Probit离散选择模型及其参数估计
四、二元Logit离散选择模型及其参数估计
五、一个实例
说明

在经典计量经济学模型中，被解释变量通常被假 定为连续变量。

离散被解释变量数据计量经济学模型（Models with Discrete Dependent Variables）和离散 选择模型(DCM, Discrete Choice Model)。
0.0 5 10 15 20 DF 25 30 35 40
2、重复观测值不可以得到情况下二元logit离散 选择模型的参数估计
ln L


n i 1
yi f i fi (1 y i ) X i Fi (1 Fi ) i 1
n i
(y
( X i )) X i 0
第i个个体 选择1的效用 第i个个体 选择0的效用
U i1 U i0 X i (1 0 ) (i1 i0 )
yi* X i i*
作为研究对象的二元选择模型
P( yi 1) P( yi* 0) P( i* X i )

注意，在模型中，效用是不可观测的，人们能够 得到的观测值仍然是选择结果，即1和0。
2
2)
2、重复观测值不可以得到情况下二元Probit离散
选择模型的参数估计
ln L


yi
fi Xi 1 Fi 0

yi
fi Xi F 1 i

i 1 n i 1
n
q i f ( q i X i ) Xi F ( q i X i )

对每个决策者有多个重复（例如10次左右） 观测值。 对第i个决策者重复观测ni次，选择yi=1的次 数比例为pi，那么可以将pi作为真实概率Pi的 一个估计量。


建立 “概率单位模型” ，采用广义 最小二乘法估计 。

实际中并不常用。
四、二元Logit离散选择模型及其参数 估计
1、逻辑分布的概率分布函数
n
• 在样本数据的支持下，如果知道概率分布函数 和概率密度函数，求解该方程组，可以得到模 型参数估计量。
三、二元Probit离散选择模型及其参数 估计
1、标准正态分布的概率分布函数
F (t )


t
( 2 )
12
exp( x 2 2) dx
f ( x ) (2 )
1
2
exp( x
1 pi P( y i 0)
于是 E ( y i ) 1 P( y i 1) 0 P( y i 0) p i 所以有
E(yi ) P(yi 1) Xi
• 对于
E ( yi ) P( yi 1) X i
问题在于：该式右端并没有处于[0，1]范围内 的限制，实际上很可能超出[0，1]的范围；而 该式左端，则要求处于[0，1]范围内。于是产 生了矛盾。

关于参数的非线性函数，不能直接求解，需采 用完全信息最大似然法中所采用的迭代方法。 应用计量经济学软件。

3、重复观测值可以得到情况下二元logit离 散选择模型的参数估计

对每个决策者有多个重复（例如10次左右）观 测值。 对第i个决策者重复观测ni次，选择yi=1的次数 比例为pi，那么可以将pi作为真实概率Pi的一个 估计量。
SC -2 -2 -2 -2 -2 -2 -2 -1 0 -2 -1 0 -2 0 -1 1 1 1 -1 -1 1 1 1 1 -1 0
JGF 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.9979 0.0000 0.0000 1.0000 0.0000 0.0000 0.0000 0.9998 0.9999 1.0000 0.4472 0.0000 0.0000 1.0000 1.0000 0.9999 0.0000 0.0000
例史贷款客户中随 机抽取78个样本，根据设计的指标体系分别计 算它们的“商业信用支持度”（XY）和“市场 竞争地位等级”（SC），对它们贷款的结果 （JG）采用二元离散变量，1表示贷款成功，0 表示贷款失败。目的是研究JG与XY、SC之间的 关系，并为正确贷款决策提供支持。
SC -2 0 0 -2 -1 2 -2 0 -2 -2 0 -1 2 -2 0 0 0 -1 -1 0 2 -2 -1 -2 0 -2
Probit 模型 Logit 模型 Extreme模型
(x )
e x (1 e x )
1 exp( e x )
五、例题
分析与建模： 在一次选举中，由于候选人对高收入者有 利，所以收入成为每个投票者表示同意或者 反对的最主要影响因素。以投票者的态度（y） 作为被解释变量，以投票者的月收入（x）作 为解释变量建立模型，同意者其观测值为1， 反对者其观测值为0。 原模型为：
F (t )
f (t )
.30 .25 .20
1 1 e
e (1 e
t
t t
F (t )
et
et 1 et
(t )
)
2
f (t )
1.0
(1 e )
t 2
(t )(1 (t ))
0.8
0.6 .15 0.4 .10 .05 .00 5 10 15 20 F 25 30 35 40 0.2
二元选择模型(Binary Choice Model)和多元选择 模型(Multiple Choice Model)。 本章只介绍二元选择模型。



离散选择模型起源于Fechner于1860年进行的动物 条件二元反射研究。 1962年，Warner首次将它应用于经济研究领域， 用以研究公共交通工具和私人交通工具的选择问 题。 70、80年代，离散选择模型被普遍应用于经济布 局、企业定点、交通问题、就业问题、购买决策 等经济决策领域的研究。 模型的估计方法主要发展于80年代初期。
二、二元离散选择模型
1、原始模型
Y X
y i X i i
其中Y为观测值为1和0的决策被解释变量，X 为解释变量，包括选择对象所具有的属性和选 择主体所具有的属性。
因为 E ( i ) 0 ，所以 E ( y i ) X i 。 令
pi P( y i 1)

模型估计结果
但是作为估计对象的不是原始模型，而是下 面这个模型。按照方程：
YF 1 @ CONRM [(4.7539 0.003067* X )]
可以得到不同X值下的Y选择1的概率。例如，当Ｘ ＝600时，查标准正态分布表，对应于2.0137的累 积正态分布为0.9982；于是，Ｙ的预测值 YF=1-0.9982=0.0018；即对应于该个人，投赞成 票 的概率为0.0018。
• 对于随机误差项 ，具有异方差性 。因为:
当yi 1，其概率为X i 1 Xi i 当yi 0，其概率为1 X i Xi
所以原始模型不能作为实际研究二元选择问题 的模型。
•
2、效用模型
U i1 X i 1 i1 U i0 X i 0 i0
yi xi i
样本观测值
xi
yi
xi
yi
xi
yi
100 200 300 400 500 600 700 800 900 1000
0 0 0 0 0 0 0 0 0 0
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000
0 0 1 0 1 0 1 0 1 1

欲使得效用模型可以估计，就必须为随机误差 项选择一种特定的概率分布。

两种最常用的分布是标准正态分布和逻辑 （logistic）分布，于是形成了两种最常用的二 元选择模型—Probit模型和Logit模型。
最大似然函数及其估计过程如下：

F (t ) 1 F (t )
标准正态分布或 逻辑分布的对称 性
很显然，如果不可观测的U1>U0，即对应于观测 值为1，因为该个体选择公共交通工具的效用大于 选择私人交通工具的效用，他当然要选择公共交 通工具； 相反，如果不可观测的U1≤U0，即对应于观测值 为0，因为该个体选择公共交通工具的效用小于选 择私人交通工具的效用，他当然要选择私人交通 工具。


3、最大似然估计
JG 0 0 0 0 0
XY 125.0 599.0 100.0 160.0 46.00 80.00 133.0 350.0 23.00 60.00 70.00 -8.000 400.0 72.00 120.0 40.00 35.00 26.00 15.00 69.00 107.0 29.00 2.000 37.00 53.00 194.0


建立“对数成败比例模型” ，采用广义最小 二乘法估计 。 实际中并不常用。

分布函数的类型决定了二元选择模型的类型，根据分布函 数F的不同，二元选择模型可以有不同的类型，常用的二元选择 模型如下表所示： 表 常用的二元选择模型
ui*对应的分布
标准正态分布 逻辑分布 极值分布
分布函数F
相应的二元选择模型
JG 0 0 1 0 0 1 0 1 0 0 1 0 1 0 1 1 1 0 0 0 1 0 0 0 1 0
XY 1500 96.00 -8.000 375.0 42.00 5.000 172.0 -8.000 89.00 128.0 6.000 150.0 54.00 28.00 25.00 23.00 14.00 49.00 14.00 61.00 40.00 30.00 112.0 78.00 0.000 131.0