最新全国卷3文科数学试题及参考答案
- 格式:doc
- 大小:1.18 MB
- 文档页数:17


绝密★启用前2020年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}1235711A =,,,,,,{}315|B x x =<<,则A ∩B 中元素的个数为 A .2 B .3 C .4 D .52.若)(1i 1i z +=-,则z = A .1–iB .1+iC .–iD .i3.设一组样本数据x 1,x 2,…,x n 的方差为0.01,则数据10x 1,10x 2,…,10x n 的方差为 A .0.01B .0.1C .1D .104.Logistic 模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位:天)的Logistic 模型:0.23(53)()=1e t I K t --+,其中K 为最大确诊病例数.当I (*t )=0.95K 时,标志着已初步遏制疫情,则*t 约为(ln19≈3)A .60B .63C .66D .695.已知πsin sin=3θθ++()1,则πsin =6θ+()A .12BC .23D6.在平面内,A ,B 是两个定点,C 是动点,若=1AC BC ⋅,则点C 的轨迹为 A .圆B .椭圆C .抛物线D .直线7.设O 为坐标原点,直线x =2与抛物线C :y 2=2px (p >0)交于D ,E 两点,若OD ⊥OE ,则C 的焦点坐标为 A .(14,0) B .(12,0) C .(1,0) D .(2,0)8.点(0,﹣1)到直线()1y k x =+距离的最大值为 A .1BCD .29.右图为某几何体的三视图,则该几何体的表面积是A .B .C .D .10.设a =log 32,b =log 53,c =23,则 A .a <c <bB .a <b <cC .b <c <aD .c <a <b11.在△ABC 中,cos C =23,AC =4,BC =3,则tan B = AB .C .D .12.已知函数f (x )=sin x +1sin x,则 A .f (x )的最小值为2B .f (x )的图像关于y 轴对称C .f (x )的图像关于直线x =π对称D .f (x )的图像关于直线2x π=对称 二、填空题:本题共4小题,每小题5分,共20分。



高考文科数学全国3卷附答案.._ - 绝密★启用前〔4〕某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。
图中 A 点表示十月的平均最高气温约为 0点_2021年普通高等学校招生全国统一考试15 C ,B _-_表示四月的平均最低气温约为_ -文科数学全国III卷5C 。
下面表达不正确的选项是__12页〕 A.各月的平均最低气温都在:-〔全卷共0 C 以上号- (适用地区:广西、云南、四川)学 - 本卷须知:B.七月的平均温差比一月的平均温差大__-1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两局部。
___-2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
C.三月和十一月的平均最高气温根本相同___ -3.答复选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
__D.平均气温高于的月份有5个_ 如需改动,用橡皮擦干净后,再选涂其它答案标号,答复非选择题时,将答案写在 20C_线__封答题卡上,写在本试卷上无效。
__ 密_ 4.考试结束后,将本试卷和答案卡一并交回。
__-_第I 卷 〔5〕小敏翻开计算机时,忘记了开机密码的前两位, 只记得第一位是 M,I,N 中的: -名 -一个字母,第二位是1,2,3,4,5 中的一个数字,那么小敏输入一次密码能够成功姓 一、选择题:此题共12小题,每题5分。
在每个小题给出的四个选项中,- 只有一项为哪一项符合题目要求的。
开机的概率是〔〕-〔1〕设集合A {0,2,4,6,8,10},B {4,8} ,那么C A B 〔 〕8111班 -A.B.C.D._15_15830_-__ A.{4,8} B.{0,2,6} C.{0,2,6,10} D.{0,2,4,6,8,10}1_-〔6〕假设tan_,那么cos2〔 〕年 -3__z__ 线〔2〕假设z4 3i ,那么 〔 〕高考文科数学全国3卷附答案__封z4114_A.B.C.D._ 密5555_ -__4 343 _-B .1D ._C.ii421_55 55_-〔7〕3 ,3,3 ,那么〔〕_a 2b 3c 25__ -___ -1 33 1_〔3〕向量 ,BC那么 ABC 〔〕A.bacB.a b cC.bcaD.cab_BA(,) ( ,),_ -2 22 2__-_:A.30B . 45C.60D.120a 4,b6,那么输出的n校-〔8〕执行右图的程序框图,如果输入的〔〕学-;...A.3 BC=8,AA 1=3,那么V 的最大值是B.4 A.4πB.9C.6πD. 32C.5 23D.6x 2 y 21(ab0)的左焦点,A ,B 分(12) O 为坐标原点,F 是椭圆C :22a b别为C 的左,右顶点.P 为C 上一点,且PF ⊥x 轴.过点A 的直线l 与线段PF交于点M ,与y 轴交于点E.假设直线BM 经过OE 的中点,那么C 的离心率为 A.1B.1C. 2D. 33 234第二卷边上的高等于1那么(9)在中,B= ,BC BC, sinA 〔〕ABC43A.3 B.10C. 5D.3101010510如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,那么该多面体的外表积为1836554185 90 81(11)在封闭的直三棱柱 ABC-A 1B 1C 1内有一个体积为 V 的球,假设AB BC ,AB=6,本卷包括必考题和选考题两局部。

2020年普通高等学校招生全国统一考试文科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}1,2,3,5,7,11A =,{}|315B x x =<<,则A B 中元素的个数为A. 2B. 3C. 4D. 52. 若(1)1z i i +=-,则z = A. 1i - B. 1i + C.i - D.i3.设一组样本数据12,,...,n x x x 的方差为0.01,则数据12n 10,10,...,10x x x 的方差为 A .0.01 B .0.1 C .1 D .104. Logistic 模型是常用数学模型之一,可应用于流行病学领域,有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数()t I (t 的单位:天)的Logistic 模型:()()0.23531t KI t e--=+,其中K 为最大确诊病例数.当()0.95I t K *=时,标志着已初步遏制疫情,则t *约为(In19≈3) A.60 B.63 C.66 D.695.已知sin sin()13πθθ++=,则sin()6πθ+= A.12C.23D.26.在平面内,,A B 是两个定点,C 是动点,若1AC BC ⋅=,则点C 的轨迹为 A. 圆 B. 椭圆 C. 抛物线 D. 直线7.设O 为坐标原点,直线2x =与抛物线2:2(0)C y px p =>交于,D E 两点,若OD OE ⊥,则C 的焦点坐标为A .1(,0)4B .1(,0)2C .(1,0)D .(2,0)8.点(0,1)-到直线(1)y k x =+距离的最大值为 A .1 B .2 C .3 D .29.右图为某几何体的三视图,则该几何体的表面积是A. 6+42B. 4+42C. 6+23D. 4+2310.设3log 2a =,5log 3b =,23c =,则 A .a c b << B.a b c << C. b c a << D. c a b <<11. 在ABC ∆中,2cos 3C =,4,3AC BC ==,则tan B =12. 已知函数1()sin sin f x x x=+,则 A. ()f x 的最小值为2B. ()f x 的图像关于y 轴对称C. ()f x 的图像关于直线x π=对称D. ()f x 的图像关于直线2x π=对称二、填空题:本题共4小题,每小题5分,共20分。

绝密★启用前2020年普通高等学校招生全国统一考试全国卷三文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}1235711,,,,,A =,{}315|B x x =<<,则A ∩B 中元素的个数为 A .2 B .3C .4D .5答案:B解析:由交集的定义可知A ∩B ={5711},,,故选B 2.若)(1i 1i z +=-,则z =A .1–iB .1+iC .–iD .i答案:C解析:因为)(1i 1i z +=-,所以21i (1i)2i i 1i (1i)(1i)2z ---====-++-,故选C 3.设一组样本数据x 1,x 2,…,x n 的方差为0.01,则数据10x 1,10x 2,…,10x n 的方差为A .0.01B .0.1C .1D .10答案:C解析:数据10x 1,10x 2,…,10x n 的方差等于数据x 1,x 2,…,x n 的方差210,即0.011001⨯=,故选C4.Logistic 模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数()I t (t 的单位:天)的Logistic 模型:0.23(53)()=1e t KI t --+,其中K 为最大确诊病例数.当*()0.95I t K =时,标志着已初步遏制疫情,则t *约为(ln193)≈A .60B .63C .66D .69答案:C解析:由0.23(53)()=1e t KI t --+可得ln 1()530.23K I t t ⎛⎫- ⎪⎝⎭=+-,所以若*()0.95I t K =时,*ln 1ln190.955353660.230.23K K t ⎛⎫- ⎪⎝⎭=+=+≈-,故选C. 5.已知πsin sin=3θθ++()1,则πsin =6θ+() A .12 BC .23 D答案:B解析:因为πsin sin =3θθ++()1,所以13sin sin sin 1226πθθθθθθ⎛⎫+=+=+= ⎪⎝⎭,所以πsin 6(+θ,故选B 6.在平面内,A ,B 是两个定点,C 是动点,若=1AC BC ⋅,则点C 的轨迹为A .圆B .椭圆C .抛物线D .直线答案:A解析:取线段AB 的中点O ,则AC OC OA =-,BC OC OB OC OA =-=+,因为=1AC BC ⋅,所以221OC OA -=,所以22||||1OC OA =+,即|||OC OA =C的轨迹为以线段AB 中点为A。

2024届高三一轮复习联考(三)全国卷文科数学试题注意事项:1.答卷前,考生务必将自己的姓名、考场号、座位号、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回,考试时间为120分钟,满分150分一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}212,1A xx B x x =<<=∣∣,则A B ⋃=()A.[)1,2-B.(),2∞-C.[)1,3- D.[]1,2-2.命题2:,220p x R x x ∀∈+-<的否定p ⌝为()A.2000,220x R x x ∃∈+->B.2,220x R x x ∀∈+-C.2,220x R x x ∀∈+->D.2000,220x R x x ∃∈+-3.3.已知复数2(1i)z =+(i 为虚数单位),则复数z 的虚部为()A.2B.2- C.2iD.2i-4.若函数()222,0,log ,0,x x x f x x x ⎧-=⎨>⎩则()2f f ⎡⎤-=⎣⎦()A.2- B.2 C.3- D.35.已知1sin 62πα⎛⎫-= ⎪⎝⎭,则2cos 23πα⎛⎫+= ⎪⎝⎭()A.14-B.14C.12-D.126.函数()21x xe ef x x --=+在[]3,3-上的大致图象为()A.B.C. D.7.函数2sin cos21y x x=-+的最小值是()A.3-B.1-C.32- D.12-8.已知数列{}n a的前n项和22nS n n m=-++,且对任意*1,0n nn N a a+∈-<,则实数m 的取值范为是()A.()2,∞-+ B.(),2∞--C.()2,∞+ D.(),2∞-9.已知等比数列()*a满足4221,m nq a a a≠=,(其中,*m n N∈),则91m n+的最小值为()A.6 B.16 C.32 D.210.已知函数()cos3f x xπ⎛⎫=+⎪⎝⎭,若()f x在[]0,a上的值域为11,2⎡⎤-⎢⎥⎣⎦,则实数a的取值范为()A.40,3π⎛⎤⎥⎝⎦B.24,33ππ⎡⎤⎢⎥⎣⎦C.2,3π∞⎡⎫+⎪⎢⎣⎭ D.25,33ππ⎡⎤⎢⎥⎣⎦11.设4sin1,3sin2,2sin3a b c===,则()A.a b c<< B.c b a<<C.c a b<< D.a c b<<12.已矨,,A B C均在球O的球面上运动,且满足3AOBπ∠=,若三棱锥O ABC-体积的最大值为6,则球O的体积为()A.12πB.48πC.D.二、填空题:本题共4小题,每小题5分,共20分.13.已知()(1,,a k b==,若a b⊥,则k=__________.14.已知{}n a是各项不全为零的等差数列,前n项和是n S,且2024S S=,若()2626nS S m=≠,则正整数m=__________.15.设,m n为不重合的直线,,,αβγ为不重合的平面,下列是αβ∥成立的充分条件的有()(只填序号).①,m a m β⊂∥②,,m n n m αβ⊂⊥⊥③,αγβγ⊥⊥④,m m αβ⊥⊥16.已知函数()14sin ,01,2,1,x x x f x x x π-<⎧=⎨+>⎩若关于x 的方程()()()2[]210f x m f x m --+-=恰有5个不同的实数解,则实数m 的取值集合为__________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分.17.(12分)已知数列{}n a 满足12122,log log 1n n a a a +==+,(1)求数列{}n a 的通项公式;(2)求(){}32nn a -的前n 项和nS.18.(12分)已知ABC 中,三个内角,,A B C 的对边分别为,,,,cos cos 2cos 4a b c C a A c C b B π=+=.(1)求tan A ;(2)若c =,求ABC 的面积.19.(12分)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,O 是BC 的中点,PB PC ==,22PD BC AB ===.(1)求证:平而PBC ⊥平面ABCD ;(2)求点A 到平面PCD 的距离.20.(12分)已知数列()n a 满足()21112122222326n n n n n a a a a n -+-++++=-⋅+ .(1)求{}n a 的通项公式;(2)若2n an n b a =+,求数列n b 的前n 项和T .21.(12分)已知函数()ln x af x ex x -=-+.(1)当1a =时,求曲线()f x 在点()()1,1f 处的切线方程,(2)当0a 时,证明,()2f x x >+.(二)选考题:共10分.请考生在第22,23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程](10分)在平面直角坐标系,xOy 中,直线l的参数方程为2,21,2x a y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为22413sin ρθ=+.(1)求直线l 和曲线C 的直角坐标方程;(2)若曲线C 经过伸缩变换,2,x x y y ⎧=⎪⎨⎪='⎩'得到曲线C ',若直线l 与曲线C '有公共点,试求a 的取值范围.23.[选修4-5:不等式选讲](10分)已知函数()22(0)f x x x t t =++->,若函数()f x 的最小值为5.(1)求t 的值;(2)若,,a b c 均为正实数,且2a b c t ++=,求1412a b c++的最小值.2024届高三一轮复习联考(三)全国卷文科数学参考答案及评分意见1.A【解析】由21x ,即()()110x x -+,解得11x -,所以{}11B xx =-∣,所以{12}A B xx ⋃=-<∣.故选A .2.D 【解析】2,220x x x ∀∈+-<R 的否定为:2000,220x x x ∃∈+-R ,故选D.3.A 【解析】2(1i)2i z =+=,即复数z 的虚部为2,故选A .4.D【解析】()()()222(2)228,8log 83f f -=--⨯-===,故选D.5.C 【解析】因为1sin 62πα⎛⎫-= ⎪⎝⎭,所以2211cos 2cos 2cos 22sin 11366622ππππααπαα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=--=--=-=- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦.故选C.6.A 【解析】()()2e e 1x xf x f x x ---==-+,所以函数()y f x =是奇函数,排除B 选项,又()22e e 215f --=>,排除C ,D 选项,故选A.7.D 【解析】由题意,函数22sin cos212sin 2sin y x x x x =-+=+,令[]sin 1,1t x =∈-,可得221122222y t t t ⎛⎫=+=+- ⎪⎝⎭,当12t =-,即1sin 2x =-时,函数取得最小值,最小值为12-.故选D.8.A【解析】因为10n n a a +-<,所以数列{}n a 为递减数列,当2n 时,()2212(1)2123n n n a S S n n m n n m n -⎡⎤=-=-++---+-+=-+⎣⎦,故可知当2n 时,{}n a 单调递减,故{}n a 为递减数列,只需满足21a a <,即112m m-+⇒-.故选A .9.D【解析】由等比数列的性质,可得()911911918,10102888m n m n m n m n m n n m ⎛⎛⎫⎛⎫+=+=++=+++= ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当6,2m n ==时,等号成立,因此,91m n +的最小值为2.故选D.10.B 【解析】()cos 3f x x π⎛⎫=+⎪⎝⎭,结合图象,()f x 的值域是11,,0,2333x a x a πππ⎡⎤-++⎢⎣⎦,于是533a πππ+,解得2433aππ,所以实数a 的取值范围为24,33ππ⎡⎤⎢⎥⎣⎦.故选B.11.B 【解析】设()()2sin cos sin ,x x x xf x f x x x -==',令()()cos sin ,sing x x x x g x x x =-'=-,当()0,x π∈时,()0g x '<,故()g x 在()0,π上递减,()()()00,0g x g f x <=∴<',故()sin xf x x=在()0,π上递减,023π<<< .()()sin3sin232,,2sin33sin232f f ∴<<<,故c b <,()()()sin 2012,sin1,sin22sin1,3sin232sin14sin12ππππππ-<<-<<<-<-<-,故b a <,故c b a <<,故选B.12.C 【解析】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时231133632212O ABC C AOB V V R R --==⨯⨯⨯==,故3R =O 的体积为343R V π==,故选C.13.3-【解析】0a b a b ⊥⇔⋅=,所以()(1,10,3k k ⋅=+==-.14.18【解析】设等差数列{}n a 的首项和公差分别为1,a d ,则2122n d d S n a n ⎛⎫=+- ⎪⎝⎭,所以n S 可看成关于n 的二次函数,由二次函数的对称性及202426,m S S S S ==,可得20242622m++=,解得18m =.15.④【解析】根据线面的位置关系易知,①②③中面α和面β可能相交也可能平行,④:若m α⊥且m β⊥,根据面面平行的判定可知垂直于同一直线的两平面互相平行,故④正确.16.()3,1--【解析】作出函数()f x 的大致图象,如图所示,令()t f x =,则()()()2[]210f x m f x m --+-=可化为()()()221110t m t m t m t --+-=-+-=,则11t =或21t m =-,则关于x 的方程()()()2[]210f x m f x m --+-=恰有5个不同的实数解等价于()t f x =的图象与直线12,t t t t ==的交点个数之和为5个,由图可得函数()t f x =的图象与直线1t t =的交点个数为2,所以()t f x =的图象与直线2t t =的交点个数为3个,即此时214m <-<,解得31m -<<-.17.【解析】(1)在数列{}n a 中,已知12122log log log 1n n n na a a a ++-==,所以12n na a +=,.即{}n a 是首项为12a =,公比为2的等比数列,所以()1*222n n n a n -=⨯=∈N .(2)由()()32322nn n a n -=-⨯,故()()231124272352322n n n S n n -=⨯+⨯+⨯++-⨯+-⨯ ,所以()()23412124272352322nn n S n n +=⨯+⨯+⨯++-⨯+-⨯ ,则()23123222322n n n S n +⎡⎤-=+⨯+++--⨯⎣⎦,()()()11212433221053212n n n n n ++-=-+⨯--⨯=-+-⋅-,故()110352n n S n +=+-⋅.18.【解析】(1)解法一:由题,cos cos 2cos a A c C b B +=,由正弦定理得,sin2sin cos sin cos B A A C C =+,.3,,sin2sin 2sin 2cos2422C A B C B A A A ππππ⎛⎫⎛⎫=++==-=-=- ⎪ ⎪⎝⎭⎝⎭,所以1cos2sin cos 2A A A -=+,221sin cos sin cos 2A A A A --=22tan 1tan 1tan 12A A A --=+,化简得2tan 2tan 30A A --=,解得tan 3A =或tan 1A =-(舍去).解法二:由题,cos cos 2cos a A c C b B +=,由正弦定理得,2sin2sin2sin2B A C =+,即()()()()2sin2sin sin B A C A C A C A C ⎡⎤⎡⎤=++-++--⎣⎦⎣⎦,即()()sin2sin cos B A C A C =+-,又A B C π++=,故()sin sin A C B +=,所以()2sin cos sin cos B B B A C =-,又0B π<<,故sin 0B ≠,所以()2cos cos B A C =-,又A B C π++=,故()cos cos B A C =-+,化简得sin sin 3cos cos A C A C =,因此tan tan 3A C =且tan 1C =,所以tan 3A =.(2)由(1)知tan 3A =,因此()tan tan tan tan 21tan tan A CB AC A C+=-+=-=-,.所以sin 10A =,sin 5B =2sin 2C =,因为,6sin sin a c a A C==,.所以1125sin 612225ABC S ac B ==⨯⨯= .19.【解析】(1)因为,PB PC O =是BC 的中点,所以PO BC ⊥,在直角POC 中,1PC OC ==,所以PO =,在矩形ABCD 中,1,2AB BC ==,所以DO =,又因为2PD =,所以在POD 中,222PD PO OD =+,即PO OD ⊥.而,,BC OD O BC OD ⋂=⊂平面ABCD ,所以PO ⊥平面ABCD ,而PO ⊂平面PBC ,所以平面PBC ⊥平面ABCD .'(2)由(1)平面PBC ⊥平面ABCD ,且DC BC ⊥,所以DC ⊥平面PBC ,所以DC PC ⊥,即PCD 是直角三角形,因为1PC CD ==,所以13122PDC S =⨯=,又知11212ACD S =⨯⨯= ,PO ⊥平面ABCD ,设点A 到平面PCD 的距离为d ,则A PCD P ACD V V --=,即1133PCD ACD S d S PO ⨯⨯=⨯⨯ ,即1311323d ⨯⨯=⨯⨯所以263d =,所以点A 到平面PCD 的距离为3..20.【解析】(1)由题当1n =时,()111223262a +=-⋅+=,即11a =.()21112122222326n n n n n a a a a n -+-++++=-⋅+ ①当2n 时,()211212222526n n n a a a n --+++=-⋅+ ②.①-②得()()()1223262526212nn n n n a n n n +=-⋅+--⋅-=-⋅,所以21n a n =-..(2)由(1)知,212221n an n n b a n -=+=+-,则()()()()3521212325221n n T n -=++++++++- ()()3521222213521n n -=+++++++++-⋅()()212214121232..1423nn n n n +⨯-+-+-=+=-21.【解析】(1)当1a =时,()()111e ln ,e 1x xf x x x f x x--=-+=-+',所以()()12,11f f '==,.则切线方程为()211y x -=⨯-,.即10x y -+=曲线()f x 在点()()1,1f 处的切线方程为10x y -+=.(2)证明:要证()2f x x >+,即证e ln 2x a x -->,设()eln ,0x aF x x x -=->,即证()2F x >,当0a 时,()()1e 1e ln ,ex a x ax ax F x x F x x x----=-=-='在()0,∞+上为增函数,且()e1x ah x x -=-中,()()0100e 110,1e 1e 10a a h h --=⨯-=-=-->.故()0F x '=在()0,∞+上有唯一实数根0x ,且()00,1x ∈..当()00,x x ∈时,()0F x '<,当()0,x x ∞∈+时,()0F x '>,从而当0x x =时,()F x 取得最小值.由()00F x '=,得001ex ax -=,故()()000001eln 2x aF x F x x x a a x -=-=+->.综上,当0a 时,()2F x >即()2f x x >+.22.【解析】(1)由题2,21,2x a t y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),消去参数t得直线:20l x a -=,.22413sin ρθ=+,即2224cos 4sin ρθθ=+,即曲线C 的直角坐标方程为2214x y +=.(2)由,2,x x y y ⎧=⎪⎨⎪='⎩'得2,,x x y y =⎧⎨=''⎩又2214x y +=,所以()()22214x y +'=',即'2'21x y +=,所以曲线C '的方程是221x y +=,.由1d =得11a -.所以a 的取值范围是[]1,1-.23.【解析】(1)()222f x x x t x x t x t =++-=++-+-,()2222y x x tx x t t t =++-+--=+=+,当2x t -时等号成立,.⋅又知当x t =时,x t -取得最小值,所以当x t =时,()f x 有最小值,此时()min ()25f x f t t ==+=,所以3t =..(2)由(1)知,23a b c ++=,()22141114111162(121)232333a b c a b c a b c ⎛⎫++=++++=++= ⎪⎝⎭,当且仅当333,,824a b c ===时取等号,所以1412a b c ++的最小值为163.。

绝密★启用前2021年普通高等学校招生全国统一考试文科数学本试卷共23题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
考前须知:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:此题共12小题,每题5分,共60分。
在每题给出的四个选项中,只有一项是符合题目要求的。
1.集合 A { 1,0,1,2},B {xx21},那么ABA. 1,0,1 B. 0,1 C. 1,1 D. 0,1,22.假设z(1 i) 2i,那么z=A.1 i B.1+i C.1 i D. 1+i3.两位男同学和两位女同学随机排成一列,那么两位女同学相邻的概率是1 1 1 1A. B. C.D.6 4 3 24.?西游记??三国演义??水浒传?和?红楼梦?是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过?西游记?或?红楼梦?的学生共有90位,阅读过?红楼梦?的学生共有80位,阅读过?西游记?且阅读过?红楼梦?的学生共有60位,那么该校阅读过?西游记?的学生人数与该校学生总数比值的估计值为A.0.5 B.0.6 C.0.7 D.0.85.函数 f(x) 2sinxsin2x 在[0,2π]的零点个数为A.2B.3C.4D.56.各项均为正数的等比数列{an}的前4项和为15,且a5=3a3+4a1,那么a3=A.16B.8C.4D.27x1aey=2x+b.曲线y ae xlnx在点〔,〕处的切线方程为,那么-1,b=1D.a=e-1,A.a=e,b=-1B.a=e,b=1C.a=e b1文科数学试题第1页〔共9页〕8.如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M 是线段ED的中点,那么A.BM=EN,且直线BM、EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM、EN是异面直线D.BM≠EN,且直线BM,EN是异面直线为,那么输出s的值等于9.执行下边的程序框图,如果输入的1A.2241B.2251C.2261D.22710.F是双曲线C:x2y21的一个焦点,点P在C上,O为坐标原点,假设OP=OF,45那么△OPF的面积为3579A.B.C.D .222211.记不等式组xy?6,表示的平面区域为D.命题p:(x,y)D,2xy?9;命题2x y0q:(x,y)D,2x y,12.下面给出了四个命题①pq②pq③pq④p q这四个命题中,所有真命题的编号是A.①③B.①②C.②③D.③④12.设fx是定义域为R的偶函数,且在0, 单调递减,那么132A.f〔log32〕>f〔23〕B.f〔log3〕>f〔2423〕>f〔23〕>f〔22〕3C.f〔22223〕>f〔23〕>f〔log31〕D.f〔23〕>f〔22〕>f〔log31〕44文科数学试题第2页〔共9页〕二、填空题:此题共4小题,每题5分,共20分。
绝密★启用前2021年普通高等学校招生全国统一考试〔新课标Ⅲ〕文科数学考前须知:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.答复选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答复非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每题5分,共60分。
在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
1.集合A={1,2,3,4},B={2,4,6,8},那么A⋂B中元素的个数为A.1 B.2 C.3 D.42.复平面内表示复数z=i(–2+i)的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.某城市为了解游客人数的变化规律,提高旅游效劳质量,收集并整理了2021年1月至2021年12月期间月接待游客量〔单位:万人〕的数据,绘制了下面的折线图.根据该折线图,以下结论错误的选项是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量顶峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比拟平稳4.4sin cos3αα-=,那么sin2α=A .79-B .29-C .29D .795.设x ,y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,那么z =x -y 的取值范围是 A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]6.函数f (x )=15sin(x +3π)+cos(x −6π)的最大值为A .65B .1C .35D .157.函数y =1+x +2sin xx的局部图像大致为A .B .C .D .8.执行下面的程序框图,为使输出S 的值小于91,那么输入的正整数N 的最小值为A .5B .4C .3D .29.圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,那么该圆柱的体积为 A .πB .3π4C .π2D .π410.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,那么A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.椭圆C :22221x y a b+=,〔a >b >0〕的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,那么C 的离心率为AB C D .1312.函数211()2()x x f x x x a ee --+=-++有唯一零点,那么a =A .12-B .13C .12D .1二、填空题:此题共4小题,每题5分,共20分。
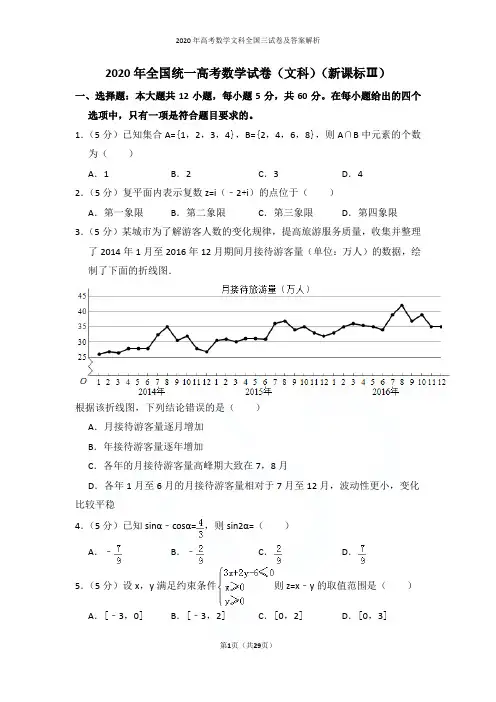
2020年全国统一高考数学试卷(文科)(新课标Ⅲ)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为()A.1B.2C.3D.42.(5分)复平面内表示复数z=i(﹣2+i)的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.(5分)已知sinα﹣cosα=,则sin2α=()A.﹣B.﹣C.D.5.(5分)设x,y满足约束条件则z=x﹣y的取值范围是()A.[﹣3,0]B.[﹣3,2]C.[0,2]D.[0,3]6.(5分)函数f(x)=sin(x+)+cos(x﹣)的最大值为()A.B.1C.D.7.(5分)函数y=1+x+的部分图象大致为()A.B.C.D.8.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N 的最小值为()A.5B.4C.3D.29.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB.C.D.10.(5分)在正方体ABCD﹣A1B1C1D1中,E为棱CD的中点,则()A.A1E⊥DC1B.A1E⊥BD C.A1E⊥BC1D.A1E⊥AC 11.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为()A.B.C.D.12.(5分)已知函数f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)有唯一零点,则a=()A.﹣B.C.D.1二、填空题13.(5分)已知向量=(﹣2,3),=(3,m),且,则m=.14.(5分)双曲线(a>0)的一条渐近线方程为y=x,则a=.15.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知C=60°,b=,c=3,则A=.16.(5分)设函数f(x)=,则满足f(x)+f(x﹣)>1的x的取值范围是.三、解答题17.(12分)设数列{a n}满足a1+3a2+…+(2n﹣1)a n=2n.(1)求{a n}的通项公式;(2)求数列{}的前n项和.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574以最高气温位于各区间的频率估计最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.19.(12分)如图四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.20.(12分)在直角坐标系xOy中,曲线y=x2+mx﹣2与x轴交于A、B两点,点C的坐标为(0,1),当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;(2)证明过A、B、C三点的圆在y轴上截得的弦长为定值.21.(12分)已知函数f(x)=lnx+ax2+(2a+1)x.(1)讨论f(x)的单调性;(2)当a<0时,证明f(x)≤﹣﹣2.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy中,直线l1的参数方程为,(t为参数),直线l2的参数方程为,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣=0,M为l3与C的交点,求M的极径.[选修4-5:不等式选讲]23.已知函数f(x)=|x+1|﹣|x﹣2|.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.2017年全国统一高考数学试卷(文科)(新课标Ⅲ)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分。
2020年普通高等学校招生全国统一考试(全国III 卷文科)数学试题注意事项:1.答题前,考生务必将自己的姓名、考生号、座位号填写在答题卡上。
本试卷满分150分。
2.作答时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合,,则A ∩B 中元素的个数为( ) A. 2 B. 3 C. 4 D. 52.若,则z =( )A. 1–iB. 1+iC. –iD. i3.设一组样本数据x 1,x 2,…,x n 的方差为0.01,则数据10x 1,10x 2,…,10x n 的方差为( )A. 0.01B. 0.1C. 1D. 104.Logistic 模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位:天)的Logistic 模型:,其中K 为最大确诊病例数.当I ()=0.95K 时,标志着已初步遏制疫情,则约为( )(ln19≈3)A. 60B. 63C. 66D. 695.已知,则( )A.C.D.6.在平面内,A,B 是两个定点,C 是动点,若,则点C 的轨迹为( )A. 圆B. 椭圆C. 抛物线D. 直线7.设O 为坐标原点,直线x =2与抛物线C :y 2=2px (p >0)交于D ,E 两点,若OD ⊥OE ,则C 的焦点坐标为( )A. (,0) B. (,0) C. (1,0) D. (2,0){}1235711A =,,,,,{}315|B x x =<<()11+=-z i i 0.23(53)()=1et I K t --+*t *t πsin sin =31θθ⎛⎫++ ⎪⎝⎭πsin =6θ⎛⎫+ ⎪⎝⎭12232=1AC BC ⋅14128.点(0,﹣1)到直线距离的最大值为( )A. 1B.C.D. 29.下图为某几何体的三视图,则该几何体的表面积是( )A. 6+4B. 4+4C. 6+2D. 4+210.设a =log 32,b =log 53,c =,则( ) A. a<c<b B. a<b<c C. b<c<a D. c<a<b 11.在△ABC 中,cos C =,AC =4,BC =3,则tan B =( ) A.B. 2C. 4D. 812.已知函数f (x )=sin x +,则( ) A. f(x)的最小值为2B. f(x)的图像关于y 轴对称C. f(x)的图像关于直线对称D. f(x)的图像关于直线对称二、填空题(本题共4小题,每小题5分,共20分.)13.若x ,y 满足约束条件 ,则z =3x +2y 的最大值为_________.14.设双曲线C : (a >0,b >0)的一条渐近线为y =x ,则C 的离心率为_________.15.设函数.若,则a =_________.16.已知圆锥底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________. 三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.) (一)必考题:共60分.17.设等比数列{a n }满足,. (1)求{a n }的通项公式;()1y k x =+232233232355551sin xx π=2x π=0,201,x y x y x +≥⎧⎪-≥⎨⎪≤⎩,22221x y a b -=2e ()xf x x a =+(1)4e f '=124a a +=318a a -=(2)记为数列{log 3a n }的前n 项和.若,求m .18.某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):(1(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?附:,n S 13m m m S S S +++=2()()()()()n ad bc K a b c d a c b d -=++++P (K 2≥k ) 0.050 0.010 0.001 k 3.8416.63510.82819.如图,在长方体中,点,分别在棱,上,且,.证明: (1)当时,; (2)点在平面内.20.已知函数. (1)讨论的单调性;(2)若有三个零点,求的取值范围.1111ABCD A B C D -E F 1DD 1BB 12DE ED =12BF FB =AB BC =EF AC ⊥1C AEF 32()f x x kx k =-+()f x ()f x k21.已知椭圆的离心率为,,分别为的左、右顶点.(1)求的方程;(2)若点在上,点在直线上,且,,求的面积.(二)选考题(共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.)[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,曲线C 的参数方程为(t 为参数且t ≠1),C 与坐标轴交于A ,B 两点. (1)求||:(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求直线AB 的极坐标方程.222:1(05)25x y C m m +=<<4A B C C P C Q 6x =||||BP BQ =BP BQ ⊥APQ 2222x t t y t t ⎧=--⎨=-+⎩,AB[选修4-5:不等式选讲]23.设a,b,c R,a+b+c=0,abc=1.(1)证明:ab+bc+ca<0;(2)用max{a,b,c}表示a,b,c中的最大值,证明:max{a,b,c2020年普通高等学校招生全国统一考试(全国III 卷文科)数学试题参考答案1-5.BDCCB 6-10ABBCA 11-12.CD 13.715.116.17.(1)设等比数列的公比为,根据题意,有,解得,所以;(2)令, 所以, 根据,可得, 整理得,因为,所以18.(1)由频数分布表可知,该市一天空气质量等级为的概率为,等级为的概率为,等级为的概率为,等级为的概率为; (2)由频数分布表可知,一天中到该公园锻炼的人次的平均数为(3)列联表如下:3{}n a q 1121148a a q a q a +=⎧⎨-=⎩113a q =⎧⎨=⎩13-=n n a 313log log 31n n n b a n -===-(01)(1)22n n n n n S +--==13m m m S S S +++=(1)(1)(2)(3)222m m m m m m -++++=2560m m --=0m >6m =的1216250.43100++=2510120.27100++=36780.21100++=47200.09100++=100203003550045350100⨯+⨯+⨯=22⨯空气质量好,因此,有的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关. 19.(1)因为长方体,所以平面, 因为长方体,所以四边形为正方形 因为平面,因此平面,因为平面,所以;(2)在上取点使得,连, 因为,所以所以四边形为平行四边形,因为所以四边形为平行四边形, 因此在平面内20. (1)由题,,当时,恒成立,所以在上单调递增; 当时,令,得,令,得, 令,得或,所以在上单调递减,在 ,上单调递增. (2)由(1)知,有三个零点,则,且228()21003383722 5.820 3.84155457030K ⨯⨯-⨯=≈>⨯⨯⨯95%1111ABCD A B C D -1BB ⊥ABCD ∴1AC BB ⊥1111,ABCD A B C D AB BC -=ABCD AC BD ∴⊥11,BB BD B BB BD =⊂、11BB D D AC ⊥11BB D D EF ⊂11BB D D AC EF ⊥1CC M 12CM MC =,DM MF 111112,//,=D E ED DD CC DD CC =11,//,ED MC ED MC =1DMC E 1//DM EC ∴//,=,MF DA MF DA MFAD 1//,//DM AF EC AF ∴∴1C AEF '2()3f x x k =-0k ≤'()0f x ≥()f x (,)-∞+∞0k >'()0f x =3k x =±'()0f x <33kkx -<<'()0f x >3kx <-3k x >()f x (,)33k k-(,)3k -∞-(,)3k+∞()f x 0k >()03()03kf kf ⎧->⎪⎪⎨⎪<⎪⎩即,解得, 当时,,且, 所以在上有唯一一个零点,同理,, 所以在上有唯一一个零点,又在上有唯一一个零点,所以有三个零点, 综上可知的取值范围为. 21.(1),,根据离心率, 解得或(舍), 的方程为:,即; (2)点在上,点在直线上,且,,过点作轴垂线,交点为,设与轴交点为根据题意画出图形,如图2220332033kk kk k k ⎧+>⎪⎪⎨⎪-<⎪⎩4027k <<4027k <<3kk >2()0f k k =>()f x (,)3kk 13kk --<-32(1)(1)0f k k k --=--+<()f x (1,)3kk ---()f x (,)33k k-()f x k 4(0,)27222:1(05)25x y C m m +=<<∴5a =b m =22154115c b m e a a ⎛⎫⎛⎫==-=-= ⎪ ⎪⎝⎭⎝⎭54m =54m =-∴C 22214255x y ⎛⎫ ⎪⎝⎭+=221612525x y +=P C Q 6x =||||BP BQ =BP BQ ⊥P x M 6x =x N,,,又,,,根据三角形全等条件“”, 可得:,, ,,设点为,可得点纵坐标为,将其代入,可得:,解得:或,点为或,①当点为时, 故,, ,可得:点为, 画出图象,如图,,可求得直线的直线方程为:, 根据点到直线距离公式可得到直线的距离为:, 根据两点间距离公式可得:,||||BP BQ =BP BQ ⊥90PMB QNB ∠=∠=︒90PBM QBN ∠+∠=︒90BQN QBN ∠+∠=︒∴PBM BQN ∠=∠AAS PMB BNQ ≅△△221612525x y +=∴(5,0)B ∴651PM BN ==-=P (,)P P x y P 1P y =221612525x y +=21612525P x +=3P x =3P x =-∴P (3,1)(3,1)-P (3,1)532MB =-=PMB BNQ ≅△△∴||||2MB NQ ==Q (6,2)(5,0)A -(6,2)Q AQ 211100x y -+=P AQ 22231111055125211d ⨯-⨯+===+()()22652055AQ =++-=面积为:;②当点为时,故,,,可得:点为,画出图象,如图,可求得直线的直线方程为:,根据点到直线距离公式可得到直线的距离为:,根据两点间距离公式可得:,面积为:,综上所述,面积为:.22.(1)令,则,解得或(舍),则,即. 令,则,解得或(舍),则,即.;(2)由(1)可知,则直线的方程为,即.由可得,直线的极坐标方程为.23.(1),.均不为,则,;(2)不妨设,∴APQ15555252⨯⨯=P(3,1)-5+38MB==PMB BNQ≅△△∴||||8MB NQ==Q(6,8)(5,0)A-,(6,8)Q AQ811400x y-+=P AQ()2283111405185185811d⨯--⨯+===+()()226580185AQ=++-=∴APQ1518522185⨯⨯=APQ520x=220t t+-=2t=-1t=26412y=++=(0,12)A 0y=2320t t-+=2t=1t=2244x=--=-(4,0)B-22(04)(120)410AB∴=++-=12030(4)ABk-==--AB3(4)y x=+3120x y-+=cos,sinx yρθρθ==AB3cos sin120ρθρθ-+=2222()2220a b c a b c ab ac bc++=+++++=()22212ab bc ca a b c∴++=-++,,a b c02220a b c++>()22212ab bc ca a b c∴++=-++<max{,,}a b c a=由可知,,,. 当且仅当时,取等号,,即.0,1a b c abc ++==0,0,0a b c ><<1,a b c a bc =--=()222322224b c b c bc bc bc a a a bc bc bc++++∴=⋅==≥=b c =a ∴≥3max{,,}4a b c。
绝密★启封并使用完毕前试题类型:新课标Ⅲ2017年普通高等学校招生全国统一考试文科数学本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共24题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑字迹的签字笔书写,字体工整,笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破,不准使用涂改液、修正液、刮纸刀。
第I 卷一、单选题 (本大题共12小题,每小题5分,共60分。
) 1. 已知集合{}{}1,2,3,4,2,4,6,8A B ==,则AB 中的元素的个数为( )A. 1B. 2C. 3D. 42. 复平面内表示复数()2z i i =-+的点位于( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A. 月接待游客量逐月增加B. 年接待游客量逐年增加C. 各年的月接待游客量高峰期大致在7,8月D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 4.已知4sin cos 3αα-=,则sin 2α=( ) A. 79-B. 29-C. 29D. 795. 设,x y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩则z x y =-的取值范围是( )A. []3,0-B. []3,2-C. []0,2D. []0,36. 函数()1sin cos 536f x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭的最大值为( )A.65 B. 1 C. 35 D. 157. 函数2sin 1xy x x =++的部分图像大致为( )8.执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A. 5B. 4C. 3D. 29. 已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A. πB.34π C.2π D. 4π 10. 在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则( )A.11A E DC ⊥B. 1A E BD ⊥C. 11A E BC ⊥D. 1A E AC ⊥11. 已知椭圆()2222:10x y C a b a b+=>>的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )A .63 B . 33 C . 23D . 1312. 已知函数()()2112x x f x x x a e e --+=-++有唯一零点,则a =( )A . 12-B . 13C . 12 D . 1 第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题、第(23)题为选考题,考生根据要求作答. 二、填空题 (本大题共4小题,每小题5分,共20分)13. 已知向量()2,3a =-,()3,b m =,且a b ⊥,则m =____。
14. 双曲线()222109x y a a -=>的一条渐近线方程为35y x =,则a =____。
15. ABC ∆内角,,A B C 的对边分别为,,a b c ,已知60,6,3C b c ===,则__.A = 16. 设函数()1,02,0x x x f x x +≤⎧=⎨>⎩则满足()112f x f x ⎛⎫+-> ⎪⎝⎭的x 的取值范围是_______。
三、简答题(本大题共6小题,共70分。
) 17. 设数列{}n a 满足()123...212n a a n a n +++-= (1)求数列{}n a 的通项公式;(2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和;18. 某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完。
根据往年销售经验,每天需求量与当天最高气温(单位:C )有关。
如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[)20,25,需求量为300瓶;如果最高气温低于20,需求量为200瓶。
为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频率分布表:以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y (单位:元)。
当六月份这种酸奶一天的进货量为450瓶时,写出Y 的所有可能值并估计Y 大于0的概率? 19. 如图,四面体ABCD 中,ABC ∆是正三角形,AD CD = (1)证明:AC BD ⊥(2)已知ACD ∆是直角三角形,AB BD=,若E 为棱BD 上与D 不重合的点,且AE EC ⊥,求四面体ABCE 与四面体ACDE 的体积比20. 在直角坐标系xOy 中,曲线22y x mx =+-与x 轴交于,A B 两点,点C 的坐标为(0,1)。
当m 变化时,解答下列问题: (1)能否出现AC BC ⊥的情况?说明理由;(2)证明过,,A B C 三点的圆在y 轴上截得的弦长为定值。
21. 设函数()()2ln 21f x x ax a x =+++.(1)讨论()f x 的单调性; (2)当0a <时,证明()324f x a<--. 22. 选考题:共10分。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
在直角坐标系xOy 中,直线1l 与参数方程为2,,x t y kt =+⎧⎨=⎩(t 为参数),直线2l 的参数方程为2x m m y k =-+⎧⎪⎨=⎪⎩(m 为参数),设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线C . (1) 写出C 的普通方程;(2) 以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设()3:cos sin 20l ρθθ+-=,M 为l 3与C 的交点,求M 的极径.23.选考题:共10分。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
已知函数f(x)=│x+1│–│x–2│.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2–x +m的解集非空,求m的取值范围.参考答案单选题1. B2. C3. A4. A5. B6. A7. D8. D9. B 10. C 11. A 12. C单选题 详解 1. 集合和集合有共同元素2,4,则所以元素个数为2.2. 化解得,所以复数位于第三象限。
3. 由折线图可知,每年月接待游客量从8月份后存在下降趋势,故选A .4.由题意易知,()216sin cos 9αα-=,1612sin cos 9αα∴-=,167sin 22sin cos 199ααα∴==-=-5.由题意,画出可行域,端点坐标 ,,.在端点处分别取的最小值与最大值.所以最大值为,最小值为.故选6.()111331sin cos sin cos cos sin 53652222f x x x x x x x ππ⎛⎫⎛⎫⎛⎫=++-=+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()3333sin 3cos sin 3cos 2sin 55553x x x x x π⎛⎫=+=+=⨯+ ⎪⎝⎭故最大值为657.注意到四个答案的差别,可以取一个较小的自变量值,比如0.01x =,则()()2sin 0.010.0110.01 1.0100.01f =++>>,故排除,A C 注意,B D 的差别,可取特别大的自变量,此时2sin xx 可忽略不计此时1y x ≈+,故排除B8. 当输入的正整数时,否,输出9.如图所示,易知11,2OA OB ==,32AB ∴=,233124S ππ⎛⎫∴=⨯= ⎪ ⎪⎝⎭,选B 10. 平面,又,平面,又平面.11. 易知圆心为原点,半径为a ,故圆心到直线20bx ay ab -+=的距离为半径即222aba a b=+ 2224b a b ∴=+ ()222233a b a c ∴==-2263cc e aa ∴===12. ()()()21111x x f x x a e e --+=--++令()()21g x x =-,则()g x 在(),1-∞上单调递减,在()1,+∞上单调递增;令()()11x x h x ee --+=+,则由均值不等式得,()h x 在(),1-∞上单调递减,在()1,+∞上单调递增;故当0a >时,()f x 在(),1-∞上单调递减,在()1,+∞上单调递增; ()1120f a ∴=-+=B OA102a ∴=>满足题意,结合选项知选C填空题 13. 2 14. 5 15. 75 16.填空题 详解 13. 因为得,。
14. 令双曲线右边的1为0,可得22209x y a -=,故双曲线的渐近线方程为3y x a=±5a ∴= 15. 有正弦定理知:sin sin B C b c=,3622sin 32B ⨯∴==,45B ∴=,故75A = 16.画出()f x 及12f x ⎛⎫- ⎪⎝⎭的图像知()f x 及12f x ⎛⎫- ⎪⎝⎭都是R 上的单调递增函数,故()12f x f x ⎛⎫+- ⎪⎝⎭也是R 上的单调递增函数,从图像上易判断()112f x f x ⎛⎫+-= ⎪⎝⎭的解在直线部分,故令1112x x +++=,解得14x =-,故()112f x f x ⎛⎫+-> ⎪⎝⎭的解集为1,4⎛⎫-+∞ ⎪⎝⎭简答题 17. (1)当时, (1分)当时,由① (2分)② (3分)① -②得(4分) 即x yf (x -12)-11f (x )验证符合上式 所以 (6分) (2) (8分)(12分) 18. 216363905P ++== (4分) 当温度大于等于时,需求量为,元 (6分) 当温度在时,需求量为, (8分)元 当温度低于时,需求量为,元 (10分) 当温度大于等于时,,3625744905P +++==。