七年级下册第一单元《平行线》探究题

浙教版七年级下册数学第一章平行线含答案一、单选题(共15题，共计45分)1、如图，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是（）。

A.同位角B.内错角C.对顶角D.同旁内角2、下列命题中，是假命题的是（）A.对顶角相等B.两点之间，线段最短C.互补的两个角不一定相等 D.同位角相等3、将一直角三角板与两边平行的硬纸条如图所示放置，下列结论：（1）∠1＝∠2；（2）∠3＝∠4；（3）∠2+∠4＝90°；（4）∠4+∠5＝180°. 其中正确的个数是( )A.1B.2C.3D.44、某同学在研究传统文化“抖空竹”时有一个发现：他把它抽象成数学问题，如图所示：已知，，，则的度数是（）A.38°B.44°C.46°D.56°5、如图，CD是△ABC的角平分线，DE∥BC．若∠A=60°，∠B=80°，则∠CDE 的度数是( )A.20°B.30°C.35°D.40°6、如图，两条直线a、b被第三条直线c所截，形成的同旁内角有（）A.2对B.4对C.6对D.8对7、如图，在条件：①∠5=∠6，②∠7=∠2，③∠3+∠8=180°，④∠3=∠2，⑤∠4+∠1=180°中，能判定a∥b的条件有（）A.4个B.3个C.2个D.1个8、下列抛物线平移后可得到抛物线y=-（x-2）2的是（）A.y=-x 2B.y=x 2-2C.y=（x-2）2+1D.y=（2-x）29、两条直线被第三条直线所截，就第三条直线上的两个交点而言形成了“三线八角”．为了便于记忆，同学们可仿照图用双手表示“三线八角”（两大拇指代表被截直线，食指代表截线）．下列三幅图依次表示（）A.同位角、同旁内角、内错角B.同位角、内错角、同旁内角C.同位角、对顶角、同旁内角D.同位角、内错角、对顶角10、如图，直线AB、CD被直线EF所截，AB∥CD，∠1=100°，则∠2等于（）A.70°B.80°C.90°D.100°11、如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）A.∠3=∠AB.∠1=∠2C.∠D=∠DCED.∠D+∠ACD=180°12、已知∠1与∠2是直线a与直线b被直线c所截得的内错角，且有∠1=50°，则∠2=（）A.130°B.50°C.80°D.无法确定13、小明将一直角三角板与两边平行的纸条如图放置．已知∠1=32°，则∠2的度数为( )A.32°B.48°C.58°D.68°14、如图，若∠1=∠2，DE∥BC，则下列结论：①FG∥DC；②∠AED=∠ACB；③CD平分∠ACB；④∠1+∠B=90°；⑤∠BFG=∠BDC。

浙教版七年级下册数学第一章平行线含答案一、单选题(共15题，共计45分)1、某同学在研究传统文化“抖空竹”时有一个发现：他把它抽象成数学问题，如图所示，已知，则的度数是（）A. B. C. D.2、如图．已知直线a，b被直线c所截，且a∥b，∠1＝48°，那么∠2的度数为（）A.42°B.48°C.52°D.132°3、如图所示，且，则的度数是（）A. B. C. D.4、在下面五幅图案中，(2)、(3)、(4)、(5)中哪一幅图案可以通过平移图案(1)得到A.(2)B.(3)C.(4)D.(5)5、观察下列个命题：其中真命题是（）.（ 1 ）直线、、，如果a⊥b、b⊥c ，那么a⊥c .（）三角形的三个内角中至少有两个锐角.（）平移变换中，各组对应点连成的两线段平行（或共线）且相等.（）三角形的外角和是.A.（）（）B.（）（）C.（）（）D.（）（）6、某城市几条道路的位置关系如图所示，已知AB∥CD，AE与AB的夹角为48°，若CF与EF的长度相等，则∠C的度数为（）A.48°B.40°C.30°D.24°7、▱ABCD中，AD＝8，∠BAD的平分线交BC于E，∠ADC的平分线交BC于F，且EF＝2，则AB的长是（）A.5B.3C.3或5D.2或38、如图，将一副三角板如此摆放，使得BO和CD平行，则∠AOD的度数为（）A.10°B.15°C.20°D.25°9、下列说法中正确的是（）A.过一点有且只有一条直线平行于已知直线B.从直线外一点到这条直线的垂线段，叫做点到这条直线的距离C.平移不改变图形的大小和形状 D.不相交的两条直线叫做平行线10、如图，已知AB∥CD，直线EF分别交AB，CD于点E，F，EG平分∠BEF，若∠1=48°，则∠2的度数是( )A.64°B.65°C.66°D.67°11、如图，下列四个角中，与∠1构成一对同位角的是（）A.∠2B.∠3C.∠4D.∠512、下列说法正确的是（）A.相等的角是对顶角B.同旁内角相等，两直线平行C.直线外一点到这条直线的垂线段，叫做点到直线的距D.经过直线外一点，有且只有一条直线与这条直线平行13、将一副三角尺按如图的方式摆放，其中l1∥l2，则∠α的度数是( )A.30°B.45°C.60°D.70°14、在平移过程中，对应线段（）A.互相平行且相等B.互相垂直且相等C.在一条直线上D.互相平行（或在同一条直线上）且相等15、过一点画已知直线的平行线（）A.有且只有一条B.不存在C.有两条D.不存在或有且只有一条二、填空题(共10题，共计30分)16、如图，将一副三角板和一张对边平行的纸条按如图方式摆放，则∠α的度数是________.17、完成下面推理过程：如图，已知DE∥BC，DF、BE分别平分∠ADE、∠ABC，可推得∠FDE=∠DEB的理由：∵DE∥BC（已知）∴∠ADE=________．（________ ）∵DF、BE分别平分∠ADE、∠ABC，∴∠ADF=________∠ABE=________ ．（________ ）∴∠ADF=∠ABE∴DF∥________．（________）∴∠FDE=∠DEB．（________ ）18、如图，直线a∥b，直线c与直线a、b分别相交于A、B两点，若∠1=60°，则∠2=________．19、如图，已知AB∥CD，∠A=60°，∠C =25°，则∠E=________度．20、如图，AB∥CD，AD、BC相交于O，且AO=5，BO=4，CO=16，那么DO=________；21、如图，一把直尺沿直线断开并错位，点E、D、B、F在同一直线上，若∠ADE=145°，则∠DBC的度数为________．22、把下面的说理过程补充完整：已知：如图，，，．线段AB和线段DE平行吗？请说明理由．解：理由：(已知)．(________)即又(________)(________)(________)．(________)．23、如图，已知∠MON＝30°，点A1，A2，A3，…在射线ON上，点B1，B，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边2三角形，若OA1＝1，则△A8B8A9的边长________。

苏科版七年级数学下册直线平行的条件和探索【直线平行的条件和性质】【学习目标】1.同位角、内错角、同旁内角的识别；2.会判定两条直线平行；3.平行线的性质.【基础知识梳理】1．如图，同位角的是；内错角的是；同旁内角的是．2．直线平行的条件：（1）基本事实：，两直线平行；（2）定理：，两直线平行；（3）定理：，两直线平行．3．平行线的性质：（1）基本事实：两直线平行，；（2）定理：两直线平行，；（3）定理：两直线平行，．【典型例题】一、三线八角模型例1：如图所示，同位角一共有对，分别是；内错角一共有对，分别是；同旁内角一共有对，分别是．【变式】已知：如图是一个跳棋棋盘，其游戏规则是：一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角．跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上.例如：从起始位置∠1跳到终点位置∠3写出其中两种不同路径，路径1：∠1一同旁内角→∠9一内错角→∠3．路径2：∠1一内错角→∠12一内错角→∠6一同位角→∠10一同旁内角→∠3．试一试：（1）从起始∠1跳到终点角∠8；（2）从起始角∠1依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点∠8？二、平行线的判定例2：如图，点E在AC的延长线上，给出四个条件：①∠1＝∠2；②∠3＝∠4：③∠A＝∠DCE；④∠D+∠ABD＝180°．其中能判断AB∥CD的有．（填写所有满足条件的序号）三、平行线的性质例3：如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE＝18°，求图2中∠AEF的度数.【变式】如图，AB⊥BC，DC⊥BC，E是BC上一点，EM⊥EN，∠EMA和∠END的平分线交于点F，求∠F的度数.四、综合运用例4：填空并完成以下证明：已知，如图，∠1＝∠ACB，∠2＝∠3，FH⊥AB于H，求证：CD⊥AB．证明：FH⊥AB（已知）∴∠BHF＝．∵∠1＝∠ACB（已知）∴DE∥BC（）∴∠2＝．（）∵∠2＝∠3（已知）∴∠3＝．（）∴CD∥FH（）∴∠BDC＝∠BHF＝．°（）∴CD⊥AB．例5：（1）如图(1)，若∠B+∠D＝∠BED，试猜想AB与CD的位置关系，并说明理由；（2）如图(2)，要想得到AB∥CD，则∠1、∠2、∠3之间应满足怎样的数量关系，试说明理由．【变式】问题情境：如图1，AB∥CD，∠P AB＝130°，∠PCD＝120°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC＝50°+60°＝110°．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．【拓展应用】例6：如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．（1）试判断直线AB与直线CD的位置关系，并说明理由；（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK＝∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．【能力提升】1．如图所示，下列结论中不正确的是（）A．∠1和∠2是同位角B．∠2和∠3是同旁内角C．∠1和∠4是同位角D．∠2和∠4是内错角2．在同一个平面内，不相邻的两个直角，如果它们有一条边共线，那么另一边互相（）A．平行B．垂直C．共线D．平行或共线3．如图，F A⊥MN于A，HC⊥MN于C，指出下列各判断中，错误的是（）A．由∠CAB＝∠NCD，得AB∥CD B．由∠DCG＝∠BAC，得AB∥CDC．由∠MAE＝∠ACG，∠DCG＝∠BAE，得AB∥CD D．由∠MAB＝∠ACD，得AB∥CD4．如图，在△ABC中，以点C为顶点，在△ABC外画∠ACD＝∠A，且点A与D在直线BC的同一侧，再延长BC至点E，在所作的图形中，∠A与是内错角；∠B与是同位角；∠ACB与是同旁内角．5．如图，已知∠1＝（3x +24）°，∠2＝（5x +20）°，要使m ∥n ，那么∠1＝ （度）．6．如图，BE ∥CF ，则∠A +∠B +∠C +∠D ＝ 度．7.如图，直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交，若∠1＝30°，求∠2的度数.8.（1）如图①，若∠B +∠D ＝∠BED ，试猜想AB 与CD 的位置关系，并说明理由；（2）如图②，要想得到AB ∥CD ，则∠1、∠2、∠3之间应满足怎样的数量关系，试说明理由．9.如图，AD ∥BC ，∠DAC ＝120°，∠ACF ＝20°，∠EFC ＝140°．求证：EF ∥AD ．10.【探究】如图①，∠AFH 和∠CHF 的平分线交于点O ，EG 经过点O 且平行于FH ，分别与AB 、CD 交于点E 、C ．（1）若∠AFH ＝60°，∠CHF ＝50°，则∠EOF ＝ 度，∠FOH ＝ 度．（2）若∠AFH +∠CHF ＝100°，求∠FOH 的度数．【拓展】如图②，∠AFH 和∠CHI 的平分线交于点O ，EG 经过点O 且平行于FH ，分别与AB 、CD 交于点E 、G ．若∠AFH +∠CHF ＝α，直接写出∠FOH 的度数．（用含α的代数式表示）【能力提升】答案第1题 第3题 第4题 第5题 第6题1．如图所示，下列结论中不正确的是（）A．∠1和∠2是同位角B．∠2和∠3是同旁内角C．∠1和∠4是同位角D．∠2和∠4是内错角解：A、∠1和∠2是同旁内角，故本选项错误，符合题意；B、∠2和∠3是同旁内角，故本选项正确，不符合题意；C、∠1和∠4是同位角，故本选项正确，不符合题意；D、∠3和∠4是内错角，故本选项正确，不符合题意；故选：A．2．在同一个平面内，不相邻的两个直角，如果它们有一条边共线，那么另一边互相（）A．平行B．垂直C．共线D．平行或共线解：如图所示：不相邻的两个直角，如果它们有一条边共线，内错角相等，或同旁内角互补，那么另一边互相平行或共线．故选：D．3．如图，F A⊥MN于A，HC⊥MN于C，指出下列各判断中，错误的是（）A．由∠CAB＝∠NCD，得AB∥CDB．由∠DCG＝∠BAC，得AB∥CDC．由∠MAE＝∠ACG，∠DCG＝∠BAE，得AB∥CDD．由∠MAB＝∠ACD，得AB∥CD解：A、正确，同位角∠CAB＝∠NCD，故AB∥CD；B、错误，∠DCN＝∠BAC不是同位角，所以B不对；C、正确，∠MAE＝∠ACG，∠DCG＝∠BAE，可得同位角∠BAN＝∠DCN，故AB∥CD；D、正确，同位角∠MAB＝∠ACD，故AB∥CD．故选：B．4．如图，在△ABC中，以点C为顶点，在△ABC外画∠ACD＝∠A，且点A与D在直线BC的同一侧，再延长BC至点E，在作的图形中，∠A与是内错角；∠B与是同位角；∠ACB与是同旁内角．解：如图所示，∠A与∠ACD、∠ACE是内错角；∠B与∠DCE、∠ACE是同位角；∠ACB与∠A、∠B是同旁内角．5．如图，已知∠1＝（3x+24）°，∠2＝（5x+20）°，要使m∥n，那么∠1＝75（度）．解：如图所示：∠1+∠3＝180°，∵m∥n，∴∠2＝∠3，∴∠1+∠2＝180°，∴3x+24+5x+20＝180°，解得：x＝17，则∠1＝（3x+24）°＝75°．6．如图，BE∥CF，则∠A+∠B+∠C+∠D＝180度．解：如图所示，由图知∠A+∠B＝∠BPD，∵BE∥CF，∴∠CQD＝∠BPD＝∠A+∠B，又∵∠CQD+∠C+∠D＝180°，∴∠A+∠B+∠C+∠D＝180°.7.如图，直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交，若∠1＝30°，求∠2的度数.解：如图，∵∠ACB＝90°∴∠1+∠3＝90°，∵∠1＝30°，∴∠3＝60°，∵a∥b，∴∠2＝∠3＝60°.8.（1）如图①，若∠B+∠D＝∠BED，试猜想AB与CD的位置关系，并说明理由；（2）如图②，要想得到AB∥CD，则∠1、∠2、∠3之间应满足怎样的数量关系，试说明理由．解：（1）AB∥CD，理由：如图（1），延长BE交CD于F．∵∠BED＝∠B+∠D，∠BED＝∠EFD+∠D，∴∠B＝∠EFD，∴AB∥CD；（2）∠1＝∠2+∠3．理由如下：如图（2），延长BA交CE于F，∵AB∥CD（已知），∴∠3＝∠EF A（两直线平行，同位角相等），∵∠1＝∠2+∠EF A，∴∠1＝∠2+∠3．9.如图，AD∥BC，∠DAC＝120°，∠ACF＝20°，∠EFC＝140°．求证：EF∥AD．证明：∵AD∥BC，∴∠DAC+∠ACB＝180°，∵∠DAC＝120°，∴∠ACB＝60°，又∵∠ACF＝20°，∴∠BCF＝∠ACB－∠ACF＝40°，又∵∠EFC＝140°，∴∠BCF+∠EFC＝180°，∴EF∥BC，∵AD∥BC，∴EF∥AD．10. 【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．（1）若∠AFH＝60°，∠CHF＝50°，则∠EOF＝度，∠FOH＝度．（2）若∠AFH+∠CHF＝100°，求∠FOH的度数．【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF ＝α，直接写出∠FOH的度数．（用含α的代数式表示）解：【探究】（1）∵∠AFH＝60°，OF平分∠AFH，∴∠OFH＝30°，又∵EG∥FH，∴∠EOF＝∠OFH＝30°；∵∠CHF＝50°，OH平分∠CHF，∴∠FHO＝25°，∴△FOH中，∠FOH＝180°－∠OFH－∠OHF＝125°；故答案为：30，125；（2）∵FO 平分∠AFH ，HO 平分∠CHF ，∴∠OFH ＝12 ∠AFH ，∠OHF ＝12∠CHF ． ∵∠AFH +∠CHF ＝100°，∴∠OFH +∠OHF ＝12 （∠AFH +∠CHF ）＝12×100°＝50°． ∵EG ∥FH ，∴∠EOF ＝∠OFH ，∠GOH ＝∠OHF ．∴∠EOF +∠GOH ＝∠OFH +∠OHF ＝50°．∵∠EOF +∠GOH +∠FOH ＝180°，∴∠FOH ＝180°－（∠EOF +∠GOH ）＝180°－50°＝130°．【拓展】∵∠AFH 和∠CHI 的平分线交于点O ，∴∠OFH ＝12 ∠AFH ，∠OHI ＝12∠CHI ， ∴∠FOH ＝∠OHI －∠OFH＝12（∠CHI －∠AFH ） ＝12（180°－∠CHF －∠AFH ） ＝12（180°－α） ＝90°－12α．。

初一数学《相交线与平行线》及探究题、答案解析知识要点：1. 两条直线的位置关系（1）在同一平面内，两条直线的位置关系有两种：相交与平行． （2）平行线：在同一平面内，不相交的两条直线叫平行线． 2. 几种特殊关系的角（1）余角和补角：如果两个角的和是直角，称这两个角互为余角．如果两个角的和是平角，称这两个角互为补角．（2）对顶角：①定义：一个角的两边分别是另一个角两边的反向延长线，这两个角叫对顶角． ②性质：对顶角相等．（3）同位角、内错角、同旁内角两条直线分别与第三条直线相交，构成八个角．①在两条直线之间并且在第三条直线的两旁的两个角叫做内错角． ②在两条直线的同一侧并且在第三条直线同旁的两个角叫做同位角． ③在两条直线之间并且在第三条直线同旁的两个角叫做同旁内角． 3. 主要的结论 （1）垂线①过一点有且只有一条直线与已知直线垂直．②直线外一点与直线上各点连结的所有线段中，垂线段最短．简称：垂线段最短． （24. 几个概念（1）垂线段：过直线外一点，作已知直线的垂线，这点和垂足之间的线段． （2）点到直线的距离：从直线外一点到这条直线的垂线段的长度． 5. 几个基本图形（1）相交线型．①一般型（如图①）；②特殊型（垂直，如图②）．（2）三线八角．①一般型（如图①）；②特殊型（平行，如图②）．ABC DOABCDO ①②重点难点：重点有两个：一方面要掌握关于相交线和平行线的一些基本事实，另一方面学会借助三角尺上的直角或量角器画已知直线的垂线，用移动三角尺的方法画平行线．难点是是利用对顶角的性质、平行线的特征、两直线平行的条件等进行推理和计算．考点分析：考查（1）对顶角的性质；（2）平行线的识别方法；（3）平行线的特征，其中依据平行线的识别与特征解决一类与平行线有关的几何问题是历届中考命题的重要考点．常见题型有填空题、选择题和解答题，单纯考查一个知识点的题目并不难，属于中低档题，将平行线的特征与其他知识综合起来考查的题目难度较大，属高档题．【典型例题】1. 如图所示，已知FC ∥AB ∥DE ，∠α∶∠D ∶∠B ＝2∶3∶4，求∠α、∠D 、∠B 的度数．2. 如图所示，直线a ∥b ，则∠A ＝__________．3．如图1，直线MN 与直线AB 、CD 分别交于点E 、F ，∠1与∠2互补． （1）试判断直线AB 与直线CD 的位置关系，并说明理由；A BCDEFAB CDEF①②ABC DEF12αABCEa b28°50°（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．4．已知，BC∥OA，∠B=∠A=100°，试回答下列问题：（1）如图①，求证：OB∥AC．（2）如图②，若点E、F在线段BC上，且满足∠FOC=∠AOC，并且OE平分∠BOF．则∠EOC的度数等于；（在横线上填上答案即可）．（3）在（2）的条件下，若平行移动AC，如图③，那么∠OCB：∠OFB的值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值．（4）在（3）的条件下，如果平行移动AC的过程中，若使∠OEB=∠OCA，此时∠OCA度数等于．（在横线上填上答案即可）．5．如图，已知两条射线OM∥CN，动线段AB的两个端点A、B分别在射线OM、CN上，且∠C=∠OAB=108°，F在线段CB上，OB平分∠AOF，OE平分∠COF．（1）请在图中找出与∠AOC相等的角，并说明理由；（2）若平行移动AB，那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值；（3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=2∠OBA？若存在，请求出∠OBA度数；若不存在，说明理由．6．已知E，F分别是AB、CD上的动点，P也为一动点．（1）如图1，若AB∥CD，求证：∠P=∠BEP+∠PFD；（2）如图2，若∠P=∠PFD﹣∠BEP，求证：AB∥CD；（3）如图3，AB∥CD，移动E，F使得∠EPF=90°，作∠PEG=∠BEP，求的值．7．已知：∠A=（90+x）°，∠B=（90﹣x）°，∠CED=90°，射线EF∥AC，2∠C﹣∠D=m．（1）判断AC与BD的位置关系，并说明理由．（2）如图1，当m=30°时，求∠C、∠D的度数．（3）如图2，求∠C、∠D的度数（用含m的代数式表示）．8．（1）如图（1），EF⊥GF，垂足为F，∠AEF=150°，∠DGF=60°．试判断AB和CD的位置关系，并说明理由．（2）如图（2），AB∥DE，∠ABC=70°，∠CDE=147°，∠C=．（直接给出答案）（3）如图（3），CD∥BE，则∠2+∠3﹣∠1=．（直接给出答案）（4）如图（4），AB∥CD，∠ABE=∠DCF，求证：BE∥CF．9．如图1，点E在直线BH、DC之间，点A为BH上一点，且AE⊥CE，∠DCE﹣∠HAE=90°．（1）求证：BH∥CD．（2）如图2：直线AF交DC于F，AM平分∠EAF，AN平分∠BAE．试探究∠MAN，∠AFG的数量关系．10.平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等，如图，一束光线m先射到平面镜a上，被平面镜a反射到平面镜b上，又被平面镜b反射出光线n．（1）若m∥n，且∠1=50°，则∠2=°，∠3=°；（2）若m∥n，且∠1=40°，则∠3=°；（3）根据（1）、（2）猜想：当两平面镜a、b的夹角∠3是多少度时，总有m∥n？试证明你的猜想．初一数学相交线和平行线探究题1．AB∥CD，点C在点D的右侧，∠ABC，∠ADC的平分线交于点E（不与B，D点重合）．∠ABC=n°，∠ADC=80°．（1）若点B在点A的左侧，求∠BED的度数（用含n的代数式表示）；（2）将（1）中的线段BC沿DC方向平移，当点B移动到点A右侧时，请画出图形并判断∠BED的度数是否改变．若改变，请求出∠BED的度数（用含n的代数式表示）；若不变，请说明理由．2．已知：如图①、②，解答下面各题：（1）图①中，∠AOB=55°，点P在∠AOB内部，过点P作PE⊥OA，PF⊥OB，垂足分别为E、F，求∠EPF 的度数。

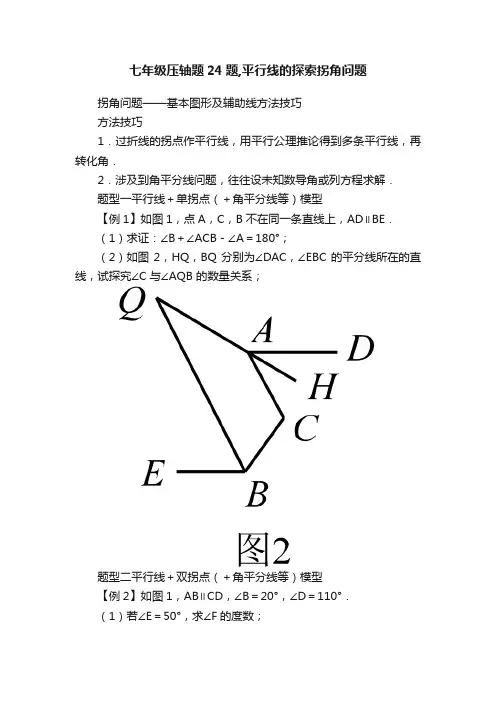
七年级压轴题24题,平行线的探索拐角问题拐角问题——基本图形及辅助线方法技巧方法技巧1．过折线的拐点作平行线，用平行公理推论得到多条平行线，再转化角．2．涉及到角平分线问题，往往设未知数导角或列方程求解．题型一平行线＋单拐点（＋角平分线等）模型【例1】如图1，点A，C，B不在同一条直线上，AD∥BE．（1）求证：∠B＋∠ACB－∠A＝180°；（2）如图2，HQ，BQ分别为∠DAC，∠EBC的平分线所在的直线，试探究∠C与∠AQB 的数量关系；题型二平行线＋双拐点（＋角平分线等）模型【例2】如图1，AB∥CD，∠B＝20°，∠D＝110°．（1）若∠E＝50°，求∠F的度数；【解答】分别过点E，F作EM∥AB，FN∥AB．∴EM∥AB∥FN．∴∠B＝∠BEM＝20°，∠MEF＝∠EFN．又∵AB∥CD，AB∥FN．∴CD∥FN．∴∠D＋∠DFN＝180°，又∵∠D＝110°，∴∠DFN ＝＝70°，易得∠EFN＝∠MEF＝∠BEF－∠BEM ＝50°－20°＝30°．∴∠EFD＝∠EFN＋∠NIFD＝30°＋70°＝100°．（2）如图2，探索∠E与∠F之间满足的数量关系，并说明理由；．【解答】分别过点E，F作EM∥AB，FN∥A B．∴EM∥AB∥FN．∴∠B＝∠BEM＝20°，∠MEF＝∠EFN，又∵AB∥CD，AB∥FN，∴CD∥FN．∴∠D＋∠DFN＝180°，又∵∠D＝110°，∴∠DFN＝70°，∴∠BEF＝∠MEF＋20°，∠EFD＝∠EFN＋70°，∴∠EFD＝∠MEF＋70°，∴∠EFD＝∠BEF＋50°．（3）如图3，EP平分∠BEF，FG平分∠EFD，FG的反向延长线交EP于点P，求∠P的度数．【分析】过点F作FH∥EP，结合（2）中结论，运用模型求解．【解答】过点F作FH∥EP，由（2）知，∠EFD＝∠BEF＋50°，设∠BEF＝2x°，则∠EFD＝(2x＋50)°，∵EP平分∠BEF，GF平分∠EFD，∴∠PEF ＝21∠BEF ＝x °，∠EFG ＝21∠EFD ＝(x ＋25)°，∵FH ∥EP ，∴∠PEF ＝∠EFH ＝x °，∠P ＝∠HFG ，∵∠HFG ＝∠EFG －∠EFH ＝25°，∴∠P ＝25°．针对练习51．如图，CD ∥BE ，则∠2＋∠3－∠1的度数等于（）A ．90°B ．120°C ．150°D ．180°2．如图，AB ∥DE ，∠C ：∠D ：∠B ＝2：3：4，则∠B ＝．3．如图，直线l 3，l 4与l 1，l 2分别相交于点A ，B ，C ，D ，且∠1＋∠2＝180°．（1）直线l 1与l 2平行吗？为什么？（2）点E 在线段AD 上，若∠ABE ＝30°，∠BEC ＝62°，求∠DCE 的度数．【解答】（1）直线l 1与l 2平行．理由如下：∵∠1＋∠BAE ＝180°，∠1＋∠2＝180°，∴∠2＝∠BAE ．∴l 1∥l 2．（2）过点E作EF∥AB交BC于点F，可得∠BEF＝∠ABE＝30°．∴∠FEC＝62°－30°＝32°．∵l1∥l2，∴EF∥CD，∴∠DCE＝∠FEC＝32°．5．将北斗七星分别标为A，B，C，D，E，F，G，如图，将A，B，C，D，E，F顺次首尾连结，若AF恰好经过点G，且AF∥DE，∠B ＝∠BCD＋10°，∠CDE＝∠E＝105°．（1）求∠F的度数；（2）计算∠B－∠CGF的度数是；（直接写出结果）（3）连接AD，∠ADE与∠CGF满足怎样数量关系时，BC∥AD？并说明理由．【解答】（1）∵AF∥DE，∴∠F＋∠E＝180°．∴∠F＝180°－105°＝75°．（2）作MC∥AF．∵AF∥DE，∴AF∥CM∥DE，∴∠BCM＝∠FGC，∠MCD＝∠CDE，∴∠BCD＝∠BCM＋∠MCD＝∠CGF＋∠CDE，∠B－∠CGF＝∠BCD＋10°－∠CGF＝∠CGF＋∠CDE＋10°－∠CGF＝∠CDE＋10°＝115°．（3）当∠ADE＋∠CGF＝180°时，BC∥A D．理由如下：∵AF∥DE，∴∠GAD＋∠ADE＝180°，∠ADE＋∠CGF＝180"．∴∠GAD＝∠CGF．∴BC∥A D．整体思想求角题型一设单个未知数求定角方法技巧巧设题目未知数，用该未知数表示其它未知角，然后运用角的和或差计算出定角【例1】如图1，直线MN 与直线AB ，CD 分别交于点E ，F ，AB ∥CD ，∠BEF 与∠EFD 的角平分线交于点P ，EP 的延长线与CD 交于点G ，点H 是MN 上一点，且CH ⊥EC ．（1）求证：PF ∥GH ；（2）如图2，连接PH ，K 是GH 上一点，∠PHK =∠HPK ，作PQ 平分∠EPK ，问∠HPQ 的大小是否发生变化？若不变，请求出其值；若变化，请说明理由图1图2【分析】（1）过点P 作AB 的平行线交MN 于点T ，运用平行线+拐点模型求∠EPF ，再根据∠ECH 的大小关系求解；（2）设∠PHK =∠HPK =x ，用x 表示未知角，运用整体思想求解。

浙教版2022年七年级数学下册第1章平行线平行线练习(含答案)第1章平行线1．1平行线知识点1平行线的概念在同一个平面内，不相交的两条直线叫做平行线．“平行”用符号“∥”表示，直线a和b是平行线，记做a∥b，读做“a平行b”．平行线的定义包含三层意思：(1)“在同一平面内”是前提条件；(2)“不相交”就是说两条直线没有交点；(3)平行线指的是“两条直线”，而不是“两条射线”或“两条线段”．1．下列说法正确的是()A．在同一平面内，不相交的两条线段是平行线段B．不相交的两条直线是平行线C．在同一平面内，不重合的两条直线的位置关系只有相交和平行两种D．在同一平面内，不相交的两条射线是平行线知识点2平行线的画法用三角尺和直尺画平行线．如图1－1－1所示，把三角尺的一边紧靠直线CD，用直尺紧靠三角板尺的另一边，沿直尺推动三角尺，然后过三角尺的一边画直线AB，这时就可画出CD的平行线AB.图1－1－12．如图1－1－2所示，过三角形ABC的三个顶点分别作它对边的平行线，标出交点，并将平行线用“∥”符号表示出来．图1－1－2知识点3平行线的性质过直线外一点只能画一条已知直线的平行线，过直线上一点不能画已知直线的平行线．3．先在纸上画三角形ABC，再任取一点P，过点P画一条直线与BC 平行，则这样的直线()A．有且只有一条B．有两条C．不存在D．有一条或不存在一利用平行线的性质进行简单的推理教材例题变式题在同一平面内，已知直线AB∥EF，直线CD与AB相交于点P，试问直线CD与EF相交吗？为什么？[归纳总结]由本题可以得出一个常用的结论：在同一平面内，如果一条直线与一组平行线中的一条相交，那么它必定与其余的直线都相交．二平面内直线交点个数的探究教材补充题已知平面内有三条互不重合的直线，请画图探究它们的位置关系并说出它们的交点个数．[反思]判断下列说法是否正确，并说明理由．(1)不相交的两条直线叫做平行线；(2)过一点有且只有一条直线与已知直线平行．一、选择题1．在同一平面内两条不重合直线的位置关系有()A．两种：平行或相交23B．两种：平行或垂直C．三种：平行、垂直或相交D．两种：垂直或相交2．如图1－1－3，在同一平面内，过点C作线段AB的平行线，下列说法正确的是()图1－1－3A．不能作B．只能作一条C．能作两条D．能作无数条3．下列关于平行的表示方法正确的是()A．a∥AB．AB∥cdC．A∥BD．a∥b4．下列四边形中，AB与CD不平行的是()图1－1－5．在同一平面内，有三条互不重合的直线，其中只有两条是平行的，那么交点有()A．0个B．1个C．2个D．3个6．下列结论正确的是()A．不相交的直线互相平行B．不相交的线段互相平行C．不相交的射线互相平行D．有公共点的直线一定不平行7．已知直线a，b在同一平面内且不相交，直线c也在这一平面内，且c与a相交，则()A．b与c相交B．b与c平行C．b与c平行或相交D．b与c的位置关系不确定二、填空题8．如图1－1－5所示，AE∥BC，AF∥BC，则A，E，F三点________，理由是____________________．图1－1－59．把图1－1－6中互相平行的线段一一写出来：______________________________________．4图1－1－610．列举现实生活中体现平行的一个例子：________.11．在同一平面内，有两条直线l1与l2.(1)若l1与l2没有公共点，则l1与l2________；(2)若l1与l2有且只有一个公共点，则l1与l2________；(3)若l1与l2有两个公共点，则l1与l2________．三、解答题12．如图1－1－7，在长方体中，A1B1∥AB，AD∥BC，你能找出图中的平行线吗？图1－1－713．如图1－1－8所示，点P在∠AOB的一边OA上，点Q在∠AOB的另一边OB上，按下列要求画图：(1)过点P，Q的直线；(2)过点P画平行于OB的直线；(3)过点Q画平行于OA的直线．图1－1－814．如图1－1－9，点P是∠ABC内一点．(1)过点P画一条直线平行于直线AB，且与BC交于点D；(2)过点P画一条直线垂直于直线BC，垂足为E；(3)过点P作直线AB的垂线段PF.图1－1－91．[实践操作题]如图1－1－10所示，D，E是线段AC的三等分点．(1)过点D作DF∥BC交AB于点F，过点E作EG∥BC交AB于点G；(2)量出AF，FG，GB的长度(精确到0.1cm)，你有什么发现？(3)量出FD，GE，BC的长度(精确到0.1cm)，你有什么发现？(4)根据(3)中发现的规律，若FD＝1.5cm，则EG＝________cm，BC＝________cm.图1－1－102.[操作探究]我们知道在同一平面内，两条平行直线的交点有0个，两条相交直线的交点有1个，平面内三条平行直线的交点有0个，经过同一点的三条直线的交点有1个……(1)平面上有三条互不重合的直线，请画图探究它们的交点个数；(2)若平面内的五条直线恰有4个交点，请画出符合条件的所有图形；(3)在平面内画出10条直线，使它们的交点个数恰好是32.详解详析5【预习效果检测】1．[解析]C根据平行线的概念“在同一平面内，不相交的两条直线叫做平行线”即可得出答案．[点评]正确理解平行线的概念是解决本题的关键．学习此概念时，我们要特别注意“在同一平面内”“不相交”“直线”等关键词．2．解：如图所示．过点A作BC边的平行线，过点B作AC边的平行线，过点C作AB边的平行线，两两相交于点D，E，F，所以DE∥BC，EF∥AC，DF∥AB.3．[解析]D当点P在直线BC外时，根据“经过直线外一点，有且只有一条直线与这条直线平行”这个基本事实，可知有且仅有一条；但当点P在直线BC上时，就不存在这样的直线，故本题应选择D.【重难互动探究】例1[解析]由于直线AB，EF的位置关系已确定，AB与CD的位置关系也确定了，根据平行线的性质即可确定CD与EF的位置关系．解：直线CD与EF相交．因为AB∥EF，CD与AB相交于点P，而过点P只能作一条直线AB与EF平行，所以直线CD与EF相交．例2[解析]在同一平面内，两条不重合直线的位置关系只有两种：相交和平行．若在同一平面内有三条或三条以上直线，其位置关系就变得比较复杂，交点个数也不确定，因此需分类讨论进行探究．解：①如图①，三条直线互相平行，此时交点个数为0；②如图②，三条直线相交于一点，此时交点个数为1；③如图③，三条直线两两相交且不交于同一点，此时交点个数为3；④如图④，其中两条直线互相平行且都与第三条直线相交，此时交点个数为2.【课堂总结反思】[反思](1)不正确，理由：在同一平面内，不相交的两条直线叫做平行线．(2)不正确，理由：过直线外一点，有且只有一条直线与这条直线平行；过直线上一点，不能画已知直线的平行线．【作业高效训练】[课堂达标]1．A2.B3.D4.D5.C6.D7.A68．[答案]共线经过直线外一点，有且只有一条直线与这条直线平行9．[答案]GH∥MN，EF∥AB，CD∥PQ10．[答案]如双杠．两条笔直的铁轨等(答案不唯一，写出一个即可) 11．[答案](1)平行(2)相交(3)重合12．解：图中的平行线有AB∥DC∥D1C1∥A1B1，AD∥BC∥B1C1∥A1D1，AA1∥BB1∥CC1∥D D1.13．[解析]借助三角尺和直尺画平行线．用三角尺和直尺画图，其基本步骤如下：一落：三角尺的一边落在已知直线上；二靠：紧靠三角尺其余两边中的任意一边放上直尺；三移：三角尺沿直尺移动，使三角板尺的边经过已知点；四画：沿三角尺过已知点的一边画直线．解：如图所示．14．解：如图所示．[数学活动]1．解：(1)如图所示．(2)测量略，AF＝FG＝GB.(3)测量略，FD∶GE∶BC＝1∶2∶3或FD＋BC＝2GE.(4)34.52．解：(1)如图所示．(2)如图所示．(3)如图所示．78。

浙教版七年级下册数学第一章平行线含答案一、单选题(共15题，共计45分)1、在学习“用直尺和三角板画平行线”的时候，课本给出如图的画法，这种画平行线方法的依据是（）A.内错角相等，两直线平行B.同位角相等，两直线平行C.两直线平行，内错角相等D.两直线平行，同位角相等2、如图，已知AD∥BC，∠B=32°，DB平分∠ADE，则∠DEC=（）A.64°B.66°C.74°D.86°3、如图，已知AB∥CD，直线MN分别交AB、CD于点M、N，NG平分∠MND，若∠1=70°，则∠2的度数为（）A.10°B.15°C.20°D.35°4、已知∠1和∠2是同旁内角，∠1=40°，∠2等于（）A.160°B.140°C.40°D.无法确定5、如图，AB⊥AC，CD、BE分别是△ABC的角平分线，AG∥BC，AG⊥BG，下列结论：①∠BAG＝2∠ABF；②BA平分∠CBG；③∠ABG＝∠ACB；④∠CFB＝135°，其中正确的结论有（）个A.1B.2C.3D.46、下列四个命题中，真命题有（）两条直线被第三条直线所截，内错角相等；如果和是对顶角，那么；三角形的一个外角大于任何一个内角；若，则.A.1个B.2个C.3个D.4个7、如图，是的直径，，是上的两点，且平分，分别与，相交于点，，则下列结论不一定成立的是（）A. B. C. D.8、如图，AB∥CD，∠ABE=60°，∠D=50°，则∠E的度数为（）A.30°B.20°C.10°D.40°9、下列四个命题中，其正确命题的个数是（）①若ac＞bc，则a＞b；②平分弦的直径垂直于弦；③一组对角相等一组对边平行的四边形是平行四边形；④反比例函数y＝．当k＜0时，y随x的增大而增大A.1B.2C.3D.410、下列说法错误的是（）A.经过平移，对应点所连的线段平行且相等B.经过平移，对应线段平行C.平移中，图形上每个点移动的距离可以不同D.平移不改变图形的形状和大小11、如图，直线l1∥l2，∠1=55°，∠2=65°，则∠3为（）A.50°B.55°C.60°D.65°12、如图，在△ABC中，点D是线段AB的中点，DC⊥BC，作∠EAB＝∠B，DE∥BC，连接CE.若，设△BCD的面积为S，则用S表示△ACE的面积正确的是（）A. B.3S C.4S D.13、如图，直线a，b被直线c所截，下列条件中，不能判定a∥b（）A.∠2=∠4B.∠1+∠4=180°C.∠5=∠4D.∠1=∠314、如图，已知AB∥CD，∠B=60°，则∠1的度数是（）A.60°B.100°C.110°D.120°15、如图，下列不能判定DF∥AC的条件是（）A.∠A＝∠BDFB.∠2＝∠4C.∠1＝∠3D.∠A+∠ADF＝180°二、填空题(共10题，共计30分)16、完成下面的证明：已知：如图，AB∥DE，求证：∠D+∠BCD-∠B=180°，证明：过点C作CF∥AB．∵AB∥CF（已知），∴∠B=________ ( 依据：________)．∵AB∥DE，CF∥AB( 已知 ) ，∴CF∥DE (依据：________)∴∠2+________=180°( 依据：________)∵∠2=∠BCD -∠1，∴∠D+∠BCD-∠B=180°．17、如图，a∥b，∠2=100°，则∠1的度数为________．18、如图，△AOB与△ACD均为正三角形，且顶点B、D均在双曲线y= （x＞0）上，点A、C在x轴上，连接BC交AD于点P，则△OBP的面积=________．19、如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3=________°．20、如图，直线a、b被第三条直线c所截，如果a∥b,∠1=50°,那么∠2=________。

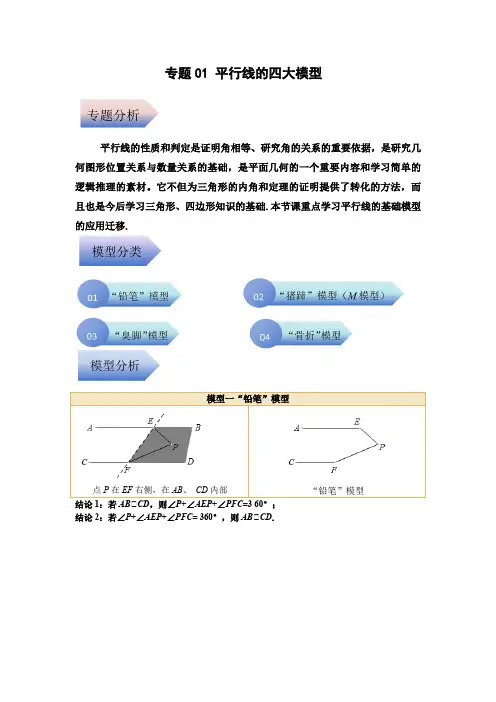
专题01 平行线的四大模型平行线的性质和判定是证明角相等、研究角的关系的重要依据，是研究几何图形位置关系与数量关系的基础，是平面几何的一个重要内容和学习简单的逻辑推理的素材。

它不但为三角形的内角和定理的证明提供了转化的方法，而且也是今后学习三角形、四边形知识的基础.本节课重点学习平行线的基础模型的应用迁移.模型一“铅笔”模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°；结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.专题分析模型分类模型分析【典例1】（2023秋•南岗区校级期中）已知，射线FG分别交射线AB、DC于点F、G，点E为射线FG上一点．（1）如图1，若∠A+∠D＝∠AED，求证：AB∥CD．（2）如图2，若AB∥CD，求证：∠A﹣∠D＝∠AED．（3）如图3，在（2）的条件下，DI交AI于点Ⅰ，交AE于点K，∠EDI＝∠CDE，∠BAI＝∠EAI，∠I＝∠AED＝25°，求∠EKD的度数．【变式1-1】（2023•渝中区校级模拟）如图，已知直线a∥b，∠BAC＝90°，∠1＝40°，则∠2的度数为（）A．40°B．50°C．130°D．140°典例分析【变式1-2】（2023•金安区一模）如图，已知a∥b，∠1＝45°，∠2＝125°，则∠ABC的度数为（）A．100°B．105°C．115°D．125°【变式1-3】（2022春•肇州县期末）如图，AB∥CD，∠C＝110°，∠B＝120°，则∠BEC ＝（）A．110°B．120°C．130°D．150°【变式1-4】（2023春•巴南区月考）已知直线MN∥PQ，点C、B分别在直线MN、PQ上，点A在直线MN和PO之间．（1）如图1，求证：∠CAB﹣∠MCA＝∠PBA；（2）如图2，CD∥AB，点E在直线PQ上，且∠MCA＝∠DCE，求证：∠ECN＝∠CAB；（3）如图3，BF平分∠PBA，CG平分∠ACN，且AF∥CG．若∠CAB＝50°，直接写出∠AFB的度数．【变式1-5】（2023春•遂宁期末）如图，直线PQ∥MN，两个三角形如图①放置，其中∠ABC ＝∠CDE＝90°，∠ACB＝30°，∠BAC＝60°，∠DCE＝∠DEC＝45°，点E在直线PQ上，点B，C均在直线MN上，且CE平分∠ACN．（1）求∠DEQ的度数；（2）如图②，若将△ABC绕B点以每秒3°的速度按逆时针方向旋转（A，C的对应点分别为F，G）．设旋转时间为t秒，当t＝10时，边BG与CD有何位置关系？请说明理由．模型分析模型二“猪蹄”模型（模型）点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.典例分析【典例2】（2023春•邵阳县期末）如图，直线AB∥CD，连接EF，直线AB，CD及线段EF 把平面分成①②③④四个部分，规定：线上各点不属于任何部分．当动点G落在某个部分时，连接GE，GF，构成∠EGF，∠GEB，∠GFD三个角．（1）当动点G落在第③部分时，如图一，试说明：∠EGF，∠GEB，∠GFD三者的关系；（2）当动点G落在第②部分时，如图二，思考（1）中三者关系是否仍然成立若不成立，说明理由．【变式2-1】（2023•盘锦）如图，直线AB∥CD，将一个含60°角的直角三角尺EGF按图中方式放置，点E在AB上，边GF，EF分别交CD于点H，K，若∠BEF＝64°，则∠GHC等于（）A．44°B．34°C．24°D．14°【变式2-2】（2023•盘锦）如图，直线AB∥CD，将一个含60°角的直角三角尺EGF按图中方式放置，点E在AB上，边GF，EF分别交CD于点H，K，若∠BEF＝64°，则∠GHC等于（）A．44°B．34°C．24°D．14°【变式2-3】（2023•海南模拟）如图，已知AB∥DE，∠B＝20°，∠D＝130°，那么∠BCD 等于（）A．60°B．70°C．80°D．90°【变式2-4】（2023春•覃塘区期末）如图，AB∥CD，将一副直角三角板作如下摆放，∠GEF ＝60°，∠MNP＝45°．下列结论：①GE∥MP；②∠EFN＝150°；③∠BEF＝65°；④∠AEG＝35°，其中正确的个数是（）A．1B．2C．3D．4【变式2-5】（2023春•赣县区期末）【问题背景】：同学们，观察小猪的猪蹄，你会发现一个熟悉的几何图形，我们就把这个图形的形象称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系．【问题探究】：（1）如图1，AB∥CD，E为AB、CD之间一点，连接BE、DE，得到∠BED 与∠B、∠D之间的数量关系，并说明理由；【类比迁移】：（2）请你利用上述“猪蹄模型”得到的结论或解题方法，完成下面的问题：如图2，直线AB∥CD，若∠B＝23°，∠G＝35°，∠D＝25°，求∠BEG+∠GFD的度数；【灵活应用】：（3）如图3，直线AB∥CD，若∠E＝∠B＝60°，∠F＝85°，则∠D＝25度．【变式2-6】（2023春•邵阳期末）如图1，直线AB∥CD，P是截线MN上的一点．（1）若∠MNB＝45°，∠MDP＝20°，求∠MPD；（2）如图1，当点P在线段MN上运动时，∠CDP与∠ABP的平分线交于Q，问是否为定值，若是定值，请求出；若不是定值，请说明理由；（3）如图2，若T是直线MN上且位于M点的上方的一点，如图所示，当点P在射线MT上运动时，∠CDP与∠ABP的平分线交于Q，问的值是否和（2）问中的情况一样呢？请你写出探究过程，说明理由．【变式2-7】（2023春•防城港期末）阅读下面材料：（1）小亮同学遇到这样一个问题：已知：如图甲，AB∥CD，E为直线AB，CD之间一点，连接BE、DE得到∠BED．求证：∠BED＝∠B+∠D．下面是小亮写出了该问题的证明，请你帮他把证明过程补充完整．证明：过点E作EF∥AB，则有∠BEF＝∠B，∵AB∥CD，∴CD∥EF，∴∠FED＝∠D，∴∠BED＝∠BEF+∠FED＝∠B+∠D．（2）请你参考小亮思考问题的方法，解决问题：如图乙，直线a∥b，BE平分∠ABC，DE平分∠ADC，若∠ABC＝50°，∠ADC＝60°，求∠BED的度数，（温馨提示：过点E作EF∥AB）模型分析模型三“臭脚”模型“臭脚”模型结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.典例分析【典例3】（2023春•中山区期末）如图，∠ABE+∠BED＝∠CDE．（1）如图1，求证AB∥CD；（2）如图2，点P在AB上，∠CDP＝∠EDP，BF平分∠ABE，交PD于点F，探究∠BFP，∠BED的数量关系，并证明你的结论；（3）在（2）的条件下，如图3，PQ交ED延长线于点Q，∠DPQ＝2∠APQ，∠PQD ＝80°，求∠CDE的度数．【变式3-1】已知AB∥CD．（1）如图1，求证：∠ABE+∠DCE﹣∠BEC＝180°；（2）如图2，∠DCE的平分线CG的反向延长线交∠ABE的平分线BF于F．若BF∥CE，∠BEC＝26°，求∠BFC．模型分析结论1：若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.典例分析【典例4】（2022秋•朝阳区校级期末）已知AB∥CD，点E在AB上，点F在DC上，点G 为射线EF上一点．（1）【基础问题】如图1，试说明：∠AGD＝∠A+∠D．（完成图中的填空部分）证明：过点G作直线MN∥AB，又∵AB∥CD，∴∥CD∵MN∥AB，∴∠＝∠MGA．∵MN∥CD，∴∠D＝（）∴∠AGD＝∠AGM+∠DGM＝∠A+∠D．（2）【类比探究】如图2，当点G在线段EF延长线上时，请写出∠AGD、∠A、∠D三者之间的数量关系，并说明理由．（3）【应用拓展】如图3，AH平分∠GAE，DH交AH于点H，且∠GDH＝2∠HDF，∠HDF＝22°，∠H＝32°，直接写出∠DGA的度数为°．【变式4-1】（2022秋•肃州区校级期末）如图（1），AB∥CD，∠AEP＝40°，∠PFD＝130°，求∠EPF的度数．小明想到了以下方法：解：如图（1），过点P作PM∥AB，∴∠1＝∠AEP＝40°（两直线平行，内错角相等）∵AB∥CD（已知）∴PM∥CD（平行于同一条直线的两直线平行）∴∠2+∠PFD＝180°（两直线平行，同旁内角互补）∵∠PFD＝130°（已知）∴∠2＝180°﹣130°＝50°∴∠EPF＝∠1+∠2＝40°+50°＝90°即∠EPF＝90°【探究】如图（2），AB∥CD，∠AEP＝50°，∠PFC＝120°，求∠EPF的度数．【应用】如图（3），在【探究】的条件下，∠PEA的平分线和∠PFC的平分线交于点G，求∠G的度数．【变式4-2】（2022春•朝阳县期末）学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．（1）小明遇到了下面的问题：如图1，l1∥l2，点P在l1，l2内部，探究∠A，∠APB，∠B的关系，小明过点P作l1的平行线，可得∠APB，∠A，∠B之间的数量关系是：∠APB＝．（2）如图2，若AC∥BD，点P在AC，BD外部，∠A，∠B，∠APB的数量关系是否发生变化？请写出证明过程．【变式4-3】（2020春•乳山市期中）【信息阅读】材料信息：如图①，AB∥DE，点C是直线AB，DE外任意一点，连接BC，DC．方法信息：如图②，在“材料信息”的条件下，∠B＝55°，∠D＝35°，求∠BCD的度数．解：过点C作CF∥AB．∴∠BCF＝∠B＝55°．∵AB∥DE，∴CF∥DE．∴∠DCF＝∠D＝35°．∴∠BCD＝55°﹣35°＝20°．【问题解决】（1）通过【信息阅读】，猜想：∠B，∠D，∠BCD之间有怎样的等量关系？请直接写出结论：；（2）如图③，在“材料信息”的条件下，改变点C的位置，∠B，∠D，∠BCD之间的等量关系是否改变？若不改变，请写出理由；若改变，请写出新的等量关系及理由．1.（2023春•建昌县期末）如图，将一个含30°角的直角三角板的直角顶点C放在直尺的两边MN，PQ之间，则下列结论中：①∠1＝∠3；②∠2＝∠3；③∠1+∠3＝90°；④若∠3＝60°，则AB⊥PQ，其中正确结论的个数是（）A．1个B．2个C．3个D．4个2．（2023春•芜湖期末）如图所示是汽车灯的剖面图，从位于O点灯发出光照射到凹面镜上反射出的光线BA，CD都是水平线，若∠ABO＝α，∠DCO＝60°，则∠BOC的度数为（）A．180°﹣αB．120°﹣αC．60°+αD．60°﹣α3．（2022•恩施州）已知直线l1∥l2，将含30°角的直角三角板按如图所示摆放．若∠1＝120°，则∠2＝（）A．120°B．130°C．140°D．150°4．（2022•博山区一模）如图，直线a∥b，点M、N分别在直线a、b上，P为两平行线间一点，那么∠1+∠2+∠3等于（）A．360°B．300°C．270°D．180°5．（2021春•椒江区校级月考）如图，已知AB∥CD，∠BAD和∠BCD的平分线交于点E，∠FBC＝n°，∠BAD＝m°，则∠AEC等于（）度．A．90﹣+m B．90﹣﹣C．90﹣D．90﹣+ 6．（2023春•赫山区期末）【问题情景】（1）如图1，AB∥CD，∠P AB＝135°，∠PCD＝115°，求∠APC的度数；【问题迁移】（2）如图2，已知∠MON，AD∥BC，点P在射线OM上运动，当点P在A，B两点之间运动时，连接PD，PC，∠ADP＝∠α，∠BCP＝∠β，求∠CPD与∠α，∠β之间的数量关系，并说明理由；【知识拓展】（3）在（2）的条件下，若将“点P在A，B两点之间运动”改为“点P在A，B两点外侧运动（点P与点A，B，O三点不重合）”其他条件不变，请直接写出∠CPD 与∠α，∠β之间的数量关系．7．（2022春•良庆区校级期中）已知AM∥CN，点B为平面内一点，AB⊥BC于B．（1）如图1，直接写出∠A和∠C之间的数量关系；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD＝∠C；（3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB＝∠CFD，∠BFC＝3∠DBE，求∠EBC的度数．8．（2021秋•平昌县期末）如图，AD∥BC，∠BAD的平分线交BC于点G，∠BCD＝90°．（1）试说明：∠BAG＝∠BGA；（2）如图1，点F在AG的反向延长线上，连接CF交AD于点E，若∠BAG﹣∠F＝45°，求证：CF平分∠BCD．（3）如图2，线段AG上有点P，满足∠ABP＝3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM＝∠DCH，求的值．9．（2023春•黑山县期中）问题情境我们知道，“两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补”，所以在某些探究性问题中通过“构造平行线”可以起到转化的作用．已知三角板ABC中，∠BAC＝60°，∠B＝30°，∠C＝90°，长方形DEFG中，DE∥GF．问题初探（1）如图（1），若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点N，求∠EMC的度数．分析：过点C作CH∥GF．则有CH∥DE，从而得∠CAF＝∠HCA，∠EMC＝∠MCH，从而可以求得∠EMC的度数．由分析得，请你直接写出：∠CAF的度数为，∠EMC的度数为．类比再探（2）若将三角板ABC按图（2）所示方式摆放（AB与DE不垂直），请你猜想写∠CAF 与∠EMC的数量关系，并说明理由．（3）请你总结（1），（2）解决问题的思路，在图（3）中探究∠BAG与∠BMD的数量关系？并说明理由．10．（2022春•龙亭区校级期末）如图，已知AB∥CD，E、F分别在AB、CD上，点G在AB、CD之间，连接GE、GF．（1）当∠BEG＝40°，EP平分∠BEG，FP平分∠DFG时：①如图1，若EG⊥FG，则∠P的度数为；②如图2，在CD的下方有一点Q，EG平分∠BEQ，FD平分∠GFQ，求∠Q+2∠P的度数；（2）如图3，在AB的上方有一点O，若FO平分∠GFC．线段GE的延长线平分∠OEA，则当∠EOF+∠EGF＝100°时，请直接写出∠OEA与∠OFC的数量关系．11．（2023春•孝义市期末）综合与探究数学活动课上，老师以“一个含45°的直角三角板和两条平行线”为背景展开探究活动，如图1，已知直线m∥n，直角三角板ABC中，∠ACB＝90°，∠BAC＝∠ABC＝45°．（1）如图1，若∠2＝65°，则∠1＝；（直接写出答案）（2）“启航”小组在图1的基础上继续展开探究：如图2，调整三角板的位置，当三角板ABC的直角顶点C在直线n上，直线m与AB，AC相交时，他们得出的结论是：∠1﹣∠2＝135°，你认为启航小组的结论是否正确，请说明理由；（3）如图3，受到“启航”小组的启发，“睿智”小组提出的问题是：在图2的基础上，继续调整三角板的位置，当点C不在直线n上，直线m与AC，BC相交时，∠1与∠2有怎样的数量关系？请你用平行线的知识说明理由．12．（2023春•安化县期末）在课后学习中，小红探究平行线中的线段与角的数量关系，如图，直线AB∥CD，点N在直线CD上，点P在直线AB上，点M为平面上任意一点，连接MP，MN，PN．（1）如图1，点M在直线CD上，PM平分∠APN，试说明∠PMN＝∠MPN；（2）如图2，点M在直线AB，CD之间，∠PMN＝70°，∠MNC＝30°，求∠APM的度数；（3）如图3，∠APM和∠MNC的平分线交于点Q，∠PQN与∠PMN有何数量关系？并说明理由．12．（2023春•甘井子区期末）如图1，点M在射线BA，CD之间，0°＜∠ABM＜30°，连接BM，过点M作ME⊥BM交射线CD于点E，且∠MED﹣∠B＝90°．（1）求证：AB∥CD；（2）过点C作∠ECN＝∠B，交直线ME于点N，先按要求画图，再解决下列问题．①当CN在CD上方，满足∠CNE＝5∠B时，在图2中画图，求∠B的度数；②作∠BME的角平分线交射线CD于点K，交∠ECN的角平分线于点F，请直接写出∠MKC与∠MFC之间的数量关系．。

第五章《相交线与平行线》期末复习讲义5.2平行线及其判定【知识回顾】一．平行线1.定义：在同一平面内，__________的两条直线叫做平行线2.要点剖析（1）：平行线的特征：在同一平面内；是直线；没有公共点。

（2）在同一平面内，不重合的两条直线的位置关系只有相交和平行两种，重合的直线视为一条直线。

（3）平行线是指的两条直线的位置关系，两条射线或线段平行，是指的它们所在的直线平行。

二．平行线的画法1.“一落”把三角尺的一边落在已知直线上2.“二靠”用直尺紧靠三角尺的另一边3.“三推”把三角尺沿着直尺推到三角尺的一边刚好过已知点的位置4.“四画”沿三角尺过已知点的边画直线三．平行公理及其推论1.平行公理：经过直线外一点，_________一条直线与这条直线平行2.平行公理的推论：如果两条直线都与_________直线平行，那么这两条直线也互相平行四．平行线的判定1.同位角相等，两直线_________2.内错角相等，两直线_________3.同旁内角互补，两直线___________4.在同一平面内，垂直于_______________的两条直线互相平行题型拓展题型1 平行公理及其推论的应用例1：1．如图，取一张长方形的硬纸板ABCD，将硬纸板ABCD对折使CD与AB重合，EF 为折痕．把长方形ABEF平放在桌面上，另一个面CDEF无论怎么改变位置，总有CD∥AB存在，你知道为什么吗？例2：2．如图，取一张长方形的硬纸片ABCD对折，MN是折痕，把ABNM平摊在桌面上，另一个面CDMN不论怎样改变位置，总有MN∥∥．因此∥．题型2 综合运用各种判定方法判定两条直线平行例1：3．如图，∠1＝47°，∠2＝133°，∠D＝47°，那么BC与DE平行吗？AB与CD呢？为什么？例2：4．阅读下面的推理过程，在括号内填上推理的依据，如图：因为∠1+∠2＝180°，∠2+∠4＝180°（已知）所以∠1＝∠4，（）所以a∥c．（）又因为∠2+∠3＝180°（已知）∠3＝∠6（）所以∠2+∠6＝180°，（）所以a∥b．（）所以b∥c．（）题型3 平行线判定的开放探究题例1：5．如图，∠A＝60°，∠1＝60°，∠2＝120°，猜想图中哪些直线平行，并证明．例2：6．如图，直线a，b被c所截，∠1＝50°，若要a∥b，则需增加条件（填图中某角的度数）；依据是．题型4 平行线的判定在实际生活中的应用例1：7．如图所示，给你两块同样的三角板和一根直尺（直尺比桌子长），请你设计一个方案，检验桌子的相对边缘线是否平行？例2：8．在铺设铁轨时，两条直轨必须是互相平行的，如图，已经知道∠2是直角，那么再度量图中已标出的哪个角，就可以判断两条直线是否平行？为什么？课后提高训练9．下列说法错误的是（）A．平行于同一条直线的两直线平行B．两直线平行，同旁内角互补C．对顶角相等D．同位角相等10．如图，下面哪个条件不能判断AC∥EF的是（）A．∠1＝∠2B．∠4＝∠C C．∠1+∠3＝180°D．∠3+∠C＝180°11．如图，平面内有五条直线l1、l2、l3、l4、l5，根据所标角度，下列说法正确的是（）A．l1∥l2B．l2∥l3C．l1∥l3D．l4∥l512．如图，在下列条件中，能判断AB∥CD的是（）A．∠1＝∠4B．∠BAD＝∠BCDC．∠BAD+∠ADC＝180°D．∠2＝∠313．如图所示，下列推理正确的是（）A．∵∠1＝∠4（已知）∴AB∥CD（内错角相等，两直线平行）B．∵∠2＝∠3（已知）∴AE∥DF（内错角相等，两直线平行）C．∵∠1＝∠3（已知）∴AB∥DF（内错角相等，两直线平行）D．∵∠2＝∠2（已知）∴AE∥DC（内错角相等，两直线平行）14．下列说法中正确的个数为（）①过一点有且只有一条直线与已知直线垂直②两条直线被第三条直线所截，同位角相等③经过两点有一条直线，并且只有一条直线④在同一平面内，不重合的两条直线不是平行就是相交A．1个B．2个C．3个D．4个15．如图，下列能判定AB∥CD的条件有（填序号）①∠B+∠BCD＝180°；②∠2＝∠3；③∠1＝∠4；④∠B＝∠5；⑤∠D＝∠5．16．如图，要使BE∥DF，需补充一个条件，你认为这个条件应该是（填一个条件即可）．17．一副三角板按如图所示叠放在一起，其中点C、D重合，若固三角板定ABC，改变三角板AED的位置（其中A点位置始终不变），当∠CAD＝时，ED∥AC．18．如图，直线a、b被直线c所截，现给出的下列四个条件：①∠4＝∠7；②∠2＝∠5；③∠2+∠3＝180°；④∠2＝∠7．其中能判定a∥b的条件的序号是．19．已知：∠A＝∠C＝120°，∠AEF＝∠CEF＝60°，求证：AB∥CD．20．如图，若∠1＝42°，∠2＝53°，∠3＝85°，则直线l1与l2平行吗？判断并说明理由．21．如图，已知CD⊥AD于点D，DA⊥AB于点A，∠1＝∠2，试说明DF∥AE．解：因为CD⊥AD（已知），所以∠CDA＝90°（）．同理∠DAB＝90°．所以∠CDA＝∠DAB＝90°（）．即∠1+∠3＝∠2+∠4＝90°．因为∠1＝∠2（已知），所以∠3＝∠4（）．所以DF∥AE（）．22．完成下列证明过程，并在括号内填上依据．如图，点E在AB上，点F在CD上，∠1＝∠2，∠B＝∠C，求证AB∥CD．证明：∵∠1＝∠2（已知），∠1＝∠4（），∴∠2＝∠4（等量代换），∴（）．∴∠3＝∠C（）．又∵∠B＝∠C（已知），∴∠3＝∠B（等量代换），∴AB∥CD（）．参考答案与解析1.解：∵四边形FECD是矩形，∴CD∥EF；又∵四边形ABEF是矩形，∴AB∥EF，∴CD∥AB．2.解：∵长方形的硬纸片ABCD对折，MN是折痕，∴MN∥AB，MN∥CD，即MN∥AB∥CD，∴AB∥CD（平行于同一直线的两条直线互相平行）．故各空依次填AB、CD、AB、CD．3.解：BC∥DE，AB∥CD．理由如下：∵∠1＝47°，∠2＝133°，而∠ABC＝∠1＝47°，∴∠ABC+∠2＝180°，∴AB∥CD；∵∠2＝133°，∴∠BCD＝180°﹣133°＝47°，而∠D＝47°，∴∠BCD＝∠D，∴BC∥DE．4.解：因为∠1+∠2＝180°，∠2+∠4＝180°（已知），所以∠1＝∠4，（同角的补角相等）所以a∥c．（内错角相等，两直线平行）又因为∠2+∠3＝180°（已知）∠3＝∠6（对顶角相等）所以∠2+∠6＝180°，（等量代换）所以a∥b．（同旁内角互补，两直线平行）所以b∥c．（平行于同一条直线的两条直线平行）．故答案为：同角的补角相等；内错角相等，两直线平行；对顶角相等；等量代换；同旁内角互补，两直线平行；平行于同一条直线的两条直线平行．5.解：如图，∵∠A＝60°，∠1＝60°，∴∠A＝∠1，∴DE∥AC．又∵∠A＝60°，∠2＝120°，∴∠A+∠2＝180°，∴EF∥AB．6.解：∵∠3＝50°，1＝50°，∴∠1＝∠3，∴a∥b（同位角相等，两直线平行）．故答案为：∠3＝50°；同位角相等；两直线平行．7.解：（1）将直尺放在桌面上，使其与桌面一组对边相交；（2）将三角板一边贴近直尺，斜边贴近桌面边缘；（3）使另一个三角形同样方法放置，如果相符合说明对边平行，原理如图所示，若∠1＝∠2则a∥b，再检查另一组对边是否平行．8.解：①通过度量∠3的度数，若满足∠2+∠3＝180°，根据同旁内角互补，两直线平行，就可以验证这个结论；②通过度量∠4的度数，若满足∠2＝∠4，根据同位角相等，两直线平行，就可以验证这个结论；③通过度量∠5的度数，若满足∠2＝∠5，根据内错角相等，两直线平行，就可以验证这个结论．9. D10.C11.D12.C13.B14.B15.解：选项①中∵∠B+∠BCD＝180°，∴AB∥CD（同旁内角互补，两直线平行），所以正确；选项②中，∵∠2＝∠3，∴AD∥BC（内错角相等，两直线平行），所以错误；选项③中，∵∠1＝∠4，∴AB∥CD（内错角相等，两直线平行），所以正确；选项④中，∵∠B＝∠5，∴AB∥CD（同位角相等，两直线平行），所以正确；选项⑤中，∠D＝∠5，∴AD∥BC（内错角相等，两直线平行），所以错误；故答案为：①③④．16.解：添加条件为：∠D＝∠COE．理由如下：∵∠D＝∠COE，∴BE∥DE（同位角相等，两直线平行）．故答案为：∠D＝∠COE（答案不唯一）．17.解：如图所示：当ED∥AC时，∠CAD＝∠D＝30°；如图所示，当ED∥AC时，∠E＝∠EAC＝60°，∴∠CAD＝60°+90°＝150°；故答案为：30°或150°．18.解：当∠4＝∠7时，a∥b，故①正确；当∠2＝∠5时，无法证明a∥b，故②错误；当∠2+∠3＝180°时，无法证明a∥b，故③错误；当∠2＝∠7时，a∥b，故④正确；故答案为：①④．19.证明：∵∠A＝∠C＝120°，∠AEF＝∠CEF＝60°，∴∠A+∠AEF＝180°，∠C+∠CEF＝180°，∴AB∥EF，CD∥EF，∴AB∥CD．20.解：直线l1与l2平行，理由：∵∠1＝∠4，∠2＝∠5，∠1＝42°，∠2＝53°，∴∠4＝42°，∠5＝53°，又∵∠3＝85°，∴∠3+∠5＝85°+53°＝138°，∴∠3+∠5+∠4＝138°+42°＝180°，∴l1∥l2（同旁内角互补，两直线平行）．21.解：因为CD⊥AD（已知），所以∠CDA＝90°（垂直的定义），同理∠DAB＝90°．所以∠CDA＝∠DAB＝90°（等量代换），即∠1+∠3＝∠2+∠4＝90°．因为∠1＝∠2（已知），所以∠3＝∠4（等式的性质1），所以DF∥AE（内错角相等，两直线平行）．22.证明：∵∠1＝∠2（已知），∠1＝∠4（对顶角相等），∴∠2＝∠4（等量代换），∴CE∥BF（同位角相等，两直线平行）．∴∠3＝∠C（两直线平行，同位角相等）．又∵∠B＝∠C（已知），∴∠3＝∠B（等量代换），∴AB∥CD（内错角相等，两直线平行）．故答案为：对顶角相等；CE∥BF；同位角相等，两直线平行；C；两直线平行，同位角相等；内错角相等，两直线平行．。

浙教版七年级下册数学第一章平行线含答案一、单选题(共15题，共计45分)1、如图，两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起，固定三角形ABC不动，将三角形DEF向右平移，当点E和点C重合时，停止平移. 连结AE，DC，在整个过程中，图中阴影部分面积和的变化情况是（）A.一直增大B.一直减少C.先减少后增大D.一直不变2、如图，已知AB∥CD，∠C=35°，BC平分∠ABE，则∠ABE的度数是( )A.17.5°B.35°C.70°D.105°3、如图，将含30°角的直角三角板ABC放在平行线α和b上，∠C＝90°，∠A＝30°，若∠1＝20°，则∠2的度数等于（）A.60°B.50°C.40°D.30°4、如图所示的四个图形中，∠1和∠2一定相等的是（）A. B. C. D.5、下列选项中∠1与∠2不是同位角的是（）A. B. C.D.6、观察图，在下列四种图形变换中，该图案不包含的变换是（）A.旋转B.轴对称C.位似D.平移7、在同一平面内，不重合的两条直线的位置关系是（）A.平行B.相交C.平行或相交D.平行、相交或垂直8、小明同学把一个含有45°角的直角三角板放在如图所示的两条平行线m、n 上，测得∠α=120°，则∠β的度数是（）A.45°B.55°C.65°D.75°9、已知：如图，点D是射线AB上一动点，连接CD，过点D作DE∥BC交直线AC于点E，若∠ABC=84°，∠CDE=20°，则∠ADC的度数为( )A.104°B.76°C.104°或64°D.104°或76°10、下列说法错误的是（）A.两直线平行，内错角相等B.两直线平行，同旁内角相等C.对顶角相等D.平行于同一条直线的两直线平行11、如图．已知直线a，b被直线c所截，且a∥b，∠1=48°，那么∠2的度数为（）A.42°B.48°C.52°D.132°12、如图，将三角形纸板ABC沿直线AB平移，使点A移到点B，若∠CAB=50°，∠ABC=100°，则∠CBE的度数为（）A.50°B.40°C.30°D.100°13、如图，己知l∥AB，AC为角平分线，下列说法错误的是（）1A.∠1=∠4B.∠1=∠5C.∠2=∠3D.∠1=∠314、如图，两个全等的直角三角形重叠在一起，将其中沿着点B到C的方向平移到的位置，，平移距离为，则的面积为（）A.6B.12C.18D.2415、如图，能判定EB∥AC的条件是（）A.∠C＝∠ABEB.∠A＝∠EBDC.∠C＝∠ABCD.∠A＝∠ABE二、填空题(共10题，共计30分)16、如图，AB∥CD，∠1=64°，FG平分∠EFC，则∠EGF=________．17、两个角的两边分别平行，其中一个角是30°，则另一个角是________．18、如图，在中，，，点是的中点，连接，将沿射线方向平移，在此过程中，的边与的边、分别交于点、，当的面积是面积的时，则△BCD 平移的距离是________.19、将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起，若∠1＝25°，则∠2的度数为________．20、一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行.如图2：当∠CAE＝15°时，BC∥DE.则∠CAE（0°＜∠CAE＜180°）其它所有可能符合条件的度数为________.21、将一矩形纸条，按如图所示折叠，则∠1=________度.22、完成下面的证明．已知：如图，BC∥DE，BE、DF分别是∠ABC、∠ADE的平分线．求证：∠1＝∠2．证明：∵BC∥DE，∴∠ABC＝∠ADE（________）．∵BE、DF分别是∠ABC、∠ADE的平分线．∴∠3＝∠ABC，∠4＝∠ADE．∴∠3＝∠4．∴________∥________（________）．∴∠1＝∠2（________）．23、如图：已知，AB∥CD，∠1＝50°，那么∠2＝________°，∠3＝________°24、将一副三角板如图放置.若AE∥BC，则∠AFD=________.25、在△ABC中，∠B和∠C的平分线交于点F，过点F作DF∥BC ，交AB于点D，交AC于点E，若BD＋CE＝9，则线段DE的长为________.三、解答题(共5题，共计25分)26、如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，AB=6，FC=4，求线段DB的长．27、如图所示，AB∥CD∥EF，∠ABC＝55°，∠CEF＝150°，求∠BCE的度数．28、如图，矩形ABCD中，点E是CD延长线上一点，且，求证：．29、MF⊥NF于F，MF交AB于点E，NF交CD于点G，∠1=140°，∠2=50°，试判断AB和CD的位置关系，并说明理由．30、如图，一块边长为8米的正方形土地，在上面修了三条道路，宽都是1米，空白的部分种上各种花草．（1）请利用平移的知识求出种花草的面积．（2）若空白的部分种植花草共花费了4620元，则每平方米种植花草的费用是多少元？参考答案一、单选题(共15题，共计45分)1、B2、C3、B4、B5、C6、D7、C8、D9、C10、B11、B12、C13、B14、A15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、27、28、29、30、。

平行线常考经典较难题、压轴题例题例1 翻折（2018•仙居县一模）如图，把一张长方形纸带沿着直线GF折叠，∠CGF=30°，则∠1的度数是．【练习】（2018春•莒县期中）如图，生活中将一个宽度相等的纸条按图所示折叠一下，如果∠2=100°，那么∠1的度数为．例2 旋转（2017•上海中考）一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA与边FE叠合，顶点B、C、D在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180 ），如果EF∥AB，那么n的值是．【练习】1.（2017秋•前郭县期末改编）将一副直角三角尺ABC 和CDE 按如图方式放置，其中直角顶点C 重合，∠D=45°，∠A=30°．将三角形CDE 绕点C 旋转，若DE ∥BC ，则直线AB 与直线CE 的较大的夹角∠1的大小为 度．2.（2018春•滨海县期中）长江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图，灯A 射线自AM 顺时针旋转至AN 便立即回转，灯B 射线自BP 顺时针旋转至BQ 便立即回转，两灯不停交叉照射巡视．若灯A 转动的速度是a°/秒，灯B 转动的速度是b°/秒，且a 、b 满足|a ﹣3b |+（a +b ﹣4）2=0．假定这一带长江两岸河堤是平行的，即PQ ∥MN ，且∠BAN=45° （1）求a 、b 的值；（2）若灯B 射线先转动20秒，灯A 射线才开始转动，在灯B 射线到达BQ 之前，A 灯转动几秒，两灯的光束互相平行？（3）如图，两灯同时转动，在灯A 射线到达AN 之前．若射出的光束交于点C ，过C 作CD ⊥AC 交PQ 于点D ，则在转动过程中，∠BAC 与∠BCD 的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请求出其取值范围．1A EDBC例3 平行线的性质（2017春•南沙区期末）已知，直线AB∥DC，点P为平面上一点，连接AP与CP．（1）如图1，点P在直线AB、CD之间，当∠BAP=60°，∠DCP=20°时，求∠APC．（2）如图2，点P在直线AB、CD之间，∠BAP与∠DCP的角平分线相交于点K，写出∠AKC与∠APC之间的数量关系，并说明理由．（3）如图3，点P落在CD外，∠BAP与∠DCP的角平分线相交于点K，∠AKC与∠APC 有何数量关系？并说明理由．【练习】1. （2017春•武侯区校级期中）如图，已知AB∥CD，CE、BE的交点为E，现作如下操作：第一次操作，分别作∠ABE和∠DCE的平分线，交点为E1，第二次操作，分别作∠ABE1和∠DCE1的平分线，交点为E2，第三次操作，分别作∠ABE2和∠DCE2的平分线，交点为E3，…，第n次操作，分别作∠ABE n﹣1和∠DCE n﹣1的平分线，交点为E n．若∠E n=1度，那∠BEC等于度2．（2018春•宿豫区期中）如图，两直线AB、CD平行，则∠1+∠2+∠3+∠4+∠5=720°．3.（2018春•黄陂区期中）已知直线AB∥CD．（1）如图1，直接写出∠BME、∠E、∠END的数量关系为；（2）如图2，∠BME与∠CNE的角平分线所在的直线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论；（3）如图3，∠ABM=∠MBE，∠CDN=∠NDE，直线MB、ND交于点F，则=．4.（2017春•丰城市期末）数学思考：（1）如图1，已知AB∥CD，探究下面图形中∠APC和∠PAB、∠PCD的关系，并证明你的结论推广延伸：（2）①如图2，已知AA1∥BA1，请你猜想∠A1，∠B1，∠B2，∠A2、∠A3的关系，并证明你的猜想；②如图3，已知AA1∥BA n，直接写出∠A1，∠B1，∠B2，∠A2、…∠B n﹣1、∠A n的关系拓展应用：（3）①如图4所示，若AB∥EF，用含α，β，γ的式子表示x，应为( )A.180°+α+β﹣γB.180°﹣α﹣γ+βC．β+γ﹣αD．α+β+γ②如图5，AB∥CD，且∠AFE=40°，∠FGH=90°，∠HMN=30°，∠CNP=50°，请你根据上述结论直接写出∠GHM的度数是．例4 平移（2017春•上虞区期末）如图1所示，已知BC∥OA，∠B=∠A=120°（1）说明OB∥AC成立的理由．（2）如图2所示，若点E，F在BC上，且∠FOC=∠AOC，OE平分∠BOF，求∠EOC的度数．（3）在（2）的条件下，若左右平移AC，如图3所示，那么∠OCB：∠OFB的比值是否随之发生变化？若变化，请说明理由；若不变，请求出这个比值．（4）在（3）的条件下，当∠OEB=∠OCA时，求∠OCA的度数．【练习】如图，已知AM∥BN，∠A=60°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．（1）求∠CBD的度数；（2）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．（3）当点P运动到使∠ACB=∠ABD时，∠ABC的度数是．例5 作图—应用作图题（1）如图1，一个牧童从P点出发，赶着羊群去河边喝水，则应当怎样选择饮水路线，才能使羊群走的路程最短？请在图中画出最短路线．（2）如图2，在一条河的两岸有A，B两个村庄，现在要在河上建一座小桥，桥的方向与河岸方向垂直，桥在图中用一条线段CD表示．试问：桥CD建在何处，才能使A到B的路程最短呢？请在图中画出桥CD的位置．【练习】（2016春•湖州市吴兴区期末）如图，平面上有直线a及直线a外的三点A、B、P．（1）过点P画一条直线m，使得m∥a；（2）过B作BH⊥直线m，并延长BH至B′，使得BB′为直线a、m之间的距离；（3）若直线a、m表示一条河的两岸，现要在这条河上建一座桥（桥与河岸垂直），使得从村庄A经桥过河到村庄B的路程最短，试问桥应建在何处？画出示意图．【巩固练习】一、选择题图2图1PBA1．（2018春•洪山区期中）如图，AB∥DE，∠ABC的角平分线BP和∠CDE的角平分线DK 的反向延长线交于点P且∠P﹣2∠C=57°，则∠C等于（）A．24°B．34°C．26°D．22°第1题图第2题图2．（2018春•高新区校级期中）如图，AB∥CD，∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H，∠K﹣∠H=27°，则∠K=（）A．76°B．78°C．80°D．82°3．（2017春•祁阳县期末）在同一平面内，有8条互不重合的直线，l1，l2，l3…l8，若l1⊥l2，l2∥l3，l3⊥l4，l4∥l5…以此类推，则l1和l8的位置关系是（）A．平行B．垂直C．平行或垂直D．无法确定4．（2013春•汉阳区期末）如图，AB⊥BC，AE平分∠BAD交BC于点E，AE⊥DE，∠1+∠2=90°，M，N分别是BA，CD延长线上的点，∠EAM和∠EDN的平分线交于点F．下列结论：①AB∥CD；②∠AEB+∠ADC=180°；③DE平分∠ADC；④∠F为定值其中结论正确的有（）A．1个B．2个C．3个D．4个第4题图第5题图5．（2018•丰南区一模）如图所示，AB∥CD，则∠A+∠E+∠F+∠C等于（）A．180° B．360°C．540° D．720°二、填空题6．（2018春•雁塔区校级月考）平面上不重合的四条直线，可能产生交点的个数为个．7．（2018•河南模拟）如图所示，AB∥EF，∠B=35°，∠E=25°，则∠C+∠D的值为．第7题图第8题图第9题图8．（2018•昆山市二模）如图所示，AB∥CD，∠E=35°，∠C=20°，则∠EAB的度数为．9．（2017秋•遂宁期末）如图，AB∥EF∥CD，EG平分∠BEF，∠B+∠BED+∠D=192°，∠B﹣∠D=24°，则∠GEF=．10．（2017秋•福田区校级期末）已知D是△ABC的边BC所在直线上的一点，与B，C不重合，过D分别作DF∥AC交AB所在直接于F，DE∥AB交AC所在直线于E．若∠A=80°，则∠FDE的度数是．11．（2018春•开福区校级期末）学习了平行线后，小敏想出了过已知直线外一点画这条直线的平行线的新方法，她是通过折一张半透明的纸得到的，如图所示，由操作过程可知小敏画平行线的依据可以是．（把所有正确结论的序号都填在横线上）①如果两条直线和第三条直线平行，那么这两条直线平行；②同位角相等，两直线平行；③内错角相等，两直线平行；④同旁内角互补，两直线平行．12．（2018春•青山区期中）把一张对边互相平行的纸条折成如图那样，EF是折痕，若∠EFB=32°，则∠D′FD的度数为．13．（2018春•宁波期中）如图（1）所示为长方形纸带，将纸带沿EF折叠成图（2），再沿BF折叠成图（3），继续沿EF折叠成图（4），按此操作，最后一次折叠后恰好完全盖住∠EFG；整个过程共折叠了9次，问图（1）中∠DEF的度数是．三、解答题14. （余姚市校级期中）按要求解答下列问题：（1）分别按下列要求作出经过平移后的图形①把三角形ABC向右平移3格．②把第①题所得图形向上平移4格．（2）经（1）中二次平移后所得的图形，能通过三角形ABC一次平移得到吗？如果你认为可以，描述这个平移过程．（3）如图：直线l1，l2表示一条河的两岸，且l1∥l2，现要在河上建一座桥．桥建在何处才能使从村庄A经过河到村庄B的路程最短？画出示意图，并用平移的原理说明理由15．（2018春•甘井子区期中）如图1，MN∥PQ，直线AD与MN、PQ分别交于点A、D，点B在直线PQ上，过点B作BG⊥AD，垂足为点G．（1）求证：∠MAG+∠PBG=90°；（2）若点C在线段AD上（不与A、D、G重合），连接BC，∠MAG和∠PBC的平分线交于点H，请在图2中补全图形，猜想并证明∠CBG与∠AHB的数量关系；（3）若直线AD的位置如图3所示，（2）中的结论是否成立？若成立，请证明；若不成立，请直接写出∠CBG与∠AHB的数量关系．16．（2017春•嘉祥县期中）（1）如图甲，AB∥CD，∠2与∠1+∠3的关系是什么？并写出推理过程；（2）如图乙，AB∥CD，直接写出∠2+∠4与∠1+∠3+∠5的数量关系；（3）如图丙，AB∥CD，试问∠2+∠4+∠6与∠1+∠3+∠5+∠7还有类似的数量关系吗？若有，请直接写出，并将它们推广到一般情况，用一句话写出你的结论．17．（2017春•成都期中）已知AM∥CN，点B为平面内一点，AB⊥BC于B．（1）如图1，直接写出∠A和∠C之间的数量关系；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD=∠C；（3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数．18．（2017春•乐亭县期中）已知，∠AOB=90°，点C在射线OA上，CD∥OE．（1）如图1，若∠OCD=120°，求∠BOE的度数；（2）把“∠AOB=90°”改为“∠AOB=120°”，射线OE沿射线OB平移，得O′E，其他条件不变，（如图2所示），探究∠OCD、∠BO′E的数量关系；（3）在（2）的条件下，作PO′⊥OB垂足为O′，与∠OCD的平分线CP交于点P，若∠BO′E=α，请用含α的式子表示∠CPO′（请直接写出答案）．19．（2017春•碑林区校级期中）探究：如图①，已知直线l1∥l2，直线l3和l1，l2分别交于点C和D，直线l3上有一点P．（1）若点P在C、D之间运动时，问∠PAC，∠APB，∠PBD之间有怎样的关系？并说明理由．（2）若点P在C、D两点的外侧运动时（点P与点C、D不重合），请尝试自己画图，写出∠PAC，∠APB，∠PBD之间的关系，并说明理由．（3）如图②，AB∥EF，∠C=90°，我们可以用类似的方法求出∠α、∠β、∠γ之间的关系，请直接写出∠α、∠β、∠γ之间的关系．20．（2017春•汉阳区期中）如图1，AB∥CD，E是AB、CD之间的一点．（1）判定∠BAE，∠CDE与∠AED之间的数量关系，并证明你的结论；（2）如图2，若∠BAE、∠CDE的两条平分线交于点F．直接写出∠AFD与∠AED之间的数量关系；（3）将图2中的射线DC沿DE翻折交AF于点G得图3，若∠AGD的余角等于2∠E的补角，求∠BAE的大小．21．（2015春•越秀区校级期中）已知：如图，BC∥OA，∠B=∠A=100°，试回答下列问题：（1）如图①所示，求证：OB∥AC．（注意证明过程要写依据）（2）如图②，若点E、F在BC上，且满足∠FOC=∠AOC，并且OE平分∠BOF．（ⅰ）求∠EOC的度数；（ⅱ）求∠OCB：∠OFB的比值；（ⅲ）如图③，若∠OEB=∠OCA．此时∠OCA度数等于．（在横线上填上答案即可）22．（2015春•巴南区校级期末）如图，已知两条射线OM∥CN，动线段AB的两个端点A、B分别在射线OM、CN上，且∠C=∠OAB=108°，F在线段CB上，OB平分∠AOF，OE平分∠COF．（1）请在图中找出与∠AOC相等的角，并说明理由；（2）若平行移动AB，那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值；（3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=2∠OBA？若存在，请求出∠OBA度数；若不存在，说明理由．23．（2017春•江北区校级期中）已知直线AB∥CD．（1）如图1，直接写出∠ABE，∠CDE和∠BED之间的数量关系是．（2）如图2，BF，DF分别平分∠ABE，∠CDE，那么∠BFD和∠BED有怎样的数量关系？请说明理由．（3）如图3，点E在直线BD的右侧，BF，DF仍平分∠ABE，∠CDE，请直接写出∠BFD 和∠BED的数量关系．24．（2017春•锡山区校级月考）将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°；∠E=∠B=45°）：（1）若∠DCE=35°，求∠ACB的度数；（2）猜想∠ACB与∠DCE的数量关系，并说明理由；（3）请你动手操作，现将三角尺ACD固定，三角尺BCE的CE边与CA边重合，绕点C顺时针方向旋转，当0°＜∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE角度所有可能的值（不必说明理由）；若不存在，请说明理由．21世纪教育网–中小学教育资源及组卷应用平台。

题号一总分得分评卷人得分2．已知：如图，AF∥C D，∠AB C＝∠DEF，∠BCD＝∠EFA，求证：AB∥DE，（提示：连接A D）（2）本题隐含着一个规律，请你根据（1）的结果进行归纳，试着用文字表述出来．（3）利用（2）的结论解答：如果两个角的两边分别平行，其中一角是另一个角的2倍多6°，求这两个角的大小．（1）填空：∴（如果两条直线都和第三条直线平行，那么这两条直线也互相平行）∠EP D+＝180°（2）依照上面的解题方法，观察图（2），已知AB∥C D，猜想图中的∠BP D与∠B、∠D的数量关（3）观察图（3）和（4），已知AB∥C D，直接写出图中的∠BPD与∠B、∠D的数量关系，不用已知：如图，C D分别交A D、AE、BE于点D、F、C，连接AB、AC，A D∥BE，∠1＝∠2，∠3＝∠求证：AB∥C D．证明：∵A D∥BE（已知）∴∠3＝∠CA D（）∵∠3＝∠4（已知）∴∠4＝（等量代换）∵∠1＝∠2（已知）∴∠4＝（等量代换）∴AB∥C D．7．如图，∠1+∠2＝180°，∠3＝∠B，求证：EF∥BC，请你补充完成下面的推导过程．证明：∵∠1+∠2＝180°（已知）））））（））8．将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起，友情提示：∠A＝60°，∠D＝30°，∠E＝∠B＝45°．．．（2）由（1）猜想∠ACB与∠D C E的数量关系，并说明理由．（3）当∠ACE＜90°且点E在直线AC的上方时，当这两块三角尺有一组边互相平行时，请直接写出∠ACE角度所有可能的值（不必说明理由）．9．已知：如图，AB∥C D，∠B＝70°，∠BCE＝20°，∠CEF＝130°，请判断AB与EF的位置关系，并说明理由．解：，理由如下：∵AB∥C D，）∴∠BC D＝70°，（）∵∠BCE＝20°，∴∠EC D＝50°，∵∠CEF＝130°，∴+）11．观察发现：已知AB∥C D，点P是平面上一个动点．当点P在直线AB、C D的异侧，且在B C（不与点B、C重合）上时，如图（1），容易发现：∠ABP+∠D C P＝∠BP C．拓展探究：（1）当点P位于直线AB、C D的异侧，且在BC左侧时，如图（2），∠ABP、∠D C P、∠BPC之间有何关系？并说明理由．（2）当点P位于直线AB、C D的异侧，且在BC右侧时，如图（3），直接写出∠ABP、∠D C P、∠BP C之间关系．（3）当点P位于直线AB、C D的同侧，如图（4），直接写出∠ABP、∠D C P、∠BP C之间关系．°；请根据解答过程填空（理由或数学式）°；解：（1）则∠DA C＝（2）A D∥B C．理由：∵A D平分∠EAC（已知）∴∠DA C＝∠EA C＝∵∠C＝55°（已知）°（等式性质）∴∠C＝∠（）∴A D∥B C（）14．综合与探究如图，已知A M∥B N，∠A＝60°，点P是射线AM上一动点（与点A不重合）．BC、B D分别平分；，∴∠ABP＝2∠CBP、∠PB N＝∴2∠CBP+2∠DBP＝120°，∴∠CB D＝∠CBP+∠DBP＝【操作】，（）．（3）当点P运动时，∠APB与∠AD B之间的数量关系是否随之发生变化？若不变化，请写出它们之（4）当点P运动到使∠ACB＝∠AB D时，∠AB C的度数是．15．（1）如图 1，已知 AB ∥C D ，求证：∠BE D ＝∠1+∠2．16．填空，如图，已知∠1＝∠2，∠C ＝∠D ，求证：∠A ＝∠F ．证明：∵∠1＝∠2（已知）又∠1＝∠D M N （ ∴∠2＝∠D M N （等量代换）∴DB ∥E C （ ）））（m 为常数，且 0＜m ＜100）．（1）求∠A 、∠C 的度数（用含 m 的代数式表示）；（2）求证：AB ∥C D ；（3）若∠A ＝40°，∠BA M ＝20°，∠EF M ＝10°，直线 A M 与直线 F M 交于点 M ，直接写出∠AM F的度数．（2）如图2，∠BEF与∠EF D的角平分线交于点P，EP与C D交于点G，点H是M N上的一点且G H⊥E G．求证：PF∥G H．19．已知AB∥CD，点E为平面内一点，BE⊥CE于E．（2）如图2，过点E作EF⊥C D，垂足为F，求证：∠CEF＝∠ABE；（3）如图3，在（2）的条件下，作E G平分∠CEF，交DF于点G，作E D平分∠BEF，交C D于D，连接B D，若∠D BE+∠AB D＝180°，且∠B DE＝3∠GEF，求∠BEG的度数．20．如图，已知A D∥B C，∠A＝∠C＝50°，线段A D上从左到右依次有两点E、F（不与A、D重合）（1）AB与C D是什么位置关系，并说明理由；（2）观察比较∠1、∠2、∠3的大小，并说明你的结论的正确性；（3）若∠FB D：∠CB D＝1：4，BE平分∠ABF，且∠1＝∠B D C，求∠FB D的度数，判断BE与A D是何种位置关系？21．已知A M∥C N，点B为平面内一点，AB⊥BC于B（1）如图1，直接写出∠A和∠C之间的数量关系；（2）如图2，过点B作B D⊥A M于点D，求证：∠AB D＝∠C；（3）如图3，在（2）问的条件下，点E、F在D M上，连接BE、BF、CF，BF平分∠DB C，BE平分∠AB D，若∠FC B+∠N CF＝180°，∠ABF＝2∠ABE，求∠EB C的度数．22．如图，已知A M∥B N，∠A＝52°，点P射线A M上，动点（与点A不重合），BC、B D分别平分∠ABP和∠PBN，分别交射线AM于点C，D．（2）当点P运动时，∠APB与∠AD B之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由，若变化，请写出变化规律；（3）当点P运动到使∠ACB＝∠AB D时，求∠AB C的度数．．．如图2，AB∥C D，线段M N把ABC D这个封闭区域分为I、Ⅱ两部分（不含边界），点E是位于这两个区域内的任意一点，请直接写出∠E M B、∠EN D、∠M E N的关系．24．（1）如图①，若AB∥C D，求∠B+∠D+∠E的度数？1（2）如图②，若AB∥C D，求∠B+∠D+∠E+∠E的度数？1212312n（3）画图并猜想：在（2）的条件下，请在备用图中，过点G作∠AFB两边的垂线，垂足分别为M、N猜想线段G M、G N的大小．阅读下列解题过程：所以∠BE D＝∠1+∠2＝38°+35°＝73°（等量代换）然后解答下列问题：如图2和图3，是明明设计的智力拼图玩具的一部分，现在明明遇到两个问题，请你帮他解决：；27．在一次数学活动课上，老师让同学们用两个大小、形状都相同的三角板画平行线AB、C D，并说出自己做法的依据．小琛、小萱、小冉三位同学的做法如下：小琛说：“我的做法的依据是内错角相等，两直线平行”（回答正确或错误）小琛说的是否正确？小萱做法的依据是小冉做法的依据是28．已知如图，直线EF与AB、C D分别相交于点E、F．（1）如图1，若∠1＝120°，∠2＝60°，求证AB∥C D；（2）在（1）的情况下，若点P是平面内的一个动点，连结PE、PF，探索∠EPF、∠PEB、∠PFD 三个角之间的关系；①当点P在图2的位置时，可得∠EPF＝∠PEB+∠PF D；请阅读下面的解答过程，并填空（理由或数学式）．．＝∠PEB+∠PF D（等式的性质）即∠EPF＝∠PEB+∠PF D．（2）如图②，∠M A E＝140°，∠FE G＝30°，当∠NCE＝30．有两个∠A O B与∠E D C，∠ED C保持不动，且∠E D C的一边CD∥A O，另一边D E与直线OB 相交于点F．；（2）在（1）②的前提下，若∠AO B＝α，∠E D C＝β，且α＜β，请直接写出∠BFE的度数（用含α、β的式子表示）．31．如图，某工程队从A点出发，沿北偏西67°方向修一条公路A D，在B D路段出现塌陷区，就改以下是小刚不完整的解答，请帮他补充完整．解：由已知平行，得∠1＝∠A＝67°（两直线平行，）∴∠CB D＝23°+67°＝当∠ECB+∠CB D＝）°此时CE⊥BC．（）32．如图，已知直线AB∥C D，∠A＝∠C＝100°，E，F在C D上，且满足∠DBF＝∠AB D，BE平分∠CBF．（3）若平行移动A D，在平行移动A D的过程中，是否存在某种情况，使∠BEC＝∠AD B？若存在，求出∠A D B；若不存在，请说明理由．33．如图，已知AB∥C D，C在D的右侧，BE平分∠ABC，D E平分∠A D C，BE、DE所在直线交于点E．∠A D C＝70°．（1）求∠E D C的度数；（2）若∠AB C＝n°，求∠BE D的度数（用含n的式子表示）；（3）将线段BC沿D C方向平移，使得点B在点A的右侧，其他条件不变，画出图形并判断∠BED 的度数是否改变，若改变，求出它的度数（用含n的式子表示），不改变，请说明理由．34．如图，已知直线l∥l，点A、B分别在l与l上．直线l和直线l、l交于点C和D，在直线1212312（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PB D有怎样的数量关系？请说明理由．（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD 之间的关系又是如何？35．如图1，已知两条直线AB，C D被直线EF所截，分别交于点E，点F，E M平分∠AEF交C D于点M，且∠FE M＝∠F M E．（2）如图2，点G是射线M D上一动点（不与点M，F重合），E H平分∠FE G交CD于点H，过点H作H N⊥E M于点N，设∠E H N＝α，∠E GF＝β．①当点G在点F的右侧时，若β＝50°，求α的度数；②当点G在运动过程中，α和β之间有怎样的数量关系？请写出你的猜想，并加以证明．（2）如图2，若∠AB M＝∠ABF，∠C D M＝∠C D F，写出∠M与∠BE D之间的数量关系，并说明理由；（3）若∠AB M＝∠ABF，∠C D M＝∠C D F，设∠BE D＝m°，直接写出用含m°，n的代数式表示∠M＝．°（）°所以∠FE D+∠CD E＝所以EF∥39．如图所示，把一根筷子一端放在水里，一端露出水面，筷子变弯了，它真的弯了吗？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变．（1）请指出与∠1是同旁内角的有哪些角？请指出与∠2是内错角的有哪些角？（2）若∠1＝115°，测得∠B O M＝145°，从水面上看斜插入水中的筷子，水下部分向上折弯了多少度？请说明理由．40．实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．（1）如图，一束光线m射到平面镜上，被a镜反射到平面镜b上，又被b镜反射，若被b镜反射出参考答案与试题解析一．解答题（共40小题）1．解：∵∠1＝∠2，∴a∥b，∵∠3＝115°，∴∠5＝180°﹣∠3＝65°，∴∠4＝65°．2．证明：如图，连接A D，∵AF∥C D，∴∠DAF＝∠C D A，又∵∠ABC＝∠D EF，∠BC D＝∠EFA，四边形ABC D与四边形A D EF的内角和都等于360°，∴∠BA D＝∠E D A，∴AB∥DE．∴∠4+∠2＝180°，∴∠4＝180°﹣∠2＝65°；（2）由（1）可知：如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补，故答案为：如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补；（3）由（2）可知这两个角互补，设一个角为x°，则另一个角为2x°+6°，根据两个角互补可得，x+2x+6＝180，解得x＝58，∵AB∥C D，EF∥AB，∴∠EP D+∠D＝180°，∴∠BP D＝∠B+∠D；∵EP∥AB，∴C D∥EP（如果两条直线都和第三条直线平行，那么这两条直线也互相平行），∴∠D＝∠BP D+∠B；理由是：∵EP∥AB，∴∠B＝∠BP D+∠D．∴∠4＝∠CA D（等量代换）∵∠1＝∠2（已知）∴∠3＝∠F D H（等量代换）∴EF∥BC（内错角相等，两直线平行）故答案为：对顶角相等，1，同旁内角互补，两直线平行；两直线平行，同位角相等；已知，F D H，等量代换，内错角相等，两直线平行．8．解：（1）①∵∠D CE＝45°，∠AC D＝90°∵∠BCE＝90°②∵∠ACB＝140°，∠ECB＝90°（2）猜想：∠ACB+∠D C E＝180°理由如下：∵∠AC E＝90°﹣∠D C E 又∵∠ACB＝∠AC E+90°∴∠EC D＝50°，∵CEF＝130°，∴∠E+∠D C E＝180°，∴EF∥C D，（同旁内角互补，两直线平行）∴AB∥EF．（平行于同一直线的两条直线互相平行）故答案为：AB∥EF，两直线平行，内错角相等；等量代换，∠E，∠D C E，C D，同旁内角互补，两直线平行；平行于同一直线的两条直线互相平行．10．∴∠C O A＝∠ABC＝80°，∴∠AB O＝∠B O C＝6x＝48°．∴x＝10°，理由：如图，过点P作直线P Q∥AB，故答案为：50；50；（2）∵A D平分∠EAC（已知）∴∠C＝∠DA C（等量代换）∴A D∥B C（内错角相等，两直线平行）故答案为：55，DA C，等量代换；内错角相等，两直线平行14．解：（1）∵A M∥B N，∴∠AC B＝∠CB N；故答案为：CB N；（2）：∵A M∥BN，∴∠ABN+∠A＝180°，∵∠A＝60°，∴∠ABN＝120°，∴∠ABP+∠PB N＝120°，∵BC平分∠ABP，B D平分∠PB N，∴∠ABP＝2∠CBP、∠PB N＝2∠PB D，（角平分线的定义）∴2∠CBP+2∠DBP＝120°，∴∠CB D＝∠CBP+∠DBP＝60°，故答案为：120°；2∠PB D；角平分线的定义；60°；（3）不变，∠APB：∠A D B＝2：1．∵A M∥B N，∴∠APB：∠A DB＝2：1；（4）∵A M∥B N，∴∠ABC＝30°，故答案为：30°．∴AB∥C D∥EF，∴∠3＝∠1，∠4＝∠2，∴∠3+∠4＝∠1+∠2，即∠BE D＝∠1+∠2；∴AB∥EF∥G H∥C D，∴∠1＝∠3，∠4＝∠5，∠6＝∠2，∴∠1+∠5+∠6＝∠3+∠4+∠2，即∠1+∠E G H＝∠2+∠BE G；（3）由题可得，向左的角度数之和与向右的角度数之和相等，∴∠1、∠3、∠5与∠2、∠4、∠6之间的关系为：∠1+∠3+∠5＝∠2+∠4+∠6．∴∠2＝∠D M N（等量代换）故答案为：对顶角相等；同位角相等，两直线平行；两直线平行，同旁内角互补；∠D；同旁内角互补，两直线平行；两直线平行，内错角相等．（3）当∠A＝m+20°＝40°时，∠C＝m+80°＝100°，理由：如图1，∵∠1与∠2互补，∴∠1+∠2＝180°．∵G H⊥E G，∴PF∥G H．（2）如图2中，作E M∥C D，∵E M∥C D，C D∥AB，∴AB∥C D∥E M，∴∠F＝90°，∴∠FE M＝90°，∵E G平分∠CEF，∴∠CEF＝2∠FEG＝2α，∴∠ABE＝∠CEF＝2α，∵AB∥C D∥E M，∵∠BEC＝90°，∵∠DBE+∠AB D＝180°，∠AB D+∠B D F＝180°，∴∠DBE＝∠B D F＝∠B DE+∠E D F＝3α+β，∵∠ABK＝180°，∴∠C+∠AB C＝180°，∴AB∥C D；（2）∠1＞∠2＞∠3，∵A D∥B C，（3）∵A D∥B C，∴∠1＝∠EBC，∵AB∥C D，∴∠B D C＝∠ABD，∵∠1＝∠B D C，∵AB⊥BC，∴∠A+∠A O B＝90°，∴∠A+∠C＝90°；设∠DBE＝α，∠ABF＝β，则β+β+2α＝90°，②∴∠EBC＝∠ABE+∠AB C＝15°+90°＝105°．∴∠APB＝∠PB N，∠A DB＝∠DB N，又∵B D平分∠PB N，∴∠PBN＝2∠DBN，∴∠APB＝2∠A D B；（3）∵A D∥B N，∴∠ACB＝∠CBN，又∵∠ACB＝∠AB D，∴∠CB N＝∠ABD，∴∠ABC＝∠DBN，由（1）可得，∠C B D＝64°，∠AB N＝128°，∴∠ABC＝（128°﹣64°）＝32°．∵AB∥C D，∴AB∥C D∥EF，②同理可得，∴∠AEC＝∠1+∠2＝65°；③猜想：∠AEC＝∠EAB+∠EC D．∴EF∥AB（平行于同一条直线的两直线平行），∴∠1＝∠EAB，∠2＝∠EC D（两直线平行，内错角相等），∴∠AEC＝∠1+∠2＝∠EAB+∠EC D（等量代换）．（2）当点E位于区域Ⅰ时，∠E M B+∠EN D+∠M E N＝360°，∴AB∥C D∥EF，∴∠B M E+∠M E F＝180°，∠D NE+∠NEF＝180°，∴∠E M B+∠EN D+∠M E N＝360°；当点E位于区域Ⅱ时，∠E M B+∠E N D＝∠M E N，理由：过E作EF∥AB，∵AB∥C D，∴AB∥C D∥EF，24．解：（1）如图①，过E作E F∥AB，则E F∥C D，111∴∠B+∠1＝180°①，∠D+∠1＝180°②，①+②得∠B+∠1+∠D+∠2＝360°，即∠B+∠D+∠E＝360°；1121212∴∠B+∠D+∠E+∠E＝∠1+∠B+∠2+∠3+∠4+∠D＝540°＝3×180°；1212∴∠B+∠BE E＝180°，∠E E F+∠E E F＝180°，∠E E F+∠E E F＝180°，∠DE F+∠D ＝180°，∴∠B+∠D+∠E+∠E+∠E＝720°；12312n∵∠1+∠2＝180°，∴∠3+∠2＝180°，∴BF∥DE；∴∠AF G＝90°﹣45°＝45°；26．解：（1）由例题的结论可知，若AB∥DE，则∠A＝∠AC D﹣∠D＝66°﹣29°＝37°；故答案为：37°；故答案为：正确；同位角相等两直线平行或同旁内角互补两直线平行；内错角相等两直线平行或同旁又∵∠2＝60°，∴∠B OE＝∠1＝115°，∵∠B O M＝145°，∴∠M O E＝∠B O M﹣∠B O E＝145°﹣115°＝30°，∴向上折弯了30°．40．解：（1）∵入射角与反射角相等，即∠1＝∠4，∠5＝∠6，根据邻补角的定义可得∠7＝180°﹣∠1﹣∠4＝80°，根据m∥n，所以∠2＝180°﹣∠7＝100°，所以∠5＝∠6＝（180°﹣100°）÷2＝40°，根据三角形内角和为180°，所以∠3＝180°﹣∠4﹣∠5＝90°；故答案为：100，90．（3）理由：因为∠3＝90°，又由题意知∠1＝∠4，∠5＝∠6，所以∠2+∠7＝180°﹣（∠5+∠6）+180°﹣（∠1+∠4），＝360°﹣2∠4﹣2∠5，＝360°﹣2（∠4+∠5），∴∠B OE＝∠1＝115°，∵∠B O M＝145°，∴∠M O E＝∠B O M﹣∠B O E＝145°﹣115°＝30°，∴向上折弯了30°．40．解：（1）∵入射角与反射角相等，即∠1＝∠4，∠5＝∠6，根据邻补角的定义可得∠7＝180°﹣∠1﹣∠4＝80°，根据m∥n，所以∠2＝180°﹣∠7＝100°，所以∠5＝∠6＝（180°﹣100°）÷2＝40°，根据三角形内角和为180°，所以∠3＝180°﹣∠4﹣∠5＝90°；故答案为：100，90．（3）理由：因为∠3＝90°，又由题意知∠1＝∠4，∠5＝∠6，所以∠2+∠7＝180°﹣（∠5+∠6）+180°﹣（∠1+∠4），＝360°﹣2∠4﹣2∠5，＝360°﹣2（∠4+∠5），。