二次函数在几何方面的的应用

几何画板二次函数案例二次函数在几何画板中的应用非常广泛，下面我将为你提供一个案例，详细解释如何使用二次函数来构建一个几何图形。

案例：构建一个抛物线喷泉喷泉是一种常见的城市景观和装置，它通过一个喷水装置将水以特定的形式喷射出来，形成美丽的水柱。

在这个案例中，我们将使用二次函数来模拟喷泉的形状。

首先，让我们定义一个二次函数来描述喷泉的形状。

假设水柱的高度(h)是和喷射距离(x)相关的，我们可以使用以下二次函数来描述这种关系：h(x) = ax^2 + bx + c其中，a、b、c是需要确定的常数。

喷泉的形状通常是一个开口朝下的抛物线，所以a的值应该小于0。

接下来，我们将确定a、b和c的值。

为了简化问题，我们假设喷泉的最高高度是10米，并且喷射的最远距离是20米。

我们可以选择两个点来确定这个二次函数的值。

假设我们选择喷泉的两个关键点分别是(0,0)和(20,10)。

将这两个点带入二次函数的方程，我们可以得到以下两个方程：0=a*0^2+b*0+c=>c=010=a*20^2+b*20+0=>400a+20b=10通过解这个方程组，我们可以得到a和b的值。

解方程组可以得到a=-0.0125和b=0.25、所以二次函数的方程为：h(x)=-0.0125x^2+0.25x现在，我们可以使用这个二次函数来绘制喷泉的形状。

通过在几何画板上画出一系列点，然后使用平滑曲线连接这些点，我们可以得到整个喷泉的形状。

首先，我们选择几个x的值，例如x=0,2,4,...,20。

然后，我们使用二次函数计算对应的h(x)的值。

最后，在几何画板上画出这些点，并使用平滑曲线连接它们。

通过加入适当的颜色和细节，我们可以使这个几何图形更加真实和立体感。

我们还可以添加其他元素，如水柱顶部的喷雾效果。

通过调整二次函数的参数，我们可以自由地改变喷泉的形状和高度。

这使得几何画板成为优秀的工具，用于设计和模拟各种喷泉的形状，并选择出最佳的设计。

二次函数的应用题型一 几何型【例1】如图，等腰直角三角形ABC 的直角边与正方形DEFG 的边长均为2，AC 与DE 在同一直线上，开始时C 与D 重合，ABC 沿这条直线向右平移，直到A 与E 重合为止．设CD 的长为x ，ABC 与正方形DEFG 重合部分的面积为y ，则y 与x 之间的函数关系的图象大致是（ ）A B C D【例2】如图，在ABC 中，90,12,24B AB mm BC mm ∠===，动点P 从点A 开始沿边AB 向B 以2/mm s 的速度移动（不与点B 重合），点Q 从点B 开始沿边BC 向C 以4/mm s 的速度移动（不与点C 重合）．如果,P Q 分别从,A B 同时出发，那么经过 秒，四边形APQC 的面积最小．【例3】如图，在矩形ABCD 中，()0,8AB m m BC =>=，E 为线段BC 上的动点（不与,B C 重合）．连结DE ，作EF DE ⊥，EF 与射线BA 交于点F ，设,CE x BF y ==． （1）求y 关于x 的函数关系式；（2）若8m =，求x 为何值时，y 的值最大，最大值是多少？ （3）若12y m=，要使DEF 为等腰三角形，m 的值应为多少？【例4】小张要围一个矩形花圃，花圃的一边利用足够长的墙，另三边用总长为32米的篱笆恰好围成．围成的花圃是如图所示的矩形ABCD ．设AB 边的长为x 米，矩形ABCD 的面积为S 平方米． （1）求S 与x 之间的函数关系式；（2）当x 为何值时，S 有最大值？并求出最大值．题型二 图象型【例5】从地面竖立向上抛出一个小球，小球的高度h 与小球运动时间t 之间的关系式为2305h t t =-，那么小球从抛出至回落到地面所需要的时间是 ．【例6】某种火箭竖直向上发射时，它的高度()h m 与时间()t s 的关系可以用公式2515010h t t =-++表示，则经过______s ，火箭达到它的最高点．【例7】如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千．拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为 米．【例8】如图，人工喷泉有一个竖直的喷水枪AB ，喷水口A 距地面2米，喷水水流的轨迹是抛物线，如果要求水流的最高点P 到喷水枪AB 所在直线的距离为1米，且水流着地点C 距离水枪底部B 的距离为2.5米，那么水流的最高点距离地面是多少米？APDCB【例9】如图，足球场上守门员在O 处开出一高球，球从离地面1米的A 处飞出（A 在y 轴上），运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ，距地面约4米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．（1）求足球开始飞出到第一次落地时，该抛物线的表达式． （2）足球第一次落地点C 距守门员多少米？（3）运动员乙要抢到第二个落点D ，他应再向前跑多少米？【例10】如图，小明在一次高尔夫球争霸赛中，从山坡下O 点打出一球向球洞A 点飞去，球的飞行路线为抛物线，如果不考虑空气阻力，当球达到最大水平高度12米时，球移动的水平距离为9米．已知山坡OA 与水平方向OC 的夹角为30，83OA 米． （1）求出点A 的坐标及直线OA 的解析式； （2）求出球的飞行路线所在抛物线的解析式；（3）判断小明这一杆能否把高尔夫球从O 点直接打入球洞A 点 ．MA DC B Oyx421题型三 实际型【例11】儿童商场购进一批M 型服装，销售时标价为75元/件，按8折销售仍可获利50%．商场现决定对M 型服装开展促销活动，每件在8折的基础上再降价x 元销售，已知每天销售数量y （件）与降价x （元）之间的函数关系式为()2040y x x =+>． （1）求M 型服装的进价；（2）求促销期间每天销售M 型服装所获得的利润的最大值．【例12】随着南宁近几年城市建设的快速发展，对花木的需求量逐年提高．某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润1y 与投资量x 成正比例关系，如图①所示；种植花卉的利润2y 与投资量x 成二次函数关系，如图②所示（利润与投资量的单位：万元）．（1）分别求出利润1y 与2y 关于投资量x 的函数关系式；（2）若这位园林专业户投资8万元种植花卉和树木，他至少获得多少利润？至多获得多少利润？。

二次函数的几何应用教案道客巴巴
二次函数是数学中非常重要的一个概念，它在几何中有着广泛
的应用。

下面我将从几何图形的性质、实际问题的建模等方面来详
细解释二次函数的几何应用。

首先，二次函数在几何中常常与抛物线相关联。

抛物线是二次
函数的图像，它的几何特征包括顶点、焦点、直径、对称轴等。

通
过学习二次函数，我们可以深入理解抛物线的性质，比如开口方向、开口大小、顶点坐标等。

这些性质在解决与抛物线相关的几何问题
时非常有用，比如确定抛物线的焦点和直径、求解抛物线与直线的
交点等。

其次，二次函数还可以用来建立实际问题的数学模型。

例如，
抛物线的形状可以用来描述抛射物的运动轨迹，这在物理学和工程
学中有着广泛的应用。

通过二次函数建立的模型，我们可以计算抛
射物的最大高度、飞行时间、落地点等信息，这对于设计弹道导弹、射击运动员的训练等具有重要意义。

此外，二次函数还可以用来解决与面积和体积相关的几何问题。

比如，通过二次函数的图像，我们可以求解封闭图形的面积，或者
利用二次函数建立立体图形的体积模型。

这些都是二次函数在几何中的重要应用之一。

总之，二次函数在几何中有着广泛的应用，它不仅可以帮助我们理解抛物线的性质，还可以用来解决实际问题并建立数学模型。

通过深入学习二次函数的几何应用，我们可以更好地理解数学与现实世界的联系，提高数学建模和解决实际问题的能力。

希望这些内容能够对你有所帮助。

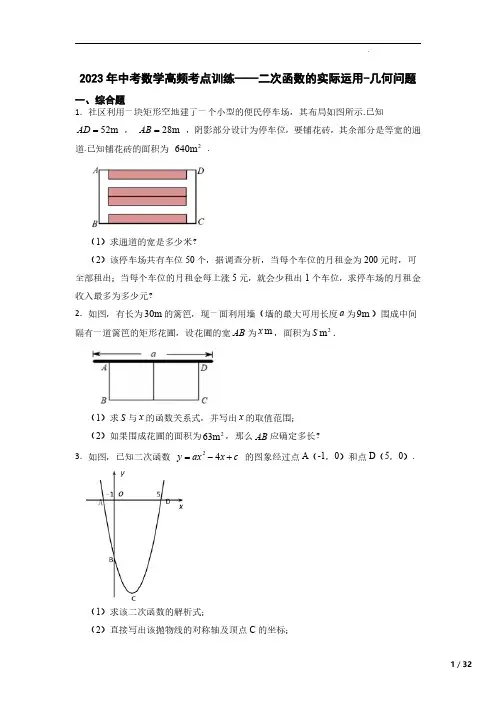
2023年中考数学高频考点训练——二次函数的实际运用-几何问题一、综合题1．社区利用一块矩形空地建了一个小型的便民停车场，其布局如图所示.已知52m AD =，28m AB =，阴影部分设计为停车位，要铺花砖，其余部分是等宽的通道.已知铺花砖的面积为2640m .（1）求通道的宽是多少米？（2）该停车场共有车位50个，据调查分析，当每个车位的月租金为200元时，可全部租出；当每个车位的月租金每上涨5元，就会少租出1个车位，求停车场的月租金收入最多为多少元？2．如图，有长为30m 的篱笆，现一面利用墙（墙的最大可用长度a 为9m ）围成中间隔有一道篱笆的矩形花圃，设花圃的宽AB 为m x ，面积为2m S ．（1）求S 与x 的函数关系式，并写出x 的取值范围；（2）如果围成花圃的面积为263m ，那么AB 应确定多长？3．如图，已知二次函数24y ax x c =-+的图象经过点A （-1，0）和点D （5，0）.（1）求该二次函数的解析式；（2）直接写出该抛物线的对称轴及顶点C 的坐标；（3）点B是该抛物线与y轴的交点，求四边形ABCD的面积.4．如图，抛物线顶点A的坐标为（1，4），抛物线与x轴相交于B、C两点，与y轴交于点E（0，3）.（1）求抛物线的表达式；（2）已知点F（0，﹣3），在抛物线的对称轴上是否存在一点G，使得EG+FG最小，如果存在，求出点G的坐标；如果不存在，请说明理由.5．如图，用一段长为32米的篱笆围成一个一边靠墙的矩形苗圃园，墙长为18米，设这个苗圃园垂直于墙的一边AB的长为x米，苗圃园的面积为y平方米.（1）求y关于x的函数表达式.（2）当x为何值时，苗圃的面积最大？最大值为多少平方米？6．如图，将直角三角形截出一个矩形PMCN，∠C＝90°，AC＝6，BC＝3，点P，M，N分别在AB，AC，BC上，设CN＝x．（1）试用含x的代数式表示PN，并写出x的范围;（2）设矩形PMCN的面积为y，当x为何值时，y取得的最大值是多少?7．如图，依靠一面长18米的墙，用34米长的篱笆围成一个矩形场地花圃ABCD，AB 边上留有2米宽的小门EF（用其他材料做，不用篱笆围）．（1）若矩形场地面积为160平方米，求矩形场地的长和宽．（2）矩形场地的长和宽为多少时，矩形场地的面积最大，并求出最大面积．8．某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙（墙足够长），已知计划中y m．的建筑材料可建围墙的总长度为50m．设饲养室为长为x（m），占地面积为()2（1）如图1，问饲养室为长x为多少时，占地面积y最大？（2）如图2，现要求在图中所示位置留2m的门，且仍使饲养室占地面积最大．小敏说：“只要饲养室长比（12m就行了．”请你通过计算，判断小敏的说法是否符合题意．9．如图，点O为矩形ABCD内部一点，过点O作EF AD交AB于点E，交CD于点F，过点O作GH AB交AD于点G，交BC于点H，设CH＝x，BH＝8－2x，CF＝x+2，DF＝3x－3．（1）x的取值范围是；（2）矩形BCFE的周长等于；（3）若矩形ABCD的面积为42，x的值为；（4）求矩形OFCH的面积S的取值范围．10．如图，某小区有一块靠墙（墙的长度30m）的空地，为美化环境，用总长为60m 的篱笆围成矩形花圃（矩形一边靠墙一侧不用篱笆，篱笆的厚度不计）．（1）如图1，怎么才能围成一个面积为2432m的矩形花圃；（2）如图2，若围成四块矩形且面积相等的花圃，设BC的长度为m x，求x的取值范围及矩形区域ABCD的面积的最大值．11．如图，某小区有一块靠墙（墙的长度不限）的矩形ABCD，为美化环境，用总长为90m的篱笆围成四块矩形，其中S1＝S2＝S3＝12S4（靠墙一侧不用篱笆，其余部分均使用，篱笆的厚度不计）．（1）若AE＝x，用含有x的式子表示BE的长；（2）求矩形ABCD的面积y关于x的解析式，并直接写出当面积取得最大值时，AE的长．12．矩形管在我们日常生活中应用广泛，石油、天然气的运输，制造建筑结构网架，制造公路桥梁等领域均有应用．如图，若矩形管ABCD的两边长20,6AB cm AD cm==，（1）若点PQ分别从A B、同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q 在边BC 上沿BC 方向以每秒1cm 的速度匀速运动，当一点到达终点时，另一点也停止运动．设运动时间为x 秒，PBQ 的面积为()2y cm ．求PBQ 面积的最大值；（2）若点P 在边AB 上，从点A 出发，沿AB 方向以每秒2cm 的速度匀速运动，点Q 在边BC 上，从BC 中点出发，沿BC 方向以每秒1cm 的速度匀速运动，当点P 运动到AB 中点时，点Q 开始向上运动，当一点到达终点时，另一点也停止运动．设点P 运动时间为t 秒，PBQ 的面积为2mcm ．求m 与t 的函数关系式．13．某公司对办公大楼一块墙面进行如图所示的图案设计.这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形，设小正方形的边长m ，直角三角形较短直角边长n ，且n ＝m ﹣2，大正方形的面积为S.（1）求S 关于m 的函数关系式；（2）若小正方形边长不大于3，当大正方形面积最大时，求m 的值.14．如图（1）问题提出如图1，在ABCD 中，45A ∠=︒，8AB =，6AD =，E 是AD 的中点，点F 在DC 上且5DF =求四边形ABFE 的面积.（结果保留根号）（2）问题解决某市进行河滩治理，优化美化人居生态环境.如图2所示，现规划在河畔的一处滩地上建一个五边形河畔公园ABCDE 按设计要求，要在五边形河畔公园ABCDE 内挖一个四边形人工湖OPMN ，使点O 、P 、M 、N 分别在边BC 、CD 、AE 、AB 上，且满足22BO AN CP ==，AM OC =.已知五边形ABCDE 中，90A B C ∠=∠=∠=︒，800m AB =，1200m BC =，600m CD =，900m AE =.满足人工湖周边各功能场所及绿化用地需要，想让人工湖面积尽可能小.请问，是否存在符合设计要求的面积最小的四边形人工湖OPMN ？若存在，求四边形OPMN 面积的最小值及这时点N 到点A 的距离；若不存在，请说明理由.15．如图，因疫情防控需要，某校在足够大的空地利用旧墙MN 和隔离带围成一个矩形隔离区ABCD ，已知墙长a 米，AD≤MN ，矩形隔离区的一边靠墙，另三边一共用了200米长的隔离带．（1）a=30，所围成的矩形隔离区的面积为1800平方米，求所利用旧墙AD 的长；（2）若a=150．求矩形隔离区ABCD 面积的最大值．16．如图，抛物线28y ax bx =++(0)a ≠经过(2,0)A -，(4,0)C 两点，点B 为抛物线的顶点，抛物线的对称轴与x 轴交于点D.（1）求抛物线的解析式；（2）动点P 从点B 出发，沿线段BD 向终点D 作匀速运动，速度为每秒1个单位长度，运动时间为t ，过点P 作PM BD ⊥，交BC 于点M ，以PM 为正方形的一边，向上作正方形PMNQ ，边QN 交BC 于点R ，延长NM 交AC 于点E .①当t 为何值时，点N 落在抛物线上；②在点P 运动过程中，是否存在某一时刻，使得四边形ECRQ 为平行四边形？若存在，求出此时刻的t 值；若不存在，请说明理由.17．如图，在平面直角坐标系中，点O 为坐标原点，抛物线2y x bx c =++交x 轴于A ，B 两点，交y 轴于点C ，直线3y x =-经过B ，C 两点.（1）求抛物线的解析式；（2）过点C 作直线CD y ⊥轴交抛物线于另一点D ，点P 是直线CD 下方抛物线上的一个动点，且在抛物线对称轴的右侧，过点P 作PE x ⊥轴于点E ，PE 交CD 于点F ，交BC 于点M ，连接AC ，过点M 作MN AC ⊥于点N ，设点P 的横坐标为t ，线段MN 的长为d ，求d 与t 之间的函数解析式（不要求写出自变量t 的取值范围）；（3）在（2）的条件下，连接PC ，过点B 作BQ PC ⊥于点Q （点Q 在线段PC 上），BQ 交CD 于点T ，连接OQ 交CD 于点S ，当ST TD =时，求线段MN 的长.18．如图，抛物线2y x bx c =++经过A （－3，0），B （1，0）两点，与y 轴交于点C ，P 为y 轴上的动点，连接AP ，以AP 为对角线作正方形AMPN.（1）求抛物线的解析式；（2）当正方形AMPN 与△AOP 面积之比为5∶2时，求点P 的坐标；（3）当正方形AMPN 有两个顶点在抛物线上时，直接写出点P 的坐标.19．如图，抛物线214y x bx c =-++经过点()6,0C ，顶点为B ，对称轴2x =与x 轴相交于点A ，D 为线段BC 的中点.（1）求抛物线的解析式；（2）P 为线段BC 上任意一点，M 为x 轴上一动点，连接MP ，以点M 为中心，将MPC 逆时针旋转90︒，记点P P 的对应点为E ，点C 的对应点为F.当直线EF 与抛物线214y x bx c =-++只有一个交点时，求点M 的坐标.20．如图，已知抛物线y=ax 2+bx+c(a≠0)的顶点坐标为Q(2，-1)，且与y 轴交于点C(0，3)，与x 轴交于A ，B 两点(点A 在点B 的右侧)，点P 是该抛物线上的一动点，从点C 沿抛物线向点A 运动(点P 与A 不重合)，过点P 作PD ∥y 轴，交AC 于点D.（1）求该抛物线的函数关系式；（2）当△ADP 是直角三角形时，求点P 的坐标；（3）在题(2)的结论下，若点E 在x 轴上，点F 在抛物线上，问是否存在以A 、P 、E 、F 为顶点的平行四边形？若存在，求点F 的坐标；若不存在，请说明理由.答案解析部分1．【答案】（1）解：设通道的宽为x 米，根据题意得：()()522282640x x --=，解得：34x =（舍去）或6x =，答：通道的宽为6米；（2）解：设月租金上涨a 元，停车场的月租金收入为y 元，根据题意得：()200505a y a ⎛⎫=+- ⎪⎝⎭，整理，得()2125101255y a =--+，所以，当25a =时，y 有最大值为10125；答：每停车场的月租金收入最多为10125元.【解析】【分析】（1）设通道的宽为x 米，根据矩形的面积公式列出方程并解答．（2）设车位的月租金上涨a 元，则租出的车位数量是（50-5a）个，根据“月租金=每个车位的月租金×车位数”列出函数表达式求解即可．2．【答案】（1）解：根据题意，得()303S x x =-，即所求的函数关系式为2330S x x =-+．∵03039x <-≤，∴710x ≤<，即S 与x 的函数关系式为S=-3x 2+30x(7≤x ＜10)；（2）解：当263m S =时，233063x x -+=，解得17x =，23x =（不合题意，舍去）．∴当7m AB =时，围成花圃的面积为263m ．【解析】【分析】（1）先求出()303S x x =-，再求出710x ≤<，最后作答即可；（2）先求出233063x x -+=，再求解即可。

二次函数的建模 知识归纳：求最值的问题的方法归纳起来有以下几点：1．运用配方法求最值；2．构造一元二次方程，在方程有解的条件下，利用判别式求最值；3．建立函数模型求最值；4．利用基本不等式或不等分析法求最值．一、利用二次函数解决几何面积最大问题1、如图1，用长为18米的篱笆（虚线部分）和两面墙围成矩形苗圃。

(1)设矩形的一边长为x （米），面积为y （平方米），求y 关于x 的函数关系式；(2)当x 为何值时，所围成的苗圃面积最大？最大面积是多少？解：（1）设矩形的长为x （米），则宽为（18- x ）（米）， 根据题意，得： x x x x y 18)18(2+-=-=； 又∵180,0180＜x＜x ＞x ＞∴⎩⎨⎧- （自变量x 的取值范围是关键，在几何类题型中，经常采用的办法是：利用含有自变量的加减代数式的边长来确定自变量的取值范围，例如上式中，18-x ，就是含有自变量的加减代数式，考虑到18-x 是边长，所以边长应该＞0，但边长最长不能超过18，于是有0＜18-x ＜18，0＜x ＜18）（2）∵x x x x y 18)18(2+-=-=中，a= -1＜0，∴y 有最大值， 即当9)1(2182=-⨯-=-=a b x 时， 81)1(41804422max =-⨯-=-=a b ac y 故当x=9米时，苗圃的面积最大，最大面积为81平方米。

点评：在回答问题实际时，一定注意不要遗漏了单位。

2、如图2，用长为50米的篱笆围成一个养鸡场，养鸡场的一面靠墙。

问如何围，才能使养鸡场的面积最大？解：设养鸡场的长为x （米），面积为y （平方米），则宽为（250x-）（米），根据题意，得：x x x x y 2521)250(2+-=-=； 又∵500,02500＜x＜＞x x ＞∴⎪⎩⎪⎨⎧- ∵x x x x y 2521)250(2+-=-=中，a=21-＜0，∴y 有最大值，即当25)21(2252=-⨯-=-=a b x 时，2625)21(42504422max =-⨯-=-=a b ac y 故当x=25米时，养鸡场的面积最大，养鸡场最大面积为2625平方米。

二次函数的解析几何性质及其应用二次函数是数学中常见的一种函数形式，其解析几何性质和应用广泛而深入。

本文将从几何性质和应用两个方面进行阐述。

一、二次函数的解析几何性质1. 函数图像的特征二次函数的一般形式为f(x) = ax^2 + bx + c，其中a、b、c为常数且a≠0。

对于二次函数的图像，其形状为抛物线，具体形状取决于a的正负和大小。

当a>0时，抛物线开口朝上，图像在y轴上方开口；当a<0时，抛物线开口朝下，图像在y轴下方开口。

b和c分别决定了抛物线在x轴方向的平移和y轴方向的平移。

2. 对称性二次函数的图像具有关于直线x = -b/2a的对称性。

这意味着，如果点(x1, y1)在图像上，那么点(x2, y2) = (2(-b/2a)-x1, y1)也在图像上。

这个性质可以通过函数的导数推导得出。

3. 零点和顶点二次函数的零点即为方程f(x) = 0的解，也就是抛物线与x轴的交点。

根据二次函数的解的公式，可以求得零点的坐标。

而二次函数的顶点则是抛物线的最高点（当a<0时）或最低点（当a>0时），其坐标为(-b/2a, f(-b/2a))。

二、二次函数的应用1. 物理学中的抛物线运动抛物线运动是物体在重力作用下的运动轨迹。

由于重力加速度的存在，物体在垂直方向上的运动满足二次函数的形式。

通过分析物体的抛物线轨迹，可以计算出其运动的高度、时间、速度等重要参数。

2. 金融学中的成本和收益分析在金融学中，二次函数常被用于成本和收益的分析。

例如，某公司的生产成本可以表示为二次函数，通过求解该函数的最小值点，可以确定最低成本的生产量。

同样地，某产品的销售收益也可以表示为二次函数，通过求解该函数的最大值点，可以确定最大收益的销售量。

3. 工程学中的曲线设计在工程学中，二次函数常被用于曲线的设计。

例如，公路的水平曲线和立交桥的拱形设计都可以通过二次函数来描述。

通过调整二次函数的参数，可以使得曲线满足工程要求，达到良好的设计效果。

二次函数在几何问题中的应用解析二次函数是一种常见的数学函数形式，它在几何问题中扮演了重要的角色。

本文将探讨二次函数在几何问题中的应用，并对其解析进行分析。

1. 抛物线的性质抛物线是二次函数的图像，其标准形式为y = ax² + bx + c。

在几何中，抛物线具有以下性质：- 对称轴：抛物线的对称轴是一个垂直于x轴的直线，过抛物线的顶点。

对称轴的方程可以通过求抛物线的顶点坐标得到。

- 顶点：抛物线的顶点是曲线的最高点或最低点，可以通过求导数等方法求得。

- 开口方向：抛物线的开口方向由二次项的系数决定。

若a>0，则抛物线开口向上；若a<0，则抛物线开口向下。

- 零点：抛物线与x轴的交点称为零点，可以通过解方程求得。

2. 抛物线在几何中的应用抛物线在几何问题中的应用广泛，以下是其中几个典型的应用示例。

2.1 求解最值问题抛物线的顶点即为其最值点，可通过二次函数的最值性质求解几何问题。

例如，在确定水平距离为d的情况下，求抛物线y = ax² + bx + c的最大值或最小值。

我们可以通过求导数找到使得导数为0的x坐标，再代入函数得到对应的y坐标。

2.2 确定几何形状抛物线的开口方向可以用来确定几何形状。

若抛物线开口向上，则形状类似一个U；若开口向下，则形状类似一个倒置的U。

这在建模物体的运动轨迹、桥梁设计等问题中有广泛的应用。

2.3 优化问题二次函数可以被用于解决优化问题。

例如，当我们需要绘制一个围起来面积最大的矩形时，可以通过分析矩形的边长与面积的关系，建立二次函数模型，并通过求解最值问题得到最大面积。

3. 示例分析假设有一块长为L的铁板，要制作一个没有顶盖的长方体盒子，使得盒子的体积最大。

设长方体的底边宽度为x，高度为h，由此可以得到体积函数V(x) = x( L - 2x )h。

我们可以通过建立函数模型并求解最值问题来解决这个几何问题。

对于函数V(x)，我们首先计算其导数V'(x)，然后令导数为0，解得x = L/4。

二次函数的最值几何应用教学案【教学目标】1．理解二次函数c bx ax y ++=2的图象和性质在平面几何问题中的应用，特别是用来求几何图形面积的最大值或最小值．2．理解二次函数在求解几何问题中的一般方法和步骤． 【重点、难点】重点：二次函数c bx ax y ++=2的图象和性质在平面几何中的应用. 难点：如何将几何问题转化为二次函数的图象和性质问题.【知识要点】1．一次函数的最值：在函数的取值范围的两个端点，考察该函数的最值； 2．二次函数的最值：在函数的取值范围的两个端点考察该函数的最值； 3．函数的最大值与最小值 最大值：()()()()()()().0max 0000x f y x f y x f x f x fx f x x f y ==≤=记作叫做函数都成立，那么不等式处的函数值是在设函数几何解释：(1) 函数图像的最高点，纵坐标最大的值在将一条平行于横坐标的直线从y 坐标。

()()()()()()().0in 0000x f y x f y x f x f x f x f x x f y m ==≥=记作的最小值，叫做函数都成立，那么不等式处的函数值是在设函数 几何解释：(2) 函数图像的最高点，纵坐标最小的值(3) 在将一条平行于横坐标的直线从y 轴的负向向正向平移的过程中，与函数的第一个交点的纵坐标。

【经典例题】例1．求下列函数的最值(自变量范围是R).132)1(2+-=x x y32)2(2++-=x x y例2．已知实数a,b 满足等式5)3(22=+-b a ，求ab的最大值和最小值。

例3．已知二次函数2(1)2y x =--（1）当23x ≤≤时，求函数的最值。

（2）当03x ≤≤时，求函数的最值。

例4．方程()()22160x m x m +-+-=有一根不大于1，另一根不小于1。

（1）求m 的取值范围 （2）求方程两根平方和的最大值与最小值例5．如图，在矩形ABCD 中，,12,6cm BC cm AB ==点P 从点A 开始沿AB 边向点B 以s cm /1的速度移动，点Q 从点B 开始沿BC 边向点C 以s cm /2的速度移动．如果Q P ,分别从B A ,同时出发，设S 表示面积，x 表示移动时间()0>x ．（1）几秒后PBQ ∆的面积等于28cm ；（2）写出D PQ S ∆与x 的函数关系式；（3）写出D PQ S ∆的最小值和最大值，并说明理由．例6．如图,已知ABC ∆的面积为22400厘米,底边BC 长为80厘米,若点D 在BC 边上，E 在AC 边上，F 在AB 边上，且四边形BDEF 为平行四边形,设x BD =厘米,y S BDEF =∆厘米. 求：（1）y 与x 的函数关系式；（2）自变量x 的取值范围； （3）当x 为何值时，y 有最大值？最大值是多少？BQ例7．如图所示，公园要建造圆形喷水池，在水池中央垂直于水面安装一个柱子OA ，O 恰在水面中心，m OA 25.1=，由柱子顶端A 处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路线落下，为使水柱形状较为漂亮，要求设计成水流在离OA 距离为1m 处达到水面最大高度2.25m ．（1）如果不计其他因素，水池的半径至少要多少米？才能使喷出的水不至于落在池外？（2）若水流喷出的抛物线形状与（1）相同，水池的半径为3.5m ，要使水流不落到池外，此时水流最大高度应达多少米？（精确到0.1m ）?例8．如图，二次函数c bx x y ++=2的图象与x 轴只有一个公共交点P ，与y 轴的交点为Q ，过点Q 的直线m x y +=2与x 轴交于点A ，与这个二次函数的图象交于另一点B ，若A P Q B P Q S S ∆∆=3，求这个二次函数的解析式．AO例9．已知二次函数()m x m x y ----=1122的图象与x 轴交于()()21210,0,,0,x x x B x A <<，与y 轴交点C ，且满足COOB AO 211=-．（1）求这个二欠函数的解析式；（2）是否存在着直线b kx y +=与抛物线交于点Q P ,，使y 轴平分CPQ ∆的面积？若存在，求出b k ,满足的条件；若不存在，请说明理由．【课后练习】1．抛物线c bx ax y ++=2与x 轴交于B A ,两点，()k Q ,2是该抛物线上一点，且BQ AQ ⊥，则ak 的值等于（ ）.A 、-1B 、-2C 、2D 、3 2．（扬州市中考时题）已知：039,0=++=+-c b a c b a ，则二次函数c bx ax y ++=2的图象顶点可能在（ ）．A 、第一或第二象限B 、第三或第四象限C 、第一或第四象限D 、第二或第三象限 3．若二次函数c bx ax y ++=2的图象对称于y 轴，那么（ ）．A 、ac b 42=B 、a bx 2-= C 、a b 2= D 、0=b4．用长8m 的铝合金条制成如图形状的矩形窗框，使窗户的透光面积最大， 那么这个窗户的最大透光面积是多少2m （ ）.A 、2564B 、34C 、38D 、45．在一个直角三角形的内部作一个长方形ABCD ，其中AD AB 和分别在两直角边上，若AB 所在直角边为80m ，AD 所在直角边为60m ，则长方形的面积()2m y 与AB 边的长()m x 的函数关系是什么？且当x 取何值时，y 有最大值？（ ）．A 、40,60432x x y +-=B 、40,60432x x y +=C 、40,60432x x y --=D 、40,60432x x y -=6．如图，隧道的截面由抛物线和长方形构成，长方形的长是4m ，宽是2m ，抛物线的解析式为2212+-=x y ，一辆高3m ，宽2mA 、能B 、不能C 、无法确定D 、高为2米时可以通过7．在一个等腰直角三角形的内部作一个矩形ABCD ，其中等腰直角三角形的腰长为20cm,则矩形ABCD 面积的最大值是（ ）.A 、100B 、200C 、300D 、400 二、填空题：1．如果一条抛物线的形状、开口方向都与2312+-=x y 相同，且顶点坐标是()2,4-，则它的解析式是 ．2．抛物线()02≠++=a c bx ax y 经过点()0,1-，则bca +的值是 . 3．若函数322-+=x x y 的的图象与x 轴交于B A ,两点，与y 轴交于C 点， 则ABC ∆的面积等于 ．4．在一个等腰直角三角形内部作一个面积最大的矩形，则这个矩形一定是一个 形．5．隧道的截面是抛物线，且抛物线的解析式为2812+-=x y ，一辆高3米，宽4米的货车 通过该隧道．6．如图所示，在ABC Rt ∆的内部作一个最大的正方形，则此正方形的最大面积为 ． 7．一辆高为4米，宽为2米的货车，通过截面为抛物线m x y +-=221的隧道，则抛物线中的m 的取值范围是 ．三、解答题：如图，F E ,分别是边长为4的正方形ABCD 的边CD BC ,上的点，34,1==CF CE ，直线AB CF 交的延长线于G ，过线段FG 上的一个动点AD HN AG HM H ⊥⊥,作，垂足分别为,,,x HM N M =设矩形AMHN 的面积最大，最大面积是多少？（1）求x y 与之间的函数关系式；（2）当x 为何值时，矩形AMHN 的面积最大，最大面积是多少？CB F GM。