二次函数与几何图形

第八讲 二次函数与几何图形的运用一、知识梳理二次函数与三角形的综合运用：1、求面积及最值2、与三角形的综合运用3、与相似三角形的综合运用4、与四边形的综合运用二、例题例1：如图，已知抛物线y=﹣x 2+mx+3与x 轴交于A ，B 两点，与y 轴交于点C ，点B 的坐标为（3，0）（1）求m 的值及抛物线的顶点坐标．（2）点P 是抛物线对称轴l 上的一个动点，当PA+PC 的值最小时，求点P 的坐标．变式 1 如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0). （1）求该抛物线的解析式；（2）动点P 在x 轴上移动，当△PAE 是直角三角形时，求点P 的坐标.例2、如图，已知点A（0，2），B（2，2），C（﹣1，﹣2），抛物线F：y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P．（1）当抛物线F经过点C时，求它的表达式；（2）设点P的纵坐标为y P，求y P的最小值，此时抛物线F上有两点（x1，y1），（x2，y2），且x1＜x2≤﹣2，比较y1与y2的大小；（3）当抛物线F与线段AB有公共点时，直接写出m的取值范围．例3：在平面直角坐标系xOy中，抛物线y=ax2+bx+2过B（﹣2，6），C（2，2）两点．（1）试求抛物线的解析式；（2）记抛物线顶点为D，求△BCD的面积；（3）若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围．例4：已知二次函数y=ax2﹣2ax+c（a＞0）的图象与x轴的负半轴和正半轴分别交于A、B 两点，与y轴交于点C，它的顶点为P，直线CP与过点B且垂直于x轴的直线交于点D，且CP：PD=2：3（1）求A、B两点的坐标；（2）若tan∠PDB=，求这个二次函数的关系式．例5、如图1，二次函数y1=（x﹣2）（x﹣4）的图象与x轴交于A、B两点（点A在点B的左侧），其对称轴l与x轴交于点C，它的顶点为点D．（1）写出点D的坐标．（2）点P在对称轴l上，位于点C上方，且CP=2CD，以P为顶点的二次函数y2=ax2+bx+c （a≠0）的图象过点A．①试说明二次函数y2=ax2+bx+c（a≠0）的图象过点B；②点R在二次函数y1=（x﹣2）（x﹣4）的图象上，到x轴的距离为d，当点R的坐标为时，二次函数y2=ax2+bx+c（a≠0）的图象上有且只有三个点到x轴的距离等于2d；③如图2，已知0＜m＜2，过点M（0，m）作x轴的平行线，分别交二次函数y1=（x﹣2）（x ﹣4）、y2=ax2+bx+c（a≠0）的图象于点E、F、G、H（点E、G在对称轴l左侧），过点H 作x轴的垂线，垂足为点N，交二次函数y1=（x﹣2）（x﹣4）的图象于点Q，若△GHN∽△EHQ，求实数m的值．三、课堂练习1、如图，在Rt∠AOB的平分线ON上依次取点C，F，M，过点C作DE⊥OC，分别交OA，OB于点D，E，以FM为对角线作菱形FGMH.已知∠DFE＝∠GFH＝120°，FG＝FE.设OC＝x，图中阴影部分面积为y，则y与x之间的函数关系式是 ( )A．y＝32x2 B．y＝3x2 C．y＝23x2 D．y＝33x22、已知抛物线y=2x2+bx+c与直线y=﹣1只有一个公共点，且经过A（m﹣1，n）和B（m+3，n），过点A，B分别作x轴的垂线，垂足记为M，N，则四边形AMNB的周长为．3、直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，当OA⊥OB时，直线AB 恒过一个定点，该定点坐标为．4、如图，抛物线y=ax2+bx﹣经过点A（1，0）和点B（5，0），与y轴交于点C．（1）求抛物线的解析式；（2）以点A为圆心，作与直线BC相切的⊙A，请判断⊙A与y轴有怎样的位置关系，并说明理由；（3）在直线BC上方的抛物线上任取一点P，连接PB、PC，请问：△PBC的面积是否存在最大值？若存在，求出这个值和此时点P的坐标；若不存在，请说明理由．5、如图，在平面直角坐标系中，抛物线y=ax 2+bx+c 的顶点坐标为（2，9），与y 轴交于点A （0，5），与x 轴交于点E 、B ． （1）求二次函数y=ax 2+bx+c 的表达式；（2）过点A 作AC 平行于x 轴，交抛物线于点C ，点P 为抛物线上的一点（点P 在AC 上方），作PD 平行与y 轴交AB 于点D ，问当点P 在何位置时，四边形APCD 的面积最大？并求出最大面积；（3）若点M 在抛物线上，点N 在其对称轴上，使得以A 、E 、N 、M 为顶点的四边形是平行四边形，且AE 为其一边，求点M 、N 的坐标．六、课后作业1、已知抛物线y=ax 2﹣3x+c （a ≠0）经过点（﹣2，4），则4a+c ﹣1= ．2、a 、b 、c 是实数，点A （a+1、b ）、B （a+2，c ）在二次函数y=x 2﹣2ax+3的图象上，则b 、c 的大小关系是b c （用“＞”或“＜”号填空）3、已知二次函数n mx x y ++=2的图像经过点()1,3-P ，对称轴是经过()0,1-且平行于y轴的直线。

数学篇与二次函数有关的几何图形证明题通常较为复杂，需灵活运用数形结合思想，才能顺利解题.这类问题主要考查同学们综合运用二次函数和平面几何图形知识的能力.下面结合几个例题，探讨一下如何求解与二次函数有关的几何图形证明题.一、证明直线平行在解答与二次函数有关的几何图形证明题时，经常会遇到证明两条线段或直线平行的题目，要先根据二次函数的解析式和图象来确定直线上点的坐标，以确定两条直线的位置；然后结合两直线平行的判定定理：如果两条直线被第三条直线所截，同位角相等、内错角相等、同旁内角互补，则两条直线平行，来证明两条直线平行.例1如图1所示，点P 是双曲线y =k 1x上的一动点（x <0，k 1<0），过点P 作y 轴和x轴的垂线，分别交y 轴和x 轴于B 、A 两点，且和双曲线y =k 2x交于F 、E 两点（0<k 1<k 2）.（1）图1中的四边形FOEP 的面积S 1为？（用k 1、k 2表达）（2）图2中，设P 点坐标为（-4,3），求证EF 和AB 平行.图1图2解：（1）略；（2）由题可得E （-4，-k 24），F （k 23，3），∴PA =3，PE =3+k 24，PB =4，PF =4+k 23，∴PA PE =33+k 24=1212+k 2，PB PF =44+k 23=1212+k 2，∴PA PE =PB PF ，又∵∠BPA =∠FPE ，∴△BPA ∽△FPE ，∴∠BAP =∠FEP ，∴EF ∥AB .二、证明三角形全等解答与二次函数有关的全等三角形证明题，大多需要先设出未知数，如二次函数的解析式、点的坐标、角的度数等，并根据二次函数的解析式建立这些未知数之间的关系式，求得两个三角形的边长、内角的大小；再利用勾股定理以及全等三角形的判定定理进行解题.例2如图3所示，在直角坐标系中，正方形CBAO 的边长为2，O 为坐标原点，A 点落在x 轴的正半轴上，C 点落在y 轴的正半轴上.一条抛物线以D 点为顶点并且经过A 点，其中D 点为OC 的中点.（1）求此抛物线的解析式；（2）正方形CBAO 的对角线BO 和抛物线相交于E 点，并且FG 经过E 点且和x 轴垂直，并且交x 轴于F 点，交BC 于G 点.请证明EG 和OB 的长度关系；（3）点H 为抛物线上在正方形CBAO 中的任意一点，线段I J 过点H 和x 轴垂直，并且交x 轴于点I ，交BC 于点J ，点K 在y 轴的正半轴上，并且OH =OK ，求证△IHO ≌△CKJ.图3学思导引如何解答与二次函数有关的几何图形证明题江苏省如皋初级中学杨扬30数学篇解：（1）由题意可得，抛物线的解析式是y =ax 2+b ，把D 点的坐标（0,1）以及A 点的坐标（2,0）代入解析式，便可得出a =-14，b =1.∴抛物线解析式为y =-14x 2+1（2）首先设E 点的坐标为（m ,m ）（0<m <2），因为E 点在正方形CBAO 的对角线BO 上，同时也在抛物线上，由此可得m =-14m 2+1.∴m 1=22-2，m 2=-22-2（舍去）.∴EO =2m =4-22，∴EG =GF -EF =2-m =2-22+2=4-22.∴OE =EG .（3）设点H 的坐标为(p ,q )(0<p <2,0<q <1).∵点H 在抛物线y =-14x 2+1上，∴p 2=4-4q ，∵OH 2=OI 2+HI 2=p 2+q 2=4-4q +q 2=(2-q )2，∴OH =2-q ，OK =OH =2-q ，∴CK =2-(2-q )=q =IH ，∵CJ =OI ，∠HIO =∠JCK =90°，∴△IHO ≌△CKJ .三、证明特殊四边形解答与二次函数有关的特殊四边形证明题，需先根据二次函数的解析式求得四边形各个点的坐标，根据两点间的距离公式求得四边形的边长，并结合二次函数的图象确定各个点的位置；然后根据两直线平行的判定定理判定四边形的对边是否平行，若四边形的对边平行且相等，则该四边形为平行四边形；若该四边形的四条边相等，邻边互相垂直，且对角线互相垂直，则该四边形为正方形；若该四边形的四条边相等，对角线互相垂直，则该四边形为菱形.例3如图4，在直角坐标系xOy 中，点P 是函数y =14x 2在第一象限内的任意一点，A点坐标是（0，1），直线l 交y 轴于点B（0，-1）且和x 轴平行，过点P 作y 轴的平行线交x 轴于点C ，交直线l 于点Q ，连接QA 交x 轴于点H ，直线PH 交y 轴于R .（1）求证点H 是AQ 的中点；（2）求证四边形RQPA 是平行四边形；（3）证明平行四边形RQPA 是菱形.图4解：（1）已知A （0,1），B （0，-1），∴OA =OB ，又∵BQ 和x 轴平行，∴HQ =HA ，由此可得H 是AQ 的中点.（2）根据（1）可知AH =QH ，∠RHA =∠QHP ，∵PQ ∥AR ，∴∠HAR =∠HQP ，∴△HAR ≌△HQP ，∴AR =PQ ，∴四边形RQPA 是平行四边形.（3）设P 的坐标为（m ，14m 2），∵PQ 和y 轴平行，可得Q （m ，-1），PQ =1+14m 2,过P 作PG 垂直于y 轴，垂足为G ，在Rt△GPA 中，AP =AG 2+PG 2===14m 2+1=PQ .RQPA 是菱形.总之，解答与二次函数有关的几何图形证明题，需能够将所学的函数知识、平面几何知识等融会贯通起来，通过数形结合，将问题转化为几何图形的长度、角度问题，以及直线和图形的位置关系问题.学思导引31。

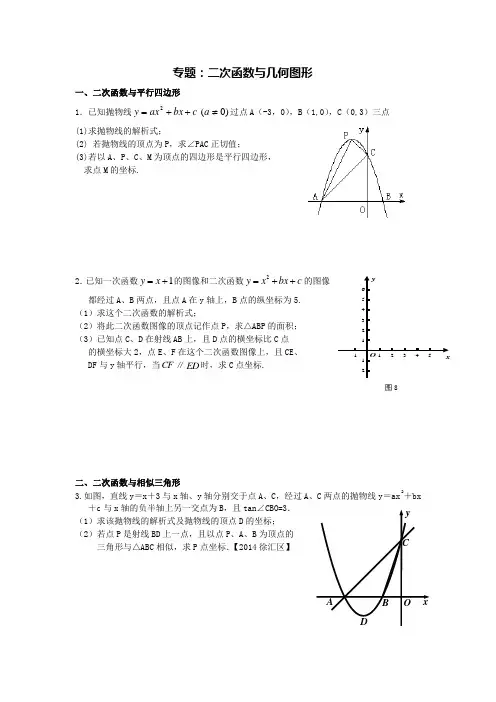
yA xB OCD 专题：二次函数与几何图形 一、二次函数与平行四边形1．已知抛物线c bx ax y ++=2)0(≠a 过点A （-3，0），B （1,0），C （0,3）三点 (1)求抛物线的解析式；(2) 若抛物线的顶点为P ，求∠PAC 正切值；(3)若以A 、P 、C 、M 为顶点的四边形是平行四边形， 求点M 的坐标.2．已知一次函数1y x =+的图像和二次函数2y x bx c =++的图像都经过A 、B 两点，且点A 在y 轴上，B 点的纵坐标为5. （1）求这个二次函数的解析式；（2）将此二次函数图像的顶点记作点P ，求△ABP 的面积； （3）已知点C 、D 在射线AB 上，且D 点的横坐标比C 点 的横坐标大2，点E 、F 在这个二次函数图像上，且CE 、 DF 与y 轴平行，当CF ∥ED 时，求C 点坐标.二、二次函数与相似三角形3.如图，直线y ＝x ＋3与x 轴、y 轴分别交于点A 、C ，经过A 、C 两点的抛物线y ＝ax 2＋bx ＋c 与x 轴的负半轴上另一交点为B ，且tan ∠CBO=3．（1）求该抛物线的解析式及抛物线的顶点D 的坐标； （2）若点P 是射线BD 上一点，且以点P 、A 、B 为顶点的三角形与△ABC 相似，求P 点坐标．【2014徐汇区】12345-1-1-2123456xyO 图8xyOO NC MBA4.已知：在直角坐标系中，直线y=x+1与x 轴交与点A ，与y 轴交与点B ，抛物线21()2y x m n =-+的顶点D 在直线AB 上，与y 轴的交点为C 。

（1）若点C （非顶点）与点B 重合，求抛物线的表达式；（2015杨浦区） （2）若抛物线的对称轴在y 轴的右侧，且CD ⊥AB ，求∠CAD 的正切值； （3）在第（2）的条件下，在∠ACD 的内部作射线CP 交抛物线的对称轴于点P ，使得∠DCP=∠CAD ，求点P 的坐标。

二次函数与几何图形结合题及答案1.如图，已知抛物线21y x =-与x 轴交于A 、B 两点，与y 轴交于点C ．（1）求A 、B 、C 三点的坐标;（2）过点A 作AP ∥CB 交抛物线于点P ，求四边形ACBP 的面积;（3）在x 轴上方的抛物线上是否存在一点M ，过M 作MG ⊥x 轴于点G ，使以A 、M 、G 三点为顶点的三角形与∆PCA 相似．若存在，请求出M 点的坐标；否则，请说明理由． 解：（1）令0y =，得210x -= 解得1x =±令0x =，得1y =- ∴A(1,0)- B(1,0)C (0,1)- ……………………3分（2）∵O A =O B =O C =1 ∴∠BAC =∠AC O=∠BC O=45∵A P ∥CB ， ∴∠P AB =45过点P 作P E ⊥x 轴于E ，则∆A P E 为等腰直角三角形令O E =a ，则P E =1a + ∴P (,1)a a +∵点P 在抛物线21y x =-上 ∴211a a+=-解得12a=，21a=-（不合题意，舍去）∴P E =3……………………………………………………………………………5分∴四边形ACB P 的面积S=12AB •O C +12AB •P E =112123422⨯⨯+⨯⨯=………………………………6分 (3)． 假设存在∵∠P AB =∠BAC =45 ∴P A ⊥AC∵MG ⊥x 轴于点G ， ∴∠MG A =∠P AC =90 在Rt △A O C 中，O A =O C =1 ∴在Rt △P AE 中，AE =P E =3 ∴ 设M 点的横坐标为m ，则M (,m ①点M 在y 轴左侧时，则1m <-(ⅰ) 当∆A MG ∽∆P CA ∵A G=1m --，MG=21m-2322= 解得11m =-（舍去） 223m=（舍去）………9分(ⅱ) 当∆M A G ∽∆P CA 时有AG CA =MGPA即2232=解得：1m =-（舍去） 22m =-∴M (2,3)- ………………………………………………………………………10分② 点M 在y 轴右侧时，则1m >(ⅰ) 当∆A MG ∽∆P CA 时有AG PA =MGCA∵A G=1m +，MG=2m -∴2=解得11m =-∴M 47(,)39………………………11分 (ⅱ) 当∆M A G ∽∆P CA 时有AG CA =MGPA即2232=解得：11m =-（舍去） 24m =∴M (4,15) ………………………………12分∴存在点M ，使以A 、M 、G 三点为顶点的三角形与∆P CA 相似M点的坐标为(2,3)-，47(,)39，(4,15)…………………………………13分2.如图,在平面直角坐标系中，△ABC 是直角三角形,∠ACB =90,AC =BC ,OA =1，OC =4，抛物线2y x bx c =++经过A ，B 两点，抛物线的顶点为D ．（1）求b ,c 的值；（2）点E 是直角三角形ABC 斜边AB 上一动点(点A 、B 除外)，过点E 作x 轴的垂线交抛物线于点F ，当线段EF 的长度最大时，求点E 的坐标；（3）在（2）的条件下：①求以点Ｅ、Ｂ、Ｆ、Ｄ为顶点的四边形的面积；②在抛物线上是否存在一点P ，使△EFP 是以EF 为直角边的直角三角形? 若存在，求出所有点P 的坐标；若不存在，说明理由.解：（1）由已知得：A （-1，0） B （4，5）…………………1分∵二次函数2y x bx c =++的图像经过点A （-1，0）B(4,5) ∴101645b c b c -+=⎧⎨++=⎩ (2)分解得：b=-2c=-3…………………………………………………3分 （2）如２６题图：∵直线AB 经过点A （-1，0） B(4,5)∴直线AB 的解析式为：y=x+1……………………………………4分∵二次函数223y x x =--∴设点E(t ， t+1),则F （t ，223t t --）………………………5分∴EF=2(1)(23)t t t +---………………………………………6分=2325()24t --+∴当32t =时，EF 的最大值=254∴点E 的坐标为（32，52）………………………………7分（3）①如２６题图：顺次连接点E 、B 、F 、D 得四边形ＥＢＦＤ．可求出点F 的坐标（32，154-）,点D 的坐标为（1，-4）SEBFD四边行 = SBEF+ SDEF=12531253(4)(1)242242⨯-+⨯-２６题=758………………………………………………10分 ②如２６题备用图：ⅰ)过点E 作a ⊥EF 交抛物线于点P,设点P(m ,223mm --)则有：25232mm --=解得:1226m =－,2226m+=∴12265)2p －, 22265)2p +ⅱ）过点F 作b ⊥EF 交抛物线于3P ，设3P （n ，223nn --）则有：215423nn --=- 解得：112n=，232n=（与点F重合，舍去）∴3P 11524（，－） 综上所述：所有点P 的坐标：12265()2p －，22265)2p +3P （11524（，－）. 能使△EFP 组成以EF 为直角边的直角三角形．…………………………………… 13分 3.如图,已知二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点，与y 轴交于点P ，顶点为C （1，－2）.（1）求此函数的关系式；（2）作点C 关于x 轴的对称点D ，顺次连接A 、C 、B 、D.若在抛物线上存在点E ，使直线PE 将四边形ABCD 分成面积相等的两个四边形，求点E 的坐标；（3）在（2）的条件下，抛物线上是否存在一点F ，使得△PEF 是以P 为直角顶点的直角三角形？若存在，求出点F 的坐标及△PEF 的面积；若不存在，请说明理由.（1）∵c bx x y ++=2的顶点为C （1，－2），∴2)1(2--=x y ，122--=x xy ． ……………2分（2）设直线PE 对应的函数关系式为b kx y += 由题意，四边形ACBD 是菱形.故直线PE 必过菱形ACBD 的对称中心M ． ………3分由P (0，－1)，M （1，0），得⎩⎨⎧=+-=01b k b ．从而1-=x y ， …5分设E (x ，1-x )，代入122--=x x y ，得1212--=-x xx ．解之得1=x ，32=x ，根据题意，得点E (3，2) …………………………………7分 （3）假设存在这样的点F ，可设F (x，122--x x )．…………………………………8分过点F 作FG ⊥y 轴，垂足为点G . 在Rt △POM和Rt △FGP中，∵∠OMP +∠OPM =90°，∠FPG +∠OPM =90°， ∴∠OMP =∠FPG ，又∠POM =∠PGF，∴△POM ∽△FGP . (9)分∴GFGPOP OM =．又OM =1，OP =1，∴GP =GF ，即xx x =----)12(12．解得01=x ，12=x，根据题意，得F (1，－2)．故点F (1，－2)即为所求．322211221=⨯⨯+⨯⨯=+=MFE MFP PEF S S S △△△．4如图，已知抛物线)0(2≠++=a c bx ax y 的顶点坐标为Q ()1,2-，且与y 轴交于点C ()3,0，与x 轴交于A 、B 两点（点A 在点B 的右侧），点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动（点P 与A 不重合），过点P 作PD ∥y 轴，交AC 于点D ．(1)求该抛物线的函数关系式；(2)当△ADP 是直角三角形时，求点P 的坐标；(3)在问题(2)的结论下，若点E 在x 轴上，点F 在抛物线上，问是否存在以A 、P 、E 、F 为顶点的平行四边形？若存在，求点F 的坐标；若不存在，请说明理由． 解：（1）∵抛物线的顶点为Q （2，－1）∴设()122--=x a y将C （0，3）代入上式，得()12032--=a1=a ∴()122--=x y ，即342+-=x x y …（3分）（2）分两种情况：①当点P 1为直角顶点时,点P 1与点B 重合(如图) 令y =0, 得0342=+-x x 解之得11=x , 32=x∵点A 在点B 的右边, ∴B(1,0), A(3,0)∴P 1(1,0) （5分）②解:当点A 为△APD 2的直角顶点是(如图) ∵OA=OC, ∠AOC= 90, ∴∠OAD 2=45当∠D 2AP 2= 90时, ∠OAP 2=45, ∴AO 平分∠D 2AP 2又∵P 2D 2∥y 轴, ∴P 2D 2⊥AO, ∴P 2、D 2关于x 轴对称设直线AC 的函数关系式为b kx y +=将A(3,0), C(0,3)代入上式得 ⎩⎨⎧=+=bb k 330, ∴⎩⎨⎧=-=31b k ∴3+-=x y ……………（7分） ∵D 2在3+-=x y 上, P 2在342+-=x x y 上,∴设D 2(x ,3+-x ), P 2(x ,342+-x x)∴(3+-x )+(342+-x x)=00652=+-x x , ∴21=x , 32=x (舍)∴当x=2时,342+-=x x y =32422+⨯-=－1 ∴P 2的坐标为P 2(2,－1)(即为抛物线顶点) ∴P 点坐标为P 1(1,0),P 2(2,－1) …………………………………………………（9分） (3)解: 由题(2)知,当点P 的坐标为P 1(1,0)时,不能构成平行四边形……………………（10分）当点P 的坐标为P 2(2,－1)(即顶点Q)时, 平移直线AP(如图)交x 轴于点E,交抛物线于点F. 当AP=FE 时,四边形PAFE 是平行四边形 ∵P(2,－1), ∴可令F(x ,1)∴1342=+-x x解之得: 221-=x , 222+=x ∴F 点有两点,即F 1(22-,1), F 2(22+,1) ……………（13分）。

中考佳题 例析二次函数与几何图形的综合题姓名二次函数与几何图形相结合的综合问题，是近几年来全国各地中考的热点题型.解这类问题的关键就是要善于利用几何图形和二次函数的有关性质和知识，并充分挖掘题目中的隐含条件，以达到解题目的。

一.二次函数与三角形例1.（2006年上海）如图，在直角坐标系中，O 为原点。

点A 在x 轴的正半轴上，点B 在y 轴的正半轴上，t g ∠OAB=2。

二次函数22y x mx =++的图象经过点A 、B ，顶点为D 。

（1）求这个二次函数的解析；（2）将△OAB 绕点A 顺时针旋转900后，点B 落到点C 的位置。

将上述二次函数图像沿y 轴向上或向下平移后经过点C 。

请直接写出点C 的坐标和平移后所得图像的函数解析式； （3）设(2)中平移后所得二次函数图像与y 轴的交点为B 1，顶点为D 1。

点P 在平移后的二次函数图像上，且满足△PBB 1的面积是△PDD 1面积的2倍，求点P 的坐标。

解：（1）由题意，点B 的坐标为()02，， 2OB ∴=，tg 2OAB = ∠，即2OBOA=． 1OA ∴=．∴点A 的坐标为()10，又 二次函数22y x mx =++的图象过点A ，2012m ∴=++．解得3m =-，∴所求二次函数的解析式为232y x x =-+ （2）由题意，可得点C 的坐标为()31，， 所求二次函数解析式为231y x x =-+．（3）由（2），经过平移后所得图象是原二次函数图象向下平移1个单位后所得的图象，那么对称轴直线32x =不变，且111BB DD ==． 点P 在平移后所得二次函数图象上，设点P 的坐标为()231x x x -+，．在1PBB △和1PDD △中，112PBB PDD S S = △△，∴边1BB 上的高是边1DD 上的高的2倍．①当点P 在对称轴的右侧时，322x x ⎛⎫=-⎪⎝⎭，得3x =，∴点P 的坐标为()31，； ②当点P 在对称轴的左侧，同时在y 轴的右侧时，322x x ⎛⎫=- ⎪⎝⎭，得1x =， ∴点P 的坐标为()11-，；③当点P 在y 轴的左侧时，0x <，又322x x ⎛⎫-=- ⎪⎝⎭，得30x =>（舍去）， ∴所求点P 的坐标为()31，或()11-，例2.（2006年桂林）已知，如图，在平面直角坐标系中，⊿ABC 是边长为2的等边三角形，且点A 在y 轴上，点B 、C 在x 轴上。

二次函数与几何图形综合题解题技巧一、求二次函数解析式。

根据y=mx+b，把一元二次方程mx+b=0化为ax+by+c=0的系数a=b，然后通过解方程得出y=mx+b的值，由于不知道b、 a的具体值，可以通过函数与几何图形的综合分析来得到它们的大致范围。

例如，已知点（ 1， 1），（ 3， -3），直线（ x， -3），（ 4， 2）;在(-3， 4)、(-1， 1)处画出一个坐标平面内关于坐标轴对称的二次函数解析式;（ 5， 2）处画出一个关于坐标轴对称的抛物线，使其解析式为y=x+b。

求这些二次函数的表达式。

1。

设二次函数解析式为y=mx+b。

分析：二次函数与一元二次方程有密切联系，解一元二次方程是解二次函数的基础。

设一元二次方程为x+b=0，则根据对称性可得，函数解析式为x+b=mx+c。

2。

设二次函数解析式为y=ax+by+c。

分析： a、 b、 c都是实数，且a>0，b>0。

设函数解析式为x+b=ax+by+c，代入上式可得， y=x+b/c=mx+c/c。

求出二次函数的解析式，即可求出a、 b、 c的值。

3。

设二次函数解析式为y=ax+by+c。

分析：根据对称性，可得y=bx+c， a、 b、c均为实数，且a>0， b>0。

设函数解析式为x+b=bx+c，代入上式可得， y=x+b/c=mx+c/c。

4。

设二次函数解析式为y=ax+by+c。

分析：解方程得y=mx+c，由对称性，得x+c=y+b，代入上式，可得， y=x+b/c。

二、用几何图形解题。

二、用几何图形解题，最好能画出这些图形的图像，再列式解答。

因为几何图形看似复杂，但并不难，常见的如圆的周长、扇形面积、矩形的面积等等。

以下是应用这两种方法解二次函数综合题的例子，供同学们参考： 1。

求出二次函数的解析式，画出抛物线y=mx+b。

分析：首先将点（ 1， 1），（ 3， -3），直线（ x， -3），（ 4， 2） ;在(-3， 4)、(-1， 1)处画出一个坐标平面内关于坐标轴对称的二次函数解析式；再设函数解析式为x+b=mx+c，代入上式得y=mx+c/c。

第三部分函数专题11二次函数与图形几何综合（6大考点）核心考点核心考点一线段问题核心考点二面积问题核心考点三角度问题核心考点四特殊三角形判定问题核心考点五特殊四边形判定问题核心考点六相似三角形判定问题新题速递核心考点一线段问题（2020·吉林长春·统考中考真题）如图，在平面直角坐标系中，点A的坐标为()0,2，点B的坐标为()4,2．若抛物线23()2y x h k=--+（h、k为常数）与线段AB交于C、D两点，且12CD AB=，则k的值为_________．（2020·山东滨州·中考真题）如图，抛物线的顶点为A(h，－1)，与y轴交于点B1(0,)2-，点F(2，1)为其对称轴上的一个定点．（1）求这条抛物线的函数解析式；（2）已知直线l是过点C(0，－3)且垂直于y轴的定直线，若抛物线上的任意一点P(m，n)到直线l的距离为d，求证：PF＝d；（3）已知坐标平面内的点D(4，3)，请在抛物线上找一点Q，使△DFQ的周长最小，并求此时 DFQ周长的最小值及点Q的坐标．1.确定线段长关系式（根据已知线段关系求点坐标）：①先在图中找出对应线段，弄清已知点和未知点；②再联系二次函数和一次函数，设出未知点的坐标，使其只含一个未知数；③继而表示出线段的长度（如果该线段与坐标轴平行的话，则利用横纵坐标相加减确定；如果与坐标轴不平行的话，先转化为有边在与坐标轴平行的三角形中，再利用勾股定理、锐角三角函数或相似确定）．2.线段数量关系问题：根据前面所得的线段长的关系式，结合题干列出满足线段数量关系的方程，解方程求解即可（注意排除不符合题意的数值）．3.线段最值问题：求两条线段和差、三角形周长、四边形周长等一类最值问题，首先联想到“对称性质”，最常见的有以下模型：（1）定直线与两定点①同侧和最小值问题②同侧差最小值问题③同侧差最大值问题④异侧差最大值问题（2）角与定点①一定点与两条直线上两动点问题②两定点与两条直线上两动点问题【变式1】（2020·贵州遵义·统考二模）如图，二次函数图象经过()20A ，，()00O ，且有最小值1-，若A 点关于y 轴的对称点为B 点，过B 作y 轴平行线交抛物线于点C ，在Rt ABC △的斜边AC 上有一动点D ，过D 作DE BC ⊥于E ，DF AB ⊥于F ，则EF 的最小值为（）ABC．D．【变式2】（2021·浙江湖州·模拟预测）如图，已知在平面直角坐标系xOy 中，抛物线C 1：y ＝a 1x 2（a 1≠0）与抛物线C 2：y ＝a 2x 2+bx （a 2≠0）的交点P 在第三象限，过点P 作x 轴的平行线，与物线C 1，C 2分别交于点M ，N ．若PM PN ＝2n ，则12a a 的值是（）A ．2n B ．n ﹣1C ．n D ．11n -【变式3】（2022·山东聊城·统考二模）平面直角坐标系中，将抛物线2y x =-平移得到抛物线C ，如图所示，且抛物线C 经过点()1,0A -和()0,3B ，点P 是抛物线C 上第一象限内一动点，过点P 作x 轴的垂线，垂足为Q ，则OQ PQ +的最大值为______．【变式4】（2021·陕西西安·交大附中分校校考模拟预测）如图，矩形ABCD 中，AB ＝2，BC ＝4，AE 为∠BAD 的角平分线，F 为AE 上一动点，M 为DF 的中点，连接BM ，则BM 的最小值是_____．核心考点二面积问题（2021·山东淄博·统考中考真题）已知二次函数2286y x x =-+的图象交x 轴于,A B 两点．若其图象上有且只有123,,P P P 三点满足123ABPABP ABP S S S m === ，则m 的值是（）A ．1B ．32C ．2D ．4（2021·浙江·统考中考真题）已知抛物线2(0)y ax bx c a =++≠与x 轴的交点为()1,0A 和()3,0B ，点()111,P x y ，()222,P x y 是抛物线上不同于,A B 的两个点，记1P AB △的面积为12,S P AB 的面积为2S ．有下列结论：①当122x x >+时，12S S >；②当122x x <-时，12S S <；③当12221x x ->->时，12S S >；④当12221x x ->+>时，12S S <．其中正确结论的个数是（）A ．1B ．2C ．3D ．4中考数学，最后的三道压轴题，一般都会有一题考察二次函数动点。

二次函数与几何图形综合题解题技巧
函数与几何图形综合题是中学数学中的重要内容，也是考试中的重要考查内容。

在解答函数与几何图形综合题时，要求考生要熟悉函数的性质和几何图形的特征，并熟练掌握解题技巧。

本文就函数与几何图形综合题的解题技巧进行论述，以供考生参考。

首先，考生在解答函数与几何图形综合题时，要仔细阅读题目，弄清题意，明确解题要求。

其次，要熟悉函数的性质，了解函数的变化规律，要熟悉几何图形的特征，如线段、三角形、圆等，以及相关的图形变换，如旋转、缩放等。

然后，要熟悉解函数与几何图形综合题的常用技巧，如分类讨论法、类比法、解析法、图形特征法、函数特征法等。

最后，要做好记号处理，妥善使用符号进行计算，以及绘制相应的函数图像或几何图形，以明确题目要求的结果。

总之，函数与几何图形综合题的解题技巧是考生在完成考试中函数与几何图形综合题的关键，考生应该在正式考试前多加练习，掌握这些解题技巧，以获得更好的考试成绩。

二次函数与几何图形结合与几何图形结合类型一类型一 图形面积有关有关1、 已知已知抛物线抛物线c x ax y ++=22的图象与x 轴交与点A （3,0）和点C ，与y 轴交与点B(0，3) （1） 求抛物线的解析式；（2）在抛物线的对称轴上找一点D ，使得点D 到点B 、C 的距离之和最小，并求出点D 的坐标；（3）在第一象限的抛物线上，是否存在一点P ，使得△ABP 的面积最大？若存在，求出点P 的坐标；若不存在，请说明理由．2、 已知已知抛物线抛物线c bx x y ++=的图象与x 轴的一个轴的一个交点交点为B （5,0），另一个交点为A ，且与y 轴交与点C （0,5）。

（1） 求直线BC 与抛物线的解析式；（2）若点M 是抛物线在x 轴下方图象上的一动点，过点M 作MN ∥y 轴交直线BC 于点N ，求MN 的最大值；（3）在（2）的条件下，MN 取得最大值时，若点P 是抛物线在x 轴下方图象上任意一点，以BC 为边作平行四边形CBPQ ，设平行四边形CBPQ 的面积为S 1，△ABN 的面积为S 2，且S 1=6S 2，求点P 的坐标．3、如图，已知抛物线y=x2+4x+3交x轴于A、B两点，交y轴于点C，抛物线的对称轴交x轴于点E，点B的坐标为（-1，0）．（1）求抛物线的对称轴及点A的坐标；（2）在平面直角坐标系xoy中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由；（3）连接CA与抛物线的对称轴交于点D，在抛物线上是否存在点M，使得直线CM把四边形DEOC分成面积相等的两部分？若存在，请求出直线CM的解析式；若不存在，请说明理由．4、 如图1，已知，已知抛物线抛物线y ＝ax 2＋bx ＋c 经过A(－3，0)，B(1，0)，C(0，3)三点，其顶点为D ，对称轴是，对称轴是直线直线l ，l 与x 轴交于点H ．(1)(1)求该抛物线的求该抛物线的求该抛物线的解析式解析式；(2)(2)若点若点P 是该抛物线对称轴l 上的一个动点，求△上的一个动点，求△PBC PBC 周长的周长的最小值最小值；(3)(3)如图如图2，若E 是线段AD 上的一个动点上的一个动点(E (E 与A 、D 不重合不重合))，过E 点作平行于y 轴的直线交抛物线于点F ，交x 轴于点G ，设点E 的横坐标为m ，△，△ADF ADF 的面积为S ． ①求S 与m 的函数关系式；关系式；②S 是否存在是否存在最大值最大值？若存在，求出最大值及此时点E 的坐标；若不存在，请说明理由．理由．类型二类型二 探究图形形状问题探究图形形状问题1、 如图，已知如图，已知抛物线抛物线经过A （1.0），B （0,3）两点，对称轴是x=-1。

A 0 二次函数与几何图形一、1、线段的和差最值问题例题：已知在抛物线的对称轴上存在一点 △P ，使得 PBC 的周长最小，请求出点 P 的坐标 .2、抛物线与几何图形的面积问题例 1:已知抛物线 y=－x2+2x+3 与 x 轴交于 A,B 两点，其中 A 点位于 B 点的左侧，与 y 轴交于 C 点，顶点为 P练习、如图所示，已知抛物线 y=ax2+bx+c(a≠0)与 x 轴相交于两点 （x1， ） B （x2，0）（x1<x2）与 y 轴负半轴相交于点 C ，若抛物线顶点 P 的横坐标是 1，A 、 B 两点间的距离为 4，且△ABC 的面积为 6。

（1）求点 A 和 B 的坐标 （2）求此抛物线的解析式 （3）求四边形 ACPB 的面积变式（4）在抛物线上（除点 C 外）， 是否存在点 N ，使得 △S NAB = S△ABC， 若 存在，求出点 N 的坐标， 若不存在，请说明理由。

变式（5）设 M （a ，b ）（其中 0<a<3）是抛物线上的一个动点，试求四边形 OCMB 面积的最大值，及此时点 M 的坐标。

练习 2:运动中的面积问题在矩形 ABCD 中，AB=12cm ，BC=6cm ，点 P 沿 AB 边从点 A 出发向 B 以 2cm/秒的速度移动;点 Q 沿 DA 边从点 D 开始向 A 以 1cm/秒的速度移动。

如果 P 、Q 同时 出发，用 t 秒表示移动的时间（0＜t ＜6）那么： (1)设运动开始后第 t 秒钟 后,五边形 QPBCD 的面积为 Scm2,写出 S 与 t 的函数关系式; t 为何值时,S 最小?最小值是多少? (2)求四边形 QAPC 的面积；提出一个与计算结果有关的结论。

①当线段 PQ = AB 时，求 tan ∠CED 的值；二、因动点产生的等腰三角形问题例 12012 年扬州市中考第 27 题如图 1，抛物线 y ＝ax 2＋bx ＋c 经过 A(－1,0)、B(3, 0)、C(0 ,3)三点，直线 l 是抛物线的对称 轴．（1）求抛物线的函数关系式；（2）设点 P 是直线 l 上的一个动点，当△P AC 的周长最小时，求点 P 的坐标； （3）在直线 l 上是否存在点 △M ，使 MAC 为等腰三角形，若存在，直接写出所有符合 条件的点 M 的坐标；若不存在，请说明理由．三、因动点产生的直角三角形问题例 32011 年沈阳市中考第 25 题如图 1，已知抛物线 y ＝x 2＋b x ＋c 与 x 轴交于 A 、B 两点（点 A 在点 B 左侧），与 y 轴交于 点 C(0，－3)，对称轴是直线 x ＝1，直线 BC 与抛物线的对称轴交于点 D ．（1）求抛物线的函数表达式； （2）求直线 BC 的函数表达式；（3）点 E 为 y 轴上一动点，CE 的垂直平分线交 CE 于点 F ，交抛物线于 P 、Q 两点， 且点 P 在第三象限．3 4②当以 C 、D 、E 为顶点的三角形是直角三角形时，请直接写出点 P 的坐标． 温馨提示：考生可以根据第（3）问的题意，在图中补出图形，以便作答．图 1四、因动点产生的平行四边形问题1、已知三个定点，再找一个定点构成平行四边形（平面内有三个点满足）例 1.已知抛物线 y = -ax 2 + 2ax + b 与 x 轴的一个交点为 A(-1,0)，与 y 轴的正半轴交于点 C ．D x N⑴直接写出抛物线的对称轴，及抛物线与x轴的另一个交点B的坐标；⑵当点C在以AB为直径的⊙P上时，求抛物线的解析式；⑶坐标平面内是否存在点M,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形？若存在,请求出点M的坐标；若不存在,请说明理由．2.已知抛物线y=x2-2x+a（a<0）与y轴相交于点A，顶点为M.直线y=12x-a分别与x轴，y轴相交于B，C两点，并且与直线AM相交于点N.(1)填空：试用含a的代数式分别表示点M与N的坐标，则M(，)，N(，)；(2)如图，将△NAC沿y轴翻折，若点N的对应点N′恰好落在抛物线上，AN′与x轴交于点D，连结CD，求a的值和四边形ADCN的面积；(3)在抛物线y=x2-2x+a（a<0）上是否存在一点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出P点的坐标；若不存在，试说明理由.B NCyO N′BP1CyOP2x AM第（2）题AM备用图2、已知两个定点，再找两个点构成平行四边形①确定两定点连接的线段为一边，则两动点连接的线段应和已知边平行且相等）1．已知，如图抛物线y=ax2+3ax+c(a>0)与y轴交于C点，与x轴交于A、B两点，A点在B点左侧。

求顶点坐标时，两种方法，根据不同情况选择快速的方法方法一：公式法求顶点方法二：当得知抛物线上的两个对称点横坐标时，可利用中点求顶点横坐标从而求出抛物线顶点纵坐标当一次函数和二次函数结合时，涉及到线段长短问题，通常两个解题思路思路一：利用两点间距离公式求思路二：通过几何图形进行求解当出现特殊问题时，一定要考虑其特殊性，看有无特殊的方法进行求解27．已知抛物线y =ax 2+x +c （a ≠0）经过A （，0），B （2，0）两点，与y 轴相交于点C ，点D 为该抛物线的顶点．（1）求该抛物线的解析式及点D 的坐标；（2）点E 是该抛物线上一动点，且位于第一象限，当点E 到直线BC 的距离为时，求点E 的坐标；（3）在（2）的条件下，在x 轴上有一点P ，且∠EAO +∠EPO =∠α，当tanα=2时，求点P 的坐标．27．解：（1）∵抛物线y=ax 2+x+c （a ≠0）经过A （﹣1，0），B （2，0）两点，∴，解得． ∴抛物线为y =﹣x 2+x +2①； (1)∴顶点D （，）．………………………………………………………………2 （2）如图，作EN ∥BC ，交y 轴于N ，过C 作CM ⊥EN 于M ，令x =0，得y =2,∴OC =OB =2．∴∠OCB =45°．∵EN ∥BC ，∴∠CNM =∠OCB =45°．∵CM ⊥EN 于M ， ∴∠CNM =∠CMN =45°． ∴MN =CM =． ∴CN =1．∴直线NE 的解析式为：把②代入①，解得∴E （1，2）．（3）过E 作EF ⊥AB 于F1-210420a c a c -+=⎧⎨++=⎩12a c =-⎧⎨=⎩129421x y =⎧⎨=⎩O y x∴tan ∠EOF =2，又∵tan ∠α=2，∴∠EOF =∠α，∵∠EOF =∠EAO +∠AEO =∠α，∠EAO +∠EPO =∠α，∴∠EPO =∠AEO ，∵∠EAO =∠P AE ，∴△AEP ∽△AOE ， (5)∴， ∵AE=，∴AP =8， ∴OP =7， ∴，由对称性可得，∴或．AP AE AE AO=()7,0P ()'5,0P -()7,0P ()5,0-。