五边形形心计算公式
- 格式:doc
- 大小:21.50 KB
- 文档页数:1
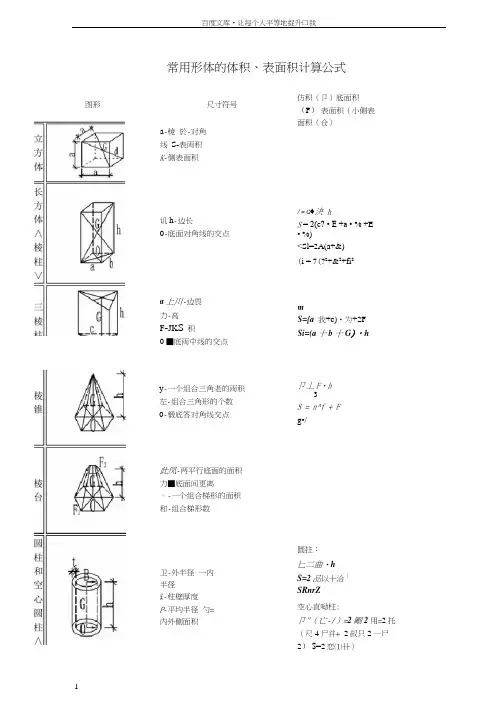
图形常用形体的体积、表面积计算公式尺寸符号a-棱於-对角线S-表両积K-侧表面积讥h-边长0-底面对角线的交点a上川-边畏力-高F-JK S积0 ■底両中线的交点y-一个组合三角老的両积左-组合三角形的个数0-锻底答对角线交点此凤-两平行底面的面积力■底面间更离。
-一个组合梯形的面积和-组合梯形数卫-外半径一內半径£-柱壁厚度P-平均半径勺=内外侧面积仿积(卩)底面积(F)表面积(小侧表面积(仓)/= Q♦決hS = 2(c? • E +a • % +E• %)<Sl=2A(a+&)(i = 7(?2+&2+fi2mS={a我+c)•为+2FSi=(a十b十G)・h卩丄F・h3S = n^f + Fg•/圆拄:匕二曲・hS=2品以十洽1SRnrZ空心直呦柱:卩"(亡-/)=2剛2 用=2托(尺4尸并+ 2叔只2一尸2) $=2恋⑴卄)百度文库•让每个人平等地捉升口我夙一球半径 ①巳-底面半径/腰高兔-球心o 至帝底圆心q 的距离对于抛物线形桶体y = ^-(2D 2+Dd + -d 2)15 4对于回形桶仿 7略(仃+八)a,b,c ■半轴交 叉 柱 体 卩=加(屮一些心3-下底边长上底边长h_上、下底边距离(高)V = -[(2a +勺加+(2甸诃如6 =—[ab+(a +(?})(& 十劣十 ©如6 、常用图形求面积公式图形 尺寸符号而积(F )表而积(S )Q ■中间断面直径H -底直径 I-桶高¥ rU :F =(z 2“疗=0.皿d = 1.414? =1.414#CE^ASAF = CDa = CD (上底边) —朋(下底边)E -高正方 形对角线长方 形—短边 乃-长边 d ■对角线三角 形为-髙周长2久妇c-对应角A,B,®边长F = a d = Qa $ + b?F =毁=丄亦inC2 2 l = ^b + c2平行 四边 形棱边 力-对边间的距离F = c?*^siriaAC^SD .门 =一-——sin#任意 四边 形肉泉2 -对角线 a -对角线夹角正多 边形F = -i?2sin2*2 二竺 2九比_对角线 Q -边a -角F = /sina =2。

托勒密定理五边形证明-概述说明以及解释1.引言1.1 概述托勒密定理是几何学中一个非常重要的定理,它描述了一个特殊的五边形的性质。
这个定理的命名来自于古希腊数学家托勒密,他在其著作《大地与天球的数学基础》中首次提出了这个定理。
托勒密定理主要研究的是一个凸五边形,也就是一个有五个顶点的多边形,且其中的四个顶点都位于一个圆上。
这个定理给出了这个五边形的一条非常重要的性质,即其两对对角线的乘积之和等于两条对边的乘积之和。
具体而言,如果我们设这个五边形的顶点依次为A、B、C、D、E,那么托勒密定理可以表示为AC ×BD + AD ×BC = AB ×CD。
托勒密定理的证明过程非常有趣且具有一定的难度。
它通常使用几何、代数和三角等方法相结合,通过引入辅助线、利用相似三角形关系以及运用勾股定理等工具,从而逐步推导出定理的正确性。
托勒密定理的应用非常广泛。
一方面,在几何学中,托勒密定理是解决五边形相关问题的基础,通过利用这个定理,我们可以推导出许多与五边形有关的性质和公式。
另一方面,托勒密定理在实际应用中也具有一定的价值,如在工程测量中可以用于计算不易直接测量的距离或角度等。
对于托勒密定理的进一步研究也是一个有意义的课题。
目前,已经有许多学者在托勒密定理的基础上进行了延伸和拓展,提出了一些新的数学定理和性质。
同时,随着计算机技术的发展,我们可以利用计算机辅助证明的方法来进一步探索托勒密定理及其相关的数学问题。
综上所述,托勒密定理是几何学中一项重要的成果,它描述了一个特殊五边形的性质。
在本文中,我们将会介绍托勒密定理的定义、性质以及它的证明过程,并探讨其在几何学和实际应用中的意义。
同时,我们还将展望托勒密定理的进一步研究方向,以期能够为数学领域的发展做出更多的贡献。
1.2文章结构文章结构部分的内容可以包括以下内容:文章结构:本文分为引言、正文和结论三个部分。
引言部分主要概述了本文的内容和目的。

高等数学形心计算公式(最新版)目录1.引言:高等数学与形心计算公式的概述2.形心计算公式的定义与性质3.形心计算公式的应用案例4.结论:形心计算公式的重要性与实际意义正文一、高等数学与形心计算公式的概述高等数学是数学中的一个重要分支,它主要涉及到数学分析、代数、几何等多个方面。
在高等数学中,形心计算公式是一种重要的计算工具,广泛应用于各种科学研究和工程实践中。
本文将详细介绍形心计算公式的定义、性质以及应用案例。
二、形心计算公式的定义与性质形心计算公式,又称为形心坐标计算公式,是指在给定一个平面图形或空间图形的情况下,可以计算出该图形形心的数学公式。
形心是指一个图形内部所有点的平均位置,它具有以下性质:1.对于任意一个平面图形,其形心位于该图形内部;2.对于任意一个空间图形,其形心位于该图形内部;3.形心是图形内部所有点的平均位置,具有唯一性。
三、形心计算公式的应用案例形心计算公式在实际应用中具有广泛的应用,下面我们通过两个具体的应用案例来说明形心计算公式的重要性。
案例一:平面图形的形心计算假设有一个边长为 a 的正方形,我们可以通过形心计算公式求出该正方形的形心坐标。
根据公式,正方形的形心坐标为 ((a/2, a/2)。
案例二:空间图形的形心计算假设有一个边长为 a 的立方体,我们可以通过形心计算公式求出该立方体的形心坐标。
根据公式,立方体的形心坐标为 ((a/2, a/2, a/2)。
四、结论:形心计算公式的重要性与实际意义综上所述,形心计算公式是高等数学中一种重要的计算工具,它可以帮助我们求解各种图形的形心坐标。

形心坐标计算公式二重积分形心(centroid)是一个几何物体的重心,它是物体的形状和密度分布的综合体现。
形心坐标是用来描述形心位置的坐标值,它可以通过二重积分的方法计算得到。
二重积分是对二元函数在给定区域上的积分运算。
对于形心坐标的计算,我们可以利用二重积分的定义来求解。
设有一个平面区域D,函数f(x,y)在D上有定义。
我们可以将这个区域D划分为许多小的矩形区域,每个矩形的宽度为Δx,高度为Δy。
那么在每个小矩形区域内部,我们可以取一个任意的点(xi,yi),并计算这个点上函数值f(xi,yi)与矩形面积ΔA的乘积。
然后将每个矩形的乘积相加,即可得到整个区域D上的二重积分。
记D的面积为A,形心坐标为(X,Y),则形心坐标的计算公式为:X = (1/A) ∬[D] x*f(x,y)dxdyY = (1/A) ∬[D] y*f(x,y)dxdy其中符号∬[D]表示对区域D上的积分运算。
实际上,这个二重积分的计算可以通过对x和y分别进行积分的方式得到。
首先对x进行积分,固定y的值,得到新的函数g(y),表示在x方向上的质量或面积分布。
然后对y进行积分,将g(y)与y相乘后对y进行积分,就可以求得形心坐标X。
同样的方法可以求得形心坐标Y。
具体的计算步骤如下:1.对x进行积分,根据具体函数f(x,y)和区域D的形状选择合适的积分方法,得到新的函数g(y)。
2.对y进行积分,将g(y)与y相乘后对y进行积分,得到形心坐标X。
3.同样的方法对y进行积分,得到形心坐标Y。
需要注意的是,对于不规则的区域D和复杂的函数f(x,y),二重积分的计算可能会比较繁琐和复杂。
通常情况下,可以利用数值积分的方法来近似计算形心坐标。
总结起来,形心坐标的计算需要使用二重积分的方法,具体步骤是对函数f(x,y)进行二重积分,并根据定义和区域D的性质获得形心坐标的计算公式。
根据具体情况选择适当的积分方法,并注意处理不规则区域和复杂函数的情况。

半径为r的内接正五边形边心距半径为r的内接正五边形边心距---------------------------------内接正五边形是几何图形中的一种图形,它的定义是一个由五条相等的直线构成的正多边形,且每条边都与另一条边的中点相连。
内接正五边形由半径为r的圆内接而成,其中心距也就是两个顶点之间的距离,是内接正五边形的一个重要参数。
### 一、内接正五边形定义内接正五边形是一种正多边形,它由五条相等的直线构成,且每条边都与另一条边的中点相连。
这种多边形的特点是,所有的外角均为108°,并且它的面积与半径r成正比。
### 二、内接正五边形的特性内接正五边形具有以下特性:1. 所有的外角均为108°;2. 内角均为36°;3. 内接正五边形面积与半径r成正比;4. 每条边心距均相等;5. 每条对角线的长度均为2r;6. 中心到任意一顶点的距离均为r√10/2。
### 三、内接正五边形的计算公式由于内接正五边形的特性,可以用以下公式来求出其中心距:$$a=\sqrt{5r^2-\frac{5}{4}r^2}=\frac{3}{2}r$$其中,a表示中心距,r表示半径。
通过这个公式可以求出内接正五边形的中心距。
### 四、应用场景内接正五边形由于其特殊的几何特性,广泛应用于各行各业。
例如:1. 内接正五边形常用于木工、家具、建筑装饰、建筑加固、建筑几何布局及其他工业领域;2. 内接正五边形在医学领域也有广泛应用,例如在医学成像中常常用于诊断星形血管病变;3. 在数学教学中,内接正五边形常常作为例子用于说明多边形的特性以及几何几率的应用。
### 五、总结以上就是半径为r的内接正五边形的特性以及相关的应用场景。
通过本文可以了解到,内接正五边形不仅具有独特的几何特性,而且也广泛应用于各行各业。

高数求形心坐标公式高等数学中的形心坐标公式是一种求解平面图形形心坐标的方法。
在平面几何中,形心是指一个图形的质心或重心,也就是该图形的所有点的平均位置。
形心坐标公式是通过对图形的面积进行积分来计算形心的坐标。
下面我们将介绍一种求解形心坐标的具体方法。
我们先来了解一下形心的概念。
形心是一个图形的质心或重心,它是该图形的所有点的平均位置。
对于一个平面图形来说,形心是图形的中心点,它与图形的各个边界点的距离之和是最小的。
形心在平面图形的构造和应用中具有重要的作用。
接下来,我们将介绍一种求解平面图形形心坐标的公式。
设图形的边界曲线方程为y=f(x),其中f(x)是一个连续函数。
形心坐标公式可以表示为:x_0 = (1/A) * ∫(x*f(x))dxy_0 = (1/(2A)) * ∫(x^2*f(x))dx其中,A为图形的面积,∫表示积分运算。
形心坐标公式的推导过程相对复杂,我们可以通过几何方法和积分方法来进行推导。
在几何方法中,可以将图形分割成无数个小的面积元素,然后计算每个小面积元素的面积和形心坐标,最后将它们相加平均即可得到形心坐标。
在积分方法中,可以通过对图形的面积进行积分来求解形心坐标。
以一个简单的矩形为例,我们来演示一下形心坐标的计算过程。
设矩形的长为a,宽为b。
根据形心坐标公式,可以得到矩形的形心坐标为:x_0 = (1/ab) * ∫(x*dx) = (1/2) * ay_0 = (1/(2ab)) * ∫(y*dx) = (1/2) * b可以看出,对于矩形来说,形心坐标就是矩形的中心点坐标。
对于其他复杂的图形,我们可以通过形心坐标公式来求解其形心坐标。
通过计算图形的面积和对应的积分,可以得到图形的形心坐标。
形心坐标的计算过程可能会比较繁琐,但是通过高等数学的知识和技巧,我们可以简化计算过程,提高计算效率。
形心坐标在工程和科学研究中具有广泛的应用。
例如,在建筑设计中,通过计算建筑物的形心坐标可以确定建筑物的重心位置,从而保证建筑物的结构稳定性。
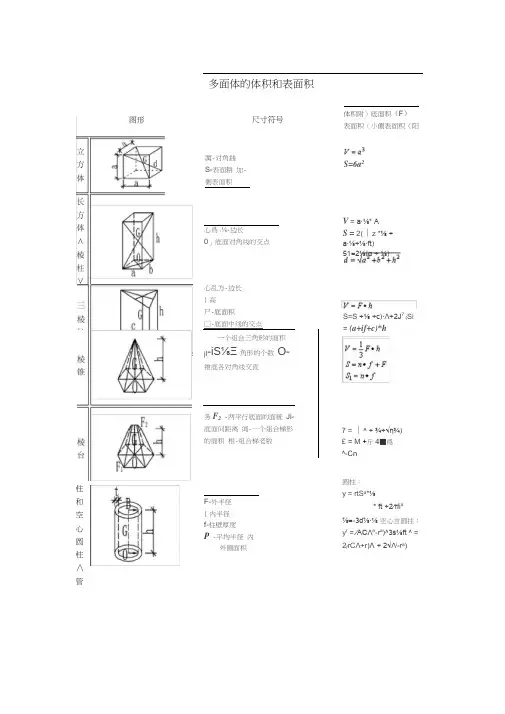
多面体的体积和表面积心乱方-边长 1高 尸-底面积 □-底面中线的交点一个组合三角形的面积jl -iS⅛Ξ角形的个数 O-锥底各对角线交直务F 2 -两平行底面的面粧 Ji-底面间距离 闻-一个爼合梯形的面积 相-组合梯老数7 = ∣^ + ¾÷√η¾) £ = M +斤4■爲 ^-Cn厲-对角銭S-表面耕 加-侧表面积尺寸符号心爲1⅛-边长0」底面对角线的交点体积附)底面积(F ) 表面积(小侧表面积(阳S=6a 2V = a∙⅛* AS = 2(∣z *⅛ +a∙⅛+⅛∙ft)51=2⅛(α + ⅛)柱和 空 心 圆 柱 ∧ 管F-外半径1内半径f-柱壁厚度P -平均半径 内外侧面积圆柱:y = rtS a *⅛* ft +2∕τfi a⅞=-3d⅞∙⅛ 空心言圆拄: y r = ∕ACΛa -r a )^3s⅛ft ^ = 2f rC Λ+r)Λ + 2√Λi -r a )S=S +⅛ +c)∙Λ+2J 7 (Si = (a+if+c)*hVy = ψ∙(j⅞2 3 + √+⅛) 5*1 = KHR+r)I= y ∣(R-r)2+h 2 £ =址十疔(0+/)y = -jιr⅛ =2W44r⅛3 y=^(4ft+rf) = 157f(⅛?+^£斜 线 直 圆 柱 ⅛-≡小高度¾-盘大高度T -底面半径^-^c⅛+⅛>rtf 1∙α+J —) cc≤ αS l - πr(⅛ +¾)r-廐面半径卜母线长+⅛2 =鈕球半径 d ・弓定底11直径A-弓形高一半径d-直径4 3皿'— L.PV = Lf I f =——=0.5236 护36 S=A f tr 2 ==V⅛-球駛的高J--球銭半径d-平切圆直径=曲面面积S-球缺表而稅R -圆球擁平均半径D-圆环体平均半径d-圆怀体截面直径T-匾!环∙⅛⅛⅛面半径尺-球半径①孩-底面半径沟-腰高⅞-⅛∣i<≡Φ底圆⅛3L的距离^ = n fi∖r-¾3¾ -⅛A-rr(^ + A3)护土畋彷-附3⅛ -√D⅛ -3P 478⅛Pr = ^(3⅛+3⅛ + ⅛i) ⅛¾ = 2∕⅛⅛。


网络教程绪论第一章静力学基本概念第二章平面力系第三章重心和形心第四章轴向拉伸与压缩第五章剪切与挤压第六章圆轴的扭转第七章平面弯曲内力第八章梁的强度与刚度第九章强度理论第十章组合变形第十一章质点的运动第十二章刚体基本运动第十三章点的合成运动第十四章刚体平面运动第十五章功和动能定理第十讲重心和形心目的要求:掌握平面组合图形形心的计算。
教学重点:分割法和负面积法计算形心。
教学难点:对计算形心公式的理解。
教学内容:§3-4 重心和形心一、重心的概念:1、重心的有关知识,在工程实践中是很有用的,必须要加以掌握。
2、重力的概念:重力就是地球对物体的吸引力。
3、物体的重心:物体的重力的合力作用点称为物体的重心。
无论物体怎样放置,重心总是一个确定点,重心的位置保持不变。
二、重心座标的公式:(1)、重心座标的公式三、物体质心的坐标公式在重心坐标公式中,若将G=mg,G i=m i g代入并消去g,可得物体的质心坐标公式如下:四、均质物体的形心坐标公式若物体为均质的,设其密度为ρ,总体积为V,微元的体积为V i,则G=ρgV,G i=ρgV i,代入重心坐标公式,即可得到均质物体的形心坐标公式如下:式中V=∑Vi。
在均质重力场中,均质物体的重心、质心和形心的位置重合。
五、均质等厚薄板的重心(平面组合图形形心)公式:令式中的∑A i.x i=A.x c=S y;∑A i.y i=A.y c=S x则S y、S x分别称为平面图形对y轴和x轴的静矩或截面一次矩。
六、物体重心位置的求法工程中,几种常见的求物体重心的方法简介如下:1、对称法凡是具有对称面、对称轴或对称中心的简单形状的均质物体,其重心一定在它的对称面、对称轴和对称中心上。
对称法求重心的应用见下图。
2、试验法对于形状复杂,不便于利用公式计算的物体,常用试验法确定其重心位置,常用的试验法有悬挂法和称重法。
(1)、悬挂法利用二力平衡公理,将物体用绳悬挂两次,重心必定在两次绳延长线的交点上。

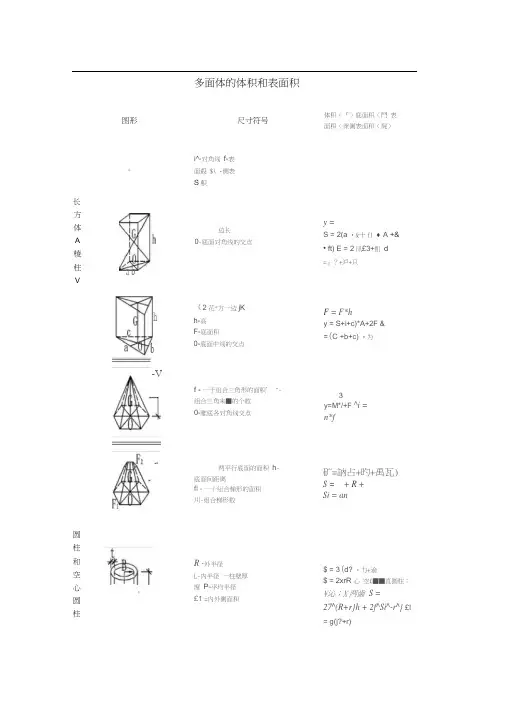
图形多面体的体积和表面积尺寸符号体积(『)底面积(鬥表面积(衆侧表面积(屍)4-i^-对角线f-表面殺 $\ -侧表S积长方体A 棱柱V a b边长0-底面对角线的交点y =S = 2(a •&十fl ♦A +&• ft) E = 2凤£3+酊d=』?+沪+只hb-V(2花*方一边jKh-高F-底面积0-底面中线的交点F = F*hy = S+i+c)*A+2F &=(C +b+c) •为f - 一于组合三角形的面积’ "-组合三角来■的个数0-睢底各对角线交点两平行底面的面积h-底面间距离fl - 一个組合梯形的面积川-组合梯形数3y=M*/+F ^i =n*f矿=訥占+旳+禹瓦)S = + R +Si = an圆柱和空心圆柱qR -外半径L-内半径一柱壁厚度P-平均半径£1 =内外侧面积$ = 3(d? •力+渝$ = 2xrR 心空£■■直圆柱:¥沁;X两歯S =27^(R+r}h + 2f^Si^-r^} £l= g(j?+r)0h-球做的高r-球缺半径d-平切圆直径阳-曲面面秩S-球缺表而羡JZ阳=2寸方=试% +说) /=去(舟-册护=临2「-内)圆环体A 胎V D R-圆球体平均半径D-圆环体平均半径4-圆环体截面克径尸-圆环1$截面半径£ =歸2阳=异氐二翦如g阳球44+^ 带体尺-球半径i孩-底面半径-腰咼片-球心0至希底圆吧q的距离D-中间斷面言径d-底直径』-福高a,b,c-半轴扩=吸调+胡+旳$1 = 2 点£=2価+肌用+甘)对于抛物线世詹体F 二丛(2 £>2+刖+ 3护)15 4对于圆世桶体0=善澎+护)交叉圆柱体r-朗柱半径-圆柱良梯J I』-下磁长矿=-[(加+时由+(221+©竝|h形(31/1-上底边长体J h-上、下底边距离(高)=—\fib+(a+ <31)(9+i>i)+(3i^ 0常用图形求面积公式图形尺寸符号面积(F)表面积(S)F = ^2(7 = 7? = o.77rf ci =1.414(3 -1 414^ZF平行四边形任意四边形正多边形&-长边d-对角绒CAD1 dA尸方-高-棱边Z T-对边间的距离此心-对角线曲-対角錢夹角J? -fl - 3 J,_ F 2 _边fl - ISO 71 <n -辽童妙F -周氐=071F =塑=丄曲gin C3 2, c+b+cF = 6 • Ji = fl •方sin Ct=d£严血0J软Z)=弧皿*2F =—2=ILJ2@5D0£ =陋 肿=3 忆=仞(上底边) 血=屈(下底边J 方一高一半径 d-直徑P -圆周怪a •主轴一半径 「弧长莫-弧$的对应中心角b半径 那长 中」&角 弦长 高R -外半径 F-內半径 D-外直径 d -内直径 f -环宽 务一平均直径F = _ 打 24=07謂护=Dmg%戸 p =niJF= ( n /4) a -bF = —F* $ = =^沖22360s -ISO— L -5 _/nr - ,-J 帆」-0)+滋JJ ■ F ・- O.DIB uF = /r<j?2-F2)兰边瑠b = 0433 四迪磁4 =1000 五边形屁=1.720 咼形心=2.59^ 七边殴7 -3614 八边磁g = 4S28 九边形爲=6.1S2 十边形心)=7砂部 分 圆 环 0R -夕痒径 r -坤免D -夕卜自径 J -内貞径 i -呢R P 」• - d 阡牡直径z -两牛圆心间的距离 d-直径F =*冷- —ff-i-sria) = ?*P180P 十备比琢空 能:见T 废L d/10 2d/10 3d/10 4d/10 5d/10 6d/10 7d/10 P 0.40 0.79 1.18 1.561.912.25 2.55抛 物 线 形&-底边 力-高 「-曲繼L J L 4等 多 边 形"边长屁-系数[指塞边喘的边数。
人教版八年级下册数学五边形知识点总结
1. 五边形的定义和性质
五边形是指具有五条边的多边形。
常见的五边形有正五边形、
等腰五边形和不规则五边形等。
2. 正五边形的性质
正五边形是指五边形的五个边长度相等,五个内角都为108度
的五边形。
正五边形具有以下性质:
- 五个内角都为108度;
- 五个外角都为72度;
- 五个边长相等;
- 对角线相等且相交于中心点;
- 内切圆和外接圆都唯一。
3. 等腰五边形的性质
等腰五边形是指五边形的两个底边和剩余三个边相等的五边形。
等腰五边形具有以下性质:
- 两个底角相等;
- 两个底边相等;
- 对角线相等且相交于中心点;
- 可以内接于一个圆。
4. 不规则五边形
不规则五边形是指五边形的边长和角度都不相等的五边形。
不规则五边形没有明确的性质规律,每个不规则五边形都有其独特的特点。
5. 五边形的周长和面积计算
五边形的周长计算方法是将五个边长相加。
五边形的面积计算方法根据不同的五边形类型有不同的公式,如正五边形的面积公式是 `(边长^2 × √25+10√5) / 4`。
以上是八年级下册人教版数学中关于五边形的知识点总结,希望能对你的研究有所帮助。
凸多边形形心计算公式
凸多边形是一个具有所有内角小于180度的多边形。
形心是凸多边形的一个重要概念,它被定义为凸多边形中所有顶点的坐标的算术平均值。
形心的计算公式可以通过以下步骤得出。
首先,将凸多边形的所有顶点坐标表示为 (x1, y1), (x2, y2), ..., (xn, yn)。
这里,n表示凸多边形的边数。
然后,根据计算公式,形心的 x 坐标可以通过以下公式计算得出:
X = (x1 + x2 + ... + xn) / n
同样地,形心的 y 坐标可以通过以下公式计算得出:
Y = (y1 + y2 + ... + yn) / n
将这两个公式结合起来,我们可以得到凸多边形形心的计算公式为:(X, Y) = ((x1 + x2 + ... + xn) / n, (y1 + y2 + ... + yn) / n)
这个公式可以简单理解为,将凸多边形的所有顶点的 x 坐标和 y 坐标求和后除以顶点的个数,得到形心的坐标。
凸多边形形心的计算公式可以帮助我们确定凸多边形的几何特性,例如确定形心的位置、寻找凸多边形的对称轴等。
它在数学和工程领域中有广泛的应用。
【初中数学】初中数学正五边形的公式定理大全【—正五边形公式定理】正五边形要领:正五边形每个角均为108°,每条边长度相等。
正五边形是旋转对称图形,但不是中心对称图形。
正五边形正五边形的画法常规画法(1)已知边长作正五边形的近似画法①作线段AB等于定长l,并分别以A,B为圆心,已知长l为半径画弧与AB的中垂线交于K。
②取AB的2/3长度延长AK到C,使CK=2/3AB。
③以点C为圆心,已知边长AB为半径画弧,分别与前两弧相交于M,N。
④顺次连接A,B,N,C,M各点即近似作得所要求的正五边形。
(2)民间口诀画正五边形口诀介绍:“九五顶五九,八五两边分”。
画法:①画线段AB=20mm。
②作线段AB的垂直平分线l,垂足为G。
③在l上连续截取GH,HD,使 GH=9.5/5*10mm=19mm,HD=5.9/5*10mm=11.8mm。
④过H作EC⊥HG,在EC上截取HE=HC=8/5*10mm=16mm。
⑤连结DE,EA,AB,BC,CD。
五边形ABCDE就是边长为20mm的近似正五边形。
尺规作图画法1.作线段AB2.作线段AB的垂直平分线HI垂足为H(基本作图)3.以线段AB为一边,作正方形(不会作,看下面小步骤)(1)以点A为圆心,适当长为半径,画弧,交直线AB(看清楚,是直线)于点C、D。
(2)分别以点C、D为圆心,大于二分之一CD长为半径,画弧,两弧交于点E。
(3)过点E作直线AE,并以点A为端点在直线AE上截取线段AF=AB。
(4)以点F、B为圆心,线段AB长为半径,画弧,两弧交于点G。
(5)连结线段FG、BG。
则四边形ABGF为正方形。
4.继续。
以点H为圆心,线段HG长为半径,画弧,交射线HC于点J。
5.分别以点A、J为圆心,线段AB长为半径画弧,两弧交于点K,连结AK BK。
6.作线段HJ的垂直平分线L。
7.以点J为圆心,线段AK长为半径,画弧,交直线L于点M8.再分别以点A。
形心计算公式:∫∫Dxdxdy=重心横坐标×D的面积,∫∫Dydxdy=重心纵坐标×D的面积。
形心是针对抽象几何体而言的,对于密度均匀的实物体,质心和形心重合。
多边形的中心(形心)由下式给出:
关于形心的性质:
1、一个凸对象的几何中心总在其内部。
一个非凸对象的几何中心可能在外部,比如一个环或碗的几何中心不在内部。
2、三角形的重心与三顶点连线,所形成的六个三角形面积相等。
3、顶点到重心的距离是中线的三分之二。
4、重心、外心、垂心、九点圆圆心四点共线。
5、重心、内心、奈格尔点、类似重心四点共线。
6、三角形的重心同时也是中点三角形的重心。