沪科版数学八年级下册 第19章 四边形周滚动练(19.3~19.4)

309309第19章 四边形
周滚动练(19.3~19.4)
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.如图,将矩形纸片ABCD 折叠,使边AB ,CB 均落在对角线BD 上,得折痕BE ,BF ,则∠EBF 的大小为 (C)
A.30°
B.40°
C.45°
D.60°
2.如图,在△ABC 中,点D 在边BC 上(与B ,C 两点不重合),过点D 作DE ∥AC ,DF ∥AB ,分别交AB ,AC 于E ,F 两点,下列说法正确的是 (A)
A.若AD 平分∠BAC ,则四边形AEDF 是菱形
B.若BD=CD ,则四边形AEDF 是菱形
C.若AD ⊥BC ,则四边形AEDF 是矩形
D.若AD 垂直平分BC ,则四边形AEDF 是矩形
3.如图,矩形纸片ABCD 中,AD=4 cm,把纸片沿直线AC 折叠,点B 落在点E 处,AE 交DC 于点O.若AO=5 cm,则AB 的长为(C)
A.6 cm
B.7 cm
C.8 cm
D.9 cm
4.如图,△ABC 中,DE ∥BC ,EF ∥AB ,要判定四边形DBFE 是菱形,还需要添加的条件是
(D)。

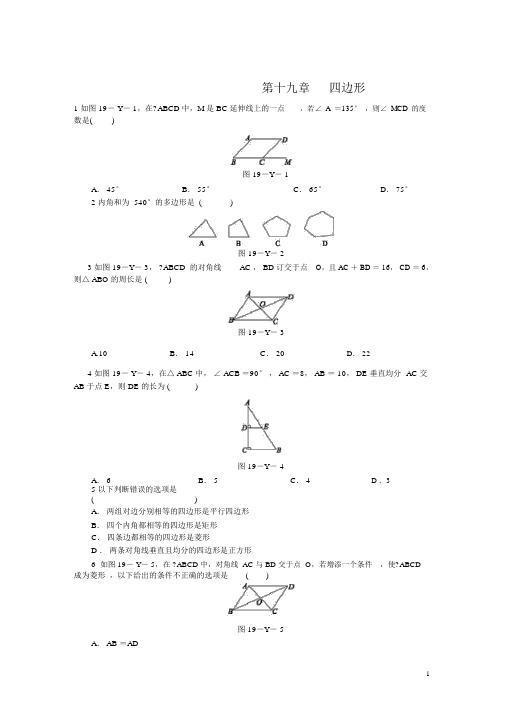
第十九章四边形1 如图 19－ Y－ 1，在?ABCD 中，M 是 BC 延伸线上的一点，若∠ A＝135° ，则∠ MCD的度数是()图 19－Y－ 1A． 45°B． 55°C． 65°D． 75°2 内角和为 540°的多边形是 ( )图 19－Y－ 23 如图 19－Y－ 3， ?ABCD 的对角线AC ， BD 订交于点O，且 AC ＋ BD ＝ 16， CD ＝ 6，则△ ABO 的周长是 ()图 19－Y－ 3A.10B． 14C． 20D． 224 如图 19－ Y－ 4，在△ ABC 中，∠ ACB ＝90°， AC ＝8， AB ＝ 10， DE 垂直均分AC 交AB 于点 E，则 DE 的长为 ()图 19－Y－ 4A． 6 B． 5 C． 4 D ．35 以下判断错误的选项是( )A．两组对边分别相等的四边形是平行四边形B．四个内角都相等的四边形是矩形C．四条边都相等的四边形是菱形D ．两条对角线垂直且均分的四边形是正方形6如图 19－ Y－ 5，在 ?ABCD 中，对角线 AC 与 BD 交于点 O，若增添一个条件，使?ABCD成为菱形，以下给出的条件不正确的选项是()图 19－Y－ 5A． AB ＝AD1B． AC ⊥BDC． AC ＝BDD ．∠ BAC ＝∠ DAC7 如图 19－Y－ 6，在 ?ABCD 中，AB ＞ AD ，按以下步骤作图：以点 A 为圆心，小于 AD1的长为半径画弧，分别交AB，AD于点E，F，再分别以点E，F 为圆心，大于2EF 的长为半径画弧，两弧交于点 G.作射线 AG 交 CD 于点 H，则以下结论中不可以由条件推理得出的是()图 19－Y－ 6A． AG 均分∠ DABB． AD ＝DHC． DH ＝BCD．CH＝DH8如图 19－Y－ 7，在?ABCD 中， AB ＝6， BC＝ 8，∠ C 的均分线交 AD 于点 E，交 BA的延伸线于点F，则 AE ＋AF 的值等于 ()图 19－Y－ 7A． 2B． 3C． 4D ． 69 如图 19－Y－8，在矩形 ABCD 中(AD ＞AB) ，点 E 是 BC 上一点，且 DE＝DA，AF⊥ DE ，垂足为 F.在以下结论中，不必定正确的选项是()图 19－Y－ 8A．△ AFD ≌△ DCE1B． AF ＝2ADC． AB ＝AFD．BE＝AD －DF10如图 19－ Y－ 9，矩形 ABCD 的对角线 AC 与 BD 订交于点 O， CE∥BD ， DE∥ AC ，AD ＝ 2 3， DE＝ 2，则四边形OCED 的面积为 ()2图 19－Y－ 9A．2 3B． 4C．4 3D ． 811 如图 19－ Y－ 10，在 Rt△ ABC 中，E 是斜边 AB 的中点．若 AB ＝ 10，则 CE ＝________．图 19－ Y－ 1012如图 19－ Y－ 11，在 ?ABCD 中，BE ⊥ AB 交对角线 AC 于点 E，若∠ 1＝ 20°，则∠ 2 的度数为 ________．图 19－Y－ 1113 已知矩形的对角线AC 与 BD 订交于点 O，若 AO ＝ 1，那么 BD ＝ ________．图 19－ Y－ 1214如图 19－Y－ 13 所示，在 ?ABCD 中，∠ C＝40°，过点 D 作 AD 的垂线，交 AB 于点E，交 CB 的延伸线于点 F，则∠ BEF 的度数为 ________．图 19－ Y－ 1315如图 19－ Y－ 14，在矩形 ABCD 中，AB ＝ 3，对角线 AC ， BD 订交于点 O， AE 垂直均分 OB 于点 E，则 AD 的长为 ________．图 19－ Y－ 1416如图 19－ Y－ 15，菱形 ABCD 的面积为 120 cm2，正方形 AECF 的面积为 50 cm2，则菱形的边长为 ________cm.图 19－ Y－ 1517.如图 19－Y－ 16，在正方形ABCD 中，对角线 AC 与 BD 订交于点O， E 为 BC 上一3点，CE ＝5， F 为 DE 的中点．若△CEF 的周长为18，则 OF 的长为 ________．图 19－ Y－ 1618如图 19－Y－ 17，已知 BD 是△ ABC 的角均分线，点 E， F 分别在边 AB ， BC 上，ED ∥ BC， EF∥ AC. 求证： BE ＝ CF.图 19－ Y－ 1719如图 19－ Y－18，在 Rt△ ABC 中，∠B ＝90°，点 E 是 AC 的中点，AC ＝ 2AB ，∠BAC 的均分线AD 交 BC 于点 D ，作 AF ∥ BC ，连结 DE 并延伸交AF 于点 F，连结 FC.求证：四边形ADCF 是菱形．图 19－ Y－ 1820如图 19－Y－ 19，AC 为矩形 ABCD 的对角线，将边 AB 沿 AE 折叠，使点 B 落在AC 上的点 M 处，将边 CD 沿 CF 折叠，使点 D 落在 AC 上的点 N 处．(1)求证：四边形 AECF 是平行四边形；(2)若 AB ＝ 6， AC ＝ 10，求四边形 AECF 的面积．4图 19－ Y － 19[ 分析 ] 设多边形的边数是 n ，则 (n － 2) ·180°＝ 540°， 解得 n ＝ 5.应选 C.[分析 ] ∵四边形ABCD 是平行四边形 ，∴ AO ＝ CO ，BO＝DO ，DC ＝ AB ＝ 6.∵ AC＋ BD ＝16， ∴ AO ＋ BO ＝ 8，∴△ ABO 的周长是 14.1． A 2． C 3．B54． D [ 分析 ] ∵在 Rt △ ACB 中， ∠ ACB ＝ 90°， AC ＝ 8， AB ＝ 10，∴ BC ＝ 6.又∵ DE 垂直均分 AC 交 AB 于点 E ， ∴ DE 是△ ACB 的中位线 ， ∴DE ＝1BC ＝ 3.2 5．D [ 分析 ] A 选项，两组对边分别相等的四边形是平行四边形 ，正确，故本选项错误； B 选项 ，四个内角都相等的四边形是矩形 ，正确，故本选项错误； C 选项 ，四条边都相等的四边形是菱形，正确，故本选项错误；D 选项 ，两条对角线垂直且均分的四边形是正方形，错误 ，应当是菱形 ，故本选项正确．6． C [ 分析 ] A 选项 ，依据菱形的定义可得 ，当 AB ＝ AD 时 ?ABCD 是菱形； B 选项 ，依据对角线相互垂直的平行四边形是菱形即可判断 ，当 AC ⊥BD 时，?ABCD是菱形；C 选项 ，对角线相等的平行四边形是矩形 ，不必定是菱形 ，命题错误；D 选项 ，∠ BAC ＝∠ DAC 时，∵在 ?ABCD 中，AD ∥ BC ，∴∠ ACB ＝∠ DAC ，∴∠ BAC ＝∠ ACB ， ∴AB ＝ AC ， ∴ ?ABCD 是菱形．7 ． D [ 分析 ] 依据作图的方法可得 AG 均分∠ DAB. ∵ AG 均分∠ DAB ， ∴∠ DAH ＝ ∠ BAH. ∵ CD ∥AB ，∴∠ DHA ＝∠ BAH ，∴∠ DAH ＝∠ DHA ，∴ AD ＝DH ，BC ＝DH ，应选 D.8．C [分析 ] ∵四边形 ABCD 是平行四边形 ， ∴AB ∥ CD ，AD ＝ BC ＝ 8，CD ＝ AB ＝6， ∴∠ F ＝∠ DCF.∵∠ C 的均分线为 CF ，∴∠ FCB ＝∠ DCF ， ∴∠ F ＝∠ FCB ，∴ BF ＝BC ＝8，同理 DE ＝CD ＝6，∴ AF ＝ BF － AB ＝ 2，AE ＝ AD － DE ＝2，∴ AE ＋AF ＝4.9． B [分析 ] A 项，由四边形 ABCD 是矩形 ， AF ⊥DE 可得∠ C ＝∠ AFD ＝ 90°， AD ∥ BC ， ∴∠ ADF ＝∠ DEC. 又∵ DE ＝ AD ， ∴△ AFD ≌△ DCE(AAS) ，故 A 项正确；B 项，∵∠ ADF 不必定等于 30°，∴在直角三角形 ADF 中，AF 不必定等于 AD 的一半 ，故 B 项错误；C 项，由△ AFD ≌△ DCE ，可得 AF ＝ CD ，由四边形 ABCD 是矩形 ，可得 AB ＝ CD ，∴ AB ＝ AF ，故 C 项正确；D 项，由△ AFD ≌△ DCE ，可得 CE ＝ DF.由四边形 ABCD 是矩形 ，可得 BC ＝ AD. 又∵ BE＝ BC －EC ，∴ BE ＝ AD － DF ，故 D 项正确．10． A [ 分析 ] 连结 OE ，与 DC 交于点 F.∵四边形ABCD 为矩形 ， ∴OA ＝ OC ， OB ＝OD ，且 AC ＝ BD ，即 OA ＝ OB ＝ OC ＝ OD.∵ OD ∥ CE ，OC ∥ DE ，∴四边形 ODEC 为平行四边形．∵ OD ＝OC ， ∴四边形 ODEC 为菱形 ， ∴DF ＝ CF ， OF ＝ EF ， DC ⊥ OE.∵ DE ∥ OA ，且 DE ＝ OA ，∴四边形 ADEO 为平行四边形．∵AD ＝23，DE ＝2，∴OE ＝23，即 OF ＝ EF ＝ 3.在 Rt △ DEF 中，依据勾股定理得 DF ＝ 4－ 3＝ 1，即 DC ＝ 2，则 S 菱形 ODEC ＝ 1OE ·DC2 1＝2×23× 2＝2 3.11． 512． 110° [分析 ] ∵四边形 ABCD 是平行四边形 ， ∴ AB ∥CD ，∴∠ BAE ＝∠ 1＝ 20° .∵ BE ⊥AB ， ∴∠ ABE ＝90° ，∴∠ 2＝∠ BAE ＋∠ ABE ＝ 110°.13． 2 [分析 ] 在矩形 ABCD 中，∵角线 AC 与 BD 订交于点 O ， AO ＝ 1， ∴ AO ＝ CO6＝ BO ＝DO ＝ 1，∴ BD ＝ 2.14．50° [分析 ] ∵四边形 ABCD 是平行四边形 ，∴ DC ∥AB ，∴∠ C ＝∠ ABF. 又∵∠ C＝ 40°， ∴∠ ABF ＝ 40° .∵ EF ⊥ AD ，AD ∥ BC ， ∴EF ⊥ BF ，∴∠ F ＝ 90° ，∴∠ BEF ＝ 90° － 40°＝ 50° .15． 3 3 [分析 ] ∵四边形 ABCD 是矩形 ，∴ OB ＝ OD ，OA ＝ OC ，AC ＝ BD ，∴ OA ＝ OB.∵AE 垂直均分 OB ， ∴AB ＝ AO ， ∴OA ＝ AB ＝ OB ＝ 3， ∴ BD ＝ 2OB ＝ 6， ∴AD ＝ BD 2－AB 2＝ 62－ 32＝ 3 3.16． 13[分析 ] 由于正方形 AECF 的面积为 50 cm 2，因此 AC ＝ 2× 50＝ 10(cm)．由于菱 形 ABCD 的 面 积 为 120 cm 2， 所 以 BD ＝2× 120 ＝ 24(cm) ， 所 以 菱 形 的 边 长 ＝10 （10）2＋（24） 2＝ 13(cm)．2217. 7[分析 ] ∵ CE ＝ 5，△CEF 的周长为 18，∴ CF ＋ EF ＝ 18－ 5＝13.∵ F 为 DE 的中点 ，2∴ DF ＝ EF.∵∠ BCD ＝ 90° ， ∴ CF ＝ 1DE ， ∴ EF ＝ CF ＝ 1DE ＝ 6.5， ∴ DE ＝ 2EF ＝ 13， ∴CD2 2 ＝ DE 2－CE 2＝ 132－ 52＝ 12.∵四边形 ABCD 是正方形 ，∴BC ＝ CD ＝ 12，O 为 BD 的中点 ，11 7 .∴ OF 是△ BDE 的中位线 ， ∴OF ＝ (BC － CE)＝ (12－ 5)＝ 2 2 218． 证明： ∵ ED ∥ BC ， EF ∥AC ， ∴四边形 EFCD 是平行四边形 ，∴ DE ＝ CF.∵ BD 均分∠ ABC ， ∴∠ EBD ＝∠ DBC. ∵ DE ∥BC ，∴∠ EDB ＝∠ DBC ， ∴∠ EBD ＝∠ EDB ， ∴ BE ＝ED ，∴BE ＝ CF. 19． 证明： ∵ AF ∥ CD ， ∴∠ AFE ＝∠ CDE. ∵点 E 是AC 的中点， ∴ AE ＝ CE.在△ AFE 和△ CDE 中，∠ AFE ＝∠ CDE ，∠ AEF ＝∠ CED ，AE ＝ CE ，∴△ AEF ≌△ CED(AAS) ，∴ AF ＝ CD. ∵AF ∥CD ，∴四边形 ADCF 是平行四边形．∵∠ B ＝ 90° ， ∠ACB ＝30° ， ∴∠ CAB ＝60° . ∵ AD 均分∠ CAB ，∴∠ DAC ＝∠ DAB ＝ 30°＝∠ ACD ， ∴ DA ＝DC ，∴四边形 ADCF 是菱形．20．解： (1)证明：由折叠可知 AM ＝ AB ，CN ＝ CD ，∠ FNC ＝∠ D ＝ 90° ，∠ AME ＝∠ B ＝ 90°，∴∠ ANF ＝ 90° ， ∠CME ＝ 90° .∵四边形 ABCD 为矩形 ，7∴AB ＝CD，AD ∥BC，∴AM ＝CN ，∠ FAN ＝∠ ECM ，∴AM －MN ＝ CN－ MN ，即 AN＝CM.在△ ANF 和△ CME 中，∠FAN ＝∠ ECM ，AN ＝CM ，∠ANF ＝∠ CME ，∴△ ANF ≌△ CME(ASA) ，∴AF ＝ CE.又∵ AF∥ CE，∴四边形 AECF 是平行四边形．(2)∵AB ＝6，AC ＝10，∴BC ＝ 102－62＝ 8，设 CE＝ x，则 EM＝ 8－ x, CM ＝ 10－6＝ 4，在 Rt△ CEM 中， (8－x) 2＋ 42＝x2，解得 x＝ 5，∴四边形AECF 的面积为EC·AB ＝ 5× 6＝ 30.8。

沪教版八年级下册第19章四边形练习题一、选择题1. 用两块完全重合的等腰直角三角形纸片拼下列图形：①平行四边形（不包括菱形，正方形）②矩形（不是正方形）③正方形④等边三角形⑤等腰直角三角形，一定能拼成的图形是……………………………………………（）A. ①②③B. ①③⑤C. ②③⑤D. ①③④⑤2. 用两块完全相同的直角三角形拼下列图形：①平行四边形②矩形③菱形④正方形⑤等腰三角形⑥等边三角形，一定能拼成的图形是…（）A. ①④⑤B. ②⑤⑥C. ①②③D. ①②⑤3. 用长为100cm的金属丝制成一个矩形框子，框子的面积不可能是…（）A. 325cmB. 500cmC. 625cmD. 800cm﹡﹡4.剪掉多边形的一个角，则所成的新多边形的内角和…………………（）A. 减少180°B. 增加180°C. 减少所剪掉的角的度数D. 增加180°或减少180°或不变5. 如图，△BDC′是将矩形纸片ABCD沿对角线BD折叠得到的，图中（包括实线、虚线在内）共有全等三角形……………………………………………（）A. 2对B. 3对C. 4对D. 5对6. 2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图）。

如果大正方形的面积是13，小正方形的面积是1，直角三角形较短直角边为a，较长直角边为b，那么（ a+b）2的值为……………………………………………………………（）A. 13B.19C.25D.1697. 如图，平行四边形ABCD中，∠A的平分线AE交CD于E，AB=5，BC=3，则EC长…………………………………………………………………………（）A. 1B. 1.5C. 2D. 38. 一个多边形的内角和为540°，则其对角线的条数是……………（）A. 3条B. 5条C. 6条D. 12条9. 一个多边形每一个顶点取一个外角，这些外角中钝角最多的个数是（）A. 1个B. 2个C. 3个D. 4个10. 国旗上每个五角星……………………………………………………（）A.是中心对称图形而不是轴对称图形B.是轴对称图形而不是中心对称图形C.即是中心对称图形又是轴对称图形D.即不是中心对称图形又不是轴对称图形11. 等腰梯形的两底之差等于腰长，则腰与下底的夹角为……………（）A. 120°B. 60°C. 45°D. 135°12. 当一个多边形的边数增加1时，它的外角和增加…………………（）A. 180°B. 0°C. n·180°D. 360°13. 两个多边形的边数之比为2:1，内角之比为8:3，则她们的边数之和为…………………………………………………………………………………（） A. 15 B. 12 C. 21 D. 18二、填空题1. 依次连接等腰梯形的各边中点所成的四边形是________。

第19章四边形周滚动练(19.1~19.2)(时间:45分钟满分:100分)一、选择题(每小题4分,共32分)1.已知一个多边形的内角和是900°,则这个多边形是(C)A.五边形B.六边形C.七边形D.八边形2.如图,在▱ABCD中,MB是∠ABC的平分线,交CD于点M,且MC=2,▱ABCD的周长是14,则DM等于(B)A.4B.3C.2D.13.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为(C)A.4B.6C.8D.104.直角三角形两直角边边长分别为6和8,则连接这两条直角边中点的线段长为(B)A.10B.5C.4D.35.在平面直角坐标系中,▱ABCD的顶点A,B,C的坐标分别是(0,0),(3,0),(4,2),则顶点D的坐标为(C)A.(7,2)B.(5,4)C.(1,2)D.(2,1)6.如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是(B)A.7B.10C.11D.127.如图,在▱ABCD中,AE⊥BC于点E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则▱ABCD的周长为(A)A.4+2B.12+6C.2+2D.2+2或16+68.如图,▱ABCD的对角线AC和BD相交于点O,AE⊥BC,垂足为E,AB=4,AC=6,BD=10,则AE的长为(D)A. B.C. D.二、填空题(每小题5分,共20分)9.一个多边形的内角和是外角和的3倍,这个多边形的对角线有20条.10.如图,在平行四边形ABCD中,AB=,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为3.11.在▱ABCD中,AD=BD,BE是AD边上的高,∠EBD=20°,则∠A的度数为55°或35°.12.如图,在▱ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE.下列结论正确的是①②③.(写出正确结论的序号)①BO=OH;②DF=CE;③DH=CG;④AB=AE.三、解答题(共48分)13.(8分)已知平行四边形ABCD中,∠B=4∠A,求∠C的度数.解:∵四边形ABCD是平行四边形,∴∠C=∠A,BC∥AD,∴∠A+∠B=180°.∵∠B=4∠A,∴∠A=36°,∴∠C=∠A=36°.14.(8分)如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.(1)求∠APB的度数;(2)如果AD=5 cm,AP=8 cm,求△APB的周长.解:(1)∵四边形ABCD是平行四边形,∴AD∥CB,AB∥CD,∴∠DAB+∠CBA=180°,又∵AP和BP分别平分∠DAB和∠CBA,∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,∴在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°.(2)∵AP平分∠DAB,AB∥CD,∴∠DAP=∠PAB=∠DPA,∴△ADP是等腰三角形,∴AD=DP=5 cm,同理PC=CB=5 cm,即AB=DC=DP+PC=10 cm,在Rt△APB中,AB=10 cm,AP=8 cm,∴BP==6 cm,∴△APB的周长=AB+AP+BP=24 cm.15.(10分)如图所示,如果在▱ABCD中∠BAD的平分线交BC于点E,且AE=BE,求▱ABCD 各内角的度数.解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠AEB.∵AE=BE,∴∠B=∠EAB,又∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠B=∠BAE=∠AEB=60°,∴∠D=60°,∠BAD=∠C=120°.16.(10分)如图,在平行四边形ABCD中,E,F分别在AD,BC边上,且AE=CF.求证:(1)△ABE≌△CDF;(2)四边形BFDE是平行四边形.证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,∠A=∠C.又∵AE=CF,∴△ABE≌△CDF.(2)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC.又∵AE=CF,∴AD-AE=BC-CF,即DE=BF.∵AD∥BC,∴DE∥BF,∴四边形BFDE是平行四边形.17.(12分)如图,在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ADE≌△CBF;(2)连接AC,若AC与BD相交于点O,求证:AO=CO.证明:(1)∵AE⊥BD,CF⊥BD,∴∠AED=∠BFC=90°.∵BE=DF,∴DF-EF=BE-EF,即BF=DE.在Rt△ADE和Rt△CBF中,∴△ADE≌△CBF.(2)由(1)知△ADE≌△CBF,∴AE=CF,∵∠AEO=∠CFO=90°,∴AE∥CF,∴四边形AFCE是平行四边形,∴AO=CO.。

沪科版八年级数学下册第19章四边形章节练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、若一个正多边形的每一个外角都等于36°，则这个正多边形的边数是（）A．7 B．8 C．9 D．102、如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（）A．2.5 B．C D3、如图，小明从点A出发沿直线前进10m到达点B，向左转30，后又沿直线前进10m到达点C，再向左转30°后沿直线前进10m到达点．．．照这样走下去，小明第一次回到出发点A，一共走了（）米．A．80 B．100 C．120 D．1404、一个多边形纸片剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的边数为（）A．14或15或16 B．15或16或17 C．15或16 D．16或175、在Rt△ABC中，∠C＝90°，若D为斜边AB上的中点，AB的长为10，则DC的长为（）A．5 B．4 C．3 D．26、平行四边形ABCD中，60∠=︒，则CA∠的度数是（）A．30B．60︒C．90︒D．120︒∠+∠的度数是（）7、如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中αβA．180°B．220°C．240°D．260°8、一个多边形每个外角都等于36°，则这个多边形是几边形（）A．7 B．8 C．9 D．109、在菱形ABCD中，对角线AC、BD相交于点O，AB＝5，AC＝6，过点D作AC的平行线交BC的延长线于点E，则△BDE的面积为（）A．22 B．24 C．48 D．4410、绿丝带是颜色丝带的一种，被用来象征许多事物，例如环境保护、大麻和解放农业等，同时绿丝带也代表健康，使人对健康的人生与生命的活力充满无限希望．某班同学在“做环保护航者”的主题班会课上制作象征“健康快乐”的绿丝带（丝带的对边平行且宽度相同），如图所示，丝带重叠部分形成的图形是（）A．矩形B．菱形C．正方形D．等腰梯形第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在矩形ABCD中，AB＝3，BC＝4，点P是对角线AC上一点，若点P、A、B组成一个等腰三角形时，△PAB的面积为___________．2、一个矩形的两条对角线所夹的锐角是60°，这个角所对的边长为10cm，则该矩形的面积为_______．3、如图在正方形ABCD中，∠EAF的两边分别交CB、DC延长线于E、F点且∠EAF＝45°，如果BE＝1，DF＝7，则EF＝__．4、正方形的一条对角线长为4，则这个正方形面积是_________．5、如图，正方形ABCD内有一等边三角形BCE，直线DE交AB于点H，过点E作直线GF⊥DH交BC于点G，交AD于点F．以下结论：①∠CEG＝15°；②AF＝DF；③BH＝3AH BE＝HE+GE；正确的有_________．（填序号）三、解答题（5小题，每小题10分，共计50分）1、如图，矩形ABCD中，E、F是BC上的点，∠DAE=∠ADF．求证：BF=CE．2、如图，在△ABC中，点D是BC边的中点，点E是AD的中点，过A点作AF∥BC，且交CE的延长线于点F ，联结BF ．（1）求证：四边形AFBD 是平行四边形；（2）当AB=AC 时，求证：四边形AFBD 是矩形．3、如图，ABCD 的对角线AC 与BD 相交于点O ，过点B 作BP ∥AC ，过点C 作CP ∥BD ，BP 与CP 相交于点P ．（1）试判断四边形BPCO 的形状，并说明理由；（2）若将ABCD 改为矩形ABCD ，且6,8AB BC ==，其他条件不变，求四边形BPCO 的面积；（3）要得到矩形BPCO ，ABCD 应满足的条件是_________（填上一个即可）．4、如图，矩形OABC 在平面直角坐标系中，OB ，OC 是x 2﹣12x +32＝0的两根，OC >OA ，（1）求B 点的坐标．（2）把ABC 沿AC 对折，点B 落在点B '处，线段AB '与x 轴交于点D ，在平面上是否存在点P ，使D 、C 、B 、P 四点形成的四边形为平行四边形？若存在，请直接写出P 点坐标；若不存在，请说明理由．5、如图，四边形ABCD 中，AD BC ∥，90A D ∠=∠=︒，点E 是AD 的中点，连接BE ，将△ABE 沿BE 折叠后得到△GBE ，且点G 在四边形ABCD 内部，延长BG 交DC 于点F ，连接EF ．（1）求证：四边形ABCD 是矩形；（2）求证：GF DF =；（3）若点6AB =，8BC =，求DF 的长．-参考答案-一、单选题1、D【分析】根据多边形外角和定理求出正多边形的边数．【详解】∵正多边形的每一个外角都等于36°， ∴正多边形的边数＝36036＝10． 故选：D ．【点睛】本题考查了多边形内角与外角，根据外角和的大小与多边形的边数无关，由外角和求正多边形的边数，是常见的题目，需要熟练掌握．2、D【分析】利用矩形的性质，求证明90OAB ∠=︒，进而在Rt AOB ∆中利用勾股定理求出OB 的长度，弧长就是OB 的长度，利用数轴上的点表示，求出弧与数轴交点表示的实数即可．【详解】 解：四边形OABC 是矩形，∴90OAB ∠=︒， 在Rt AOB ∆中，由勾股定理可知：222OB OA AB =+，OB ∴==∴故选：D ．【点睛】本题主要是考查了矩形的性质、勾股定理解三角形以及数轴上的点的表示，熟练利用矩形性质，得到直角三角形，然后通过勾股定理求边长，是解决该类问题的关键．3、C【分析】由小明第一次回到出发点A，则小明走过的路程刚好是一个多边形的周长，由多边形的外角和为360︒，每次的转向的角度的大小刚好是多边形的一个外角，则先求解多边形的边数，从而可得答案. 【详解】解：由360=12,30可得：小明第一次回到出发点A，一个要走1210=120⨯米，故选C【点睛】本题考查的是多边形的外角和的应用，掌握“由多边形的外角和为360︒得到一共要走12个10米”是解本题的关键.4、A【分析】由题意先根据多边形的内角和公式先求出新多边形的边数，然后再根据截去一个角的情况进行讨论即可．【详解】解：设新多边形的边数为n，则（n-2）•180°=2340°，解得：n=15，①若截去一个角后边数增加1，则原多边形边数为14，②若截去一个角后边数不变，则原多边形边数为15，③若截去一个角后边数减少1，则原多边形边数为16，所以多边形的边数可以为14，15或16．故选：A．【点睛】本题考查多边形内角与外角，熟练掌握多边形的内角和公式（n-2）•180°（n为边数）是解题的关键．5、A【分析】利用直角三角形斜边的中线的性质可得答案．【详解】解：∵∠C=90°，若D为斜边AB上的中点，AB，∴CD=12∵AB的长为10，∴DC=5，故选：A．【点睛】此题主要考查了直角三角形斜边的中线，关键是掌握在直角三角形中，斜边上的中线等于斜边的一半．6、B【分析】根据平行四边形对角相等，即可求出C的度数．【详解】解：如图所示，∵四边形ABCD是平行四边形，∴A C ∠=∠，∴60A ∠=︒，∴60C ∠=°．故：B ．【点睛】本题考查了平行四边形的性质，解题的关键是掌握平行四边形的性质．7、C【分析】根据四边形内角和为360°及等边三角形的性质可直接进行求解．【详解】解：由题意得：等边三角形的三个内角都为60°，四边形内角和为360°，∴3606060240αβ∠+∠=︒-︒-︒=︒；故选C ．【点睛】本题主要考查多边形内角和及等边三角形的性质，熟练掌握多边形内角和及等边三角形的性质是解题的关键．8、D【分析】根据任何多边形的外角和都是360度，利用360除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．【详解】解：∵360°÷36°=10，∴这个多边形的边数是10．故选D ．【点睛】本题考查了多边形内角与外角，外角和的大小与多边形的边数无关，熟练掌握多边形内角与外角是解题关键．9、B【分析】先判断出四边形ACED 是平行四边形，从而得出DE 的长度，根据菱形的性质求出BD 的长度，利用勾股定理的逆定理可得出△BDE 是直角三角形，计算出面积即可．【详解】 解： 菱形ABCD ，6,AC =,3,2,5,,AD BC OA OC BD BO AB BC AD AC BD ∥在Rt △BCO 中，224,BOBC OC 即可得BD =8，,AC DE ∥ ∴四边形ACED 是平行四边形，∴AC =DE =6，5,CE AD∴ BE =BC +CE =10，222100,BE BD DE∴△BDE 是直角三角形，90,BDE ∠=︒∴S △BDE =12DE •BD =24．故选：B ．【点睛】本题考查了菱形的性质，勾股定理的逆定理及三角形的面积，平行四边形的判定与性质，求出BD 的长度，判断△BDE是直角三角形，是解答本题的关键．10、B【分析】首先可判断重叠部分为平行四边形，且两条丝带宽度相同；再由平行四边形的面积可得邻边相等，则重叠部分为菱形．【详解】解：过点A作AE⊥BC于E，AF⊥CD于F，因为两条彩带宽度相同，所以AB∥CD，AD∥BC，AE=AF．∴四边形ABCD是平行四边形．∵S▱ABCD=BC•AE=CD•AF．又AE=AF．∴BC=CD，∴四边形ABCD是菱形．故选：B【点睛】此题考查了菱形的判定，平行四边形的面积公式以及平行四边形的判定与性质，利用了数形结合的数学思想，其中菱形的判定方法有：一组邻边相等的平行四边形为菱形；对角线互相垂直的平行四边形为菱形；四条边相等的四边形为菱形，根据题意作出两条高AE和AF，熟练掌握菱形的判定方法是解本题的关键二、填空题1、10825或185或3【分析】过B作BM⊥AC于M，根据矩形的性质得出∠ABC＝90°，根据勾股定理求出AC，根据三角形的面积公式求出高BM，分为三种情况：①AB＝BP＝3，②AB＝AP＝3，③AP＝BP，分别画出图形，再求出面积即可．【详解】解：∵四边形ABCD是矩形，∴∠ABC＝90°，由勾股定理得：5AC，有三种情况：①当AB＝BP＝3时，如图1，过B作BM⊥AC于M，S△ABC＝1122AB BC AC BM⋅=⋅，1134=5 22BM∴⨯⨯⨯⨯，解得：125 MB=，∵AB＝BP＝3，BM⊥AC，∴95 AM PM===，∴AP＝AM+PM＝185，∴△PAB的面积＝111812108 225525 AP BM⋅=⨯⨯=；②当AB＝AP＝3时，如图2，∵BM＝125，∴△PAB的面积S＝11121832255 AP BM⋅=⨯⨯=；③作AB的垂直平分线NQ，交AB于N，交AC于P，如图3，则AP＝BP，BN＝AN＝13322=⨯，∵四边形ABCD是矩形，NQ⊥AC，∴PN∥BC，∵AN＝BN，∴AP＝CP，∴122PN BC==，∴△PAB的面积11323 22S AB NP=⋅=⨯⨯=;即△PAB 的面积为10825或185或3． 故答案为：10825或185或3． 【点睛】 本题主要是考查了矩形的性质、等腰三角形的判定以及勾股定理求边长，熟练掌握矩形的性质，利用等腰三角形的判定，分成三种情况讨论，是解决本题的关键．2、2【分析】先根据矩形的性质证明△ABC 是等边三角形，得到10cm AO AB ==，则20cm AC =，然后根据勾股定理求出BC ==，最后根据矩形面积公式求解即可．【详解】：如图所示，在矩形ABCD 中，∠AOB =60°，10cm AB =，∵四边形ABCD 是矩形，∴∠ABC =90°，1122OB OA AC BD ===， ∴△ABC 是等边三角形，∴10cm AO AB ==，∴20cm AC =，∴BC ==，∴2=ABCD S AB BC ⋅=，故答案为：2．【点睛】本题主要考查了矩形的性质，勾股定理，等边三角形的性质与判定，解题的关键在于能够熟练掌握矩形的性质．3、6【分析】根据题意把△ABE绕点A逆时针旋转90°到AD，交CD于点G，证明△AEF≌△AGF即可求得EF＝DF﹣BE＝7﹣1＝6．【详解】解：如图，把△ABE绕点A逆时针旋转90°到DA，交CD于点G，由旋转的性质可知，AG＝AE，DG＝BE，∠DAG＝∠BAE，∵∠EAF＝45°，∴∠DAG+∠BAF＝45°，又∵∠BAD＝90°，∴∠GAF＝45°，在△AEF 和△AGF 中，AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩， ∴△AEF ≌△AGF （SAS ）∴EF ＝GF ，∵BE ＝1，DF ＝7，∴EF ＝GF ＝DF ﹣DG ＝DF ﹣BE ＝7﹣1＝6.故答案为：6．【点睛】本题主要考查正方形的性质及全等三角形的判定和性质，构造全等三角形是解题的关键，注意旋转性质的应用．4、8【分析】正方形边长相等设为a ，对角线长已知，利用勾股定理求解边长的平方，即为正方形的面积．【详解】解：设边长为a ，对角线为4 24a =+28a ∴=故答案为：8．【点睛】本题考察了正方形的性质以及勾股定理．解题的关键在于求解正方形的边长．5、①【分析】由正方形的性质和等边三角形的性质可得CD CE =，30ECD ∠=︒，可得75CED ∠=︒，可求15CEG ∠=︒，故①正确；由“SAS “可证ABE DCE ∆≅∆，可得AE DE =，可证EH ED =，由线段垂直平分线的性质可得HF FD AF =>，故②错误；设2AB BC BE a ===，由等边三角形的性质和三角形中位线定理分别求出AH ，BH 的长，可判断③，通过证明点B ，点G ，点E ，点H 四点共圆，可得45BHG BEG ∠=∠=︒，可证HG =，由三角形三边关系可判断④，即可求解．【详解】 解：四边形ABCD 是正方形，AB BC CD AD ∴===，90DAB ADC ABC BCD ∠=∠=∠=∠=︒，BCE ∆是等边三角形，BE CE BC ∴==，60BCE EBC ∠=︒=∠，CD CE ∴=，30ECD ∠=︒，75CED ∴∠=︒，15CEG ∴∠=︒，故①正确；如图，连接AE ，过点E 作直线MN AD ⊥于N ，交BC 于M ，连接EH ，30ABE ABC EBC ∠=∠-∠=︒，ABE DCE ∴∠=∠，又AB CD =，BE CE =，()ABE DCE SAS ∴∆≅∆，AE DE∴=，∴∠=∠，EAD EDA∴∠=∠，EAH EHA∴=，AE EH∴=，EH ED又FG DH⊥，∴=，FH FD>，FH AF∴>，故②错误；FD AF设2===，AB BC BE aMN AD⊥，90∠=∠=∠=∠=︒，DAB ADC ABC BCD∴四边形ABMN是矩形，⊥，∴=，2AN BM==，MN BCMN AB a⊥，∆是等边三角形，MN BCEBC∴==，EM，BM MC a==，2∴=，AN DN aEN a又EH HD=，AH EN a∴==-，24BH AB AH a∴=-=-，2∴≠，故③错误；BH AH3如图，连接HG，∠=︒，60CEG15∠=︒，BEC∴∠=︒，BEG45∠+∠=︒，180ABC GEH∴点B，点G，点E，点H四点共圆，BHG BEG∴∠=∠=︒，45∴∠=∠=︒，BGH BHG45∴=，BH BG∴=，HG+>，EH EG HG∴+，故④错误；EH EG故答案为：①．【点睛】本题是四边形综合题，考查了全等三角形的判定和性质，等边三角形的性质，正方形的性质，勾股定理等知识，解题的关键是灵活运用这些性质解决问题．三、解答题1、见解析【分析】先证明=∠∠，然后证明△ABE≌△DCF，再根据全等三角形的性质得出结论．AEB DFC【详解】解：∵四边形ABCD 是矩形，∴AB CD =，90B C ∠=∠=︒，AD ∥BC ，∴∠ADF =∠CFD ，∠DAE =∠AEB ，∵=DAE ADF ∠∠，∴=AEB DFC ∠∠．在ABE △和DCF 中，=AEB DFC B CAB DC ∠∠⎧⎪∠=∠⎨⎪=⎩， ∴()ABE DCF AAS △≌△，∴BE CF =，∴BE -FE =CF -EF ，即BF =CE ．【点睛】本题主要考查了矩形的性质，全等三角形的性质与判定，熟知全等三角形的性质与判定条件是解题的关键．2、（1）见解析（2）见解析【分析】（1）首先证明△AEF ≌△DEC （AAS ），得出AF =DC ，进而利用AF ∥B D 、AF =BD 得出答案；（2）利用等腰三角形的性质，结合矩形的判定方法得出答案．【小题1】解：证明：（1）∵AF ∥BC ，∴∠AFC =∠FC D ．在△AFE 和△DCE 中，AEF DEC AFE DCE AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△AEF ≌△DEC （AAS ）．∴AF =DC ，∵BD =DC ，∴AF =BD ，∴四边形AFBD 是平行四边形；【小题2】∵AB =AC ，BD =DC ，∴AD ⊥B C ．∴∠ADB =90°．∵四边形AFBD 是平行四边形，∴四边形AFBD 是矩形．【点睛】此题主要考查了平行四边形的判定以及矩形的判定方法、全等三角形的判定与性质，正确掌握平行四边形的判定方法是解题关键．3、（1）平行四边形，理由见解析；（2）四边形BPCO的面积为24；（3）AB=BC或AC⊥BD等（答案不唯一）【分析】（1）利用平行四边形的判定：两组对边分别平行的四边形是平行四边形，即可证明．（2）利用矩形的性质，得到对角线互相平分，进而证明四边形BPCO是菱形，分别求出菱形的对角线长度，利用对角线乘积的一半，求解面积即可．（3）添加的条件只要可以证明AC BD即可得到矩形BPCO．【详解】解：（1）四边形BPCO是平行四边形，∵BP∥AC，CP∥BD，∴四边形BPCO是平行四边形．（2）连接OP．∵四边形ABCD是矩形，∴OB=12BD，OC=12AC，AC=BD，∠ABC=90°，∴OB=OC．又四边形BPCO是平行四边形，∴□BPCO是菱形．∴OP⊥BC.又∵AB⊥BC，∴OP∥AB.又∵AC∥BP，∴四边形ABPO是平行四边形，∴OP=AB=6.∴S菱形BPCO=118624 22BC OP⨯=⨯⨯=．（3）AB=BC或AC⊥BD等（答案不唯一）．当AB=BC时，ABCD为菱形，此时有：AC BD⊥，利用含有90︒的平行四边形为矩形，即可得到矩形BPCO，当AC⊥BD时，利用含有90︒的平行四边形为矩形，即可得到矩形BPCO．【点睛】本题主要是考查了平行四边形、矩形和菱形的判定和性质，熟练掌握特殊四边形的判定和性质，是求解该类问题的关键．4、（1）B（8，4）；（2）存在，P1（3，4），P2（13，4），P3（3，-4）【分析】（1）x2﹣12x+32＝0，解得x1=4，x2=8，OC>OA，故OA=4，OC=8，故B（8，4）．（2）由对折可知，∠DAC=∠BAC，故∠DAC=∠ACO，AD=CD，设AD=x，则OD=8-x，在Rt OAD中，满足222+=，解得x=5，故D点坐标为（3，0），由平行四边形性质可知P1（3，4），P2（13，OA OD AD4），P3（3，-4）时D、C、B、P四点形成的四边形为平行四边形．【详解】（1）x2﹣12x+32＝0，解得x1=4，x2=8，∵OC>OA，∴OA=4，OC=8，故B点坐标为（8，4）（2）由对折可知，∠DAC=∠BAC，又∵四边形OABC为矩形，∴AB//OC，∠BAC=∠ACO∴∠DAC=∠ACO，∴AD=CD，设AD=x，则OD=8-x，在Rt OAD中，满足222+=有OA OD AD2224(8)x x+-=化简得22+-+=166416x x x解得x=5，故OD=8-5=3故D点坐标为（3，0）由平行四边形性质可知P1（3，4），P2（13，4），P3（3，-4）时D、C、B、P四点形成的四边形为平行四边形．【点睛】本题考查了勾股定理，矩形的性质，平行四边形的性质，求出D点坐标，再根据平行四边形两对边分别平行且相等即可求得P点坐标．5、（1）证明见解析；（2）证明见解析；（3）83 DF【分析】（1）利用平行线的性质可得∠C=90°，再根据三个角是直角的四边形是矩形即可判定；（2）根据折叠的性质和中点的定义得出EG=ED，再用HL定理证明Rt△EGF≌Rt△EDF即可；（3）利用DF分别表示BF和FC，再在Rt△BCF中利用勾股定理求解即可．（1）证明：∵AD BC ∥，∴∠D +∠C =180°，∵90A D ∠=∠=︒，∴90C A D ∠=∠=∠=︒，∴四边形ABCD 为矩形；（2）证明：∵将△ABE 沿BE 折叠后得到△GBE ，∴△ABE ≌△GBE ，∴∠BGE =∠A ，AE =GE ，∵∠A =∠D =90°，∴∠EGF =∠D =90°，∵点E 是AD 的中点，∴EA =ED ，∴EG =ED ，在Rt △EGF 和Rt △EDF 中，EF EF EG ED=⎧⎨=⎩， ∴Rt △EGF ≌Rt △EDF （HL ）；∴GF DF =；（3）解：∵四边形ABCD 为矩形，△ABE ≌△GBE ，∴∠C =90°，BG =CD =AB =6，∵GF DF =；∴6BF BG GF DF =+=+，6CF DC DF DF =-=-，∴在Rt △BCF 中，根据勾股定理，222BF CF BC =+，即222(6)(6)8DF DF +=-+， 解得83DF =． 即83DF =．【点睛】本题考查矩形的性质和判定，全等三角形的判定定理，折叠的性质，勾股定理等．（1）掌握矩形的判定定理是解题关键；（2）能结合重点和折叠的性质得出EG =ED 是解题关键；（3）中能利用DF 正确表示Rt △BCF 中，BF 和CF 的长度是解题关键．。

专题1中点问题之构造三角形中位线类型一连接两点构造三角形的中位线1.△ABC 的中线BD ，CE 相交于O ，F ，G 分别是BO ，CO 的中点，求证:EF ∥DG ，且EF=DG。

2.已知:如图，在△ABC 中，点D 在AB 上，BD=AC ，E ，F ，G 分别是BC ，AD ，CD 的中点，EF ，CA 的延长线相交于点H 。

求证:(1)∠CGE=∠ACD+∠CAD ；(2)AH=AF。

类型二用角平分线十垂直构造三角形的中位线3.如图，△ABC 中，AD 平分∠BAC ，AD ⊥BD ，E 为BC 的中点.(1)求证:DE ∥AC;(2)若AB=4，AC=6，求DE 的长.4.(1)如图1，BD ，CE 分别是△ABC 的外角平分线，过点A 作AF ⊥BD ，AG ⊥CE ，垂足分别是F ，G ，连接FG.求证:()AC BC AB FG ++=21（提示:分别延长AF ，AG 与直线BC 相交）(2)如图2，若BD ，CE 分别是△ABC 的内角平分线，过点A 作AF ⊥BD ，AG ⊥CE ，垂足分别是F ，G ，连接FG.线段FG 与△ABC 的三边又有怎样的数量关系?写出你的猜想，并给予证明.类型三倍长法构造三角形的中位线5.如图，在△ABC 中，∠ABC=90°，AB=BC ，BD ⊥AC 于点D ，CE 平分∠ACB ，交AB 于点E ，交BD 于点F.求证:(1)△BEF 是等腰三角形;（2）()BF BC BD +=21类型四已知一边中点取另一边中点构造三角形的中位线6.如图，在△ABC 中，AD 是BC 边上的中线，点F 在AC 上，FC AF 21=，AD 与BF 交于点E.求证:点E 是AD 的中点.7.如图，在△ABC 中，D 为AC 上一点，AB=CD ，F 是AD 的中点，M 为BC 的中点，连接MF 并延长交BA 的延长线于点E ，G 为EF 的中点，求证:AG ⊥ME.专题2中点问题之构造斜边上的中线类型一利用直角三角形斜边上的中线求线段的长度1.已知，Rt △ABC 中，∠ACB=90°，AB=6cm ，D 为AB 中点，DE ⊥AC 于点E，∠A=30°，求BC ，CD 和AC 的长.类型二利用直角三角形斜边上的中线求角的度数2.如图，在Rt △ABC 中，∠BAC=90°，AD 是BC 边上的中线，ED ⊥BC 于点D ，交BA 延长线于点E ，若∠E=35°，求∠BDA 的度数.3.如图，在△ABC 中，∠ABC=90°，点D 是AC 中点，DE ⊥AC 于点D ，交BC 于点E，连接BD.求证:∠ABD=∠CED 。

沪科版八年级下册数学第19章四边形含答案一、单选题(共15题，共计45分)1、如图，将矩形纸片ABCD沿EF折叠（E，F分别是AD、BC上的点），使点B 与四边形CDEF内一点重合，若°，则等于（）A.110°B.115°C.120°D.130°2、平行四边形的一边长为6cm，则它的两条对角线长可以是（）A.4cm，6cmB.5cm，6cmC.4cm，8cmD.2cm，12cm3、如图，七边形ABCDEFG中，AB、ED的延长线交于点O，着∠1、∠2、∠3、∠4对应的邻补角和等于215°，则∠BOD的度数为（）A.30°B.35°C.40°D.45°4、如图，□ABCD中，AB=4，BC=5，AC的垂直平分线交AD于点E，则△CDE的周长是（）A.6B.8C.9D.105、如图，在ABCD中，对角线AC⊥AB，O为AC的中点，经过点O的直线交AD于E交BC于F，连结AF、CE，现在添加一个适当的条件，使四边形AFCE 是菱形，下列条件：①OE＝OA；②EF⊥AC；③E为AD中点，正确的有（）个。

A.0B.1C.2D.36、如果多边形的内角和是外角和的k倍，那么这个多边形的边数是（）．A.kB.2k＋1C.2k＋2D.2k－27、我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.已知四边形ABCD的中点四边形是正方形，对角线AC与BD的关系，下列说法正确的是（）A.AC，BD相等且互相平分B.AC，BD垂直且互相平分C.AC，BD相等且互相垂直D.AC，BD垂直且平分对角8、顺次连结四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是 ( )A.AB∥DCB.AC=BDC.AC⊥BDD.AB=DC9、给出下列判断：①一组对边平行，另一组对边相等的四边形是平行四边形；②对角线相等的四边形是矩形；③对角线互相垂直且相等的四边形是正方形；④有一条对角线平分一个内角的平行四边形为菱形．其中，不正确的有（）A.1个B.2个C.3个D.4个10、如图，已知Rt△ABC中，AC=b，BC=a，D1是斜边AB的中点，过D1作D 1E1⊥AC于E1，连结BE1交CD1于D2；过D2作D2E2⊥AC于E2，连结BE2交CD1于D3；过D3作D3E3⊥AC于E3，…，如此继续，可以依次得到点D4，D 5，…，Dn，分别记△BD1E1，△BD2E2，△BD3E3，…，△BDnEn的面积为S1， S2， S3，…Sn．则Sn为（）A. B. C. D.11、如图，菱形ABCD中，∠B＝60°，AB＝4，则以AC为边的正方形ACEF的周长为( )A.14B.15C.16D.1712、如图，正方形ABCD的边长为4，分别以正方形的三边为直径在正方形内部作半圆，则阴影部分的面积之和是（）A.8B.4C.16πD.4π13、如图，在□ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则△DEF与四边形EFCO的面积比为（）A.1: 4B.1:5C.1:6D.1: 714、如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为，点A，B，E在x轴上，若正方形BEFG的边长为6，则点C的坐标为（）A.（2，2）B.（3，1）C.（3，2）D.（4，2）15、▱ABCD的周长为40 cm，△ABC的周长为25 cm，则对角线AC长为（）A.5cmB.15cmC.6cmD. 16cm二、填空题(共10题，共计30分)16、如图，折叠形ABCD的一边AD，点D落在BC边上的点F处，AE是折痕，已知AB=8cm，BC=10cm．则CE=________cm．17、如图，在平行四边形ABCD中，延长AD到点E，使DE=AD，连接EB，EC，DB请你添加一个条件________，使四边形DBCE是矩形．18、已知一个平行四边形的一组邻边长分别是方程(x-5)²=x-5的两根，则该平行四边形的周长为________。

沪科版八年级数学下册第19章四边形一、单选题1．正五边形的每个外角等于( )A．36°B．60°C．72°D．108°2．如图，DE是△ABC的中位线，若BC＝8，则DE的长为()A．2 B．4 C．6 D．83．如图所示，在□ABCD中，对角线AC、BD相交于点O，且AB≠AD，则下列式子不正确的是（）A．AC⊥BD B．AB＝CD C．BO＝OD D．∠BAD＝∠BCD 4．下列关于矩形的说法，正确的是（）．A．对角线相等的四边形是矩形B．对角线互相平分的四边形是矩形C．矩形的对角线互相垂直且平分D．矩形的对角线相等且互相平分5．矩形ABCD的对角线AC、BD相交于点O，∠AOD＝120°，AC＝8，则△ABO的周长为（）A．12 B．16 C．20 D．246．如图，顺次连接四边形ABCD各边的中点得到四边形EFGH，要使四边形EFGH为菱形，应添加的条件是()A．AB∥DC B．AB＝DCC．AC⊥BD D．AC＝BD7．如图，在△ABC中，AC＝BC，D，E分别是边AB，AC的中点，延长DE到点F，使EF ＝DE，连接AF，CF，则四边形ADCF一定是()A．矩形B．菱形C．正方形D．不能确定8．如图，将长为8 cm，宽为4 cm的矩形纸片ABCD折叠，使点A与点C重合，则折痕EF 的长为()A B．2C．3 D．4二、填空题9．如图，在平行四边形ABCD中，添加一个条件_____使平行四边形ABCD是菱形．10．如图，菱形ABCD的周长为8 cm，∠BAD＝60°，则AC＝________cm.11．如图，已知正方形ABCD的边长为a，连接AC，BD，CE平分∠ACD交BD于点E，则DE的长为____________．12．如图．四边形ABCD是矩形，点E在线段CB的延长线上，连接DE交AB于点F，∠AED=2∠CED，点G是DF的中点，若BE=1，AG=4，则AB的长为三、解答题13．如图，四边形风筝的四个内角∠A，∠B，∠C，∠D的度数之比为1.1∶1∶0.5∶1.求它的四个内角的度数．14．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE，已知∠BAC=30°，EF⊥AB，垂足为F，连接DF（1）试说明AC=EF；（2）求证：四边形ADFE是平行四边形．15．如图，在正方形ABCD的对角线AC上取一点E，使CE＝CD，过点E作EF⊥AC交AD于点F.求证：AE＝EF＝DF.16．如图，在▱ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE=DF．（1）求证：▱ABCD是菱形；（2）若AB=5，AC=6，求▱ABCD的面积．参考答案1．C【解析】试题分析：五边形的外角和为360°，则每个外角的度数为360°÷5=72°. 考点：多边形的外角2．B【解析】【分析】已知DE 是ABC 的中位线，8BC =，根据中位线定理即可求得DE 的长．【详解】解：DE 是ABC 的中位线，8BC =，142DE BC ∴==， 故选B ．【点睛】此题主要考查三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．3．A【解析】试题分析：因为在ABCD 中， AB≠AD ，所以ABCD 不是菱形，所以AC ⊥BD 错误，故选A.考点：平行四边形的性质.4．D【解析】分析：根据定义有一个角是直角的平行四边形叫做矩形．矩形的性质：1．矩形的四个角都是直角2．矩形的对角线相等3．矩形所在平面内任一点到其两对角线端点的距离的平方和相等4．矩形既是轴对称图形，也是中心对称图形（对称轴是任何一组对边中点的连线）．5．对边平行且相等6．对角线互相平分，对各个选项进行分析即可．解答：解：A、因为对角线相等的平行四边形是矩形，所以本选项错误；B、因为对角线互相平分且相等的四边形是矩形，所以本选项错误；C、因为矩形的对角线相等且互相平分，所以本选项错误；D、因为矩形的对角线相等且互相平分，所以本选项正确．故选D．5．A【解析】【分析】根据矩形性质求出AO=BO=4，得出等边三角形AOB，求出AB，即可求出答案．【详解】解：∵四边形ABCD是矩形，AC=8，∴AC=BD，AC=2AO，BD=2BO，∴AO=BO=4，∵∠AOD=120°，∴∠AOB=60°，∴△AOB是等边三角形，∴AB=AO=4，∴△ABO的周长是4+4+4=12，故选A．【点睛】本题考查了矩形性质，等边三角形的性质和判定的应用，注意：矩形的对角线相等且互相平分．6．D 【解析】【分析】连AC，BD，根据三角形中位线的性质得到EF∥AC，EF=12AC；HG∥AC，HG=12AC，即有四边形EFGH为平行四边形，当AB∥DC和AB=DC，只能判断四边形EFGH为平行四边形；当AC⊥BD，只能判断四边形EFGH为矩形；当AC=BD，可判断四边形EFGH为菱形．【详解】解：连AC，BD，如图，∵E、F、G、H为四边形ABCD各中点，∴EF∥AC，EF=12AC；HG∥AC，HG=12AC，∴四边形EFGH为平行四边形，要使四边形EFGH为菱形，则EF=EH，而EH=12 AC，∴AC=BD．当AB∥DC和AB=DC，只能判断四边形EFGH为平行四边形，故A、B选项错误；当AC⊥BD，只能判断四边形EFGH为矩形，故C选项错误；当AC=BD，可判断四边形EFGH为菱形，故D选项正确．故选D．【点睛】本题考查了菱形的判定定理：邻边相等的平行四边形是菱形．也考查了平行四边形的判定以及三角形中位线的性质．7．A【解析】【分析】先证明四边形ADCF是平行四边形，再证明AC=DF即可．【详解】解：∵E是AC中点，∴AE=EC，∵DE=EF，∴四边形ADCF是平行四边形，∵AD=DB，AE=EC，∴DE=12 BC，∴DF=BC，∵CA=CB，∴AC=DF，∴四边形ADCF是矩形；故选：A．【点睛】本题考查了矩形的判定、等腰三角形的性质、平行四边形的判定、三角形中位线定理；熟记对角线相等的平行四边形是矩形是解决问题的关键．8．B【解析】【分析】连接A、C，则EF垂直平分AC，推出△OEC∽△BCA，根据勾股定理，可以求出AC的长度，根据相似比求出OE，即可得出EF的长．【详解】解：连接AC，与EF交于O点，∵E点在AB上，F在CD上，A、C点重合，EF是折痕，∴AO=CO，EF⊥AC，∵AB=8，BC=4，∴∵AE=CE，∴∠EAO=∠ECO，∴△OEC∽△BCA，∴OE：BC=OC：BA，∴∴故答案为【点睛】本题主要考查了矩形的性质、勾股定理、相似三角形的判定和性质、折叠的性质；熟练掌握矩形的性质和折叠的性质，证明三角形相似是解决问题的关键．9．AB=BC(或AC⊥BD)答案不唯一【解析】【分析】根据邻边相等的平行四边形是菱形可知添加条件AB=BC．【详解】解：添加条件：AB=BC，根据邻边相等的平行四边形是菱形可以判定四边形ABCD是菱形．故答案为AB=BC．【点睛】此题主要考查了菱形的判定，关键是熟练掌握菱形的判定方法：①菱形定义：一组邻边相等的平行四边形是菱形；②四条边都相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形．10．.【解析】试题分析：∵菱形ABCD周长为8cm．∠BAD=60°∴△AOB为直角三角形，AB=2cm，∠OAB=30°，OA=OC，∴，∴．考点：1.菱形的性质；2.解直角三角形．11．－1)a【解析】【分析】过E 作EF ⊥DC 于F ，根据正方形的性质，和角平分线的性质，以及勾股定理即可求出DE 的长．【详解】解：过E 作EF ⊥DC 于F ，∵四边形ABCD 是正方形，∴AC ⊥BD ，∵CE 平分∠ACD 交BD 于点E ，∴EO=EF ，∵正方形ABCD 的边长为a ，∴a ，∴CO=12AC=2a ，∴CF=CO=2a ，∴EF=DF=DC-CF=a-2a ，∴－1)a故答案为－1)a【点睛】 本题考查了正方形的性质：对角线相等，互相垂直平分，并且每条对角线平分一组对角、角平分线的性质：角的平分线上的点到角的两边的距离相等以及勾股定理的运用，熟练掌握正方形的性质是本题的关键．12【解析】∵四边形ABCD是矩形，∴AD∥BC．∴∠CED=∠ADE．∵四边形ABCD是矩形，∴∠BAD=900．∵点G是DF的中点，∴AG=12DF=DG．∴∠CGE=2∠ADE=2∠CED．又∵∠AED=2∠CED，∴∠CGE=∠AED．∴AE=AG．又∵BE=1，AG=4，∴AE=4．∴AB===13．∠A，∠B，∠C，∠D的度数分别为110°，100°，50°，100°.【解析】【分析】设一份是x，用同一个未知数表示出各个角，根据四边形的内角和定理列方程求解．【详解】解：设四边形的四个内角∠A，∠B，∠C，∠D的度数分别为1.1x，x，0.5x，x，则1.1x＋x＋0.5x＋x＝360°，解得x＝100°.则1.1x＝110°，0.5x＝50°.故∠A，∠B，∠C，∠D的度数分别为110°，100°，50°，100°.【点睛】本题考查了四边形的内角和定理，多边形内角和定理：（n-2）•180 （n≥3）且n为整数）．14．证明见解析．【解析】【分析】（1）一方面Rt△ABC中，由∠BAC=30°可以得到AB=2BC，另一方面△ABE是等边三角形，EF⊥AB，由此得到AE=2AF，并且AB=2AF，从而可证明△AFE≌△BCA，再根据全等三角形的性质即可证明AC=EF．（2）根据（1）知道EF=AC，而△ACD是等边三角形，所以EF=AC=AD，并且AD⊥AB，而EF⊥AB，由此得到EF∥AD，再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形．【详解】证明：（1）∵Rt△ABC中，∠BAC=30°，∴AB=2BC．又∵△ABE是等边三角形，EF⊥AB，∴AB=2AF．∴AF=BC．∵在Rt△AFE和Rt△BCA中，AF=BC，AE=BA，∴△AFE≌△BCA（HL）．∴AC=EF．（2）∵△ACD是等边三角形，∴∠DAC=60°，AC=AD．∴∠DAB=∠DAC+∠BAC=90°．∴EF∥AD．∵AC=EF，AC=AD，∴EF=AD．∴四边形ADFE是平行四边形．考点：1．全等三角形的判定与性质；2．等边三角形的性质；3．平行四边形的判定．15．详见解析.【解析】【分析】连接CF，求证△CEF≌△CDF，可以求证EF=DF．进一步求证△AEF为等腰直角三角形，得出EF=AE，即可证得结论．【详解】证明：如图，连接CF，在正方形ABCD中，∠D＝∠DAB＝90°，AC平分∠DAB，∴∠DAC＝∠CAB＝45°.又∵EF⊥AC，∴∠DAC＝∠AFE＝45°，∴AE＝EF.在Rt△CEF和Rt△CDF中，CE CD CF CF=⎧⎨=⎩∴Rt△CEF≌Rt△CDF(HL)，∴EF＝DF，∴AE＝EF＝DF.【点睛】本题考查了正方形的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质，连接CF，并且求证Rt△CEF≌Rt△CDF是解本题的关键．16．（1）证明见解析；（2）S平行四边形ABCD =24【解析】【分析】（1）利用全等三角形的性质证明AB=AD即可解决问题；（2）连接BD交AC于O，利用勾股定理求出对角线的长即可解决问题；【详解】（1）∵四边形ABCD是平行四边形，∴∠B=∠D，∵AE⊥BC，AF⊥CD，∴∠AEB=∠AFD=90°，∵BE=DF，∴△AEB≌△AFD，∴AB=AD，∴四边形ABCD是平行四边形；（2）连接BD交AC于O，∵四边形ABCD是菱形，AC=6，∴AC⊥BD，AO=OC=12AC=12×6=3，∵AB=5，AO=3，∴，∴BD=2BO=8，∴S平行四边形ABCD =12×AC×BD=24．【点睛】本题考查了菱形的判定和性质、勾股定理、全等三角形的判定和性质等知识，熟练掌握相关的性质与定理、正确添加辅助线是解题的关键.。