分段线性插值

插值法——线性分段插值 1.插值函数%%分段线性插值function PLI = Piecewise_linear_interpolation(X,f,precision)[m,n] = size(X);a = min(X);b = max(X);X = sort(X);F = subs(f,X);for k = 1:n-1B = Basic_fun(X,k);I = B(1)*F(k)+B(2)*F(k+1);PLI{1,k} = [X(k),X(k+1)];PLI{2,k} = I;t{k} = X(k):(X(k+1)-X(k))/precision:X(k+1);T{k} = subs(I,t{k});Y_real{k} = subs(f,t{k});endfor k = 1:n-1t_((precision+1)*(k-1)+1:(precision+1)*k) = t{k};T_((precision+1)*(k-1)+1:(precision+1)*k) = T{k};Y_real_((precision+1)*(k-1)+1:(precision+1)*k)= Y_real{k};endh = figure;set(h,'color','w');plot(X,F,'r*',t_,T_,'g',t_,Y_real_,'b');xlabel('x shaft');ylabel('y shaft');legend('F：节点对应函数值','T：分段线性插值函数图像','Y_real：真实函数图像');title('分段线性插值');grid onend 2.基函数%%基函数，max(X)>k>0function BF = Basic_fun(X,k)X = sort(X);syms x;BF(1) = (x-X(k+1))/(X(k)-X(k+1));BF(2) = (x-X(k))/(X(k+1)-X(k));end 3.拟合值函数%%线性插值拟合值function LIV = Linear_interpolation_value(X,f,precision,x_value)[m,n] = size(X);a = min(X);b = max(X);X = sort(X);Answer = Piecewise_linear_interpolation(X,f,precision);for i = 1:n-1if x_value >= X(i) && x_value <= X(i+1)s = i;endendLIV{1,1} = '线性插值拟合值';LIV{2,1} = vpa(subs(Answer{2,s},x_value),6);LIV{1,2} = '真实值';LIV{2,2} = vpa(subs(f,x_value),6);LIV{1,3} = '误差';LIV{2,3} = abs(LIV{2,1}-LIV{2,2});end 4.例⼦clear allclcX = -5:1:5;syms x;f = - 0.08858*x^8 + 3.694*x^7 - 64.7*x^6 + 617.8*x^5 - 3490.0*x^4 + 11820.0*x^3 - 23150.0*x^2 + 23580.0*x - 9319.0; precision = 200;%%分段线性插值disp('分段线性插值');Piecewise_linear_interpolation(X,f,precision) 结果分段线性插值S =2×10 cell 数组列 1 ⾄ 4{1×2 double} {1×2 double} {1×2 double} {1×2 double} {1×1 sym } {1×1 sym } {1×1 sym } {1×1 sym }列 5 ⾄ 8{1×2 double} {1×2 double} {1×2 double} {1×2 double} {1×1 sym } {1×1 sym } {1×1 sym } {1×1 sym }列 9 ⾄ 10{1×2 double} {1×2 double}{1×1 sym } {1×1 sym }>> S{2,:}ans =(227077586881*x)/50000 + 37695704689/2500ans =(3983468847*x)/2000 + 60987657739/12500ans =(7723057429*x)/10000 + 30518164433/25000ans =(2518396259*x)/10000 + 4494858583/25000ans =(3136314129*x)/50000 - 9319ans =(465835271*x)/50000 - 9319ans =(422501*x)/10000 - 1113617/25000ans =4111433/25000 - (622509*x)/10000ans =- (271*x)/80 - 151661/12500ans =2072089/2500 - (10681481*x)/50000 图像如下。

分段线性插值分段线性插值是一种在机器学习、数学、信号处理等领域中广泛应用的方法。

分段线性插值的主要目的是为漏洞、持续时间等数据展示提供更好的视觉效果，同时也可以使数据更容易进行处理。

在分段线性插值中，每一段数据都可以看作是一条直线段。

通过在相邻数据点之间插入一条直线来实现插值。

每个数据点或任意数段可以称为一个插值区间，插值区间内部的数据点都采用一条直线进行插值，直线的斜率由插值区间上下数据点构成。

例如：在一个区间（x1,y1）和（x2,y2）之间进行插值，其中x1<x<x2。

那么，我们可以使用线性公式y = mx + b来估计数据点的y值。

方程中m是插值区间的斜率，通过公式m = (y2-y1)/(x2-x1)计算。

而b是在插值区间x1和x2之间的截距，通过公式b = y1 - m x1计算。

最后，我们就可以通过已知的数据点，估计同一段中任意点的y值。

下面我们通过一个实例来进一步解释分段线性插值的应用。

比如我们有一组工作时间数据如下:|年份| 工作时间 ||----|----|| 2010 | 6.5 || 2011 | 7.0 || 2013 | 7.5 || 2015 | 8.0 |目前，我们需要在2012年估计工作时间。

首先，我们需要找到分段线性插值的区间。

2012年的数据点在2011年和2013年之间。

因此，我们可以使用2011年和2013年之间的数据点进行插值。

然后，通过计算斜率来确定m和b的值。

斜率可以通过公式m = (y2-y1)/(x2-x1)来计算。

2011年和2013年的工作时间分别是7.0和7.5，年份分别是2011和2013。

因此，斜率为：（7.5-7.0）/（2013年-2011年）= 0.25/2 = 0.125插值区间的y截距b可以通过公式b = y1 - m x1来计算。

这使得我们可以计算出截距：接下来，我们就可以使用斜率和截距来计算2012年的工作时间，这将是我们所需的数据点的估计值：y = mx + b= 0.125 * 2012 + 258.375= 259.875。

计算方法分段线性_三次样条插值分段线性和三次样条插值是两种常用的插值方法，在数值分析和插值问题中广泛使用。

1.分段线性插值分段线性插值是一种简单直观的插值方法，将插值区间划分为若干个子区间，在每个子区间上用线性函数进行插值。

假设给定的插值节点有n+1 个，节点为 (x0, y0), (x1, y1), ..., (xn, yn)，并且满足 x0 <x1 < ... < xn。

则对于任意 xx 使得 x 在 [xi, xi+1] 之间，可以通过线性插值得到其函数值 yy，即：yy = yi + (xx - xi) * (yi+1 - yi) / (xi+1 - xi)分段线性插值方法简单易懂，适用于一些较简单的插值问题。

但是由于插值函数在节点之间是线性的，可能不能准确地反映出数据的特征，因此不适用于一些需要高精度的插值问题。

三次样条插值是一种更复杂、更精确的插值方法，将插值区间划分为若干个子区间，在每个子区间上用三次多项式进行插值。

三次样条插值方法的基本思想是找到一组三次多项式，满足在每个子区间内插值点的函数值和一阶导数值相等，并且两个相邻多项式在节点处的二阶导数值也相等。

具体的求解步骤如下：(1) 假设有 n+1 个插值节点 (x0, y0), (x1, y1), ..., (xn, yn)，构造 n 个三次多项式，即每个多项式在 [xi, xi+1] 之间插值。

(2) 对每个子区间内的多项式进行插值，设第 i 个子区间的多项式为 Si(x) = ai + bi(x-xi) + ci(x-xi)^2 + di(x-xi)^3、将插值节点的函数值和一阶导数值代入多项式中，可以得到 n 个线性方程，利用这 n 个线性方程可以求解出 n 个子区间的系数。

(3)由于n个子区间的多项式必须在节点处一阶导数值相等，因此再设立n-1个方程，利用这些方程可以求解出n-1个子区间的二阶导数值。

(4)将求解得到的系数和二阶导数值代入每个子区间的多项式中，得到完整的三次样条插值函数。

《数值分析》实验报告实验序号：实验五实验名称：分段线性插值法1、实验目的：随着插值节点的增加，插值多项式的插值多项式的次数也增加，而对于高次的插值容易带来剧烈的震荡，带来数值的不稳定（Runge现象）。

为了既要增加插值的节点，减小插值的区间，以便更好的逼近插值函数，又要不增加插值多项式的次数以减少误差，可采用分段线性插值。

2、实验内容：求一个函数（X）用来近似函数f（x），用分段线性插值的方法来求解近似函数（X）并画出近似函数图像及原函数图像。

设在区间［a,b］上，给定n+1个插值节点a x0 X j x2 ... x n b和相应的函数值y。

，y i,…，y n，求一个插值函数（x），满足以下条件：（1）（X j） y j（ j 0,1,2,…,n）；（2）（x）在每一个小区间［X j,X ji］上是线性函数。

1对于给定函数f（x）2,-1 X 1。

在区间-1,1上画出f（x）和分段线性插1 25x值函数（x）的函数图像。

1.分段线性插值的算法思想：分段线性插值需要在每个插值节点上构造分段线性插值基函数丨j（X），然后再作它们的线性组合。

分段线性插值基函数的特点是在对应的插值节点上函数值取1,其它节点上函数值取0。

插值基函数如下：X X n 1 ——,X n 1 X X nI n (X ) X n X n 10, 其它 设在节点a w X 0<X 1<…W b=f(xi),(i=0,1,2,…,n)求折线函数 L (X )满足： (1)L(X ) € C[a,b] (2)L(x[i]=y[i]) (3) L(X )在每个小区间(x[i],x[i+1] )上是线性插值函数C( x )叫做区间[a,b]上对数据(x[j],y[j]) (j=0,1,2,…,n)的分段区间函数。

利用一介拉格朗日函数，直接得到线性插值函数为：L(X 0)= ( X -X [1] ) /x[0]-x[1];(x[0] w X w X [1])L(X 0)=0(X [1] w x w X [n])分段线性方程的表达式：0( X ) =E (j=0,..,n)y[j]*L[j](x);3、实验代码：// LDIg.cpp : implementation file//#include "stdafx.h"#i nclude "L.h"#i nclude "LDlg.h"#ifdef _DEBUG#defi ne new DEBUG_NEW#un def THIS_FILEstatic char THIS_FILE[] = __FILE.#en difx X j 1,X j 1 X X jX j X j 1X X-,X g X X i l o (X ) X o X i0, 其它I j (X ) 亠X j X j X j 1X X j 1 0, 其它/////////////////////////////////////////////////////////////////////////////// CAboutDlg dialog used for App Aboutclass CAboutDlg : public CDialog{public:CAboutDlg();// Dialog Data//{{AFX_DATA(CAboutDlg)enum { IDD = IDD_ABOUTBOX };//}}AFX_DATA// ClassWizard generated virtual function overrides//{{AFX_VIRTUAL(CAboutDlg)protected:virtual void DoDataExchange(CDataExchange* pDX);// DDX/DDV support //}}AFX_VIRTUAL// Implementationprotected://{{AFX_MSG(CAboutDlg)//}}AFX_MSGDECLARE_MESSAGE_MAP()};CAboutDlg::CAboutDlg() : CDialog(CAboutDlg::IDD)//{{AFX_DATA_INIT(CAboutDlg)}//}}AFX_DATA_INITvoid CAboutDlg::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CAboutDlg)//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CAboutDlg, CDialog)//{{AFX_MSG_MAP(CAboutDlg)// No message handlers//}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CLDlg dialogCLDlg::CLDlg(CWnd* pParent /*=NULL*/): CDialog(CLDlg::IDD, pParent){//{{AFX_DATA_INIT(CLDlg)// NOTE: the ClassWizard will add member initialization here//}}AFX_DATA_INIT// Note that LoadIcon does not require a subsequent DestroyIcon in Win32 m_hIcon = AfxGetApp()->LoadIcon(IDR_MAINFRAME);void CLDlg::DoDataExchange(CDataExchange* pDX)CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CLDlg)// NOTE: the ClassWizard will add DDX and DDV calls here //}}AFX_DATA_MAP }BEGIN_MESSAGE_MAP(CLDlg, CDialog)//{{AFX_MSG_MAP(CLDlg)ON_WM_SYSCOMMAND()ON_WM_PAINT()ON_WM_QUERYDRAGICON()ON_BN_CLICKED(IDC_LARGRI, OnLargri)ON_BN_CLICKED(IDC_BUTTON2, OnButton2)ON_BN_CLICKED(IDC_HERMITE, OnHermite) //}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CLDlg message handlersBOOL CLDlg::OnInitDialog(){CDialog::OnInitDialog();// Add "About..." menu item to system menu.// IDM_ABOUTBOX must be in the system command range.ASSERT((IDM_ABOUTBOX & 0xFFF0) == IDM_ABOUTBOX);ASSERT(IDM_ABOUTBOX < 0xF000);CMenu* pSysMenu = GetSystemMenu(FALSE);if (pSysMenu != NULL){CString strAboutMenu;strAboutMenu.LoadString(IDS_ABOUTBOX);if (!strAboutMenu.IsEmpty()){pSysMenu->AppendMenu(MF_SEPARATOR);pSysMenu->AppendMenu(MF_STRING, IDM_ABOUTBOX, strAboutMenu);}}// Set the icon for this dialog. The framework does this automatically // when the application's main window is not a dialog SetIcon(m_hIcon, TRUE); // Set big iconSetIcon(m_hIcon, FALSE); // Set small icon// TODO: Add extra initialization herereturn TRUE; // return TRUE unless you set the focus to a control}void CLDlg::OnSysCommand(UINT nID, LPARAM lParam){if ((nID & 0xFFF0) == IDM_ABOUTBOX){CAboutDlg dlgAbout;dlgAbout.DoModal();}else{CDialog::OnSysCommand(nID, lParam);}}// If you add a minimize button to your dialog, you will need the code below// to draw the icon. For MFC applications using the document/view model,// this is automatically done for you by the framework.void CLDlg::OnPaint(){if (IsIconic()){CPaintDC dc(this); // device context for paintingSendMessage(WM_ICONERASEBKGND, (WPARAM) dc.GetSafeHdc(), 0);// Center icon in client rectangleint cxIcon = GetSystemMetrics(SM_CXICON);int cyIcon = GetSystemMetrics(SM_CYICON);CRect rect;GetClientRect(&rect);int x = (rect.Width() - cxIcon + 1) / 2;int y = (rect.Height() - cyIcon + 1) / 2;// Draw the icondc.DrawIcon(x, y, m_hIcon);else}CDialog::OnPaint();}}// The system calls this to obtain the cursor to display while the user drags // the minimized window.HCURSOR CLDlg::OnQueryDragIcon(){return (HCURSOR) m_hIcon;}void CLDlg::OnOK(){int x00=300,y00=350,i,j;double x;CDC *pDC=GetDC(); pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);// 画坐标轴与原函数for(i=-700; i<=700; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));for(x=-1; x<=1; x+=0.001)}double j=400.0/(1+25*x*x);pDC->SetPixel(x*500,j,RGB(255,0,0));}pDC->TextOut(-30,-10,"0");pDC->TextOut(-30,430,"1");pDC->TextOut(490,-10,"1");pDC->TextOut(-490,-10,"-1");pDC->MoveTo(-10,680); //x箭头pDC->LineTo(0,700);pDC->MoveTo(0,700);pDC->LineTo(10,680);pDC->MoveTo(680,10); //y 箭头pDC->LineTo(700,0);pDC->MoveTo(700,0);pDC->LineTo(680,-10);pDC->TextOut(-30,700,"y");pDC->TextOut(700,-10,"x");}void CLDlg::OnLargri(){int x00=300,y00=350,i,j;double x;CDC *pDC=GetDC();pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);// 画坐标轴for(i=-700; i<=700; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));}double yx[]={-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1};pDC->TextOut(-30,-10,"0");pDC->TextOut(-30,430,"1");pDC->TextOut(490,-10,"1");pDC->TextOut(-490,-10,"-1");pDC->MoveTo(-10,680); //x 箭头pDC->LineTo(0,700);pDC->MoveTo(0,700);pDC->LineTo(10,680);pDC->MoveTo(680,10); //y 箭头pDC->LineTo(700,0);pDC->MoveTo(700,0);pDC->LineTo(680,-10);pDC->TextOut(-30,700,"y");pDC->TextOut(700,-10,"x");// 拉格朗日差值的函数double yy[12],lx[12],ly[12];double l_fenzi[12],l_fenmu[12];double l_x,l_y;for(i=0; i<=10; i++){yy[i]=1.0/(1+25*yx[i]*yx[i]);}for(i=0; i<=10; i++){l_fenmu[i]=1.0;for(j=0; j<=10; j++){if(i!=j)l_fenmu[i]=l_fenmu[i]*(yx[i]-yx[j]);}}double qq,pp;for(qq=-1; qq<=1; qq+=0.0003){for(i=0; i<=10; i++){l_fenzi[i]=1.0;for(j=0; j<=10; j++){if(i!=j)l_fenzi[i]=l_fenzi[i]*(qq-yx[j]);}}pp=0;for(i=0; i<=11; i++){pp=pp+1.0/(1+25*yx[i]*yx[i])*l_fenzi[i]/l_fenmu[i];pDC->SetPixel(qq*500,pp*390+5,RGB(132,112,225));}}void CLDlg::OnButton2(){int x00=300,y00=350,i,j;double x;CDC *pDC=GetDC();pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);// 画坐标轴与原函数for(i=-700; i<=700; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));}double yx[]={-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1};double yy[14];for(i=0; i<=10; i++){yy[i]=1.0/(1+25*yx[i]*yx[i]);}pDC->TextOut(-30,-10,"0");pDC->TextOut(-30,430,"1"); pDC->TextOut(490,-10,"1"); pDC->TextOut(-490,-10,"-1");pDC->MoveTo(-10,680); //xpDC->LineTo(0,700);pDC->MoveTo(0,700);pDC->LineTo(10,680);pDC->MoveTo(680,10); //y 箭头pDC->LineTo(700,0);pDC->MoveTo(700,0);pDC->LineTo(680,-10);pDC->TextOut(-30,700,"y");pDC->TextOut(700,-10,"x");// 线性分段差值的图像CPen pen;CPen*oldpen;pen.CreatePen(PS_SOLID,5,RGB(0,0,0));oldpen=pDC->SelectObject(&pen);for(i=0; i<10; i++){pDC->MoveTo(yx[i]*480,yy[i]*400);pDC->LineTo(yx[i+1]*480,yy[i+1]*400);}void CLDlg::OnHermite()箭头}int x00=300,y00=350,i,j;double x;CDC *pDC=GetDC();pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);// 画坐标轴与原函数for(i=-700; i<=700; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));}double yx[]={-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1};double yy[12];for(i=0; i<=10; i++){yy[i]=1.0/(1+25*yx[i]*yx[i]);}pDC->TextOut(-30,-10,"0");pDC->TextOut(-30,430,"1");pDC->TextOut(490,-10,"1");pDC->TextOut(-490,-10,"-1");pDC->MoveTo(-10,680); //x 箭头pDC->LineTo(0,700);pDC->MoveTo(0,700);pDC->LineTo(10,680);pDC->MoveTo(680,10); //y 箭头pDC->LineTo(700,0);pDC->MoveTo(700,0);pDC->LineTo(680,-10);pDC->TextOut(-30,700,"y");pDC->TextOut(700,-10,"x");// 分段三次Hermite 差值的函数double x0,x1,yd1,yd0,y1,y0;for(i=0; i<10; i++){x0=yx[i],x1=yx[i+1];y0=1.0/(1+25*x0*x0);y1=1.0/(1+25*x1*x1);yd0=-(50*x0)*1.0/((1+25*x0*x0)*(1+25*x0*x0));yd1=-(50*x1)*1.0/((1+25*x1*x1)*(1+25*x1*x1));for(double qq=x0; qq<x1; qq+=0.005){double pp= y0*(1+2*(qq-x0)/(x1-x0)) * (qq-x1)/(x0-x1) (qq-x1)/(x0-x1)+y1*(1+2*(qq-x1)/(x0-x1)) * (qq-x0)/(x1-x0) * (qq-x0)/(x1-x0) +yd0*(qq-x0) * (qq-x1)/(x0-x1) * (qq-x1)/(x0-x1) +yd1*(qq-x1) * (qq-x0)/(x1-x0) * (qq-x0)/(x1-x0);pDC->SetPixel(qq*500,pp*400,RGB(225,185,15));}}4. 实验截图5. 实验结果分析:分析：分段线性插值的方法克服了Lagrange插值法当节点不断加密时，构造的插值多项式的次数不断升高，高次多项式虽然是连续的，但是不一定都收敛到相应的被插函数而产生Runge现象。

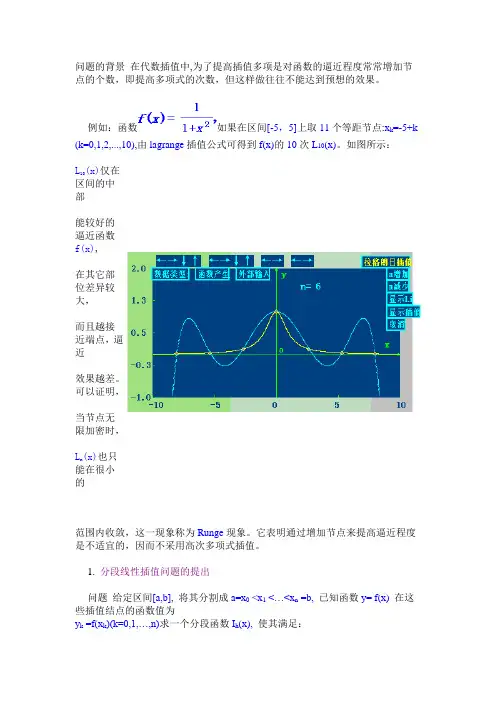
问题的背景在代数插值中,为了提高插值多项是对函数的逼近程度常常增加节点的个数，即提高多项式的次数，但这样做往往不能达到预想的效果。

例如：函数如果在区间[-5，5]上取11个等距节点:x k=-5+k (k=0,1,2,...,10),由lagrange插值公式可得到f(x)的10次L10(x)。

如图所示：L(x)仅在10区间的中部能较好的逼近函数f(x),位差异较大，而且越接近端点，逼近效果越差。

可以证明，当节点无限加密时，L(x)也只n能在很小的范围内收敛，这一现象称为Runge现象。

它表明通过增加节点来提高逼近程度是不适宜的，因而不采用高次多项式插值。

1. 分段线性插值问题的提出问题给定区间[a,b], 将其分割成a=x0 <x1<…<x n =b,已知函数y= f(x)在这些插值结点的函数值为y k =f(x k)(k=0,1,…,n)求一个分段函数I h(x),使其满足：(1) I h(x k )=y k，(k=0,1,…,n) ;(2) 在每个区间[x k ,x k+1 ]上,I h (x)是个一次函数。

易知,I h(x)是个折线函数, 在每个区间[x k ,x k+1 ]上,(k=0,1,…,n)于是, I h (x)在[a,b]上是连续的，但其一阶导数是不连续的。

一、分段线性函数的基函数我们从整体上来构造分段线性函数的基函数。

每个插值结点上所对应的插值基函数l i(x)应当满足：(1)l i(x)是分段线性函数；对于i=0，其它点上，l0(x)=0;对于i=1,2,…,n-1，其它点上，l i(x)=0;对于i=n，其它点上，ln(x)=0.于是，此表达式与前面的表达式是相同的,这是因为在区间[xk ,xk+1]上,只有lk (x),lk+1(x)是非零的，其它基函数均为零。

即I h (x)= yklk(x) + yk+1lk+1(x).例已知函数在区间[0,5]上取等距插值节点(如下表)，求区间上分段线性插值函数,并利用它求出f(4.5)近似值。

分段线性插值法求插值摘要本文根据题目的要求,利用分段线性插值法对采样点和样本值进行插值计算。

为了更好的评断模型的优化性，我们同时采用了最近点插值，3次多项式插值和3次样条插值法来处理同样的问题，作为分段线性插值方法的参考模型。

根据插值函数计算区间内任意取样点的函数值。

最后再利用所得函数值画出相应的函数图象，并与原函数g(x)的图象进行对比。

通过对本题四个问题的解答，并观察对比函数图象我们得到了如下两个重要的结论：（1）在同一取样点，利用不同的插值方法可能会得到不同的函数值，所得函数值与原函数的标准函数值的误差大小决定了该插值方法的“好坏”。

而最优化的插值方法往往依赖于被插值函数。

本题中，在函数式g(x)对应X,Y的条件下，可以根据对比函数图象明显看出：分段线性插值方法和3次多项式插值方法优于3次样条插值和最近点插值。

（2）在插值计算中，取样点的多少往往会影响所得插值函数优化程度。

一般情况下，取样点越多所得插值函数越优化，对应的函数值与标准函数值越接近。

通过对本题四个问题相应对比函数图象的观察，我们也明显看出：在区间[-6 6]内，当取样点为21，41时，分段线性插值法进行插值计算得到的函数图象基本上与原函数g(x)吻合。

AbstractIn this article ,we use piecewise linear interpolation to compute the sampling point and sample value according to the request of question. In order to judge the model's quality in a better way, we use nearest interpolation, cubic interpolation and spline interpolation regarded as the model reference of piecewise linear interpolation to deal the question in the same way at the same time. Then draw the function picture by function value of any sampling point in the interval of interpolating function. Finally, we make a comparison between the original function g(x) image and the interpolating function image.At the base of analysing the final result and comparing the constrastive image . We can summarize two items of important conclusion as follows:(1)At the same sampling point , different interpolating method canobtain different function value. Usually , the optimizationalgorithm depends on the size of error between the objectfunction value .(2) When processing interpolating compute , the number of thesampling point will make an effect on the quality of a model.Commonly, the more multitudinous the sampling points wereused ,the more precise the interpolation model will be .目录一．问题的重述 (1)二．问题的分析 (1)三．问题的假设 (1)四．分段线性插值原理 (2)五．问题的求解 (2)六．插值方法的优劣性分析 (5)附录 (6)一．问题的重述已知211)(xx g +=,66≤≤-x 用分段线性插值法求插值，绘出插值结果图形，并观察插值误差。