计数型(通止规)MSA测量系统分析

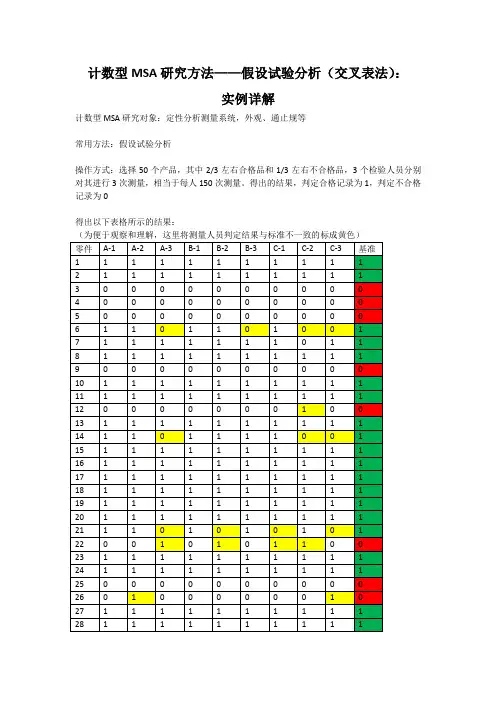
计数型MSA研究方法——假设试验分析（交叉表法）：实例详解计数型MSA研究对象：定性分析测量系统，外观、通止规等常用方法：假设试验分析操作方式：选择50个产品，其中2/3左右合格品和1/3左右不合格品，3个检验人员分别对其进行3次测量，相当于每人150次测量。

得出的结果，判定合格记录为1，判定不合格记录为0得出以下表格所示的结果：（为便于观察和理解，这里将测量人员判定结果与标准不一致的标成黄色）计数型MSA的指标要求和计算：1、Kappa：判定人员一致性好坏的指标，接收准则：Kappa＞0.75 1.1人员之间的一致性：期望发生的次数：根据判定结果的概率，会发生的次数A判定为0的概率=A判定为0的次数/A判定的总次数=（44+6）/150=0.333 A判定为1的概率=A判定为1的次数/A判定的总次数=（3+97）/150=0.667 B判定为0的概率=B判定为0的次数/A判定的总次数=（44+3）/150=0.313 B判定为1的概率=B判定为1的次数/A判定的总次数=（6+97）/150=0.687A判定为0，同时B判定为0的概率=0.333*0.313=0.104A判定为0，同时B判定为1的概率=0.333*0.687=0.229A判定为1，同时B判定为0的概率=0.667*0.313=0.209A判定为1，同时B判定为1的概率=0.667*0.687=0.458A判定为0，同时B判定为0期望的次数=0.104*150=15.6A判定为0，同时B判定为1期望的次数=0.229*150=34.35A判定为1，同时B判定为0期望的次数=0.209*150=31.35A判定为1，同时B判定为1期望的次数=0.458*150=68.7Po：A与B判定结果一致的概率=（44+97）/150=0.94Pe：期望结果一致的概率=（15.6+68.7）/150=0.562Kappa=== 0.863Kappa＞0.75，说明A与B一致性较好A与C、B与C按相同方式计算并进行判定1.2人员与标准之间的一致性Po=（45+97）/150=0.947Pe=（16+68）/150=0.56Kappa=（0.947-0.56）/（1-0.56）=0.879Kappa＞0.75，说明A与标准一致性较好B、C与标准的一致性按相同方式计算并进行判定2、有效率、漏判率、错判率：判定单个人员好坏的指标有效率：完全判定正确的零件个数/总零件个数漏判率：将不合格判定为合格的次数/标准为不合格的次数（Ⅱ类风险，顾客风险）错判率：将合格判定为不合格的次数/标准为合格的次数（Ⅰ类风险，工厂风险）根据数据计算结果：人员A有效率=42/50=84%人员A漏判率=3/48=6.25%人员A错判率=5/102=4.9%结果表明，人员A有效率位于可接受边缘，漏判率不接受，错判率接受。

莱州市XX机械有限公司作业文件文件编号：JT/C－7.6J－004版号：A/0（MSA）计数型测量系统研究分析作业指导书批准：审核：编制：受控状态：分发号：2015年11月15日发布2015年11月15日实施计数型测量系统研究分析作业指导书 JT/C －7.6J －0041目的为了配备并使用与要求的测量能力相一致的测量仪器，通过适当的统计技术，对计数型测量系统进行分析研究，使测量结果的不确定度已知，为准确评定产品提高质量保证。

2适用范围适用于公司使用的计数型测量仪器的测量系统的分析研究。

3职责3.1检验科负责确定过程所需要的计数型测量仪器，并定期校准和检定，对使用的测量系统进行研究分析，对存在的异常情况及时采取纠正预防措施。

3.2工会负责根据需要组织和安排计数型测量系统分析所需应用技术的培训。

3.3生产科配合对测量仪器进行测量系统分析。

4计数型测量系统简介计数型测量系统是一种测量数值为一有限的分类数量的测量系统，它与能获得一连串数值结果的计量型测量系统截然不同。

通/止规（go/no go gage ）是最常用的量具，它只有两种可能的结果；其它的计数型测量系统，如目视标准，可能产生五到七个分类，如非常好、好、 一般、差、非常差。

所以，针对计量性测量系统所描述的分析方法不能用于评价这样的系统。

当使用任何测量系统进行决策时，都存在一定程度的风险。

这些方法不能量化测量系统变异性，只有当顾客同意的情况下才能使用。

选择和应用于这些技术应以基于一个良好的统计实践，了解影响产品和测量过程变差源，以及错误决定最终顾客的影响。

计数型测量系统的变差来源，应该通过利用了人为因素和人机工程学的研究结果使之最小化。

5研究分析方法5.1某生产过程处于统计受控状态，其性能指数为Pp=PpK=0.5，这是不可接受的。

由于过程正在生产不合格的产品，于是被要求采取遏制措施，以便从生产过程中挑出不可接受的产品。

见图1：图1过程范例5.2具体的遏制行动是，过程小组采用了一个计数型量具，来对每一个零件与一个指定的限定值进行比较。

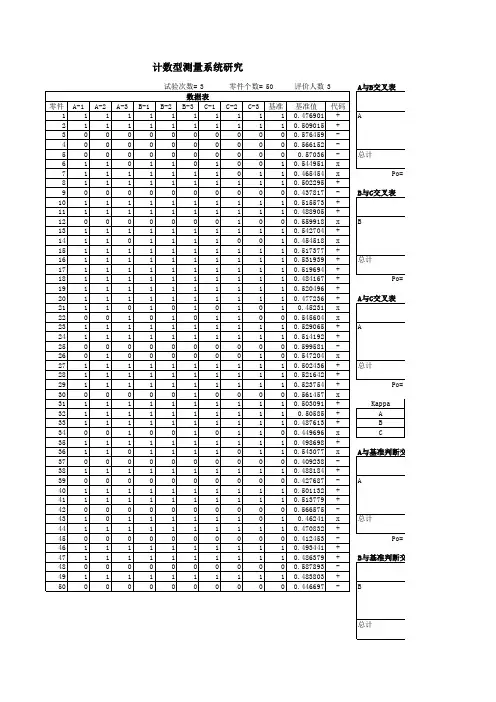
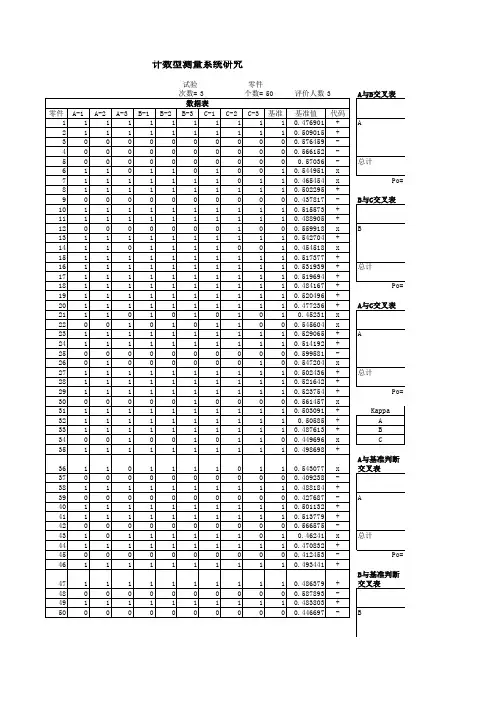
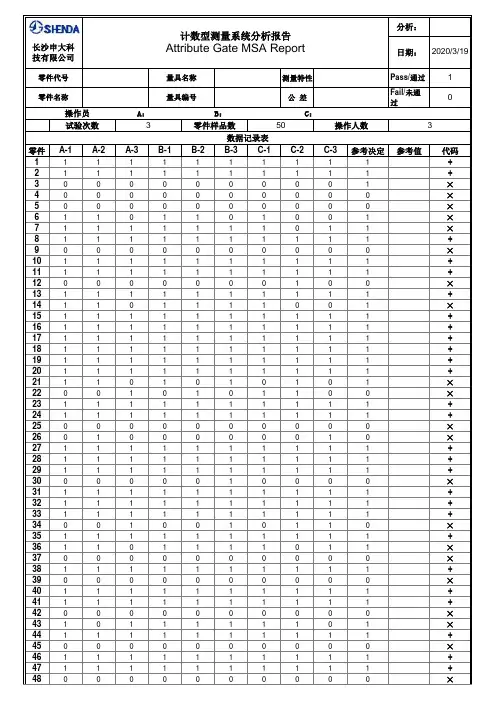
XX 公司计数型MSA 分析报告日 期：实 施 人： 评 价 人：系统名称： 所属工序： 分析结论： 合格 不合格 审 核：批 准：胡梅青、彭春玲、罗玉容 2017年07月19日 张志超印制板外观检验 中间检验计数型MSA分析报告目录有效性 (4)合格品误判率 (4)不合格品错发率 (5)印制板外观检验（中间检验） MSA分析报告一、计数型MSA评测说明所谓计数型MSA就是指计数型测量系统分析，就是让检验员评测覆铜板或印制板的某一项缺陷，并判定检验员评测结果与标准值不一致的严重度是否可接收的一种分析方法。

在计数型测量系统分析中，主要评估：有效性（检验员对样品三次评测结果均与基准值一致的总次数，占样品总数量的比率）、合格品误判率（检验员对基准值为合格的样品，评测为不合格的次数，占基准值为合格样品被评测总次数的比率）、不合格品错发率（检验员对基准值为不合格的样品，评测为合格的次数，占基准值为不合格样品被评测总次数的比率）是否均满足接收要求。

二、试验方案2.1 准备50块印制板，对于这50块印制板，外观合格样品 32 块，外观不合格样品18 块，对每一块样品随机编号，便于对应编号记录检验员每次对样品的评测结果，在让检验员对样品进行检验评测时，不允许检验员知道各个样品的编号。

2.2 2017 年 07 月，选择中间检验工序3位从事外观检验工作的检验人员，在其都不知晓每个试样判定结果前提下，分别让这3位检验人员在不同时间段对每块样品进行3次评测，并将每位检验人员评测结果及样品定义结果分别对应记录，不合格用“0”标记,合格用“1”标记。

三、数据收集表1 计数型测量系统数据收集记录表注：表1中“0”表示不合格，“1”表示合格。

四、测量系统分析结果判定标准4.1 3位评测者Kappa≥0.75,表明测量系统一致性好，否则表示一致性差。

4.2 计数型测量系统有效性、合格品误判率、不合格品错发率结果判定标准如下表2所示。

MSA计数型的实施步骤概述MSA（测量系统分析）是一种用于评估测量系统的准确性、重复性和可再现性的工具。

它能够帮助我们确定测量系统中存在的偏差和变异，并为改进测量系统提供方向。

本文将介绍MSA计数型的实施步骤，以帮助您进行高质量的测量系统分析。

步骤一：确定评估对象首先，我们需要确定要评估的测量系统。

这可以是一个特定的设备、方法或过程。

确保评估对象具有一定的测量范围和精度，以使MSA分析具有实际意义。

步骤二：制定测量计划在开始测量前，我们需要制定一个完整的测量计划。

这包括确定测量的目的、测量方法、测量设备和测量员工等。

确保所有的测量条件和参数都能够准确地复制和记录。

步骤三：收集测量数据在这一步骤中，我们需要进行实际的测量，并记录测量结果。

根据测量计划，挑选一定数量的样本进行测量，确保样本数量足够大以覆盖整个测量范围。

步骤四：计算测量系统的能力指数在这一步骤中，我们需要计算测量系统的能力指数。

这包括计算GRR（测量系统的可重复性与再现性）指标，如Gage R&R、可重复性方差和再现性方差等。

确保准确计算这些指标，以评估测量系统的准确性和重复性。

步骤五：分析数据通过对测量数据的分析，我们可以得出一些结论。

比如，我们可以评估测量系统的稳定性、精确度和可靠性。

同时，我们还可以检查是否存在系统性偏差和变异，并考虑如何提高测量系统的性能。

步骤六：制定改进计划根据数据分析的结果，我们可以制定改进计划。

这包括提出改进测量设备、调整测量方法和执行员工培训等措施。

确保改进计划能够解决测量系统中存在的问题，并提高测量的准确性和重复性。

步骤七：实施改进计划在这一步骤中，我们需要实施制定的改进计划。

这可能涉及到购买新的测量设备、培训测量员工和更新测量方法等活动。

确保改进计划的顺利实施，并监控改进效果。

步骤八：验证改进效果最后，我们需要验证改进计划的效果。

这可以通过重新进行MSA分析来评估测量系统的准确性和重复性是否得到改善。

计数型测量系统分析（MSA）计数型测量系统的最大特征是其测量值是一组有限的分类数，如合格、不合格、优、良、中、差、极差，等等。

当过程输出特性为计数型数据时，测量系统的分析方法会有所不同，一般可以从一致性比率和卡帕值两个方面着手考虑计数型测量系统分析。

➢计数型测量系统分析——一致性比率一致性比率是度量测量结果一致性最常用的一个统计量，计算公式可以统一地概括为：一致性比率=一致的次数/测量的总次数根据侧重点和比较对象的不同，又可以分为4大类。

1. 操作者对同一部件重复测量时应一致，这类似于计量型测量系统的重复性分析。

每个操作者内部的计数型测量系统都有各自的一致性比率。

2. 操作者不但对同一部件重复测量时应一致，而且应与该部件的标准值一致（若标准值已知），这类似于计量型系统的偏倚分析。

将每个操作者的计数型测量系统的结果与标准值相比较、分析，又有各自不同的一致性比率。

3. 所有操作者对同一部件重复测量时应一致，这类似计量型测量系统的再现性分析，操作者计数型测量系统分析之间有一个共同的一致性比率。

4. 各操作者不但对同一部件重复测量时应一致，而且应与该部件的标准值一致（若标准值已知）。

通常，使用这种一致性比率来衡量计数型测量系统的有效性。

一般说来，一致性比率至少要大于80%，最好达到90%以上。

当值小于80%，应采取纠正措施，以保证测量数据准确可靠。

➢计数型测量系统分析——卡帕值（k）K（希腊字母，读音kappa，中文为卡帕）是另一个度量测量结果一致程度的统计量，只用于两个变量具有相同的分级数和分级值的情况。

它的计算公式可以统一的概括为：以上公式中，P0为实际一致的比率；P e为期望一致的比率。

K在计算上有两种方法：Cohen 的k和Fleiss的k。

K的可能取值范围是从-1到1，当k为1时，表示两者完全一致；k为0时，表示一致程度不比偶然猜测好；当k为-1时，表示两者截然相反，判断完全不一致。

通常，k为负值的情况很少出现，下表归纳了常规情况下k的判断标准。

MSA测量系统分析及改善1. 简介测量系统分析（Measurement System Analysis，简称MSA）是一种用于评估和改善测量系统准确性和可重复性的工具。

在许多行业中，测量系统是至关重要的，因为它们用于确定产品和过程的质量或性能。

然而，如果测量系统本身存在问题，那么得到的测量结果可能是不可靠的。

因此，MSA是确保测量系统可靠性的关键步骤。

本文将介绍MSA的基本概念，并提供一些建议和技术，以帮助您进行测量系统分析和改善。

2. MSA的重要性准确和可靠的测量系统对于生产和质量控制至关重要。

它们用于确定产品和过程的性能，并对产品的质量提供有价值的信息。

然而，一个不准确或不可靠的测量系统可能会导致以下问题：•不准确的测量结果，导致错误的决策和行动；•不一致的测量结果，使得无法比较不同时间或不同地点的测量结果；•高度可变的测量结果，使得很难确定产品或过程的真实性能；•长期而言，测量系统的不准确性和不稳定性可能导致质量问题和高成本。

因此，MSA对于确保测量系统的可靠性和准确性非常重要。

3. MSA的步骤进行MSA时，可以遵循以下基本步骤：3.1 确定测量系统首先，需要明确要评估和改善的测量系统。

这可能是一个简单的工具，如一个尺子，也可能是一个复杂的设备，如一个坐标测量机。

3.2 确定评估指标接下来，需要确定用于评估测量系统准确性和可重复性的指标。

常见的评估指标包括偏差、重复性、线性度和分辨率等。

3.3 收集数据然后，需要收集测量系统的实际数据。

这可以通过对已知样本进行测量来实现。

确保数据的收集尽可能地全面和代表性。

3.4 数据分析一旦数据收集完毕，就可以进行数据分析。

常见的数据分析方法包括范围分析、方差分析和回归分析等。

通过这些分析方法，可以确定测量系统的准确性和可重复性情况。

3.5 制定改善计划根据数据分析的结果，制定改善计划以提高测量系统的准确性和可靠性。

这可能涉及校准设备、培训操作员或更换测量设备等。

MSA测量系统分析报告1. 引言测量系统分析（Measurement System Analysis，简称MSA）是指对用于测量和判断产品性能或特征的测量设备和方法进行评估和分析的过程。

MSA的目标是确认测量系统的可靠性和准确性，以确保其能提供可靠且准确的测量结果。

本报告将对某一特定的MSA测量系统进行分析，并评估其性能和准确性。

2. 测量系统描述2.1 测量系统的目的和背景该测量系统用于检测某一机械零件的尺寸。

此测量系统的目的在于确保机械零件的尺寸符合规定的标准要求，以确保零件的质量和性能。

2.2 测量设备描述该测量系统使用一台数字卡尺作为测量设备，该卡尺具有高精度和快速测量的特点。

卡尺具有显示屏和刻度尺，可以直接读取并显示测量结果。

3. 数据收集与分析为了评估测量系统的准确性和可靠性，我们采集了一组样本进行测量。

每个样本由同一机械零件的尺寸组成，共采集了50个样本。

我们使用卡尺对每个样本进行了三次重复测量，并记录下每次测量的结果。

下表是我们采集的样本数据：样本编号测量1 (mm) 测量2 (mm) 测量3 (mm)1 25.02 25.03 25.042 24.99 25.00 25.013 25.01 24.99 25.00…………50 24.98 24.97 24.993.1 重复性分析重复性是指在相同的测量条件下，重复测量的结果是否一致。

为了评估测量系统的重复性，我们计算了每个样本的测量值之间的标准偏差（Standard Deviation, SD）。

标准偏差越小，说明测量系统的重复性越好。

下图是测量值的标准偏差的概率分布图：Sample | Standard Deviation (mm)-------|-------------------1 | 0.012 | 0.023 | 0.01... | ...50 | 0.01从概率分布图中可以看出，大多数样本的标准偏差都在0.01mm左右，说明测量系统的重复性非常好。

测量系统分析（MSA）作业指导书1．目的 :对所有量具、量测及试验设备实施统计分析, 藉以了解量具系统之准确度与精确度。

2. 范围 :所有控制计划（Control Plan）中包含的/或客户要求的各种量测系统均适用之.3.定义 :3.1 MSA:量测系统分析3.2 量具：是指任何用来获得测量结果的装置。

经常是用在工厂现场的装置，包括通/止规（go/no go device)。

3.3 量测系统：是对测量单元进行量化或对被测的特性进行评估，其所使用的仪器或量具、标准、操作、方法、夹具、软件、人员、环境和假设的集合；也就是说，用来获得测量结果的整个过程。

3.4量具重复性(EV) : 一个评价人多次使用一件测量仪器，对同一零件的某一特性进行多次测量下的变差。

3.5 量具再现性(AV) : 由不同的评价人使用相同的量具，测量一个零件的一个特性的测量平均值的变差。

3.6偏性：同一人使用同一量具在管制计划规划地点与在实验室量测同一产品之相同特性所得平均值与真值之间的差异。

3.7稳定性：指同一量具于不同时间量测同一零件之相同特性所得之变异。

3.8线性：指量具在预期内之偏性表现。

4.权责:4.1量测系统测试的排定、数据分析、仪器操作人员的选择：品保部4.2测试执行：各相关单位4.3 MSA操作人员的培训：品保部5. 执行方法5.1 QA工程师人员依公司PCP文件建立《xx年MSA实施计划表》或客户要求,并依据计划表之排程进行对仪器做量测系统分析。

5.2 取样方法：5.2.1计量型取样：从代表整个工作范围的过程中随机抽取10件样品，但所抽取的10件样品其数值必须涵盖该产品过程分布（也可用之前类似过程的过程能力或者过程标准差代表TV进行计算）。

5.2.2计数型取样：取50PCS样品，其中包含临近值，不良品与合格品。

5.2.3.测量过程中需要考虑盲测，由2或3个测量者随机抽取对每个产品各测量取一定数量样品.5.3计数型:5.3.1被评价的零件的选定随机抽取50个零件，把零件编号，由研究小组给出该50个零件的标准，必须含合格，不合格，模糊品，条件允许的情况下最好各占1/3。

XXXX有限公司测量系统分析（MSA）指导书文件编号：版本：编制：审核：批准：XXX有限公司发布测量系统分析（MSA）作业指导书1目的：评价整个测量系统（即操作、程序、量具、设备、软件及操作人员的集合）是否具有可接受的测量水平，判定该测量系统是否适用。

2确定方法：2.1计量型量具（如游标卡尺）采用均值和极差法研究量具的重复性和再现性。

2.2计数型量具（如通止规），采用信号探测法或假设检验分析法研究。

2.3根据类型确定相应的计量型或计数型量具或设备，选择相应的研究方法3测量设备选购3.1测量系统必须有足够的灵敏性：3.1.1仪器要具有足够的分辨力：应至少保证仪器的分辨力能将公差分成十份或更多，即第一准则应至少是被测范围的十分之一，最好是保证为过程变差的十份之一。

3.1.2仪器要具有有效的分辨力：应保证仪器对所探测的产品或过程变差在一定的应用及环境下的变化具有足够的灵敏性。

3.2测量系统必须是稳定的：3.2.1在重复性的条件下，仪器变差只归因于普通原因而不是特殊原因。

3.2.2测量分析者必须经常考虑到仪器的稳定性对实际应用和统计的重要性。

3.3统计特性（误差）在预期的范围内一致，并足以满足测量的目的（产品或过程控制）。

4测量系统分析过程4.1采用均值和极差法研究量具的重复性和再现性指导：4.1.1准备工作：4.1.1.1确定评价人数量、被测零件、样品数量及重复读数次数。

4.1.1.1.1评价人：应从日常操作该仪器的人中选择，并且采用盲测（即选定评价人事先不知道本次研究事件），评价人数量至少为3人。

4.1.1.1.2被测零件：零件应从过程中选取并能代表整个工作范围。

对会直接影响测量结果的缺陷零件不应选用。

4.1.1.1.3样品数量和重复读数次数：零件样品数量至少应为5个，重复读数次数即试验次数至少为2次。

对每一个零件进行编号、定位。

注：对大或重的零件可选较少的样品和较多试验次数4.1.1.2制定操作程序和应用表格4.1.1.2.1确保每一位评价人都采用相同的方法，按规定的测量步骤测量特征尺寸。

【质量工具干货】一文悟透测量系统分析（MSA）在日常生产中，我们经常根据获得的过程加工部件的测量数据去分析过程的状态、过程的能力和监控过程的变化；那么，怎么确保分析的结果是正确的呢？我们必须从两方面来保证，一是确保测量数据的准确性/质量，使用测量系统分析（MSA）方法对获得测量数据的测量系统进行评估；二是确保使用了合适的数据分析方法，如使用SPC工具、试验设计、方差分析、回归分析等。

下面主要针对测量系统分析（MSA）来进行讲解。

01何为测量系统？定义：是对测量单元进行量化或对被测的特性进行评估，其所使用的仪器或量具，标准，操作，方法，夹具，软件，人员，环境及假设的集合。

也就是说，用来获得测量结果的整个过程。

由这一定义可以将测量过程看作一个制造过程，其产生的输出就是数值（数据）。

这样看待一个测量系统时很有用的，因为这样让我们明白已经说明的所有概念，原理，工具，这在统计过程控制中早已被证实它们的作用。

检验本身就是一个过程。

02为什么要对测量系统进行分析？测量数据的质量：数据的质量取决于测量的统计特征：偏倚及变差。

高质量数据——对某一特定特性值进行多次测量的数值均与该特性的参考值“接近”。

低质量数据——测量数据均与该“特性”的参考值相差“很远”。

理想的测量系统不存在，为什么？由于测量系统变差源：标准，人员（评价人）。

仪器（量具），工作件（零件），程序（方法），环境的作用结果，使得观测到的过程变差值与实际变差值不相等。

03对测量系统分析要分析什么？前面我们谈到，数据的质量取决于稳定条件下进行操作的测量系统中，多次测量的统计特征：偏倚和变差。

为此，我们引申出如下一些术语：1.位置变差◆偏倚：观测到的测量值的平均值与参考值之间的差值。

◆准确度：与真值（或参考值）“接近”的程度。

◆稳定性：别名“漂移” 随时间变化的偏倚值。

◆线性：在量具正常工作量程内的偏倚变化量。

2.宽度变差◆精确度：每个重复读数之间的“接近”程度。

测量系统分析（MSA）计数型测量系统研究计数型测量系统研究计数型测量系统属于测量系统中的一类，是一种测量数值为有限的分类数量的测量系统，它与测量结果是连续值的计量型测量系统不同。

最常见的是通过/不通过量具，只可能有两个结果；其它的计数型测量系统，如目视标准，可能产生5~7个分级，如非常好、好、一般、差、非常差等。

MSA前面所介绍的分析方法不能被用来评价这样的系统。

计数型测量系统研究计数型量具的特点是，把每一个零件同一个特定的限定值进行比较。

如果满足限定值就接受这个零件，反之拒绝零件（如通过/不通过量具）。

多数这种类型的量具以一套标准零件为基础进行设定接受与拒绝。

与计量型量具不同的是，这个计数型量具不能指出一个零件有多好或多坏，只能指出零件可接受或拒绝。

计数型测量系统研究-范例计数型测量系统研究-范例表格中的“1”指定为可接受判断，“0”指定为不可接受判断。

表格中的基准判断和计量基准值不预先确定。

表格中的“代码”列还用“-”、“+”、“x”显示了零件是否在第Ⅲ，Ⅱ，Ⅰ，区域。

计数型测量系统研究-范例假设检验分析-交叉表方法由于研究人员不知道零件的基准判断值，他们开发了交叉表比较每个评价人之间的差异。

计数型测量系统研究-范例2016-11-24陈瑞泉8表中（期望的计算）值的计算过程如下：(44+3)(3+97)/150=31.3(6+97)(97+3)/150=68.7(3+44)(44+6)/150=15.7(97+6)(6+44)/150=34.3计数型测量系统研究-范例上述这些表格的目的是确定评价人之间意见一致的程度。

为了确定评价人一致的水平，研究人员用科恩的Kappa来测量两个评价人对同一目标评价值的一致程度。

1值表示完全一致，0值表示一致程度不比偶然的要好。

kappa只用于两个变量具有相同的分级值和相同的分级数的情况。

计数型测量系统研究-范例kappa是一个评价人之间一致性的测量值。

检验是否沿对角线格子中的计数（接收比率一样的零件）与那些仅是偶然的期望不同。

如何对检具进行测量系统分析？QS-9000是美国三大汽车公司为统一供应商质量管理体系而推行的采购要求。

出于美国汽车工业的影响和地位，QS-9000在世界范围内被广泛推广运用，尤其是为整车生产企业提供零部件、生产材料及加工的企业。

随着ISO9000标准被国内各行业广泛采用，近几年来，QS-9000作为体现汽车行业特点的质量体系标准，也逐渐得到了国内汽车行业的认同。

国内主要整车生产企业在以ISO9000质量体系作为对其供应商要求的基础上，增加了许多特殊要求，一些整车生产企业对其供应商提出了按QS-9000建立质量体系的要求，并以此作为决定供应商配套资格或其采购份额的条件。

本人在QS-9000认证审核中，发现以下问题较为普遍，在此提出，以供参考。

一、关于标准要求1、可行性评审可行性评审在什么阶段进行，应评审那些内容？标准中对可行性评审的要求是：“供方在签定生产某种产品合同之前，应研究并确定该产品的制造可行性。

……可行性评审应采用产品质量先期策划和控制计划（APQP）参考手册中…小组可行性承诺‟来形成文件”。

首先，从以上内容可知，可行性评审是在签定合同之前进行的。

APQP参考手册在产品开发所经历的五个阶段中第二阶段2.13条对…小组可行性承诺‟作出解释。

如果供应商承担设计责任，那么，所有的设计过程都可理解为为满足顾客要求所进行的合同评审过程。

由于产品设计和过程开发是同步进行的，在产品图样和/或规范输出后，过程开发也到了一定阶段，这时，横向协调小组通过对产品图样和/或规范以及过程阶段性开发输出结果的分析，对产品是否满足顾客的要求、设备和工装成本、材料、过程能力等内容进行评审，从而对产品制造可行性进行判定。

可行性评审可视为合同评审的一部分。

2、分承包方的零件批准（PAP）标准中规定供方应对其分承包方采用一种零件批准程序，批准的方法可按PPAP或其它零件批准（PAP）进行。

一个企业的分承包方可能会涉及到提供零部件和原材料的不同供方。