当前位置：文档之家 › 圆心角、弧、弦、弦心距之间的关系ppt

圆心角、弧、弦、弦心距之间的关系ppt

  • 格式：ppt
  • 大小：241.50 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

人教版数学九年级上册圆周角的概念和圆周角的定理ppt课件

人教版数学九年级上册圆周角的概念和圆周角的定理ppt课件
（2）在同圆或等圆中，相等的圆周角所对的弧 相等。
AB
C′
C
E
O
C
F
DF
B' O′
B O
A'
A
【方法一点通】 利用圆周角定理及其推论证明时常用的思路
1.在同圆或等圆中,要证弧相等,考虑证明这两条弧所对的圆周角
（圆心角、弦、弦心距）相等.
2.在同圆或等圆中,要证圆周角相等,考虑证明这两个圆周角所对 的弧（圆心角、弦、弦心距）相等.
圆周角定理推理2
同圆或等圆中，相等的圆周角所对 的弧相等
条件“在 同圆或等 圆中”可以 省略吗？
C′
C
B' O′
B O
A'
A
知识要点 圆周角定理的推理
1、（在同圆或等圆中），同弧或等弧所 对的圆周角相等．
2、 在同圆或等圆中，如果两个圆周角相等，
它们所对的弧一定相等
A
C
B
·
·
D
E
正确理解圆心角，弦、 弦心距、圆周角与弧 的互推关系
知一推四 前提：同圆 或是等圆中
正确理解圆心角，弦、 弦心距、圆周角与弧 的互推关系
课后练习. P88 第3,4题.
谢谢大家!
课后作业
1． 已知：A⌒C = B⌒D， A
B
求证：AB∥CD． C
D
2.AB、AC为⊙O的两条弦，延长CA到D，使 AD=AB，如果∠ADB=35° ，求∠BOC的度数。
⌒⌒ AB=A′B′
C′
B A′
B′ O′
人教版数学九年级上册圆周角的概念 和圆周 角的定 理p p t 课件
五、定理
圆周角定 理
在同圆或等圆中，一条弧(同弧或等弧)

圆心角弧弦弦心距之间关系

圆心角弧弦弦心距之间关系

（5）要证AB=CD，必须有 OE=OF 或 AB = CD 或 ∠AOB=∠COD O
F
C
D
例1：如图点O是∠EPF的平分线上的一点，以O 为圆心的圆和角的两边分别交于点A、B和C、D
求证：AB=CD
证明：作OM⊥AB，ON ⊥CD，MN分别为垂足。
∠MPO= ∠NPO
OM ⊥AB ON ⊥CD OM=ON
圆心角、弧、弦、弦心距之间的关系
一、定义
B′ M′
A′
1、圆心角：顶点在圆心的角。
2、弦心距：圆心到弦的距离。
O
二、定理
AM
B
在同圆或等圆 中，相等的圆心角所对的弧相等，所对的 弦相等，所对的弦的弦心距相等。
三、推论：
在同圆或等圆中，如果两个圆心角、两条弧、两条弦或 两条弦的弦心距中有一组量相等，那么它们所对应的其余各 组量也分别相等。
命题三：
条件：在同圆或等圆中 结论：
圆心角所对弦的弦心
圆心角相等 圆心角所对的弧相等 圆心角所对弦的弦心距相等
圆心角所对的弦相等 圆心角相等 圆心角所对弦的弦心距相等
圆心角所对的弦相等 圆心角所对的弧相等 圆心角相等
距相等
题组二：
已知：如图AB、CD是⊙O的两条弦，OE、OF为AB、CD的弦心 距，请根据所学内容填空：
题组2
题组一：
如图： ∵∠AOB= ∠A’OB’ ∴A’B’=AB，A’B’= AB 你认为正确吗？为什么？
O
A’
B’
A
B
定 理：
条件：在同圆或等圆中
命题一： 圆心角相等
圆心角所对的弦相等
结论： 圆心角所对的弧相等
圆心角所对弦的弦心距相等

弧弦圆心角课件

弧弦圆心角课件

应用三：求解多边形内角和
弧弦圆心角定理
多边形内角和等于（n-2）×180°，其中n为多边形的边数。
弧弦圆心角在多边形中的应用
通过弧弦圆心角定理，可以求解多边形内角和，进而解决与多边形内角相关的问题。同时，也可以利 用多边形内角和的求解方法，推导其他几何图形的内角和公式。
05
弧弦圆心角在三角函数中应用
心角之差。
弧弦圆心角在波动中的应用
02
利用弧弦圆心角可以直观地表示波动的相位，从而方便地描述
两个波之间的相位差以及波的干涉、衍射等现象。
应用实例
03
利用弧弦圆心角分析两个同频率波的干涉现象，可以方便地得
出干涉加强或减弱的条件。
应用三：描述圆周运动中角速度与线速度关系
角速度与线速度关系
在圆周运动中，角速度与线速度之间的关系可以通过弧弦圆心角来描述。具体地，角速度 等于单位时间内转过的弧弦圆心角所对应的弧度数，而线速度则等于角速度与半径的乘积 。
要点二
利用弧弦圆心角关系判断三角函 数方程的解的存在性
在解三角函数方程时，有时需要判断方程是否有解。此时 ，可以利用弧弦圆心角关系来判断方程是否有解。例如， 当方程中的三角函数值超出其定义域时，可以判断该方程 无解。
06
弧弦圆心角在物理中应用
应用一：描述简谐振动中相位差
相位差定义
两个同频率简谐振动的相位之差，等于它们所对应的弧弦圆心角 之差。
。
性质定理二
在同圆或等圆中，如果两条弧相等 ，那么它们所对的圆心角相等，所 对的弦也相等。
性质定理三
在同圆或等圆中，如果两条弦相等 ，那么它们所对的弧相等，所对的 圆心角也相等。
判定方法二：利用三角函数判定

圆心角、弧、弦、弦心距之间的关系PPT演示课件

圆心角、弧、弦、弦心距之间的关系PPT演示课件

AOB COD AB=CD ，_____________ ． AB = CD ，那么____________ AB=CD AB = CD ，_________ （3）如果∠AOB=∠COD，那么_____________ ．
（2）如果
（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？ 为什么？ OE﹦OF
证明：∵ OE⊥AB OF ⊥CD A E O B D
17
∵ AB﹦CD ∵ OA﹦OC
∴ AE﹦CF ∴ Rt△AOE≌Rt △COF C
·
F
∴ OE﹦OF
1°弧的概念：
顶点在圆心的圆心角等分成 360 份时，每 一份的圆心角是 1°的角，整个圆周被等分成 360份，我们把每一份这样的弧叫做1°的弧。 （同圆中，相等的圆心角所对的弧相等）
10
圆心角、弧、弦、弦心距之间的关系
在自己的圆内作两条长度相同的弦，量 一量它们所对的圆心角
D B C
O A
11
圆心角、弧、弦、弦心距之间的关系
两位同学作一条长度相同的弦，看一 看它们所对的圆心角是否相同
B O A
O' B' A'
12
(2) 推论： 在同圆或等圆中,如果两个圆心角、两条弧、 两条弦或两条弦的弦心距中有一组量相等， 那么它们所对应的其余各组量都分别相等。
B′
┏ A′ D′
④ OD=O′D′
15
试一试你的能力
一.判断下列说法是否正确：
1相等的圆心角所对的弧相等。（ ×）
2相等的弧所对的弦相等。（ √ ）
B
二.如图，⊙O中，AB=CD,
50 o . 1 50，则 2 ____

3.2圆的对称性(2)圆心角,弧,弦,弦心距之间的关系

3.2圆的对称性(2)圆心角,弧,弦,弦心距之间的关系
A A
D D
●
B
O
B
●
O
●
O′
┏ A′ D′ B′ 由条件: 由条件: AOB=∠ ①∠AOB=∠A′O′B′
可推出
┏ A′ D′ B′ ⌒ ⌒ ②AB=A′B′ ③AB=A′B′ ④ OD=O′D′
猜一猜
拓展与深化
在同圆或等圆中,如果轮换下面五组条件: 同圆或等圆中 如果轮换下面五组条件: 两个圆心角, 两条弧, 两条弦, ①两个圆心角,②两条弧,③两条弦,④两条弦心 你能得出什么结论? 距,你能得出什么结论?与同伴交流你的想法 和理由. 和理由.
B′
M′
A′
O M A
B
O
B(B′)
M′
M A ( A ′)
想一想
圆心角
圆心角, 圆心角, 弧,弦,弦心距之间的关系定理
如图,如果在两个等圆⊙ 如图,如果在两个等圆⊙O和⊙O′中,分别作相等 O′中 的圆心角和∠AOB和 A′O′B′,固定圆心 固定圆心, 的圆心角和∠AOB和∠A′O′B′,固定圆心,将其中 的一个旋转一个角度,使得OA和O′A′重合 重合. 的一个旋转一个角度,使得OA和O′A′重合.
九年级数学(下)第三章 《圆》
3.2圆对称性 3.2圆对称性(2) 圆对称性(2) 圆心角, 圆心角,弧,弦,弦心距之间的关系
想一想
圆的对称性及特性 圆的对称性及特性
圆是轴对称图形, 圆是轴对称图形,圆的对称轴是任意一条经过 圆心的直线,它有无数条对称轴. 圆心的直线,它有无数条对称轴. 圆也是中心对称图形,它的对称中心就是圆心. 圆也是中心对称图形,它的对称中心就是圆心. 用旋转的方法可以得到: 用旋转的方法可以得到:
O

圆的对称性(2)圆心角 弧 弦 弦心距之间的关系

圆的对称性(2)圆心角 弧 弦 弦心距之间的关系
A D O E B
知识延伸
2、如图，在⊙O中，AB与BC相等， OD⊥BC，OE⊥AC，垂足分别为D、E， OD=OE 求证：△ABC是等边三角形
A E
B D
O
C
知识延伸
3、已知：弦AB和CD相交于圆内的点P， 且AB＝CD。求证：∠APO＝∠DPO
Ｃ Ｐ
Ｏ Ａ Ｂ Ｄ
拓展提高
1、如图，过⊙O上一点P作两条互相垂直 的弦PA、PB，且PA=PB。 求证：四边形OCPD是正方形
⌒ ⌒
B
抢答题
A 已知：如图，AB，CD是⊙O的两条弦，
E
O D
OE，OF为AB、CD的弦心距，根据这 节课所学的定理及推论填空：
C
F
⌒ ⌒ (1)如果∠AOB=∠COD，那么_____ ， _______ ， _____ OE=OF AB=CD AB=CD ;
⌒ ⌒ ∠ AOB= ∠ COD AB=CD AB=CD （2）如果OE=OF，那么____________，______，______； ⌒ ⌒
O
跟踪练习
１、在⊙O中，若 AB ＝2 CD ，则弦AB 和CD的关系是（ ） A、AB＝2CD B、AB＜2CD C、AB＞2CD D、无法确定
跟踪练习
2.如图：在条件：①∠COA=∠AOD=60°； ②AC=AD=OA；③点E分别是AO、CD的中 点； ④OA⊥CD且∠ACO=60°中，能推出 四边形OCAD是菱形的条件有_____个.
知识要点
推论
在同圆或等圆中,如果①两个圆心角,②两条弧, ③两条弦,④两条弦心距中,有一组量相等, 那么它们所对应的其余各组量都分别相等.
D
A
●
D O
A

圆心角、弧、弦、弦心距之间的关系

圆心角、弧、弦、弦心距之间的关系

B
o
C
D
18
A
把扇形COD绕点O旋转，使OC与
B
OA重合，因∠AOB=∠COD,所以
OD与OB重合，而圆O的半径相 等，因此点C与点A重合，点D 与点B重合，这样AB 与⌒CD就一⌒
o
C
定重合
D
能够重合的两条弧称为等弧或者说这两条弧相等
半径长相等的两个圆一定能够重合，我们把半径长 相等的两个圆称为等圆
2
3
1、判别下列各图中的角是不是圆心角，并说明理由。
①
②
③
④
4
下面我们一起来观察一下：在⊙O中有哪些圆心角？
如果： ∠AOB=∠
A
COD
B
o C
D 5
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图： ∠AOB=∠
A
COD
B
o C
D 6
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，
所对的弦也相等。
19
ＡB=CD吗？
弧AB与弧CD呢？
Ａ Ｂ
Ｃ Ｄ
O
20
圆心角定理：
在同圆或等圆中，相等的圆 心角所对的弧相等，所对的 弦也相，等所对的弦的弦心距也 相等
弦AB和弦ＣＤ 对应的弦心距 什么关系？
A Ｅ B
o
C Ｆ D
21
22
23
B
o
C
D 10
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
o
C
D 11

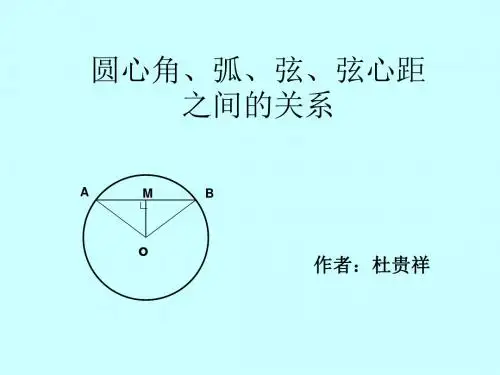
圆心角、弧、弦、弦心-36页PPT精选文档

圆心角、弧、弦、弦心-36页PPT精选文档

(( ((
( (
( (
（1）如果AB＝CD ,那么O_E_=O_F_,_AB_=_C_D,∠__AO_B_=_∠_C_O_D
（2）如果OE＝OF，那么A_B_=_CD_,A_B_=_C_D,_∠_A_O_B_=_∠_C_OD （3）如果AB＝CD，那么_A_B_=C_D,_O_E_=O_F,_∠_A_O_B_=∠_C_O_D
，
M
O
（
∠ＡＯＢ连同AB绕
圆心Ｏ旋转且使射
观察
线ＯＡ与ＯＡ，重合，
发现什么？
，
，
A与A 重合，B 重合
， B
， A
， M
O
（
∠ＡＯＢ连同AB绕
圆心Ｏ旋转且使射
观察
线ＯＡ与ＯＡ，重合，
发现什么？
，
，
A与A 重合，B与B 重合
，，
∵∠AOB=∠AOB
， B
， M
， A
，
∴ 射线OB与OB 重合
由圆的旋转不变性知
圆心角、弧、弦、弦心距 之间的关系
A
M
B
∟
o
作者：杜贵祥
1.举例说明什么是中心对称图形？ 如何判定一个图形是中心对称图形？
A
O A
O
B B
D C
1.举例说明什么是中心对称图形？ 如何判定一个图形是中心对称图形？
A
O A
O
B B
D C
1.举例说明什么是中心对称图形？ 如何判定一个图形是中心对称图形？
A
O A
O
B B
D C
1.举例说明什么是中心对称图形？ 如何判定一个图形是中心对称图形？
A
O A
O

圆心角、弧、弦关系定理

圆心角、弧、弦关系定理

上，且⊙O与角的两边交于A、B、C、D，
求证：AB=CD
B
A P
C
O
M
D B
（1）
变式1：如图（2），∠P的两边与⊙O交与
A
A、B、C、D，AB=CD
P
O
求证：点O在∠BPD的平分线上
C
D
（2）
变式2：如图（3），P为⊙O上一点，PO平分∠APB， 求证：PA=PB
A
P
O
(3) B
变式3：如图（4），当P在⊙O内时，PO平分∠BPD，在⊙中 还存在相等的弦吗？
（2）如果 AB CD，那么____________，_____________
（3）如果∠AOB=∠COD，那么_____________，__
_____________ _______．
（4）如果OE=OF，那么_____________ ，_____________ ，
_____________
推论：
在同圆或等圆中，如果两个圆
心角、两条弧、两条弦或两条弦的 弦心距中有一组量相等，那么它们 所对应的其余的各组量都分别相等。
练习
如图，AB、CD是⊙O的两条弦． OE⊥AB于E，OF⊥CD于F
（1）如果AB=CD，那么___________， _____________ ， _________________。
B
C PO
A
D （４）
1、在同圆或等圆中, 圆心角、弧、弦、 弦心距之间的关系。
2、定理和推论
课堂检测：
课本39页练习1、2
E
D
C
A
o
B
例题选讲
例1 如图, 在⊙O中， AB AC ，∠ACB=60°，

九年级数学上《圆周角》课件新人教版

九年级数学上《圆周角》课件新人教版
C E D A O B
例题
例 如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的 平分线交⊙O于D，求BC、AD、BD的长．
解：∵AB是直径， ∴ ∠ACB= ∠ADB=90°． 在Rt△ABC中，
C
BC AB AC 10 6 8
2 2 2 2
A
O
B
∵CD平分∠ACB，
ACD BCD.
B D
O
C
问题2
若一个多边形各顶点都在同一个圆上，那么， 这个多边形叫做圆内接多边形，这个圆叫做这个 多边形的外接圆。 D B
C
E
O
A
A F
O
C E B
D
返回
问题3
如图：圆内接四边形ABCD中， ∵ ∠A的度数等于弧BCD的一半， ∠BCD的度数等于弧BAD的一半，A 又∵弧BCD+弧BAD 度数为360°， ∴∠A＋∠C＝ 180°.
B
C
E
外角等于它的内对角。
探索结论
先根据图形讨论，然后用语言归纳为 :

性质定理：
D
圆的内接四边形的对角互补，四个内角和为360度， 并且任何一个外角都等于它的内对角。
A
几何表达式： ∵ 四边形ABCD内接于⊙O， ∴ ∠A+∠C=180°且∠B=∠1 .
B
1
E
C
反馈练习：
1、如图，四边形ABCD为⊙O的内接四边 形，已知∠BOD=100°， 则∠BAD= 50º ∠BCD= 130º 2、圆内接四边形ABCD中,∠A:∠B:∠C= B A O D
B
求：∠ACB =
O
B
A
C
2、做一做，成功在向你招手！

-圆心角定理

-圆心角定理

3.已知AB是⊙O的直径，M、N是AO、BO的中 点。CM⊥AB,DN⊥AB,分别与圆交于C、D点。 求证：⌒ ⌒ Ｄ AC=BD
Ａ Ｍ o
●
Ｎ Ｃ
Ｂ
例1 如图在⊙O中，AB=AC ，∠ACB=60°，
⌒ ⌒
求证:∠AOB=∠BOC=∠AOC.
证明：∵AB=AC
⌒ ⌒
AB=AC, △ABC 等腰三角形．
B
M O A
图1
一般的，n。的圆心角对着n。的弧，n。的弧对 着n。的圆心角，即圆心角的度数和它所对的 弧的度数相等。
1、判别下列各图中的角是不是圆心角， 并说明理由。
①
②
③
④
2、下列图中弦心距做对了的是（
）
┐
①
②
┐
③
④
探究
如图， 若∠AOB＝∠A′OB′将圆心角∠AOB绕圆心O旋转到 ∠A’OB’的位置，你能发现哪些等量关系？为什么？ A′ A′ D′ B B D′ B′ B′ D D O
⌒ ⌒ ∠AOB=∠COD OE=OF AB=CD _____________,________,____________。
⌒ ⌒ ∠AOB=∠COD AB=CD AB=CD _____________,________,____________。 ⌒ ⌒ （3）如果AB=CD 那么
∠ AOB=∠COD AB=CD OE=OF ______________,__________,____________ 。
⌒
⌒
┏ A′ D′ B′
③AB=A′B′ ④ OD=O′D′
弧所对的圆心角相等 在同圆或等圆中 如果弧相等 那么 弧所对的弦相等 弧所对的弦的弦心距相等

2圆心角、弧、弦、弦心距之间的关系PPT课件

2圆心角、弧、弦、弦心距之间的关系PPT课件
D
下面我们一起来视察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
o
C
D
下面我们一起来视察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
o
C
D
下面我们一起来视察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
o
C
D
下面我们一起来视察一下圆心角与它所对的弦、弧有什么关系？
A Ｅ B
o
C Ｆ D
解 （2：）（∵1）∠AOB=∠AOC=∠BOC， ∵ AB∠、AAOCB、+B∠CA分O别C+是∠∠BAOOCB=、36∠0°A，OC、 ∠ABOBC=所∠对A的O弦C=，120° ∴弦∠ABBO、CA=C36、0°BC-1的20弦°心-12距0°相=等12。0° 得 ∵∠BCA的O弦B=心∠距A为OC3厘=∠米B，OC ∴AB、=AACC=的BC弦心距为3厘米。
圆心角：以圆心为顶点，以两条半径为边所 组成的夹角。
圆弧：圆上任意两点之间的部分。
圆的任意一条直径的两个端点将圆分成两条弧， 每条弧都叫做半圆。
优弧：大于半圆的弧。
劣弧：小于半圆的弧。 弦：联结圆上任意两点的线段。
过圆心的弦就是直径。
1、判别下列各图中的角是不是圆心角，并说明理由。
①
②
③
④
下面我们一起来视察一下：在⊙O中有哪些圆心角？
半径长相等的两个圆一定能够重合，我们把半径长相 等的两个圆称为等圆。
在同圆或等圆中，相等的圆心角所对的弧相等，所对的 弦也相等。
AB=CD吗？
弧AB与弧CD呢?

27.2圆心角、弧、弦、弦心距之间的关系

27.2圆心角、弧、弦、弦心距之间的关系

27.2圆心角、弧、弦、弦心距之间的关系圆上任意两点之间的部分叫做圆弧，简称弧；联结圆上任意两点的线段叫做弦，过圆心的弦就是直径，以圆心为顶点的角叫做圆心角。

圆的任意一条直径的两个端点将圆分成两条弧，每一条弧都叫做半圆。

大于半圆的⌒，读弧叫做优弧，小于半圆的弧叫做劣弧。

如图27-8，以A、C为端点的劣弧记作AC⌒作“弧AC”；以A、C为端点的优弧记作ABC ，读作“弧ABC”。

如图27-9，⊙O的一个圆心角的两边与⊙O分别相交于点A、B，这个圆心角记作∠AOB，这时，相应得到弧AB和弦AB。

反过来看，对于弧AB或弦AB，相应可作∠AOB。

⌒⌒通常的说AB （或弦AB）是∠AOB所对的弧（或弦），∠AOB是AB （或弦AB）所对的圆心角。

圆心到弦的距离叫做弦心距。

在图27-9中，过圆心O作弦AB的垂线，垂足为C，则垂线段OC的长时弦AB的弦心距。

在平面上，一个圆绕着它的圆心旋转任何一个角度（大于0°且小于360°），都能与原来图形重合。

所以，圆是以圆心为旋转对称中心的旋转对称图形，旋转角可为大于0°且小于360°的任何一个角。

问题1⌒和A`B`⌒如图27-10，在⊙O中，当圆心角∠AOB=∠A'OB'时，它们分别所对的AB是否能重合？把扇形OAB绕圆心O旋转，使OA与OA'重合。

因为∠AOB=∠A'OB'，所以OB ⌒和OB'重合；而⊙O的半径长都相等，因此点A与点A'重合，点B与点B'重合，这样AB⌒就一定重合。

与A`B`⌒与能够重合的两条弧称为等弧，或者说这两条弧相等，上述AB⌒是等弧，记作AB⌒ =A`B`⌒。

A`B`半径长相等的两个圆一定能够重合，我们把半径相等的两个圆称为等圆。

⌒⌒在上述问题中，AB 与A`B` 所对的弦分别是AB和A'B'，通过旋转可知，AB与A'B'重合，两弦的垂线段OC、OC'也重合（为什么），得AB=A'B'，OC=OC'.于是，可以得到圆心角、弦、弦心距之间关系的定理。

圆中知识结构图

圆中知识结构图

关于《圆》的知识结构整理一.主要定理及其作用：1.圆心角，弧，弦，弦心距之间的关系定理：在同圆或等圆中，如果①两个圆心角②两条弧，③两条弦④两条弦心距中，有一组量相等, 那么它们所对应的其余各组量都分别相等：（等弧一等角-一等弦……）用的最多的依据：①在同圆或等圆中，如果两个圆心角相等,那么它们所对的两条弧相等②等弧所对的圆心角相等：③在同圆或等圆中，如果两条弦相等,那么它们所对的两条弧相等④等弧所对的两条弦相等2.垂径定理：如果一条直线①过圆心；②垂直于弦：③平分弦：④平分劣弧：⑤平分优弧•只要具备其中两个条件，就可推岀其余三个结论. （直角三角形一等弧……）用的最多的依据：①垂直于弦的直径平分弦，并且平分弦所的两条弧②平分弦（非直径）的直径垂直于这条弦，并且平分这条弦所对的两条弧.③一条弦的垂直平分线I I经过圆心，并且平分这条弦所对的两条弧④平分弧的直径过圆心的直线垂直平分这条弧所对的弦.3.圆周角定理：（1）直径所对的圆周角是直角：（2） 90°的圆周角所对的弦是直径。

（3）—条弧所对的圆周角等于它所对的圆心角的一半：（4）同弧所对的圆周角相等：（5）等弧所对的圆周角相等：（6）在同圆或等圆中，相等的圆周角所对的弧相等：（等弧——等角——直角三角形）4.切线的性质定理：圆的切线垂直于经过切点的半径（直径）。

（垂直关系）5.切线的判定定理：经过半径的外端，并且垂直于这条半径的直线是圆的切线O6.切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。

（等弦一-等弧一-等角）7.相切和相交两圆的性质定理：如果两圆相切，连心线必过切点。

如果两圆相交，连心线垂直平分公共弦二.主要辅助线及其作用：1.作弦心距：弦的中点.弧的中点。

2.过某一点作弦：构造相等的圆周角。

3.作直径：构造直角三角形和同弧所对的圆周角。

4.连结过切点的半径：“题中若有圆切线圆心切点连一连”。

圆心角、弧、弦、弦心距之间的关系

圆心角、弧、弦、弦心距之间的关系

2圆心角、弧、弦、弦心距之间的关系.(总21页)-本页仅作为预览文档封面，使用时请删除本页-2圆心角、弧、弦、弦心距之间的关系教学目标1．使学生理解圆的旋转不变性，理解圆心角、弦心距的概念；2．使学生掌握圆心角、弧、弦、弦心距之间的相等关系定理及推论，并初步学会运用这些关系解决有关问题；3．培养学生观察、分析、归纳的能力，向学生渗透旋转变换的思想及由特殊到一般的认识规律．教学重点和难点重点;圆心角、弧、弦、弦心距之间的相等关系；难点;从圆的旋转不变性出发，推出圆心角、弧、弦、弦心距之间的相等关系．2圆心角、弧、弦、弦心距之间的关系一、创设情景，引入新课圆是轴对称图形．圆的这一性质，帮助我们解决了圆的许多问题．今天我们再来一起研究一下圆还有哪些特性．1．动态演示，发现规律图7－47，并动态显示：平行四边形绕对角线交点O旋转180°后．(1)结果怎样？(2)这样的图形叫做什么图形？图7－48，并动态显示：⊙O绕圆心O旋转180°．，归纳出：圆是以圆心为对称中心的中心对称图形．让学生观察发现什么结论？得出：不论绕圆心旋转多少度，都能够和原来的图形重合．进一步演示，让圆绕着圆心旋转任意角度α，知识点一、圆的旋转不变性于是归纳总结，得出圆所特有的性质：圆的旋转不变性．即圆绕圆心旋转任意一个角度α，都能够与原来的图形重合．知识点二、弧、弦、圆心角的关系1.圆心角定义如图所示，∠AOB的顶点在圆心，像这样顶点在圆心的角叫做圆心角(central angle),从圆心到弦的距离叫做弦心距2.定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．已知；在⊙O中求证；3.推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等．在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等．要点诠释：(1)一个角要是圆心角，必须具备顶点在圆心这一特征.(2)注意定理中不能忽视“同圆或等圆”这一前提.4推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等．注意：要正确理解和使用圆心角定理及推论。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

P、O的直径为MN，∠APO=∠ CPO 。
求证：PB＝PD
A
M
C P
O
D
B 精选课件ppt
N
9
已知：如图，AD=BC. 求证：AB＝CD
C
A
E
O
B
D
精选课件ppt
10
如图，AB、CD是⊙O的两条弦， OE、OF为AB、CD的弦心距，
如果AB＝CD，那么 ， ，
；
如果OE＝OF，那么 ， ，
（如：OC）
O
C
B
精选课件ppt
3
如图，∠AOB＝∠A`OB`，OC⊥AB， OC`⊥A`B`。
猜想：弧AB与弧A`B`，AB与A`B`， OC与OC`之间的关系，并证明你的猜想。
A
定理 在同圆或等圆中，
C
相等的圆心角所对的弧相等， O
所对的弦相等，所对的弦的
B
弦心距相等。
A' C'
精选课件ppt
；
如果弧AB＝弧CD，那么 ， ， ；
如果∵∠AOB＝∠COD，那么 ， ， 。
A
E
注意前提：
O
B
在同圆或等圆中
C
D
F
下列说法正确吗？为什么？
在⊙O和⊙O’中，∵∠AOB＝∠A’O’B’∴AB＝A’B’
在⊙O和⊙O’中，∵A精B选课＝件pApt’B’，∴弧AB＝弧A’B’ 11
把顶点在圆心的周角等分成360份时，每一 份的圆心角是1°的角。1°的圆心角所对的 弧叫做1°的弧。
n°弧
C
一般地，n°的圆心
角对着n°的弧。
D
n°圆心角
圆心角的度数
O
A
1°圆心角 B
1°弧 和它所对的弧 的度数相等。
精选课件ppt
12
判断题：在两个圆中，分别有弧AB和弧CD，若弧 AB和弧CD的度数相等，则有：
（1）弧AB和弧CD相等；
（）
（2）弧AB所对的圆心角和弧CD所对的圆心角相等。 （）
4
B'
()
题设
在
同
前 提
圆 或 等
圆
中
（ 条 件 ）
圆 心 角 相 等
结论
圆心角所对的弧相等， 圆 心角所对的弦相等， 圆心 角所对弦的弦心距相等。
推论 在同圆或等圆中， 如果两个圆心角、两条弧、 两条弦或两条弦的弦心距中有 一组量相等，那么它们所对应 的其余各组量都分别相等。
精选课件ppt
5
已知：如图，点P在⊙O上,点O在∠EPF的平分 线上，∠ EPF的两边交⊙O于点A和B。 求证：PA=PB.
注意：等弧的度数一定相等，但 度数相等的弧不一定是等弧！
精选课件ppt
13
1、已知：在⊙O中，弦AB所对的劣弧为 圆的1/3，圆的半径为2cm。求AB的长。
2、已知AB和CD为⊙O的两条直径，弦EC//AB, 弧EC的度数为40°，求∠BOD的度数。 E
A
C
O
D
B
精选课B＝PD. 求证： AB=CD 。
精选课件ppt
17
5、已知：如图， ⊙O的两条直径AB⊥CD，四 条弦AE//FD//CG//HB。
求证：E、F、H、G四等分圆周。 D
E
G
A
F
精选课件ppt
O
B
H
C
18
此课件下载可自行编辑修改，此课件供参考！ 部分内容来源于网络，如有侵权请与我联系删除！感谢你的观看！
C
A
P
B
精选课件ppt
O D
15
4、已知：如图， ⊙O的两条半径 OA⊥OB，C、D是弧AB的三等分点。
求证：CD＝AE＝BF。
A C
E
FD
O
B
精选课件ppt
16
弧、弦、弦心距之间的不等量关系
在同圆或等圆中，是不是弧越长，它所对的 弦越长？是不是弦越长，它所对的弧越长？
AB和CD是⊙O的两条弦，OM和ON分别是 AB和CD的弦心距，如果AB>CD，那么OM 和ON有什么关系？为什么？
E B
P
O
A
F 精选课件ppt
6
已知：如图，点O在∠EPF的平分线上，⊙O和 ∠ EPF的两边分别交于点A，B和C，D。
求证：AB＝CD
E
B
A
O
P
C
D
F
精选课件ppt
7
已知：如图， ⊙O的弦AB，CD相交于点P，
∠DPO=∠ BPO 。
A
求证：AB＝CD
C P
O
D
B 精选课件ppt
8
已知：如图， ⊙O的弦AB，CD相交于点P，过
圆心角、弧、弦、 弦心距之间的关系
精选课件ppt
1
圆的性质
圆是轴对称图形，每一条直径所在的直线都 是对称轴。
圆是以圆心为对称中心的中心对称图形。 圆还具有旋转不变性，即圆绕圆心旋转任意
一个角度α，都能与原来的图形重合。
精选课件ppt
2
圆心角：顶点在圆心的角。
（如：∠AOB）
A 弦心距：从圆心到弦的距离。