螺旋桨的定义及其效率计算
- 格式:doc
- 大小:28.00 KB
- 文档页数:3

螺旋桨是指靠桨叶在空气中旋转将发动机转动功率转化为推进力的装置或有两个或较多的叶与毂相连,叶的向后一面为螺旋面或近似于螺旋面的一种船用推进器。
螺旋桨分为很多种,应用也十分广泛,如飞机、轮船等。
1、古代的车轮,即欧洲所谓“桨轮”,配合蒸汽机,将原来桨轮的一列直叶板斜装于一个转毂上。
构成了螺旋桨的雏型;2、古代的风车,随风转动可以输出扭矩,反之,在水中,输入扭矩转动风车,水中风车就有可能推动船运动;3、在当时,已经使用了好几个世纪的阿基米德螺旋泵,它能在水平或垂直方向提水,螺旋式结构能打水这一事实,作为推进器是重要的启迪。
伟大的英国科学家虎克在1683年成功地采用了风力测速计的原理来计量水流量,于此同时,他提出了新的推进器——推进船舶,为船舶推进器作出了重大贡献。
船用螺旋桨的发展1752年,瑞士物理学家白努利第一次提出了螺旋桨比在它以前存在的各种推进器优越的报告,他设计了具有双导程螺旋的推进器,安装在船尾舵的前方。
1764年,瑞士数学家欧拉研究了能代替帆的其它推进器,如桨轮(明轮)。
喷水,也包括了螺旋桨。
潜水器和潜艇在水面下活动,传统的桨、帆无法应用,笨重庞大的明轮也难适应。
于是第一个手动螺旋桨,不是用在船上,而是作为潜水器的推进工具。
蒸汽机问世,为船舶推进器提供了新的良好动力,推进器顺应蒸汽机的发展,成为船舶推进的最新课题。
第一个实验动力驱动螺旋桨的是美国人斯蒂芬,他在1804年建造了一艘7.6米长的小船,用蒸汽机直接驱动,在哈得逊河上做第一次实验航行,实验中发现发动机不行,于是换上瓦特蒸汽机,实验航速是4节,最高航速曾达到8节。
斯蒂芬螺旋桨有4个风车式桨叶,它锻制而成,和普通风车比较它增加了叶片的径向宽度,为在实验中能选择螺距与转速的较好配合,桨叶做成螺距可以调节的结构。
在哈得逊河上两个星期的试验航行中,螺旋桨改变了几个螺距值,但是实验的结果都不理想,性能远不及明轮。
这次实验使他明白,在蒸汽机这样低速的条件下,明轮的优越性得到了充分发挥,它的推进效率高于螺旋桨是必然的结论。



螺旋桨公式一、工作原理可以把螺旋桨看成是一个一面旋转一面前进的机翼进行讨论。
流经桨叶各剖面的气流由沿旋转轴方向的前进速度和旋转产生的切线速度合成。
在螺旋桨半径r1和r2(r1<r2)两处各取极小一段,讨论桨叶上的气流情况。
V—轴向速度;n—螺旋桨转速;φ—气流角,即气流与螺旋桨旋转平面夹角;α—桨叶剖面迎角;β—桨叶角,即桨叶剖面弦线与旋转平面夹角。
显而易见β=α+φ。
空气流过桨叶各小段时产生气动力,阻力ΔD和升力ΔL,见图1—1—19,合成后总空气动力为ΔR。
ΔR沿飞行方向的分力为拉力ΔT,与旋螺桨旋转方向相反的力ΔP 阻止螺旋桨转动。
将整个桨叶上各小段的拉力和阻止旋转的力相加,形成该螺旋桨的拉力和阻止螺旋桨转动的力矩。
从以上两图还可以看到。
必须使螺旋桨各剖面在升阻比较大的迎角工作,才能获得较大的拉力,较小的阻力矩,也就是效率较高。
螺旋桨工作时。
轴向速度不随半径变化,而切线速度随半径变化。
因此在接近桨尖,半径较大处气流角较小,对应桨叶角也应较小。
而在接近桨根,半径较小处气流角较大,对应桨叶角也应较大。
螺旋桨的桨叶角从桨尖到桨根应按一定规律逐渐加大。
所以说螺旋桨是一个扭转了的机翼更为确切。
从图中还可以看到,气流角实际上反映前进速度和切线速度的比值。
对某个螺旋桨的某个剖面,剖面迎角随该比值变化而变化。
迎角变化,拉力和阻力矩也随之变化。
用进矩比“J”反映桨尖处气流角,J=V/nD。
式中D—螺旋桨直径。
理论和试验证明:螺旋桨的拉力(T),克服螺旋桨阻力矩所需的功率(P)和效率(η)可用下列公式计算:T=Ctρn2D4P=Cpρn3D5η=J·Ct/Cp式中:Ct—拉力系数;Cp—功率系数;ρ—空气密度;n—螺旋桨转速;D—螺旋桨直径。
其中Ct和Cp取决于螺旋桨的几何参数,对每个螺旋桨其值随J变化。
图1—1—21称为螺旋桨的特性曲线,它可通过理论计算或试验获得。
特性曲线给出该螺旋桨拉力系数、功率系数和效率随前进比变化关系。

螺旋桨设计计算公式桨叶的迎角只会影响升力的大小,不会前进。
直升机前进是靠螺旋桨的旋转面向前倾斜实现的,桨叶的迎角变化,指的只是桨叶本身绕横向的轴旋转。
就是对称的两只桨,成一条直线,以这个直线为轴旋转。
迎角增大,旋转阻力增大,如果转速不变的情况下,升力就会增大,直升机上升。
飞机螺旋桨由两个或者多个桨叶以及一个中轴组成,桨叶安装在中轴上。
飞机螺旋桨的每一个桨叶基本上是一个旋转翼。
由于他们的结构,螺旋桨叶类似机翼产生拉动或者推动飞机的力。
旋转螺旋桨叶的动力来自引擎。
引擎使得螺旋桨叶在空气中高速转动,螺旋桨把引擎的旋转动力转换成前向推力。
空气中飞机的移动产生和它的运动方向相反的阻力。
所以,飞机要飞行的话,就必须由力作用于飞机且等于阻力,而方向向前。
这个力称为推力。
典型螺旋桨叶的横截面如图3-26。
桨叶的横界面可以和机翼的横截面对比。
一种桨叶的表面是拱形的或者弯曲的,类似于飞机机翼的上表面,而其他表面类似机翼的下表面是平的。
弦线是一条划过前缘到后缘的假想线。
类似机翼,前缘是桨叶的厚的一侧,当螺旋桨旋转时前缘面对气流。
桨叶角一般用度来度量单位,是桨叶弦线和旋转平面的夹角,在沿桨叶特定长度的的特定点测量。
因为大多数螺旋桨有一个平的桨叶面,弦线通常从螺旋桨桨叶面开始划。
螺旋角和桨叶角不同,但是螺旋角很大程度上由桨叶角确定,这两个术语长交替使用。
一个角的变大或者减小也让另一个随之增加或者减小。
当为新飞机选定固定节距螺旋桨时,制造商通常会选择一个螺旋距使得能够有效的工作在预期的巡航速度。
然而,不幸运的是,每一个固定距螺旋桨必须妥协,因为他只能在给定的空速和转速组合才高效。
飞行时,飞行员是没这个能力去改变这个组合的。
当飞机在地面静止而引擎工作时,或者在起飞的开始阶段缓慢的移动时,螺旋桨效率是很低的,因为螺旋桨受阻止不能全速前进以达到它的最大效率。
这时,每一个螺旋桨叶以一定的迎角在空气中旋转,相对于旋转它所需要的功率大小来说产生的推力较少。



船用螺旋桨的功率计算功率(W)直径(D)螺距(P)转/分(N)功率(W)=(D/10)的4次方*(P/10)*(N/1000)的3次方*0.45速度(SP)km/h=(P/10)*(N/1000)*15.24静止推力(Th)g=(D/10)的3次方*(P/10)*(N/1000)的2次方*22船用螺旋桨的工作原理可以把螺旋桨看成是一个一面旋转一面前进的机翼进行讨论。
流经桨叶各剖面的气流由沿旋转轴方向的前进速度和旋转产生的切线速度合成。
在螺旋桨半径r1和r2(r1<r2)两处各取极小一段,讨论桨叶上的气流情况。
V—轴向速度;n—螺旋桨转速;φ—气流角,即气流与螺旋桨旋转平面夹角;α—桨叶剖面迎角;β—桨叶角,即桨叶剖面弦线与旋转平面夹角。
显而易见β=α+φ。
空气流过桨叶各小段时产生气动力,阻力ΔD和升力ΔL,合成后总空气动力为ΔR。
ΔR沿飞行方向的分力为拉力ΔT,与旋螺桨旋转方向相反的力ΔP 阻止螺旋桨转动。
将整个桨叶上各小段的拉力和阻止旋转的力相加,形成该螺旋桨的拉力和阻止螺旋桨转动的力矩。
从以上两图还可以看到。
必须使螺旋桨各剖面在升阻比较大的迎角工作,才能获得较大的拉力,较小的阻力矩,也就是效率较高。
螺旋桨工作时。
轴向速度不随半径变化,而切线速度随半径变化。
因此在接近桨尖,半径较大处气流角较小,对应桨叶角也应较小。
而在接近桨根,半径较小处气流角较大,对应桨叶角也应较大。
螺旋桨的桨叶角从桨尖到桨根应按一定规律逐渐加大。
所以说螺旋桨是一个扭转了的机翼更为确切。
从图中还可以看到,气流角实际上反映前进速度和切线速度的比值。
对某个螺旋桨的某个剖面,剖面迎角随该比值变化而变化。
迎角变化,拉力和阻力矩也随之变化。
用进矩比“J”反映桨尖处气流角,J=V/nD。
式中D—螺旋桨直径。
理论和试验证明:螺旋桨的拉力(T),克服螺旋桨阻力矩所需的功率(P)和效率(η)可用下列公式计算:T=Ctρn2D4 P=Cpρn3D5η=J·Ct/Cp 式中:Ct Cp—功率系数;ρ—空气密度;n—螺旋桨转速;D—螺旋桨直径。

螺旋桨的定义及其效率计算一、工作原理可以把螺旋桨看成是一个一面旋转一面前进的机翼进行讨论。
流经桨叶各剖面的气流由沿旋转轴方向的前进速度和旋转产生的切线速度合成。
在螺旋桨半径r1和r2(r1<r2)两处各取极小一段,讨论桨叶上的气流情况。
V—轴向速度;n—螺旋桨转速;φ—气流角,即气流与螺旋桨旋转平面夹角;α—桨叶剖面迎角;β—桨叶角,即桨叶剖面弦线与旋转平面夹角。
显而易见β=α+φ。
空气流过桨叶各小段时产生气动力,阻力ΔD和升力ΔL,见图1—1—19,合成后总空气动力为ΔR。
ΔR沿飞行方向的分力为拉力ΔT,与旋螺桨旋转方向相反的力ΔP 阻止螺旋桨转动。
将整个桨叶上各小段的拉力和阻止旋转的力相加,形成该螺旋桨的拉力和阻止螺旋桨转动的力矩。
从以上两图还可以看到。
必须使螺旋桨各剖面在升阻比较大的迎角工作,才能获得较大的拉力,较小的阻力矩,也就是效率较高。
螺旋桨工作时。
轴向速度不随半径变化,而切线速度随半径变化。
因此在接近桨尖,半径较大处气流角较小,对应桨叶角也应较小。
而在接近桨根,半径较小处气流角较大,对应桨叶角也应较大。
螺旋桨的桨叶角从桨尖到桨根应按一定规律逐渐加大。
所以说螺旋桨是一个扭转了的机翼更为确切。
从图中还可以看到,气流角实际上反映前进速度和切线速度的比值。
对某个螺旋桨的某个剖面,剖面迎角随该比值变化而变化。
迎角变化,拉力和阻力矩也随之变化。
用进矩比“J”反映桨尖处气流角,J=V/nD。
式中D—螺旋桨直径。
理论和试验证明:螺旋桨的拉力(T),克服螺旋桨阻力矩所需的功率(P)和效率(η)可用下列公式计算:T=Ctρn2D4P=Cpρn3D5η=J·Ct/Cp式中:Ct—拉力系数;Cp—功率系数;ρ—空气密度;n—螺旋桨转速;D—螺旋桨直径。
其中Ct和Cp取决于螺旋桨的几何参数,对每个螺旋桨其值随J变化。
图1—1—21称为螺旋桨的特性曲线,它可通过理论计算或试验获得。
特性曲线给出该螺旋桨拉力系数、功率系数和效率随前进比变化关系。
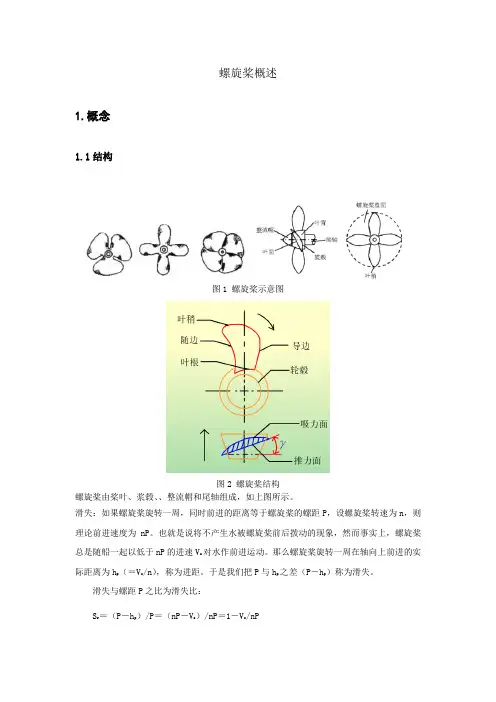
螺旋桨概述1.概念1.1结构图1 螺旋桨示意图图2 螺旋桨结构螺旋桨由桨叶、浆毂、、整流帽和尾轴组成,如上图所示。
滑失:如果螺旋桨旋转一周,同时前进的距离等于螺旋桨的螺距P,设螺旋桨转速为n,则理论前进速度为nP。
也就是说将不产生水被螺旋桨前后拨动的现象,然而事实上,螺旋桨总是随船一起以低于nP的进速V s对水作前进运动。
那么螺旋桨旋转一周在轴向上前进的实际距离为h p(=V s/n),称为进距。
于是我们把P与h p之差(P-h p)称为滑失。
滑失与螺距P之比为滑失比:S r=(P-h p)/P=(nP-V s)/nP=1-V s/nP式中V s/nP称为进距比。
从式中可以得出,当V s=nP时,S r=0。
即P=h,也就是螺旋桨将不产生对水前后拨动的现象,螺旋桨给水的推力为零。
因此我们可以得出结论:滑失越大,滑失比越高,则螺旋桨推水的速度也就越高,所得到的推力就越大。
1.2工作原理船用螺旋桨工作原理可以从两种不同的观点来解释,一种是动量的变化,另一种则是压力的变化。
在动量变化的观点上,简单地说,就是螺旋桨通过加速通过的水,造成水动量增加,产生反作用力而推动船舶。
由于动量是质量与速度的乘积,因此不同的质量配合上不同的速度变化,可以造成不同程度的动量变化。
另一方面,由压力变化的观点可以更清楚地说明螺旋桨作动的原理。
螺旋桨是由一群翼面构建而成,因此它的作动原理与机翼相似。
机翼是靠翼面的几何变化与入流的攻角,使流经翼面上下的流体有不同的速度,且由伯努利定律可知速度的不同会造成翼面上下表面压力的不同,因而产生升力。
而构成螺旋桨叶片的翼面,它的运动是由螺旋桨的前进与旋转所合成的。
若不考虑流体与表面间摩擦力的影响,翼面的升力在前进方向的分量就是螺旋桨的推力,而在旋转方向的分量就是船舶主机须克服的转矩力。
1.3推力和阻力以一片桨叶的截面为例:当船艇静止时,螺旋桨开始工作,把螺旋桨看成不动,则水流以攻角α流向桨叶,其速度为2πnr(n为转速;r为该截面半径)。

关于螺旋桨的一些知识.txt为什么我们在讲故事的时候总要加上从前?开了一夏的花,终落得粉身碎骨,却还笑着说意义。
关于螺旋桨的一些知识(转)螺旋桨 3d3v$\,f5W$h F3o一、工作原理:@,H"X3D,J7h"P!E;C可以把螺旋桨看成是一个一面旋转一面前进的机翼进行讨论。
流经桨叶各剖面的气流由沿旋转轴方向的前进速度和旋转产生的切线速度合成。
在螺旋桨半径r1和r2(r1<r2)两处各取极小一段,讨论桨叶上的气流情况。
V—轴向速度;n—螺旋桨转速;φ—气流角,即气流与螺旋桨旋转平面夹角;α—桨叶剖面迎角;β—桨叶角,即桨叶剖面弦线与旋转平面夹角。
显而易见β=α+φ。
+h)q4g'a {1Q9|8D空气流过桨叶各小段时产生气动力,阻力ΔD和升力ΔL,见图1—1—19,合成后总空气动力为ΔR。
ΔR沿飞行方向的分力为拉力ΔT,与旋螺桨旋转方向相反的力ΔP 阻止螺旋桨转动。
将整个桨叶上各小段的拉力和阻止旋转的力相加,形成该螺旋桨的拉力和阻止螺旋桨转动的力矩。
4A2_9?6^9A8P:| k从以上两图还可以看到。
必须使螺旋桨各剖面在升阻比较大的迎角工作,才能获得较大的拉力,较小的阻力矩,也就是效率较高。
螺旋桨工作时。
轴向速度不随半径变化,而切线速度随半径变化。
因此在接近桨尖,半径较大处气流角较小,对应桨叶角也应较小。
而在接近桨根,半径较小处气流角较大,对应桨叶角也应较大。
螺旋桨的桨叶角从桨尖到桨根应按一定规律逐渐加大。
所以说螺旋桨是一个扭转了的机翼更为确切。
&A4V7P8l;j3^7G/U9^2`/Y从图中还可以看到,气流角实际上反映前进速度和切线速度的比值。
对某个螺旋桨的某个剖面,剖面迎角随该比值变化而变化。
迎角变化,拉力和阻力矩也随之变化。
用进矩比“J”反映桨尖处气流角,J=V/nD。
式中D—螺旋桨直径。
理论和试验证明:螺旋桨的拉力(T),克服螺旋桨阻力矩所需的功率(P)和效率(η)可用下列公式计算:/L4p&M0[9l+X#p:w2P8]-dT=Ctρn2D4.J0].a%t)h;S(D,j0G*]P=Cpρn3D5 #I(l"z4},R1g0fη=J·Ct/Cp #w9A7D'j2L式中:Ct—拉力系数;Cp—功率系数;ρ—空气密度;n—螺旋桨转速;D—螺旋桨直径。
螺旋桨的定义及其效率计算一、工作原理可以把螺旋桨看成是一个一面旋转一面前进的机翼进行讨论。
流经桨叶各剖面的气流由沿旋转轴方向的前进速度和旋转产生的切线速度合成。
在螺旋桨半径r1和r2(r1<r2)两处各取极小一段,讨论桨叶上的气流情况。
V—轴向速度;n—螺旋桨转速;φ—气流角,即气流与螺旋桨旋转平面夹角;α—桨叶剖面迎角;β—桨叶角,即桨叶剖面弦线与旋转平面夹角。
显而易见β=α+φ。
空气流过桨叶各小段时产生气动力,阻力ΔD和升力ΔL,见图1—1—19,合成后总空气动力为ΔR。
ΔR沿飞行方向的分力为拉力ΔT,与旋螺桨旋转方向相反的力ΔP 阻止螺旋桨转动。
将整个桨叶上各小段的拉力和阻止旋转的力相加,形成该螺旋桨的拉力和阻止螺旋桨转动的力矩。
从以上两图还可以看到。
必须使螺旋桨各剖面在升阻比较大的迎角工作,才能获得较大的拉力,较小的阻力矩,也就是效率较高。
螺旋桨工作时。
轴向速度不随半径变化,而切线速度随半径变化。
因此在接近桨尖,半径较大处气流角较小,对应桨叶角也应较小。
而在接近桨根,半径较小处气流角较大,对应桨叶角也应较大。
螺旋桨的桨叶角从桨尖到桨根应按一定规律逐渐加大。
所以说螺旋桨是一个扭转了的机翼更为确切。
从图中还可以看到,气流角实际上反映前进速度和切线速度的比值。
对某个螺旋桨的某个剖面,剖面迎角随该比值变化而变化。
迎角变化,拉力和阻力矩也随之变化。
用进矩比“J”反映桨尖处气流角,J=V/nD。
式中D—螺旋桨直径。
理论和试验证明:螺旋桨的拉力(T),克服螺旋桨阻力矩所需的功率(P)和效率(η)可用下列公式计算:T=Ctρn2D4P=Cpρn3D5η=J·Ct/Cp式中:Ct—拉力系数;Cp—功率系数;ρ—空气密度;n—螺旋桨转速;D—螺旋桨直径。
其中Ct和Cp取决于螺旋桨的几何参数,对每个螺旋桨其值随J变化。
图1—1—21称为螺旋桨的特性曲线,它可通过理论计算或试验获得。
特性曲线给出该螺旋桨拉力系数、功率系数和效率随前进比变化关系。
动力学教程--螺旋桨动力学, 教程, 螺旋桨一、工作原理可以把螺旋桨看成是一个一面旋转一面前进的机翼进行讨论。
流经桨叶各剖面的气流由沿旋转轴方向的前进速度和旋转产生的切线速度合成。
在螺旋桨半径r1和r2(r1<r2)两处各取极小一段,讨论桨叶上的气流情况。
V—轴向速度;n—螺旋桨转速;φ—气流角,即气流与螺旋桨旋转平面夹角;α—桨叶剖面迎角;β—桨叶角,即桨叶剖面弦线与旋转平面夹角。
显而易见β=α+φ。
空气流过桨叶各小段时产生气动力,阻力ΔD和升力ΔL,合成后总空气动力为ΔR。
ΔR沿飞行方向的分力为拉力ΔT,与旋螺桨旋转方向相反的力ΔP 阻止螺旋桨转动。
将整个桨叶上各小段的拉力和阻止旋转的力相加,形成该螺旋桨的拉力和阻止螺旋桨转动的力矩。
从以上两图还可以看到。
必须使螺旋桨各剖面在升阻比较大的迎角工作,才能获得较大的拉力,较小的阻力矩,也就是效率较高。
螺旋桨工作时。
轴向速度不随半径变化,而切线速度随半径变化。
因此在接近桨尖,半径较大处气流角较小,对应桨叶角也应较小。
而在接近桨根,半径较小处气流角较大,对应桨叶角也应较大。
螺旋桨的桨叶角从桨尖到桨根应按一定规律逐渐加大。
所以说螺旋桨是一个扭转了的机翼更为确切。
从图中还可以看到,气流角实际上反映前进速度和切线速度的比值。
对某个螺旋桨的某个剖面,剖面迎角随该比值变化而变化。
迎角变化,拉力和阻力矩也随之变化。
用进矩比“J”反映桨尖处气流角,J=V/nD。
式中D—螺旋桨直径。
理论和试验证明:螺旋桨的拉力(T),克服螺旋桨阻力矩所需的功率(P)和效率(η)可用下列公式计算:T=Ctρn2D4P=Cpρn3D5η=J·Ct/Cp式中:Ct—拉力系数;Cp—功率系数;ρ—空气密度;n—螺旋桨转速;D—螺旋桨直径。
其中Ct和Cp取决于螺旋桨的几何参数,对每个螺旋桨其值随J变化。
图1—1—21称为螺旋桨的特性曲线,它可通过理论计算或试验获得。
特性曲线给出该螺旋桨拉力系数、功率系数和效率随前进比变化关系。
螺旋桨的理论基础习题答案螺旋桨的理论基础习题答案螺旋桨是一种常见的机械装置,被广泛应用于飞机、船舶等交通工具中。
它的作用是通过旋转产生推力或提供动力,使交通工具能够前进。
螺旋桨的理论基础涉及到一些物理学和工程学的知识,下面将针对一些常见的习题进行解答。
1. 什么是螺旋桨的工作原理?螺旋桨的工作原理是利用旋转产生的气流或水流来产生推力。
当螺旋桨旋转时,它会将周围的空气或水推向相反的方向,根据牛顿第三定律,推力会使交通工具朝着相反的方向移动。
2. 螺旋桨的推力与旋转速度、叶片角度有何关系?螺旋桨的推力与旋转速度和叶片角度有直接关系。
当旋转速度增加时,螺旋桨产生的推力也会增加。
叶片角度的变化也会影响推力,一般情况下,叶片角度越大,推力越大。
3. 如何计算螺旋桨的推力?螺旋桨的推力可以通过以下公式计算:推力 = 推力系数× 空气或水流的密度× 旋转速度的平方× 叶片面积其中,推力系数是一个与螺旋桨设计和工作条件相关的参数,可以通过实验或计算得到。
4. 螺旋桨的效率如何计算?螺旋桨的效率可以通过以下公式计算:效率 = 推力× 速度 / 功率其中,速度是交通工具前进的速度,功率是螺旋桨所需的能量。
5. 螺旋桨的设计有哪些要点?螺旋桨的设计要考虑多个因素,包括交通工具的速度、负载、工作环境等。
一般来说,螺旋桨的设计要追求高效率、低噪音和稳定性。
同时,螺旋桨的叶片形状、角度和数量也需要根据具体情况进行优化。
6. 如何改善螺旋桨的效率?要改善螺旋桨的效率,可以采取以下措施:- 优化叶片形状和角度,使其更适合流体流动,减小阻力;- 减小螺旋桨的重量,减少能量损耗;- 提高螺旋桨的旋转速度,增加推力;- 使用高效的材料和制造工艺,减少能量损耗。
7. 螺旋桨在船舶和飞机中有何不同?螺旋桨在船舶和飞机中的应用有一些不同之处。
在船舶中,螺旋桨主要用于推动船体前进,产生推力。
而在飞机中,螺旋桨除了产生推力外,还可以提供升力,使飞机能够在空中飞行。
旋螺桨作用力计算公式旋螺桨是一种常见的推进器,它通过旋转产生推进力,用于推动船只或飞机等交通工具。
在工程设计和运行过程中,了解旋螺桨的作用力计算公式是非常重要的。
本文将介绍旋螺桨作用力的计算公式及其相关知识。
旋螺桨作用力的计算公式可以通过流体力学的理论推导得到。
在流体力学中,旋螺桨的推进力可以通过螺旋桨的推进效率和流体动力学的基本原理来计算。
一般而言,旋螺桨的推进力可以通过以下公式来计算:F = ρ n^2 D^4 P。
其中,F表示旋螺桨的推进力,ρ表示流体的密度,n表示旋螺桨的转速,D表示旋螺桨的直径,P表示旋螺桨的推进效率。
从上述公式可以看出,旋螺桨的推进力与流体的密度、旋螺桨的转速、直径以及推进效率有关。
下面将分别介绍这些参数对旋螺桨推进力的影响。
首先是流体的密度。
流体的密度是旋螺桨推进力计算中的重要参数,它决定了流体对旋螺桨的阻力大小。
一般而言,流体的密度越大,旋螺桨所受到的阻力也越大,从而推进力也会增加。
其次是旋螺桨的转速。
旋螺桨的转速直接影响着推进力的大小。
一般而言,旋螺桨的转速越大,推进力也会越大。
因此,在设计旋螺桨时,需要根据具体的使用需求来确定旋螺桨的转速。
再次是旋螺桨的直径。
旋螺桨的直径也是影响推进力的重要参数。
一般而言,旋螺桨的直径越大,推进力也会越大。
因此,在设计旋螺桨时,需要根据船只或飞机的尺寸和使用需求来确定旋螺桨的直径。
最后是旋螺桨的推进效率。
旋螺桨的推进效率是指旋螺桨在推进过程中所产生的推进力与输入功率之比。
一般而言,推进效率越高,旋螺桨的推进力也会越大。
因此,在设计旋螺桨时,需要考虑如何提高旋螺桨的推进效率,以获得更大的推进力。
除了上述参数外,旋螺桨的推进力还受到流体的粘性、旋螺桨的形状和旋螺桨与船体或飞机的配合等因素的影响。
因此,在实际工程设计中,需要综合考虑这些因素,以确定旋螺桨的最佳设计参数。
在实际应用中,旋螺桨的推进力计算公式可以帮助工程师和设计师更好地设计和选择旋螺桨,以满足不同交通工具的推进需求。
螺旋桨的推进效率现在无论做什么事都要讲个效率,开会要讲开会的效率,能源也要讲个利用效率,你要是经常加班,老板会说你的效率太低了,这句话听着多伤心呐,讲效率的目的就是少投入,多产出,不给牛吃草,只让牛挤奶。
到处是讲效率的社会,我们也扒一扒螺旋桨工作时的效率吧。
船体效率ηH船体效率ηH 定义为有效(拖曳)功率PE= RT × V 与螺旋桨对水的推进功率PT = T × VA, 的比值,即:对于单桨船舶,船体效率ηH 通常介于1.1 - 1.4;船舶方形系数越大,效率值越高。
对于双桨船舶与传统的船体尾部线型,船体效率ηH 约为0.95-1.05,也是船舶方形系数越大,效率值越高。
但是,与单桨双艉船相比,双桨双艉船效率ηH 几乎不变。
螺旋桨敞水效率ηO螺旋桨敞水效率ηO 与敞水工况有关,即螺旋桨是在均匀的伴流场中工作,并且前方不存在船体。
螺旋桨效率主要取决于进速 VA、推力T、转速 n、直径 d 以及螺旋桨的设计情况,比如桨叶数、盘面比、螺距/直径比。
本章后面将进行探讨。
螺旋桨效率ηO 约为 0.35-0.75;螺旋桨进速 VA 越大,则效率值越高。
下图所示是船舶获得的螺旋桨效率ηO与进速VA 之间的关系,表示为无量纲量:其中 J 为螺旋桨进速系数螺旋桨相对旋转效率ηR水流流向船体后侧螺旋桨的实际速率非恒定,也非以正对流向螺旋桨盘面,而是属于一种旋流。
因此,与螺旋桨敞水工作相比,螺旋桨的效率受系数ηR 的影响,该系数称为螺旋桨相对旋转效率。
对于单桨船舶,效率ηR 一般约为1.0-1.07;换言之,水的旋流起到了有利的作用。
对于双桨常规船尾船舶,效率比ηR 通常较小,约为0.98;而对于双桨双艉船, 效率比ηR 几乎不变。
综合考虑 w和 t,ηR经常用于将船模水池实验结果调整到与理论一致。
船舶后侧工作的螺旋桨效率ηB是螺旋桨对水的推进功率 PT 与螺旋桨获得的功率 PD 的比值,即螺旋桨在船舶后侧工作时的效率ηB,定义为:推进效率ηD推进效率ηD 不能与螺旋桨敞水效率ηO混淆,它等于有效(拖曳)功率 PE 与螺旋桨所需功率 PD 的比值,即:可以看出,推进效率ηD 等于船体效率ηH、螺旋桨敞水效率ηO 与螺旋桨效率比ηR 三者的乘积,这些参数影响依次减弱。
螺旋桨的定义及其效率计算
一、工作原理
可以把螺旋桨看成是一个一面旋转一面前进的机翼进行讨论。
流经桨叶各剖面的气流由沿旋转轴方向的前进速度和旋转产生的切线速度合成。
在螺旋桨半径r1和r2(r1<r2)两处各取极小一段,讨论桨叶上的气流情况。
V—轴向速度;n—螺旋桨转速;φ—气流角,即气流与螺旋桨旋转平面夹角;α—桨叶剖面迎角;β—桨叶角,即桨叶剖面弦线与旋转平面夹角。
显而易见β=α+φ。
空气流过桨叶各小段时产生气动力,阻力ΔD和升力ΔL,见图1—1—19,合成后总空气动力为ΔR。
ΔR沿飞行方向的分力为拉力ΔT,与旋螺桨旋转方向相反的力ΔP 阻止螺旋桨转动。
将整个桨叶上各小段的拉力和阻止旋转的力相加,形成该螺旋桨的拉力和阻止螺旋桨转动的力矩。
从以上两图还可以看到。
必须使螺旋桨各剖面在升阻比较大的迎角工作,才能获得较大的拉力,较小的阻力矩,也就是效率较高。
螺旋桨工作时。
轴向速度不随半径变化,而切线速度随半径变化。
因此在接近桨尖,半径较大处气流角较小,对应桨叶角也应较小。
而在接近桨根,半径较小处气流角较大,对应桨叶角也应较大。
螺旋桨的桨叶角从桨尖到桨根应按一定规律逐渐加大。
所以说螺旋桨是一个扭转了的机翼更为确切。
从图中还可以看到,气流角实际上反映前进速度和切线速度的比值。
对某个螺旋桨的某个剖面,剖面迎角随该比值变化而变化。
迎角变化,拉力和阻力矩也随之变化。
用进矩比“J”反映桨尖处气流角,J=V/nD。
式中D—螺旋桨直径。
理论和试验证明:螺旋桨的拉力(T),克服螺旋桨阻力矩所需的功率(P)和效率(η)可用下列公式计算:
T=Ctρn2D4
P=Cpρn3D5
η=J·Ct/Cp
式中:Ct—拉力系数;Cp—功率系数;ρ—空气密度;n—螺旋桨转速;D—螺旋桨直径。
其中Ct和Cp取决于螺旋桨的几何参数,对每个螺旋桨其值随J变化。
图1—1—21称为螺旋桨的特性曲线,它可通过理论计算或试验获得。
特性曲线给出该螺旋桨拉力系数、功率系数和效率随前进比变化关系。
是设计选择螺旋桨和计算飞机性能的主要依据之一。
从图形和计算公式都可以看到,当前进比较小时,螺旋桨效率很低。
对飞行速度较低而发动机转速较高的轻型飞机极为不利。
例如:飞行速度为72千米/小时,发动转速为6500转/分时,η≈32%。
因此超轻型飞机必须使用减速器,降低螺旋桨的转速,提高进距比,提高螺旋桨的效率。
二、几何参数
直径(D):影响螺旋桨性能重要参数之一。
一般情况下,直径增大拉力随之增大,效率随之提高。
所以在结构允许的情况下尽量选直径较大的螺旋桨。
此外还要考虑螺旋桨桨尖气流速度不应过大(<0.7音速),否则可能出现激波,导致效率降低。
桨叶数目(B):可以认为螺旋桨的拉力系数和功率系数与桨叶数目成正比。
超轻型飞机一般采用结构简单的双叶桨。
只是在螺旋桨直径受到限制时,采用增加桨叶数目的方法使螺旋桨与发动机获得良好的配合。
实度(σ):桨叶面积与螺旋桨旋转面积(πR2)的比值。
它的影响与桨叶
数目的影响相似。
随实度增加拉力系数和功率系数增大。
桨叶角(β):桨叶角随半径变化,其变化规律是影响桨工作性能最主要的因素。
习惯上以70%直径处桨叶角值为该桨桨叶角的名称值。
螺距:它是桨叶角的另一种表示方法。
图1—1—22是各种意义的螺矩与桨叶角的关系。
几何螺距(H):桨叶剖面迎角为零时,桨叶旋转一周所前进的距离。
它反映了桨叶角的大小,更直接指出螺旋桨的工作特性。
桨叶各剖面的几何螺矩可能是不相等的。
习惯上以70%直径处的几何螺矩做名称值。
国外可按照直径和螺距订购螺旋桨。
如 64/34,表示该桨直径为60英寸,几何螺矩为34英寸。
实际螺距(Hg):桨叶旋转一周飞机所前进的距离。
可用Hg=v/n计算螺旋桨的实际螺矩值。
可按H=1.1~1.3Hg粗略估计该机所用螺旋桨几何螺矩的数值。
理论螺矩(HT):设计螺旋桨时必须考虑空气流过螺旋桨时速度增加,流过螺旋桨旋转平面的气流速度大于飞行速度。
因而螺旋桨相对空气而言所前进的距离一理论螺矩将大于实际螺矩。
三、螺旋桨拉力在飞行中的变化
1.桨叶迎角随转速的变化
在飞行速度不变的情况下,转速增加,则切向速度(U)增大,进距比减小桨叶迎角增大,螺旋桨拉力系数增大(图1—1—20所示)。
又由于拉力与转速平方成正比,所以增大油门时,可增大拉力。
2.桨叶迎角随飞行速度的变化:
在转速不变的情况下,飞行速度增大,进距比加大,桨叶迎角减小,螺旋桨拉力系数减小。
如图1—1—20所示,拉力随之降低。
当飞行速度等于零时,切向速度就是合速度,桨叶迎角等于桨叶角。
飞机在地面试车时,飞行速度(V)等于零,桨叶迎角最大,一些剖面由于迎角过大超过失速迎角气动性能变坏,因而螺旋桨产生的拉力不一定最大。
3.螺旋桨拉力曲线:
根据螺旋桨拉力随飞行速度增大而减小的规律,可绘出螺旋桨可用拉力曲线。
4.螺旋桨拉力随转速、飞行速度变化的综合情况:
在飞行中,加大油门后固定。
螺旋桨的拉力随转速和飞行速度的变化过程如下:
由于发动机输出功率增大,使螺旋桨转速(切向速度)迅速增加到一定值,螺旋桨拉力增加。
飞行速度增加,由于飞行速度增大,致使桨叶迎角又开始逐渐减小,拉力也随之逐渐降低,飞机阻力逐渐增大,从而速度的增加趋势也逐渐减慢。
当拉力降低到一定程度(即拉力等于阻力)后,飞机的速度则不再增加。
此时,飞行速度、转速、桨叶迎角及螺旋桨拉力都不变,飞机即保持在一个新的速度上飞行。
四、螺旋桨的自转:
当发动机空中停车后,螺旋桨会象风车一样继续沿着原来的方向旋转,这种现象,叫螺旋桨自转。
螺旋桨自转,不是发动机带动的,而是被桨叶的迎面气流“推着”转的。
它不但不能产生拉力,反而增加了飞机的阻力。
从图1—1—24中看出,螺旋桨发生自转时,由于形成了较大的负迎角。
桨叶的总空气动力方向及作用发生了质的变化。
它的一个分力(Q)与切向速度(U)的方向相同,成为推动桨叶自动旋转的动力,迫使桨叶沿原来方向续继旋转:另一个分力(-P)与速度方向相反,对飞行起着阻力作用。
一些超轻型飞机的发动机空中停车后由于飞行速度较小,产生自旋力矩不能克服螺旋桨的阻旋力矩时螺旋桨不会出现自转。
此时,桨叶阻力较大,飞机的升阻比(或称滑翔比)将大大降低。
五、螺旋桨的有效功率:
1.定义:螺旋桨产生拉力,拉着飞机前进,对飞机作功。
螺旋桨单位时间所作功,即为螺旋桨的有效功率。
公式: N桨=PV
式中: N桨—螺旋桨的有效功率;P—螺旋桨的拉力;V—飞行速度
2.螺旋桨有效功率随飞行速度的变化:
(1)地面试车时,飞机没有前进速度(V=0),拉力没有对飞机作功,故螺旋桨的有效功率为“零”。
(2)飞行速度增大时,从实际测得的螺旋桨有效功率曲线:
在OA速度范围内,螺旋桨的效功率随飞行速度的增大而增大;在大于该速度范围后螺旋桨有效功率则随飞行速度的增大而减小。
在OA速度范围内,当飞行速度增大时,拉力减小较慢,随速度的增大,螺旋桨有效功率逐渐提高。
当飞行速度增大到A时,螺旋桨的有效功率最大。
当飞行速度再增大时,由于拉力迅速减小,因此随着飞行速度的增加而螺旋桨有效功率反会降低。
螺旋桨是发动机带动旋转的,螺旋桨的作用是把发动机的功率转变为拉着飞机前进的有效功率。
螺旋桨有效功率与发动机输出功率之比,叫螺旋桨效率。
η=N桨/N有效。