下载文档原格式
口诀识别正方体展开图正方体有六个面，沿其中七条棱剪开可以得到一个由六个相同的正方形组成的平面图形，该图形虽然千姿百态，但六个正方形的排列是有一定规律的，并非胡乱拼接。
因此，在判断由六个正方形组成的图形中哪个是正方体展开图，哪个不是往往令人眼花缭乱。
为解决这个问题我们对正方体所有展开图用口诀归纳如下：首先，把六个正方形排列的行数和列数中较小的规定为行（当行数大于列数时，将图形旋转90°，列数便成了行数），则行数最小是2，最大是3。
行数二或三，个个边相连，不论何排列，去掉凹和田。
行二唯一见，每行三个现。
三行比大小，中间不能少。
“行数二或三”，指的是正方体展开图中的六个正方形要么排成两行，要么三行。
比如图1的行数是2，图2、图3的行数都是3，图4、图5的行数都是4，把它们旋转90°后行数就变成了3.“个个边相连”是指每个正方形都至少有一边与其他正方形是公共的。
否则它一定不是正方体展开图。
比如图3不是正方体展开图；“不论何排列，去掉凹和田”的意思是：不管六个正方形如何排列，一旦出现“凹”字型（如图6）或“田”字型（如图7）的，一定不是正方体展开图。
“行二唯一见，每行三个现”指的是排成两行的只有图1这种情形，每行都是3个正方形。
“三行比大小，中间不能少”说的是六个正方形排成三行的最多，而且排列方式五花八门，在这些排列中只要中间一行的个数不少于其他行的个数，再去掉图3、6、7这三种情形，那么它们都是正方体展开图。
显然，上述图1、图2、图4、图5都满足口诀条件，所以它们都是正方体展开图。
练习：下列由六个相同的正方形组成的图形中，哪些是正方体展开图？答案：（1）（3）（5）是，（2）（4）不是。
正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。
口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”“7”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。
口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。
口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。
口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。
口诀：中间没有面，三三连一线（1种摆法-33）。
正方体展开图11种图片顺口溜
11种图片顺口溜如下;
（一四一型：6种）顺口溜：中间四个一连串，两边各一随便放。
（二三一型：3种）顺口溜：二三紧连挪一个，三一相连一随便。
（二二二型：1种）顺口溜：两两相连各挪一。
（三三型1种）顺口溜：三个两排一对齐。
思路
空间形体的表面在平面上摊平后得到的图形，是画法几何研究的一项内容。
对于用板料制作的零件，除需要用多面正投影图表示零件的形状外，还要用展开图表示零件制作前板料的形状。
依据零件的多面正投影图绘制展开图，实质上就是求取表面的真实形状。
构成形体的表面可分为两类:平面、柱面和锥面等可以摊平的表面是可展曲面;球面和圆环面等不能摊平的表面是不可展曲面。
对于可展曲面，柱面用平行线法绘制其展开图，锥面用放射线法绘制其展开图。
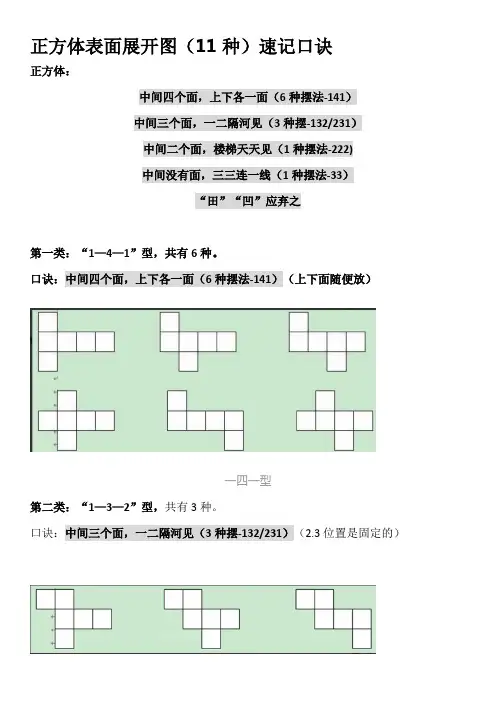
正方体表面展开图（11种）速记口诀
正方体：
中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，共有6种。
口诀：中间四个面，上下各一面（6种摆法-141）（上下面随便放）
一四一型
第二类：“1—3—2”型，共有3种。
口诀：中间三个面，一二隔河见（3种摆-132/231）（2.3位置是固定的）
二三一型第三类：“2—2—2”型，只有1种。
口诀：中间二个面，楼梯天天见（1种摆法-222)
第四类：“3—3”型，只有1种。
中间没有面，三三连一线（1种摆法-33）“田”“凹”应弃之（1种摆法-33）
三三型1种
（不能出现“7”字，“凹”字，“田”字形）如：。
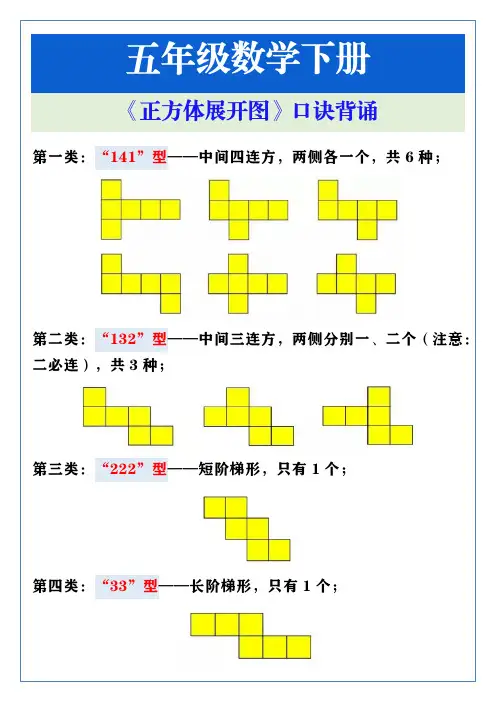
口诀：
一线不过四，田凹应弃之，相间"Z"端是对面，间二拐角邻面知.
一线不过四指的是一条线上的正方形不能超过四个，
田凹应弃之指的是含有“田”“凹”的图不是，
相间"Z"端是对面中的相间指的是一条线上中间隔着一个正方形的两个正方形合成正方体时是对面，"Z"端指的是图形中"Z"字形的两个端点的正方形合成正方体时是对面。
间二拐角邻面知中的间二指的是一条线上中间隔着两个正方形的两个正方形合成正方体时是邻面，拐角的两个正方形合成正方体时也是邻面。
巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形，经折叠能否围城正方体问题，是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手，现将确定正方体展开图的方法以口诀的方式总结出来，供大家参考：正方体盒巧展开，六个面儿七刀裁。
十四条边布周围，十一类图记分明：四方成线两相卫，六种图形巧组合；跃马失蹄四分开；两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下：将一个正方体盒的表面沿某些棱剪开，展开成平面图形，需剪7刀，故平面展开图中周围有14条边长共有十一种展开图：一、四方成线两相卫，六种图形巧组合（1）（2）（3）（4）（5）（6）以上六种展开图可归结为四方连线，即，另外两个小方块在四个方块的上下两侧，共六种情况。
二、跃马失蹄四分开（1）（2）（3）（4）以上四种情况可归结为五个小方块组成“三二相连”的基本图形（如图），另外一个小方块的位置有四种情况，即图中四个小方块中的任意一个，这一图形有点像失蹄的马，故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组，两两错开，像阶梯一样，故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法，也是确定展开图中的对面的一种方法。
如果出现三个相连，则1号面与3号面是对面，中间隔了一个2号面，并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”（1） （2） （3）这里介绍的是一种排除法。
如果图中出现象图（1）中的“7”形结构的图形不可能是正方体展开图的，因为图中1号面与3号面是对面，3号面又与5号面是对面，出现矛盾。
如果图中出现象图（2）中的“田”形结构的图形不可能是正方体展开图的，因为同一顶点处不可能出现四个面的。
如果图中出现象图（3）中的“凹”形结构的图形不可能是正方体展开图的，因为如果把该图形折叠起来将有两个面重合。
现举例说明：例1．（2004海口市实验区）下面的平面图形中，是正方体的平面展开图的是（ ）解析：本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
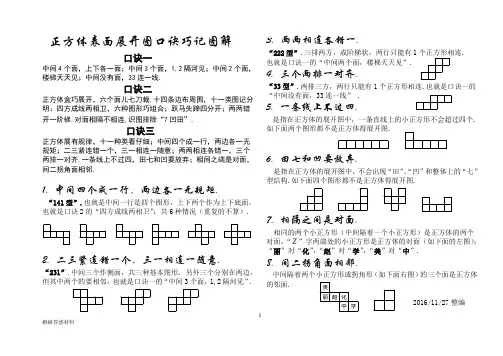
1解疑答惑材料正方体表面展开图口诀巧记图解口诀一中间4个面，上下各一面；中间3个面，1,2隔河见；中间2个面，楼梯天天见；中间没有面，33连一线.口诀二正方体盒巧展开，六个面儿七刀裁.十四条边布周围，十一类图记分明：四方成线两相卫，六种图形巧组合；跃马失蹄四分开；两两错开一阶梯.对面相隔不相连,识图排除“7凹田”.口诀三正方体展有规律，十一种类看仔细；中间四个成一行，两边各一无规矩；二三紧连错一个，三一相连一随意；两两相连各错一，三个两排一对齐.一条线上不过四，田七和凹要放弃；相间之端是对面，间二拐角面相邻.1. 中间四个成一行，两边各一无规矩.“141型”.也就是中间一行是四个图形，上下两个作为上下底面，也就是口诀2的“四方成线两相卫”；共6种情况（重复的不算）.2. 二三紧连错一个，三一相连一随意.“231”.中间三个作侧面，共三种基本图形. 另外三个分别在两边，但其中两个的要相邻；也就是口诀一的“中间3个面，1,2隔河见”. 3. 两两相连各错一.“222型”.三排两方，成阶梯状，两行只能有1. 也就是口诀一的“中间两个面，楼梯天天见”.4. 三个两排一对齐.“33型”.两排三方，两行只能有1个正方形相连.也就是口诀一的“中间没有面，33连一线” .5. 一条线上不过四.是指在正方体的展开图中，一条直线上的小正方形不会超过四个.如下面两个图形都不是正方体得展开图.6. 田七和凹要放弃.是指在正方体的展开图中，不会出现“田”、“凹”和整体上的“七”型结构.如下面四个图形都不是正方体得展开图.7. 相隔之间是对面.相同的两个小正方形（中间隔着一个小正方形）是正方体的两个对面，“Z ”字两端处的小正方形是正方体的对面（如下面的左图）：“丽”对“化”，“赵”对“学”，“美”对“中”.8. 间二拐角面相邻.中间隔着两个小正方形或拐角形（如下面右图）的三个面是正方体的邻面.2016/11/27整编。
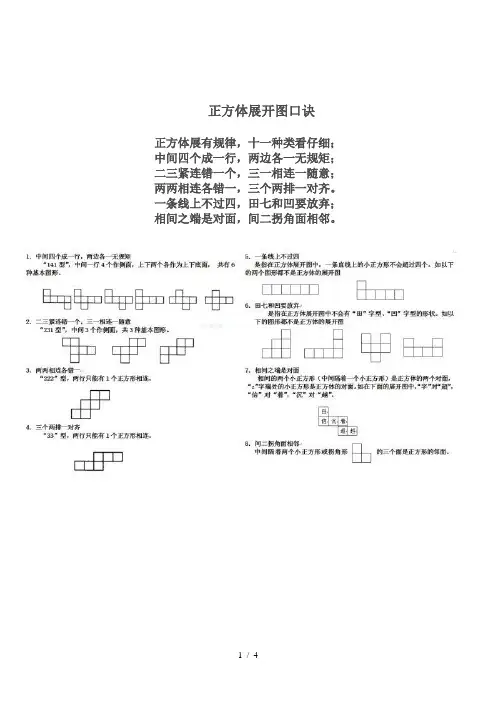
正方体展开图口诀正方体展有规律，十一种类看仔细；中间四个成一行，两边各一无规矩；二三紧连错一个，三一相连一随意；两两相连各错一，三个两排一对齐。
一条线上不过四，田七和凹要放弃；相间之端是对面，间二拐角面相邻。
巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形，经折叠能否围城正方体问题，是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手，现将确定正方体展开图的方法以口诀的方式总结出来，供大家参考：正方体盒巧展开，六个面儿七刀裁。
十四条边布周围，十一类图记分明：四方成线两相卫，六种图形巧组合；跃马失蹄四分开；两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下：将一个正方体盒的表面沿某些棱剪开，展开成平面图形，需剪7刀，故平面展开图中周围有14条边长共有十一种展开图：一、四方成线两相卫，六种图形巧组合（1）（2）（3）（4）（5）（6）以上六种展开图可归结为四方连线，即，另外两个小方块在四个方块的上下两侧，共六种情况。
二、跃马失蹄四分开（1）（2）（3）（4）以上四种情况可归结为五个小方块组成“三二相连”的基本图形（如图），另外一个小方块的位置有四种情况，即图中四个小方块中的任意一个，这一图形有点像失蹄的马，故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组，两两错开，像阶梯一样，故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法，也是确定展开图中的对面的一种方法。
如果出现三个相连，则1号面与3号面是对面，中间隔了一个2号面，并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”12312345（1）（2）（3）这里介绍的是一种排除法。
如果图中出现象图（1）中的“7”形结构的图形不可能是正方体展开图的，因为图中1号面与3号面是对面，3号面又与5号面是对面，出现矛盾。
如果图中出现象图（2）中的“田”形结构的图形不可能是正方体展开图的，因为同一顶点处不可能出现四个面的。
正方体展开图口诀
正方体盒巧展开，六个面儿七刀裁；
十四条边布周围，十一类图记分明。
中间四个成一行，两边各一无规矩；
二三紧连错一个，三一相连一随意；
两两相连各错一，三个两排一对齐。
一条线上不过四，田七和凹要放弃；
相间之端是对面，间二拐角面相邻。
1.中间四个成一行，两边各一无规矩；
“141型”，中间一行4个作侧面，上下两个各为上下底面，共6种基本图形。
2.二三紧连错一个，三一相连一随意；
“231型”，中间3个作侧面，共3种基本图形。
3.两两相连各错一，三个两排一对齐。
“222型”，两行只能有1个正方形相连。
“33型”，两行只能有1个正方形相连。
4.一条线上不过四，田七和凹要放弃；
正方体展开图中，一条直线上的小正方形不会超过4个。
（×）（×）
正方体展开图中不会有“田”字型、“凹”字型的形状。
如下都不是正方体的展
开图。
（×）
5.相间之端是对面，间二拐角面相邻。
相间的两个小正方形（中间隔着一个小正方形）是正方体的两个对面，“z”字端处的小正方形是正方体的对面。
如右图，“字”对“超”，“信”对“着”，“沉”对“越”
中间隔着两个小正方形或拐角型的三个面是正方形的邻面。
