中职数学第三章函数复习

列表法和解析法表示购买4支以内的签字笔时，应付款与
签字笔支数之间的函数．
解 设表示购买签字笔的支数，表示应付款数（元），则
∈ 1,2,3,4 ．
（1）列表法表示见表
（2）解析法表示为： = 6.5， ∈ 1,2,3,4 ．
情境
导入
探索
新知
例题
辨析
巩固
练习
归纳
总结
布置
作业
例2 现阶段,我国很多城市普遍采用“阶梯水价”的办法计量水费，发
（1） = 2 + 5与 = ( + 5)；
（2） = − 1与 =
（3）() =
2 −4
与()
+2
−1

；
= − 2．
情境
导入
探索
新知
例题
辨析
巩固
练习
归纳
总结
布置
作业
4．设函数 = 2 + 2 ，x∈R． 求 2 ， −2 ，
解 （1）虽然函数 = + 1与函数 = + 1中表示
自变量的字母不同，但它们的定义域和对应法则都是相同
的，所以它们表示的是同一个函数；
（2）因为函数 = 的定义域为 ，函数 =
2

的定义域为{x|x≠0}，它们的定义域不同，因此它们表示的
不是同一个函数．
2
．
；
；
．
情境
导入
探索
新知
例题
辨析
巩固
练习
归纳
总结
布置
作业
2， − 1 ≤ ≤ 0，
4．已知函数() = ൞ + 2， 0 < < 2， 则

第三章 函数第1节 函数的概念及其表示法一、函数的定义：函数的两个要素：定义域与对应法则。

【习题】1.指出下列各函数中，哪个与函数y x =是同一个函数：（1）xx y 2=（2）2x y =（3）()2x y =（4）t s =2.判定下列各组函数是否为同一个函数：（1）()x x f =与()33x x f =（2）()1+=x x f 与()112--=x x x f二、函数的定义域：确定定义域，需要考虑以下几个方面：如果解析式1.为整式，定义域为R.2.有分式，分母不能为0.3.有偶次根式，被开方数≥0.4.有对数，对数的底数大于0且不等于1，对数的真数>05.有几种情况同时存在，使它们同时成立，取交集。

6.考虑实际意义。

【习题】求下列各函数的定义域：1.（1）2)+=x x f （ （2）()32+-=x x x f 2.（1）()4x 2x f +=（2）()541x f -=x （3）236)(2+-=x x x f 3.（1）()5x 6-x x f 2+= (2)5-x 4)(=x g (3)65)(2+-=x x x f 4.(1）()42log 3+=x y (2)()x y 35log 3-= (3)()43log 2-=x y5.(1)541)(-=x x h （2）131)(+++-=x x x u (3)14)(2--=x x x f (4)1log 131-=x y 三、函数的值（域）【习题】1.()32x f -=x ，求()2f 2.()121-+=t t t g ，求()0g ，()1-g ，()1+a g 3. 设()213x f x -=，求()0f ，()2f ，()5f -，()f b ． 4.已知函数()14+=x x f ，{}4,3,2,1,0∈x ，求这个函数的值域。

四、函数的表示法1.解析法：等式。

2.列表法：表格。

3.图像法：图像。

第三章 函数第三章 第一课时 函数的概念【基础知识·一定要看】1．函数的概念设A 、B 是非空的数集，如果按照某个确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B 中都有__________的数 f x 和它对应，那么就称:f A B 为从集合A 到集合B 的一个函数．记作： y f x ，x A ．其中，x 叫做自变量，x 的取值范围A 叫做函数的定义域；与x 的值相对应的y 值叫做函数值，函数值的集合 {|}f x x A 叫做函数的值域. 2．求函数定义域的常用方法： （1）分母不为零；（2）偶次根式，则被开方数大于或等于零； （3）0的0次没有意义；（4）对数的真数大于零；（还没学）3．相同函数：个函数相等当且仅当它们的定义域和对应关系完全—致，而与表示自变量和函数值的字母无关．4．分段函数：如果函数y ＝f (x )，x ∈A ，根据自变量x 在A 中不同的取值范围，有着不同的对应关系，则称这样的函数为分段函数． 一、选择题1．在下面四个图中，可表示函数 y f x 的图象的可能是（ ）A． B． C． D．2．函数1()f x x的定义域是（ ） A．[2,0)(0,)B．[2,) C．RD．(,0)(0,)3．下列每组中的两个函数是同一函数的是（ ）A．1y 与0y x ; B．y y x ;C．y x 与2y;D．y x 与y4． 23,12,1x x f x x x ，则(2)f 等于（ ）A．-2 B．0C．1D．65．函数 2112f x x x， 0,4x 的值域（ ）A． 0,4 B． 1,5 C． 1,4D．1,526．已知 2146f x x ，则 5f 的值为（ ） A．26B．20C．18D．167．已知函数 2,32,3x x f x x x .则 3f f （ ）A．1 B．4 C．9 D．16二、填空题8．函数()1f x 的定义域为 . 9．若 234f x x Bx ，且 112f ，则B = . 10．已知函数()y f x 的表达式4()1f x x，若()2f a ，则实数 a . 11．二次函数 22f x x x ， 1,1x ，则函数 f x 在此区间上的值域为 . 三、解答题12．已知函数 1f x ax x过点（1，5），求a 的值.第三章 第二课时 函数的表示方法【基础知识·一定要看】1．函数的三种表示方法：①待定系数法：若已知f （x ）的解析式的类型，设出它的一般形式，根据特殊值确定相关的系数即可.②换元法：设t ＝g （x ），解出x ，代入f （g （x ）），求f （t ）的解析式即可. 3．常见的几种基本初等函数①正比例函数(0)y kx k ②一次函数(0)y kx b k ③反比例函数(0)ky k x④二次函数2(0)y ax bx c a 一、选择题1．已知(21)44f x x ，则(1)f 的值为（ ） A．2B．4C．6D．82．函数 y f x 的图象如图所示，则 9f （ ） A．5 B．4C．3D．23．已知 212f x x x ，则 f x （ ） A．2xB．21xC．21xD．22x4．已知 f x 是反比例函数，且(3)1f ，则 f x 的解析式为（ ） A． 3f x xB． 3f x xC． 3f x xD． 3f x x5．若函数 f x 和 g x 分别由下表给出： 则 1g f （ ） A．4 B．3C．2D．16．已知 32f x x ，则 21f x 等于（ ） A．32xB．61x C．21xD．65x7．已知()f x 是一次函数，且(1)35f x x ，则()f x 的解析式为（ ） A．()32f x xB．()32f x xC．()23f x xD．()23f x x二、填空题8．已知 22143f x x ，则 f x .9．已知函数 f x 对于任意的x 都有 212f x x f x ，则 f x . 10．已知等腰三角形的周长为18，底边长为x ，腰长为y ，则y 关于x 的函数关系式为 . 三、解答题11．已知函数 224f x x x ． （1）求 0f ； （2）求 f x 的解析式．第三章 第三课时 函数的性质【基础知识·一定要看】1．函数的单调性 ①单调函数的定义 自左向右看图象是上升的自左向右看图象是下降的②证明函数单调性的步骤第一步：取值．设12x x ，是()f x 定义域内一个区间上的任意两个自变量，且12x x ； 第二步：变形．作差变形（变形方法：因式分解、配方、有理化等）或作商变形； 第三步：定号．判断差的正负或商与1的大小关系； 第四步：得出结论． 2．函数的奇偶性 ①函数奇偶性的概念偶函数：若对于定义域内的任意一个x ，都有 f x f x ，那么 f x 称为偶函数． 奇函数：若对于定义域内的任意一个x ，都有 f x f x ，那么 f x 称为奇函数． ②奇偶函数的图象与性质偶函数：函数()f x 是偶函数 函数()f x 的图象关于y 轴对称； 奇函数：函数()f x 是奇函数 函数()f x 的图象关于原点中心对称；若奇函数()y f x 在0x 处有意义，则有(0)0f .③用定义判断函数奇偶性的步骤第一步：求函数()f x 的定义域，判断函数的定义域是否_______________，若不关于原点对称，则该函数既不是奇函数，也不是偶函数，若关于原点对称，则进行下一步；第二步：求()f x ，若 f x f x ，则()f x 是奇函数；若()f x =()f x ，则()f x 是偶函数；若()()f x f x ，则()f x 既不是奇函数，也不是偶函数；若()()f x f x 且 f x f x ，则()f x 既是奇函数，又是偶函数.1．若函数 1y a x b ，x R 在其定义域上是增函数，则（ ） A．1aB．1aC．0bD．0b2．函数 f x 在R 上是减函数，则有（ ） A． 25f fB． 25f fC． 25f fD． 25f f3．下列函数中，既是偶函数又在 0, 上单调递增的函数是（ ） A．y xB．1y xC．21y xD．1y x4．若偶函数 f x 在 ,1 上是减函数，则（ ） A． 2.513f f f B． 1 2.53f f f C． 3 2.51f f fD． 31 2.5f f f5．函数 f x 是定义在 0, 上的增函数，则满足 1213f x f的x 的取值范围是（ ） A．12,33B．12,33C．12,23D．12,236．函数22y x x 单调减区间是（ ） A．1,2B． 1,C．1,2D． ,【填空】7．已知 f x 是偶函数， 12f ，则 11f f .8．函数()y f x 是定义在R 上的增函数，且 29f m f m ，则实数m 的取值范围是 .9．函数()y f x 是定义在R 上的奇函数，当0x 时，3()f x x x ，则(2)f .10．已知 y f x 在定义域 0,1上是减函数，且 121f a f a ，则实数a 的取值范围 .11．已知函数2()()2f x x m .（1）若函数()f x 的图象过点（2，2），求函数y ()f x 的单调递增区间； （2）若函数()f x 是偶函数，求m 值.12．已知函数 1f x x x（1）判断 f x 的奇偶性并说明理由； （2）判断 f x 在 0,1上的单调性并加以证明.第三章 第四课时 函数的应用一、选择题1．据调查，某存车处（只存放自行车和电动车）在某天的存车量为400辆次，其中电动车存车费是每辆一次2元，自行车存车费是每辆一次1元．若该天自行车存车量为x 辆次，存车总收入为y 元，则y 关于x 的函数关系式是（ ） A． 4000400y x x B． 8000400y x x C． 4000400y x xD． 8000400y x x2．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P （千帕）是气球体积V （立方米）的反比例函数，其图像如图所示，则这个函数的解析式为（ ）A．69P VB．96P VC．69P VD．96P V3．某物体一天中的温度T 是时间t 的函数：3()360T t t t ，时间的单位是小时，温度的单位是C ，0 t 表示中午12时，其后取值为正，其前取值为负，则上午8时的温度为（ ） A．18CB．8CC．0CD．4C二、填空题4．若某一品种的练习册每本2.5元，则购买x 本的费用y 与x 的函数关系是 . 5．某社区超市的某种商品的日利润y （单位：元）与该商品的当日售价x （单位：元）之间的关系为21221025x y x ，那么该商品的日利润最大时，当日售价为 元.三、解答题6．某出版社出版一种适合中学生阅读的科普读物，若该读物首次出版印刷的印数不少于5000册时，投入的成本与印数间的相应数据如下：（1）经过对上表中数据的探究，发现这种读物的投入成本 （元）是印数 （册）的一次函数，求这个一次函数的解析式（不要求写出的取值范围）； （2）如果出版社投入成本48000元，那么能印该读物多少册？x x7．制作一种产品，需先将材料加热达到60℃后，再进行操作，设该材料温度为y (℃)，从加热开始计算的时间为 min x ．据了解，设该材料加热时，温度y 与时间x 成一次函数关系；停止加热进行操作时，温度y 与时间x 成反比例关系(如图)．已知该材料在操作加工前的温度为15℃，加热5min 后温度达到60℃．(1)分别求出将材料加热和停止加热进行操作时，y 与x 的函数关系式；(2)根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？。

第三章 函数
考点：函数单调性
【例5】 下列函数中，满足“在其定义域上任取x1，x2，若x1<
x2，则f(x1)>f(x2)”的函数是( B
A．y＝ 3 B．y＝3－ x
x
2
)
C．y＝
1 2
x
D．y＝lnx
【思路点拨】 考虑单调性的定义．
【答案详解】 A在其定义域内不单调，C、D均为增函数，故 选B.
数m的取值范围．
解：①当m＝0时，y＝ 8，定义域为R.
②当m≠0时，要使mx2－6mx＋m＋8≥0恒成立，
则只需 m 0,
综上得m∈=[306，m21]. 4mm 8 0,
解得0<m≤1，
第17页，共34页
第三章 函数
8．已知函数y1＝|x|，y2＝ 1 x 的4 图象如图所示，则当y1>y2 时，x的取值范围是( A ) 3 3
1．理解函数的概念，会求一些常见函数的定义域，会求 简单函数的值域，会作一些简单函数的图象．
2．理解函数的单调性的概念，了解增函数、减函数的图 象特征．
第三章 函数
考点：函数的概念和表示
第三章 函数
【练1】函数f(x)＝3x－1，x∈{－1，0，1，2，3}的图象是( D )
A．直线
B．射线 C．线段 D．离散的点
A．(－∞，－1)∪(，1)∪(2，＋∞)
D．(－1，2)
第8题图
【提示】 数形结合．
第18页，共34页
第三章 函数
笛卡尔坐标系
2
某地上空一只小小的蝴蝶扇动翅膀 而扰动了空气，长时间后可能导致遥远 的彼地发生一场暴风雨。
“蝴蝶效应”是关于混沌学的一个
比喻，不起眼的一个小动作却能引起 一连串的巨大反应。

底数≠0.
5
3 函数式含偶次根式时,
被开方数≥0.
4
函数式含对数式loga x 时,
真数 x > 0, 底数 a > 0 且≠1.
题型四：求函数值
代入法
练4 若函数 f (x) x2 3 （P29 T5）
则 f (1) _____，f (2) _____，f (2x 1) _____.
题型五：求函数的值域
②列表法 x/支 1 2 3 4 5 y/元 0.8 1.6 2.4 3.2 4.0
考点四 函数的表示方法 ③图象法 y = 0.8x , x ∈{1,2,3,4,5} 五个点
y = 0.8x , x ∈[ 1 , 5 ] 线段
y = 0.8x , x ∈[ 1 , +∞ ) 射线
y = 0.8x , x ∈ R
练2 下列函数中哪个与函数 y x相等？
（1）y
x
2
；
y x,
x 0,
（2）y 3 x3 ； y x, x R
（3）y x2 ； y x , x R
（4） y x2 . y x, x x x 0 x
题型三：求函数的定义域
练3 求下列函数的定义域：（P28例2）
（1）f (x) 1 x 2x 1
直线
思考考：点（四1）函分段数函的数表是几示个方函法数吗？ 是一个函数
【例】（2）分段函数的定义域是什么？ 自变量各个取值范围的并集
（2）函数的图像如下.
解 （1）函数的解析式为
国内跨省市之间邮寄信函,每封信函的质量m（克）
和对应的邮资M（元）如表3-4所示:
分段函数

题型六：求分段函数的函数值
练6
[0,4] [ 4 , 14 ]

第23课时 章末复习与小结（一）【目标导航】1.通过整理全章知识的过程，掌握本章的基本知识，基本的数学思想及方法；2.掌握本章的基本的数学题型，解题思路，熟练解题技巧。

【要点整理】 （一）函数的概念1、概念： 在某一个变化过程中有两个变量x 和y ，设变量x 的取值范围为数集D ，如果对于D 内的 值，按照某个对应法则f ，y 都有 值与它 ，那么，把x 叫做 ，把y 叫做x 的 ．2.表示： 将上述函数记作 ．变量x 叫做自变量，数集D 叫做函数的 ．3.函数值的概念： 函数值．记作 .4.函数的定义域： 。

5.定义域的求法：（1） ；（2） ；（3） ；（4） ；（5） ；（6） ；6.函数的值域：函数值的集合(){}|,y y f x x D =∈叫做函数的值域．7.基本初等函数的值域的求法： 。

8. 同一函数的理解：（1）函数的三要素：1） ；2） ；3） 。

2）什么是同一函数： 。

（二）函数的表示 1. 函数的三种表示：（1） ；（2） ；（3） 。

2. “描点法”画图的基本步骤：（1） ；（2） ；（3） 。

3.三种表示法的优缺点比较：（1）常见解析式的设法：一次函数： ；正比例函数 ；反比例函数： ；二次函数： 。

（2）待定系数法求解析式的一般步骤：1）设； 。

2）列； 。

3）解； 。

4）写； 。

（3）简单的抽象函数的解析式的求法：① ② 。

（三）函数的性质 1.单调性：（1）单调增函数的定义： 在区间(),a b 内，随着 的增加，函数值 ，图像呈 趋势．即对于 的()12,,x x a b ∈，当 时，都有 成立．这时把函数()f x 叫做区间(),a b 内的 ，区间(),a b 叫做函数()f x 的 ．此时，区间(,)a b 叫做函数()f x 的 。

（2）单调减函数的定义：在区间(),a b 内，随着 的增加，函数值 ，图像呈 趋势．即对于 的()12,,x x a b ∈，当 时，都有 成立．这时把函数()f x 叫做区间(),a b 内的 ，区间(),a b 叫做函数()f x 的 ． （2）单调性的概念：①单调性： 。

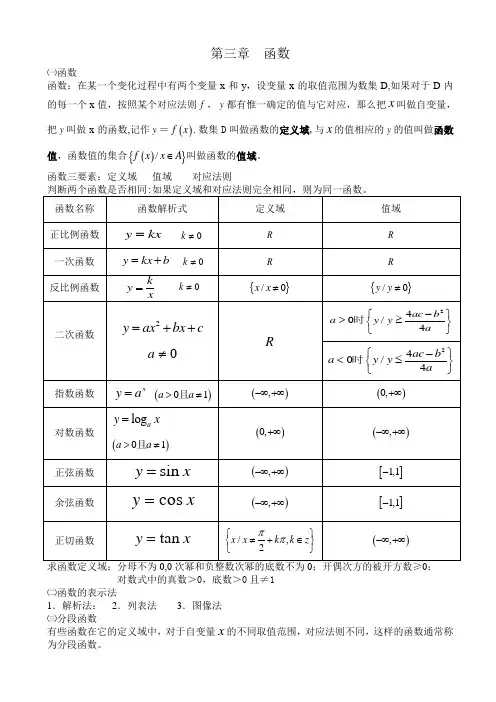
第三章 函数㈠函数函数：在某一个变化过程中有两个变量x 和y ，设变量x 的取值范围为数集D,如果对于D 内的每一个x 值，按照某个对应法则f ，y 都有惟一确定的值与它对应，那么把x 叫做自变量，把y 叫做x 的函数,记作y ＝()f x .数集D 叫做函数的定义域,与x 的值相应的y 的值叫做函数值，函数值的集合(){}/f x x A ∈叫做函数的值域。

函数三要素：定义域 值域 对应法则对数式中的真数＞0，底数＞0且≠1㈡函数的表示法1．解析法： 2．列表法 3．图像法 ㈢分段函数有些函数在它的定义域中，对于自变量x 的不同取值范围，对应法则不同，这样的函数通常称为分段函数。

㈣二次函数2y ax bx c=++(0a≠)顶点坐标24,24b ac ba a⎛⎫--⎪⎝⎭，对称轴2bxa=-，最值244ac ba-与y轴的交点：（0, c）判别式△＝b2-4ac当△＞0时，函数图像与X轴有两个交点;当△=0时，函数图像与X轴有一个交点；当△＜0时，函数图像与X轴没有交点㈥函数的单调性和奇偶性1．增函数：对于给定区间上的函数()f x ，如果对于这个区间上的任意两个12,x x ， 当12x x <时，都有()()12f x f x <，那么就说()f x 在这个区间上是增函数（或单调递增函数）。

2．减函数：对于给定区间上的函数()f x ，如果对于这个区间上的任意两个12,x x ，当12x x <时，都有()()12f x f x >，那么就说()f x 在这个区间上是减函数（或单调递减函数）。

对于函数()y f x =在某个区间上单调递增或单调递减的性质，叫做()f x 在这个区间上的单调性。

这个区间叫做()f x 的单调区间。

图像性质：增函数图像沿x 轴正方向，即从左向右逐渐上升的。

减函数图像沿x 轴正方向，即从左向右逐渐下降的。

3．奇函数：如果函数()y f x =对其定义域D 内任意一个x 值，且x D -∈，都有()()f x f x -=-，那么函数()f x 就叫奇函数。

A．是增函数
B．是减函数
C．可能增函数也可能减函数
（2）函数的奇偶性： ①对于函数f(x) ，其定义域关于原点对称：
②若_f(_-_x_)_=_-__f(_x_)，则 f(x)为奇函数； 若__f(_-_x_)=__f_(_x_) ，则f(x) 为偶函数. ③奇函数的图像关于__原__点______对称，偶函数的图像关于___y_轴_____对称. ④奇函数在对称区间的增减性相同 ；偶函数在对称区间的增减性相反 .x fx m 3x 1 3x 1
m 3x 1 3x 1
m 13x
3x 1 0
1 0 m 1
例3 已知函数 y x2 4(a 2)x 4 在,6 上是增函数，试确定
实数a的取值范围.
答案：由对称轴
x
4a 2 2 1
6
a
5
例4 定义在(－1, 1)上的奇函数f (x)是减函数，解关于a的不等式： f (1―a)＋f (1―a²)<0.
（二）课堂探究
1.探究问题： 【探究1】我们有过许多对“美”的感受，“对称美”就大量存在于我们的生活 中.观察以下图形，分析以下有什么对称特点？
【探究2】数学中也能发现很多对称问题，回忆我们学过的函数，列举若干使它 们具有类似的对称特点.
2．知识链接： （1）函数的奇偶性定义：
一般地，对于函数 f(x) 的定义域内的任意一个x ，都有 f (-x)= f (x) ，那么 f (x) 就叫做偶函数（如： f (x)=x2 , f (x)= | x |等）．
§3.4函数的奇偶性
一、学习要求
1.了解图像的对称性；理解奇（偶）函数概念. 2.会利用定义判断简单函数是否为奇（偶）函数. 3.掌握奇（偶）函数图像性质.

引例1 已知函数y=x2，则 f(－2)=f(2)=4, f(－1)=f(1)=1, f(－x)=(－x)2=f(x).
第二节 函数的性质
想一想
点M(a,b)关于x轴的对称点的坐标怎么表示?
第二节 函数的性质
可以看出，函数y=x2的图像上的任意点M(x,f(x)) 关于y轴的对称点N(－x,f(x))也在y=x2的图像上，所以 函数y=x2的图像关于y轴对称，如图3-13所示.
【例1】
第二节 函数的性质
第二节 函数的性质
思考与讨论
例2是否有其他解法？
第二节 函数的性质
课堂练习
第二节 函数的性质
二、 函数的奇偶性
在初中平面几何中，我们学习了关于轴对称图形和中 心对称图形的知识.知道点M(a,b)关于y轴的对称点为M′(－ a,b)，关于原点的对称点为M″(－a,－b).
图 3-11
第二节 函数的性质
在某一区间上单调递增或 单调递减的函数叫作在这个区 间上的单调函数，该区间叫作 这个函数的单调区间.
第二节 函数的性质
【例1】
图3-12是函数y=f(x)的图像，其定义域为区间(－ 8,12)，根据图像写出函数的单调性.
图 3-12
第二节 函数的性质
解 由图像可看出：自变量x在（-8,-5）内，函 数是单调递增的，因此函数在区间（-8,-5）上是增 函数；自变量x在（-5，-2）内，函数是单调递减的， 因此在区间（-5，-2）上是减函数.类似地可看出， 函数在区间（-2，1）和（4，9）上是增函数，在区 间（1，4）和（9，12）上是减函数.
首先，我们做一个表格（表3-1）：
第一节 函数的概念及表示方法
列出表格可以很直观地反映出练习本 的本数x与付款款额y之间的关系，像这种通 过列出自变量与对应函数值的表格来表示函 数关系的方法叫作列表法. 但这种表示方法 一般不完整，如要买80本练习本，则所需 付的款额表中就没有，那么还可以用什么方 式表示呢？

第三章 函数 （知识归纳）b 、图象从左往右 下降 函数 区间知识点一：函数的有关概念例 3：（ 1）函数 yx 22x 1 的图像，开口方向为，对称轴是 ，顶点坐标是 值域： y 的取值范围 注意 ：若两个函数是同一个函数，则它 最小值为， 函数的增区间为，函数的减区间为 ，值域为1定义域： x 的取值范围们的定义域和值域要相同。

（ 2）函数 yx 2 2x 1的图像，开口方向为，对称轴是，顶点坐标是2函数值：如 f(3)即 x= 时的函数值，f(0) 即 x= 时的函数值最大值为，函数的增区间为，函数的减区间为，值域为例 1： 1、 函数 y2x 1，(2 x 5) , 则该函数的定义域为，值域，2）、 利用定义判断（或证明）函数的单调性（即作差法）x2,3x 1, f[f(1)]=2、设f ( x)则函数的定义域为,f(2)=x 32, x1 主要步骤： 1.2.3. 知识点二：如何求定义域4.当出现以下三种情况时，函数的定义域应满足的条件。

例 4：证明函数11)、若 f (x)是整式，定义域为 f (x)x2)、若 f ( x)是分式，定义域为3)、若 f (x)是二次根式，定义域为任取 x 1， x 2定义域 ，且 x 1<x 2；写出 f(x 1) ， f(x 2 ) 的具体表达式；作 f(x 1) 与 f(x 2) 的差，比较其大小。

写结论在（ 0， +∞ ）上是增函数。

例 2：求下列函数的定义域(1) f (x)4 x 3 3x(2)f ( x)9 x 2 知识点四：函数的奇偶性x函数奇偶性的判断方法： (1) 、图像法。

（若图象关于y 轴对称则是，若图象关于原点对称则是）(2) 、根据定义采用 作差法。

步骤如下： 一看 （即看定义域是否关于原点对称，若不对称则是 函数，若对称继续进行下一步）二找 （即找 f(-x) 与 f(x) 的大小关系）。

三写结论知识点三：函数的单调性增函数： 随着 的增大而 变化相同)单调性y x ____(减函数随着的增大而 （变化相反）: y x1）、根据图象判断函数的单调性（即图象法）a 、图象从左往右 上升函数区间注意：二次函数 y=ax 2 +bx+c 的单调性 :是以对称轴 为分界线的 . 对称轴为例 5：判断下列函数的奇偶性（ 1） g(x) x 31（ 2） f ( x) x 4x 2 1x知识点五：函数的图像1 、一次函数（y=kx+b ） : 是一条直线（两个点确定一条直线）2、反比例函数 (y= k) ：是双曲线x3、二次函数：抛物线作二次函数的图像步骤：1）、先确定抛物线的开口方向2）、求出对称轴（即x b），和顶点坐标 . 2a3）、一般在对称轴的左右两边各任取两个x 值 , 并写出坐标）练一练1、已知函数 f ( x)ax3x,且 f(3)5,则 f (3)2、若函数y2x2mx 3 在(-∞， -2) 上是减函数，在 (-2 ， +∞ ) 上是增函数，则m=3、偶函数的定义域为区间（-4a ，a2+3），则实数 a=4、若 f(x) 是奇函数，且f(1)=5 ，则 f(-1)=5、函数y12| x1| 的定义域是2x6、奇函数 f(x)在[3,7] 上是增函数，且最小值为5，那么 f(x)在 [-7,-3]上是（）A. 增函数最小值为 -5B.增函数最大值为 -5C.减函数最小值为 -5D.减函数最大值为 -57、下列函数中是奇函数的是（）。

1中职数学学业水平考试复习（第三章）*考纲要求：（三）函数1.了解函数定义，会求形如()f x =1()f x ax b=+函数的定义域。

2.了解符号()f a 的含义，会求函数值。

3.理解函数的三种表示法（解析法、列表法、图像法），会用解析法表示函数；会用待定系数法求一次函数的解析式。

4.理解函数单调性的定义，会根据函数的单调性，比较同一单调区间内函数值的大小；能根据函数图像判断函数的单调性并写出函数单调区间。

5.理解函数的奇偶性的定义，会判断简单函数的奇偶性。

6.了解分段函数的概念，会求简单分段函数的函数值和定义域。

7.了解函数的简单应用，能借助函数的知识和方法，解决简单实际问题（注意避免复杂运算）。

第三章：函数一、选择题1、下列各点中，在函数13-=x y 的图像上的点是（ ）。

A ．（1，2） B.（3,4） C.(0,1) D.(5,6)2、函数321-=x y 的定义域为（ ）。

A ．()+∞∞-, B.⎪⎭⎫ ⎝⎛+∞⎪⎭⎫ ⎝⎛∞-,2323, C.⎪⎭⎫⎢⎣⎡+∞,23 D. ⎪⎭⎫ ⎝⎛+∞,23 3、下列函数中是奇函数的是（ ）。

A ．3+=x y B.12+=x y C.3x y = D.13+=x y4、函数34+=x y 的单调递增区间是( )。

A ．()+∞∞-, B. ()+∞,0 C. ()0,∞- D.[)∞+.05、点P （-2，1）关于x 轴的对称点坐标是（ ）。

A ．（-2，1） B.（2，1） C.(2，-1) D.(-2，-1)6、点P （-2，1）关于原点O 的对称点坐标是（ ）。

A ．（-2，1） B.（2，1） C.(2，-1) D.(-2，-1)7、函数x y 32-=的定义域是（ ）。

2A ．⎪⎭⎫ ⎝⎛∞-32, B.⎥⎦⎤ ⎝⎛∞-32, C. ⎪⎭⎫ ⎝⎛+∞,32 D.⎪⎭⎫⎢⎣⎡+∞,32 8、已知函数7)(2-=x x f ，则)3(-f =（ ）。

函数（奇偶性）；它的图像与x轴的交点为______________，与y轴的交点
为_____________．
（2）二次函数() = −2 2 − + 1的定义域为_____，值域为__________；
在____________上是增函数，在____________上是减函数；是__________
2
，所
1
一次函数为 = 10 + ，将点（1，4）代入得， 4 = 10 × 1 + ，即 = −6．
4
所以这个一次函数为 = 10 − 6，反比例函数为 = ．
随堂练习
1．填空题：
（1） 一次函数 = −3 + 7的定义域是__________，值域
是_____________，是_________函数(减或增)，它的图像与
2
是减函数；
例题讲解
例3 作出二次函数 = 2 − 2 − 3的图像，并讨论其单调性．
解 由 = 2 − 2 − 3知：a＝1，b＝－2，c＝－3，所以

−
2
=
−2−Biblioteka 2×14−2=1，
4
=
4×1×(−3)−(−2)2
4×1
= −4，
从而顶点坐标为（1，－4），对称轴方程为 = 1．
线，顶点坐标为(− ,
)，对称轴方程为 =
2
4

当
< 0时，二次函数
= 2 + + 的图像是一条开口向下的抛物线，
−
．
2��
4−2
定义域为R，值域为(−∞,
]．
4
并有如下性质： （1）当 = 0时为偶函数．

第3章 函数
3.2 函数的表示法
复习：函数的概念
设A是一个非空数集，如果对于 集合A的任意一个数 x ，按照某个 确定的法则f，有唯一确定的数y与 它对应，那么这种对应关系f就称为 集合A上的函数，记作y = f（x）其 中x叫做自变量，y叫做因变量。
任意一个 x
f
唯一确定的
y
定义A 域
值B域
生活中的实例：
•
2、不要看书，要看老师的眼睛
•
只要老师不是在一味地读教材，那老师的“话”就不可能和你低头看着的教材上的“文字”一致。头脑聪明的学生，也许能做到既集中精神听老师的话，又集中精神看眼前书上的内容。可是实际上大部分的学生都做不到这一点。
•
认真听讲的第一个阶段就是上课时间无条件地“往前看”，上课的时候看书往往很容易开小差。摒除杂念，将视线从摊在眼前的书上移开。老师讲课的时候只看前面，集中注意力听老师嘴里说出来的话，那才是认真听讲的态度。
a
S =a2
某城市一天的气温变化图
温度/°c
时间/时
• 思考：刚才所举的这些实例是不是函数？
函数的表示法：
• 1、列表法：用表格的形式表示两个变量之 间函数关系的方法
• 2、解析法：用解析式的形式表示两个变量 之间函数关系的方法
• 3、图象法：用图象的形式表示两个变量之 间函数关系的方法
1.列表法
难读到老师的表情。认真听讲不单纯是指听老师说的话，把握老师的表情和语调之类的小细节也是很有必要的。说话比平时更用力，或者表情严肃地强调的那个部分几乎百分之百地会出现在考试中。但是如果坐在后面，那种重要的提示就全都错过了。
•
与此相反，如果坐在前面，首先心情就很不同，自己比别人靠前的感觉让你听课时的态度变得更积极。与老师眼神交会的机会增多，感觉就好像是老师在做一对一个人辅导。

函数的变换：请解释中职数学第三章函数
知识点。

函数的变换：中职数学第三章函数知识点解释
函数是数学中非常重要的概念之一。

在中职数学的第三章中，我们研究了函数的变换及其相关知识。

1. 函数的定义和性质
函数通常用符号表示为 f(x)，其中 x 表示自变量，f(x) 表示函数的值。

函数的定义包括定义域、值域和对应关系。

函数的性质包括奇偶性、单调性和周期性等。

2. 基本函数的变换
在函数的变换中，我们研究了以下几种基本的变换方式：
- 平移变换：函数沿着 x 轴或 y 轴平移。

- 缩放变换：函数的图像沿着x 轴或y 轴方向进行拉伸或压缩。

- 翻转变换：函数的图像关于 x 轴或 y 轴进行翻转或关于原点
进行翻转。

这些变换可以通过改变函数的表达式来实现。

3. 复合函数与反函数
复合函数是指将一个函数的输出作为另一个函数的输入。

反函
数则是指将函数的输入和输出对调。

我们可以通过复合函数和反函
数来进一步变换函数。

4. 实际问题中的函数
函数不仅仅是数学中的概念，还可以在实际问题中应用。

在中
职数学的第三章中，我们还研究了如何使用函数来解决实际问题，
例如利息计算、投影问题等。

5. 总结
中职数学第三章的函数知识点涵盖了函数的定义、性质、变换以及在实际问题中的应用。

通过研究这些知识，我们可以更好地理解和应用函数。

以上就是中职数学第三章函数知识点的解释，希望对你有所帮助！。