圣彼得堡悖论

第7章不确定性7.1复习笔记1．风险描述——概率、期望值与方差面对未来的不确定性，消费者和经理人员要经常进行决策。

在各种可能性结果和发生的概率可知的情况下，这种不确定性常常用“风险”来描述。

（1）概率由于在存在风险的条件下，决策者不能确定经济行为的最后结果，需要用概率来描述某种结果发生的可能性。

在实际生活中，概率的形成主要是取决于经济主体自身的主观判断，既可以根据历史的经验，也可以根据直觉来判断经济行为出现的可能性，而不必拘泥于以前曾经发生过的某个具体事件。

因此对于同样的经济行为，不同的个体做出的判断可能不同，基于这些判断的经济决策也可能不同。

在对风险的描述中，概率是一个必不可少的概念，可以利用概率衡量一项决策行为的收益期望值及其风险波动性。

（2）期望值期望值衡量的是，结果不确定的事件所有可能性结果的加权平均数，权数就是经济主体的主观概率。

作为一个统计变量，期望值反映的是事件的总体趋势，即各种可能性的一个平均结果。

计算期望值的一般公式：如果经济中有n 种可能性结果X 1、X 2、…、X n ，其发生的概率分别为P 1、P 2、…、P n ，则其期望值为：11221()nn n i i i E X P X P X P X P X ==+++=∑L （3）方差方差σ2是实际值与期望值之差平方的平均值，而方差的平方根σ就是标准差，可以衡量不确定事件发生结果的波动程度。

由于方差衡量的是事件结果的波动程度，可以利用它来判断某一决策行为的风险性。

方差越大，风险越大。

2．公平赌博与期望效用假说（1）圣彼得堡悖论掷硬币直到出现正面为止。

如果在第n 次才第一次出现正面，则参与者可以得到2n 美元。

圣彼得堡悖论中赌博的期望值为：111211112ii i i i i x π∞∞=====+++++=∞∑∑期望值L L 上述期望值是无限大的，然而，没有人会花很多的钱（更不会多到无穷）去进行这种赌博。

这便产生一个悖论：在某种意义上，贝努利的赌博不值其（无穷的）期望值。

圣彼得堡实验的MATLAB模拟分析一、圣彼得堡悖论圣彼得堡悖论来自于一个掷币游戏关于概率期望值的悖论。

掷币游戏规则：设定掷出正面为成功，游戏者如果第一次投掷成功，得奖金2元，游戏结束；否则，继续投掷，第二次成功得奖金4元，游戏结束；以此类推，如果第n次投掷成功，得奖2n金元，游戏结束。

按照概率期望值的计算方法：将每一个可能结果的奖金乘以该结果发生的概率，即可得到该结果的奖金期望值，游戏的期望值即为所有可能结果的奖金期望值之和。

随着实验次数n的增加，虽然发生概率小，但奖金越来越多，且每一个结果的奖金期望值均为1，则游戏的期望值将为“无穷大”。

而且按照概率的理论，多次实验的结果将会接近于数学期望。

但是，以往经验表明“没有人愿意花25元去参加一次这样的游戏。

”这就出现了计算的期望值与实际情况的“矛盾”。

我们可以使用matlab软件模拟实验过程来解释这一问题。

二、圣彼得堡实验的matlab模拟分析由于投掷硬币得到正面和反面的概率相同（等概率事件），即p （正面）=p（反面）=0.5。

1.单轮圣彼得堡游戏的matlab模拟当游戏参与者投掷硬币出现正面时游戏结束，我们可以将每次投掷的随机值由函数rand产生。

如果该次rand函数运算结果小于等于0.5，定义为投掷出反面，游戏继续；反之，则定义为投掷出正面，游戏终止。

由于圣彼得堡游戏的不确定性，为了获得可信度较高的均值数据，需要进行多次模拟。

下面讨论中，对一次性连续多次的游戏模拟统称为一轮游戏模拟。

一轮圣彼得堡游戏由多个单次圣彼得堡游戏组成。

截取每次运行的投掷次数和奖金数额这两个结果，得到单轮多次圣彼得堡游戏的matlab模型（设本轮投掷运行为100次）。

从结果可以看出，在本轮模拟实验中单次游戏最高奖金达到32元，但是平均奖金只有10.62元，远小于32元。

同时单次游戏最大投掷次数为5，但平均投掷次数只有1.98。

为了增加实验的可靠性，减少不确定性，增加单轮游戏的次数，以此观察实验结果与单轮100次模拟实验的结果的异同，以此找出规律（程序运行5000次）。

圣彼得堡悖论名词解释圣彼得堡悖论，又称为彼得堡悖论，是一种经典的悖论问题，它在数学和哲学领域都有着广泛的应用和研究。

这个悖论问题最初由俄罗斯大作家和哲学家达斯金所提出，后来又被数学家伯努利和欧拉等人深入研究，成为了现代数学中的一个重要课题。

本文将从名词解释的角度，对圣彼得堡悖论进行详细的阐述和解释。

一、圣彼得堡悖论的定义圣彼得堡悖论是一种概率论中的悖论问题，它涉及到一个赌博游戏，游戏规则如下：在一个赌场里，有一个游戏机，它会不断地抛出一枚硬币，直到这枚硬币首次出现正面朝上为止。

每当硬币出现反面朝上时，游戏机就会停止抛硬币，然后赌徒可以选择离开游戏，或者继续玩下去。

如果赌徒决定继续玩下去，那么游戏机会再次抛出硬币，如果这次硬币正面朝上，那么赌徒就会赢得2美元，否则游戏就会继续进行下去，继续抛硬币，直到出现正面朝上为止。

每次硬币出现反面朝上，游戏机就会将赌注翻倍，也就是说，第一次出现反面朝上时，赌注为1美元，第二次出现反面朝上时，赌注为2美元，第三次出现反面朝上时，赌注为4美元，以此类推。

现在问题来了，假设你是这个赌场的赌徒，你带了100美元来玩这个游戏，你打算一直玩下去，直到赢得1000美元，那么你需要准备多少钱呢？这个问题看起来很简单，但是仔细分析一下就会发现，它涉及到一些概率论和数学问题，很容易陷入悖论的境地。

二、圣彼得堡悖论的分析为了更好地理解圣彼得堡悖论，我们需要对概率论中的一些基本概念进行解释和分析。

首先，我们需要了解期望值的概念。

期望值是指一系列数据中每个数据值乘以其概率的总和，也就是平均值。

例如，抛一枚硬币，正面朝上和反面朝上的概率都是50%，那么这个硬币的期望值就是(0.5*1+0.5*0)=0.5。

其次，我们需要了解几何级数的概念。

几何级数是指一个数列中每一项与前一项的比值相等的数列，例如1，2，4，8，16，32，64……就是一个几何级数，其中公比为2。

现在我们开始分析圣彼得堡悖论。

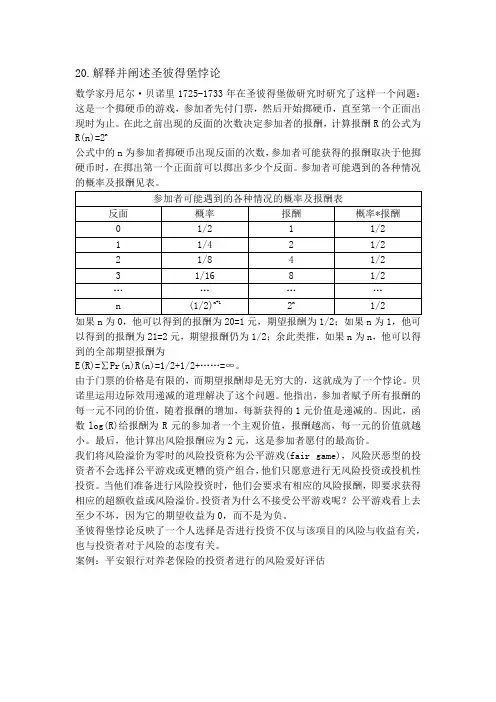
20.解释并阐述圣彼得堡悖论数学家丹尼尔·贝诺里1725-1733年在圣彼得堡做研究时研究了这样一个问题：这是一个掷硬币的游戏，参加者先付门票，然后开始掷硬币，直至第一个正面出现时为止。

在此之前出现的反面的次数决定参加者的报酬，计算报酬R的公式为R(n)=2n公式中的n为参加者掷硬币出现反面的次数，参加者可能获得的报酬取决于他掷硬币时，在掷出第一个正面前可以掷出多少个反面。

参加者可能遇到的各种情况的概率及报酬见表。

如果n为0，他可以得到的报酬为20=1元，期望报酬为1/2；如果n为1，他可以得到的报酬为21=2元，期望报酬仍为1/2；余此类推，如果n为n，他可以得到的全部期望报酬为E(R)=∑Pr(n)R(n)=1/2+1/2+……=∞。

由于门票的价格是有限的，而期望报酬却是无穷大的，这就成为了一个悖论。

贝诺里运用边际效用递减的道理解决了这个问题。

他指出，参加者赋予所有报酬的每一元不同的价值，随着报酬的增加，每新获得的1元价值是递减的。

因此，函数log(R)给报酬为R元的参加者一个主观价值，报酬越高，每一元的价值就越小。

最后，他计算出风险报酬应为2元，这是参加者愿付的最高价。

我们将风险溢价为零时的风险投资称为公平游戏(fair game)，风险厌恶型的投资者不会选择公平游戏或更糟的资产组合，他们只愿意进行无风险投资或投机性投资。

当他们准备进行风险投资时，他们会要求有相应的风险报酬，即要求获得相应的超额收益或风险溢价。

投资者为什么不接受公平游戏呢？公平游戏看上去至少不坏，因为它的期望收益为0，而不是为负。

圣彼得堡悖论反映了一个人选择是否进行投资不仅与该项目的风险与收益有关，也与投资者对于风险的态度有关。

案例：平安银行对养老保险的投资者进行的风险爱好评估。

圣彼得堡悖论柯西分布圣彼得堡悖论是一个著名的概率问题，它以俄罗斯圣彼得堡城市命名。

这个问题的核心是一个赌博游戏，游戏规则如下：每次掷一枚公平的硬币，如果正面朝上则赌金翻倍，如果反面朝上则游戏结束并且玩家输掉所有的赌金。

问题是，当游戏结束时，玩家可以预期赢得多少钱？在这个问题中，柯西分布是一个重要的概率分布。

柯西分布是一个具有无限方差的概率分布，它的形状类似于钟形曲线，但是尾部非常重。

柯西分布在圣彼得堡悖论中起到了关键的作用。

圣彼得堡悖论的精髓在于，尽管每次掷硬币的胜率只有50%，但是游戏可以无限次进行下去。

因此，玩家有可能在某次游戏中连续翻到很多次正面，从而赢得大量的钱。

虽然这种情况出现的概率非常小，但是当它发生时，赢得的金额非常高。

然而，根据柯西分布的特性，我们可以知道，柯西分布的方差是无限大的。

这意味着，圣彼得堡悖论中玩家可能赢得的金额也是无限大的。

尽管这种情况的概率非常小，但是它的存在使得玩家可以预期赢得的金额无限大。

尽管圣彼得堡悖论中玩家可以无限次地赢得金额，但是从长期来看，玩家的平均收益仍然是有限的。

这是因为每次掷硬币的胜率只有50%，玩家在大部分情况下会输掉赌金。

因此，尽管圣彼得堡悖论中存在着赢得无限金额的可能性，但是玩家在长期内的平均收益是有限的。

总结来说，圣彼得堡悖论是一个有趣的概率问题，它展示了概率和赌博的奇特性质。

柯西分布在这个问题中起到了关键的作用，它揭示了玩家可以赢得无限金额的可能性。

然而，从长期来看，玩家的平均收益仍然是有限的。

这个问题引发了对概率和赌博的深入思考，也为人们带来了对胜率和收益的重新认识。

对圣彼得堡悖论的思考
关于圣彼得堡悖论,课堂上我们亲身体验了伯努利试验,通过掷硬币的试验,也加深了自己对圣彼得堡悖论的认识.理论上来讲,圣彼得堡游戏的期望应该是无穷大的,但是通过现场投掷硬币的试验,不难发现硬币投掷者所获得的奖金的实际值并非如此.
由于首次抛掷正面向上,获5＊2＝10元奖金,第二次出现正面,5＊2＊2＝20元奖金….第n次出现正面,则或5＊2＊2＊….(n个2)元奖金,通过两轮的试验发现,第一轮庄家定价35元是稳赚不赔的,可见游戏参与者的奖金期望值,也与理论期望值是相差甚远的,在第二轮的游戏中,由于双方的竞价,庄家的定价在25元左右,游戏参与者获得了一些奖金,但每次的数额并不是很多.从游戏中发现,理论与实际的差别是很大的,在决策问题的时候,也是必须注意这种差别的,而不应该硬套理论.
若要作为本游戏的庄家,对参与游戏的人给下定价,使自己作为庄家能够获利,从实际出发来考虑的话,游戏者获得10元奖金的概率是0.5,获得20元的奖金的概率是0.25,获得40元奖金的概率是0.125,获得80元的概率也将会变得更小,获得更高奖金的几率也将是越来越小,在实际的试验中,若想出现获得高奖金的结果,一定是重复游戏多次的,在实际的游戏中,由于各种因素的限制,游戏的次数也是非常的有限的,故出现高奖金的几率也是微小的.获得40元的奖金几率几经比较小了,连续几次均获40元以上奖金的几率,将会更小,故庄家的定价定在40以内,是有利可图的.再者来看,获二十元奖金的概率也只有0.25,连续数次获得20元以上的奖金几率也是很小的,故庄家长时间经营自己的生意的话,即从长远来看,二十元钱的定价对庄家来说也是有利可图的, 故我的观点是20元以上的定价,作为庄家都是可以接受的.。

1738年，数学家丹尼尔·伯努利（Daniel Bernoulli）的堂兄尼古拉·伯努利（Nicolaus Bernoulli）提出了一个在决策学上知名的悖论—圣彼得堡悖论。

它源自一种掷币游戏—圣彼得堡游戏：假如掷出正面为赢，若玩家第一次掷出正面得奖金2元，第二次得4元，第三次得8元……直到无穷。

这个游戏的回报期望值是无穷大，但玩家中没有人愿意花25元去参加一次这样的游戏。

这是为什么呢？丹尼尔·伯努利的解释是，财富增加带给人的幸福感或曰效用（utility）是递减的。

比起这个游戏，管理者在决策时往往不知道具体的结果都有哪些、是如何分布的。

这正是经济学家弗兰克·奈特（Frank Knight）界说的“不确定性”，而“风险”是指决策者了解结果的概率分布时面临的决策情境。

比如投资5000万，一年后亏损1000万的概率是20%，盈利5000万的概率是20%，而盈亏平衡的概率是60%。

在不确定和风险情境中进行决策，是全世界管理者共同的挑战，也吸引了大量经济学家、博弈论专家、数学家、心理学家的探究。

三个参照点：现状、底线和目标人们做决策时，关注的是结果将带来的幸福感（经济学家的用语是“效用”）。

不难发现，一个人的幸福感与其总财富的多少关系并不大，而是和财富的变化密切相关。

比如，一个刚刚损失了一半身家的亿万富翁，和一个刚刚身家翻倍的农民工相比，前者的幸福感不会因为其总财富仍远远高于后者而更高。

毕竟人不是机器，对幸福的感知是相对的。

要衡量财富变化，就必须要在决策者心里设定参照点（reference point）。

2002年诺贝尔经济学奖得主丹尼尔·卡尼曼（Daniel Kahneman）和合作者艾默思·特沃斯基（Amos Tversky）提出的前景理论（prospect theory），就是以“现状”为参照点做出的理论贡献。

它以财富的现状作为零点，将其变化分为获益和损失—人们面对收益时会倾向规避风险，而面对损失时则不惜铤而走险。

圣彼得堡悖论新解与不确定性估值内容提要：著名数学家Bernoulli为解决“圣彼得堡悖论”提出了货币的边际效用递减理论（下称“效用函数解决方案”），本文通过以下两个方面证明了Bernoulli的“效用函数解决方案”是不成立的：1、用Bernoulli和克莱默的“效用函数”构造了新的悖论；2、设计并实施了不存在边际效用递减效应的“新型圣彼得堡游戏”，该游戏同样产生了“圣彼得堡悖论”。

本文进一步分析论证了人们面对不确定性前景的风险调整才是导致“圣彼得堡悖论”产生的真正原因，由此给出了不确定性决策的风险调整模型，用此模型解决了“圣彼得堡悖论”及其它相关悖论。

本文对基于不确定性的经济学理论研究提出了一个全新的研究思路和方向。

关键词：不确定性估值，圣彼得堡悖论，效用，风险调整模型，经济实验1.圣彼得堡悖论与Bernoulli的效用函数解决方案“圣彼得堡悖论”来自于一种掷币游戏，即圣彼得堡游戏。

设定掷币掷出正面为成功，游戏者如果第一次投掷成功，得奖金2元，游戏结束；第一次若不成功，继续投掷，第二次成功得奖金4元，游戏结束；这样，游戏者如果投掷不成功就反复继续投掷，直到成功，游戏结束。

如果第n次投掷成功，得奖金2n元，游戏结束。

按照概率期望值的计算方法，此游戏的期望收益为所有可能结果的得奖期望值之和：1111 ()2482 2482n nE=⨯+⨯+⨯++⨯+――――――――――――由于对于游戏中投币的次数没有理论上的限制，很显然，上式是无数个1的和，它等于无穷大，即该抽奖活动收益的数学期望值是无限的。

那么对于这样一个收益的数学期望值是无穷大的“圣彼得堡游戏”当支付多大的费用呢？试验表明，大多数人只准备支付几元钱来参加这一游戏。

于是，个人参与这种游戏所愿支付的有限价格与其收益的无穷数学期望之间的矛盾就构成了所谓的“圣彼得堡悖论”。

Bernoulli对于这个问题给出一种解决办法。

他认为人们真正关心的是奖励的效用而非它的绝对数量；而且额外货币增加提供的额外效用，会随着奖励的价值量的增加而减少，即后来广为流传的“货币边际效用递减律”。

圣彼得堡悖论解法下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts,other materials and so on, want to know different data formats and writing methods, please pay attention!圣彼得堡悖论是数学和概率论中一个著名而又深奥的悖论。

§4.2 效用函数的概念4.2.1 圣彼得堡悖论设有一个赌局，下赌注者掷一枚均匀的硬币，当出现正面反复掷下去，直到出现反面为止，如果前n 次都连续出现正面，第1+n 次出现反面，则下赌注者赢n 2元，第1次出现反面赢0元。

请问下赌注者愿意付多少赌金进行这个赌博？ 下赌注者期望赢利()+∞=⋅∑∞=1212n n n 元，虽然期望赢利为无穷大，但在实际生活中多数博彩者只愿意付不到10元才肯参与这一博彩，由此可见，人们实际决策行为与期望最优准则理论相悖。

这就是著名的圣彼得堡悖论(St.Petersburg Paradox)，由伯努利(Daniel Bernouli,1783)发现的，4.2.2 效用及效用函数（1）效用的概念（2）效用的测定 辨优设有决策系统(A,Q,V)，其结果值集合为{}n ,c ,,c c V 21=，记*c ≥()n ,c ,,c c ⋅⋅⋅21max ，0c ≤()n ,c ,,c c ⋅⋅⋅21min ，测定各结果值j c 的效用值)(j c u ，其步骤如下：①设1)(=*c u ，0)(0=c u 。

②建立简单事态体)]1([0*x c x c L -=，；，，其中x 称为可调概率。

③通过反复提问，不断改变可调概率值x ，让决策者权衡比较，当)]1(*[,0j j j p c p c L p x -==，；，时，得到无差异关系：)]1(*[~0j j j p c p c L c -=，；，。

④测得结果值j c 的效用：j j *j j p ))u(c p ()u(c p c u =-+=01)(。

不难看出，j c 的效用值就等于概率值j p 。

设决策问题的结果值集合{}n ,c ,,c c V 21=，且*c ≥()n ,c ,,c c ⋅⋅⋅21max ，0c ≤()n ,c ,,c c ⋅⋅⋅21min ，定义在c 上的实值函数)(c u 满足条件：①0)(0=c u ， 1)(*=c u ，存在V c ∈，使)(c u 满足无差异关系)),(1;),((~0*c c u c c u c -。