大学物理9热力学循环过程
- 格式:pptx
- 大小:449.65 KB
- 文档页数:13


热力学循环(thermodynamic cycle)基本定义热力学系统经过一系列传递热量并做功的热力学过程组成的集合,通过压强、温度等状态变量的变化,最终使热力学系统回到初始状态,又称循环过程。
热力学第一定律指出在一个循环中输入的净热量总等于输出的净功。
过程可重复的特性使得系统能够被连续操作,从而热力学循环是热力学中一个很重要的概念。
在实际应用中,热力学循环经常被看作是一个准静态过程并被当作实际热机和热泵的工作模型。
例如热机工作时,其中的工作物质即通过一系列的状态变化,把从高温热源吸取热量的一部分转变为机械功,将一部分废热排放到低温热源,而工作物质本身又回复到原来的状态。
由于热机要不断地工作,其中的工作物质就必须周而复始地进行这种循环过程,以不断地从热源吸取热量并对外作功。
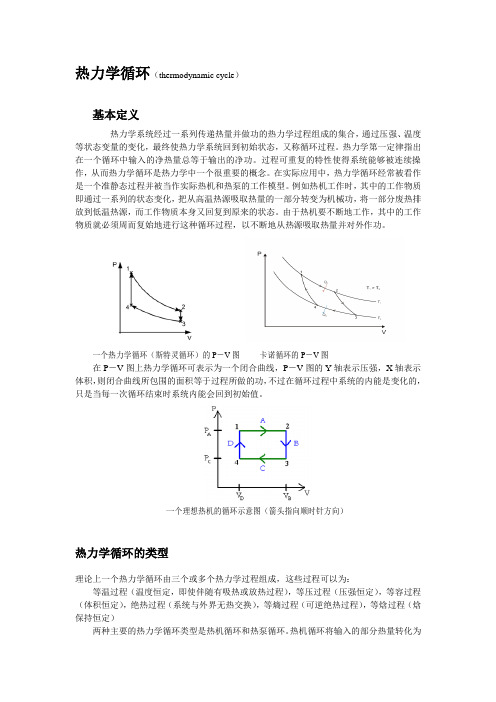
一个热力学循环(斯特灵循环)的P-V图卡诺循环的P-V图在P-V图上热力学循环可表示为一个闭合曲线,P-V图的Y轴表示压强,X轴表示体积,则闭合曲线所包围的面积等于过程所做的功,不过在循环过程中系统的内能是变化的,只是当每一次循环结束时系统内能会回到初始值。
一个理想热机的循环示意图(箭头指向顺时针方向)热力学循环的类型理论上一个热力学循环由三个或多个热力学过程组成,这些过程可以为:等温过程(温度恒定,即使伴随有吸热或放热过程),等压过程(压强恒定),等容过程(体积恒定),绝热过程(系统与外界无热交换),等熵过程(可逆绝热过程),等焓过程(焓保持恒定)两种主要的热力学循环类型是热机循环和热泵循环。
热机循环将输入的部分热量转化为输出的机械功,而热泵循环通过输入的机械功将热量从低温传向高温。
如果组成循环的全部过程都是可逆的,则称此种循环为可逆循环;如果过程中的任一部分或全部是不可逆的,则称此种循环为不可逆循环。
热机循环将输入的部分热量转化为输出的机械功,而热泵循环通过输入的机械功将热量从低温传向高温。
完全由准静态过程组成的循环能够通过控制来作为热机或热泵循环使用。



热力学循环大学物理实验中热机效率的测量热机效率是一个热力学循环中的重要参数,它衡量了热机的能源利用效率。
在大学物理实验中,测量热机效率是一个常见的实验内容。
本文将介绍热力学循环的基本原理以及如何利用实验方法准确测量热机效率。
一、热力学循环的基本原理热力学循环是指系统经过一系列状态变化后回到原始状态的过程。
在大学物理实验中,常见的热力学循环包括卡诺循环、斯特林循环和内燃机循环等。
其中,卡诺循环是一个理想化的热力学循环,通过卡诺循环的特性可以推导出热机效率的理论最大值。
卡诺循环是由两个等温过程和两个绝热过程组成的。
等温过程是指系统与热源保持恒温接触,通过吸热和放热使得系统温度保持不变。
绝热过程是指系统与外界热源没有热量交换,系统内部没有能量的转移,只有吸热或放热。
通过这样的循环,卡诺循环既能完成代表工作的过程,又能回到初始状态。
根据卡诺循环的原理,热机效率可以通过温度比来计算。
温度比是指热机工作温度与冷源温度的比值。
根据卡诺循环的分析,热机的效率等于1减去温度比。
二、热机效率的测量实验中,我们使用实际的热力学循环来测量热机的效率。
以卡诺循环为例,我们可以通过测量热源和冷源的温度来计算热机效率。
首先,我们需要确定热源和冷源的温度。
热源可以是一个恒温水槽,通过控制加热器的功率来维持一定的温度。
冷源可以是大气温度,利用室温环境即可。
其次,我们需要使用压力传感器来测量工作物质在卡诺循环的不同状态下的压力。
通过压力-体积图可以计算出等温过程和绝热过程的工作面积,并且可以得到卡诺循环的效率。
最后,我们可以利用温差计来测量热源和冷源的实际温度差。
通过将实际温度差与卡诺循环理论温度差进行比较,可以计算出热机的效率。
三、实验中需注意的问题在进行热机效率的测量实验时,还需要注意以下几个问题:1. 实验装置的绝热性:为了准确测量绝热过程的工作面积,需要确保实验装置在工作过程中与外界不发生热量交换。
2. 实验装置的恢复时间:在进行不同温度状态的转换时,需要给予足够的时间让系统达到稳定状态,以保证实验数据的准确性。
第三章热力学本章提要1.准静态过程系统连续经过的每个中间态都无限接近平衡态的一种理想过程。
准静态过程可以用状态图上的曲线表示。
2.内能系统内所有分子热运动动能和分子之间相互作用势能的和,其数学关系式为(,)E E V T=内能是态函数。
3.功功是过程量。
微分形式:VpA dd=积分形式:⎰=21dV VV pA4.热量两个物体之间或物体内各局部之间由于温度不同而交换的热运动能量。
热量也是过程量。
5.热力学第一定律热力学第一定律的数学表达式:Q E A=∆+热力学第一定律的微分表达式:d d dQ E A=+由热力学第一定律可知,第一类永动机是不可能造成的。
6.理想气体的热功转换〔1〕等体过程:d 0A = 热量增量为m m (d )d d V V MQ E C T μ,,==或m 21m 21V ,V ,MQ E E C (T T )μ=-=-〔2〕等压过程: 热量增量为(d )d d d d p Q E A E p V =+=+因m 21()V ME C T T μ∆,-=212121()()V V MA p V p V V R T T μd ==-=-⎰那么)()(21212T T R MT T R i M Q P -+-=μμ 〔3〕等温过程:d 0E =热量增量为(d )d d V Q A p V ==因2121d ln V T V V MV MA RT RT V V μμ==⎰那么2112lnln T T V pMM Q A RT RT V p μμ=== 〔4〕绝热过程:d 0Q = 根据热力学第一定路可得d d 0E A +=那么m d d d d V ,MA p V E C Tμ==-=-或221121m ()d d V V V ,V V MA E E p V C T μ=--==-⎰⎰)(112211V p V p A --=γ 在绝热过程中理想气体的p 、V 、T 三个状态参量之间满足如下关系:常量=γpV常量=-1γTV 常量=--γγT p 17.热容量等体摩尔热容量:m (d )d d d V V Q EC T T,== 等压摩尔热容量:m (d )d d d d d p p Q E VC p TT T,==+ 对于理想气体,假设分子自由度为i ,那么m 2V ,i C R = m 22P,i C R +=迈耶公式:m m p,V ,C C R =+比热容比:m m22p,V ,C i C γ+==8.焓在等压过程中,由热力学第一定律可得2121()()P Q E p V E E V V =∆+∆=-+-由于12P P P ==,上式可写为222111()()P Q E p V E pV =+-+ 如果令H E pV =+21P Q H H H =-=∆焓是一个态函数。
热力学循环大学物理中热机效率的分析与优化热力学循环:大学物理中热机效率的分析与优化热力学循环是指热机在工作过程中,被一定量的热能输入,然后进行一系列的能量转化过程,最后输出一部分的功能和功,再将剩余的热能排放出去的过程。
在大学物理中,热力学循环是一个重要的研究领域,其中热机效率的分析与优化是其中的一个关键问题。
一、热力学循环及其基本原理热力学循环是通过控制和利用热能的转化来实现各种能量转换的过程。
这些循环可以用于能源转换和机械动力等领域。
基本原理包括卡诺循环、斯特林循环和布雷顿循环等。
1.1 卡诺循环卡诺循环是热力学中最理想的循环过程之一,其基本原理是一种无损耗的热机循环。
卡诺循环由两个等温过程和两个绝热过程组成,循环的效率由源温度和汇温度来决定。
1.2 斯特林循环斯特林循环是一种理想的循环过程,它通过两个等温过程和两个等容过程来实现。
斯特林循环是一种逆摩擦热机循环,可以达到理论上的卡诺效率。
1.3 布雷顿循环布雷顿循环是一种常见的循环过程,在蒸汽机中得到广泛应用。
它由两个等压过程和两个等容过程组成。
二、热机效率的分析热机效率是衡量热机性能的重要指标,它代表了热机在能量转化过程中的效率。
热机效率可以通过以下公式计算:效率 = 输出功 / 输入热量在热机循环中,热机效率受到循环过程中能量转化的限制。
基于能量守恒和热力学第一定律,我们可以分析不同热力学循环的效率,并进行比较。
三、热机效率的优化为了提高热机效率,我们可以采取一系列优化措施。
以下是一些常见的优化方法:3.1 提高燃烧效率在内燃机中,通过改进燃烧技术和燃料选择,可以提高燃烧效率,从而提高热机效率。
3.2 优化循环过程通过调整循环过程中各个过程的参数和条件,如温度、压力和体积等,可以优化热机效率。
3.3 利用余热通过采用余热回收器等装置,将热机过程中产生的余热重新利用,可以提高热机效率。
3.4 使用高效传热材料选择具有良好传热性能的材料,优化传热器的结构和设计,可以提高热机效率。