大学物理热学总结

大学热学知识点总结图一、热力学基础知识1. 温度、热量和热平衡温度是物质内部微观运动的表现，热量是能量的一种形式，热平衡是指两个系统之间不再有能量的净传递。

2. 热力学第一定律能量守恒定律，在自然界中能量不会自行减少或增加。

3. 热力学第二定律热量不会自发地由低温物体传递给高温物体，熵增加原理。

4. 热力学第三定律当温度趋近于绝对零度时，任何实体的熵均趋于零，即系统的熵在温度趋近绝对零度时趋于一个常数。

5. 理想气体理想气体状态方程和理想气体内能的表达式。

6. 凝固和融化物质由固态转变为液态称为融化，由液态转变为固态称为凝固。

凝固和融化温度是由物质特性决定的。

二、热力学循环1. 卡诺循环卡诺循环是热机的理想循环，包括等温膨胀、绝热膨胀、等温压缩和绝热压缩四个过程。

2. 斯特林循环斯特林循环是一种热机的实际循环，包括等温膨胀、绝热膨胀、等温压缩和绝热压缩四个过程。

3. 高尔辛循环高尔辛循环是一种蒸汽轮机工作的热力循环过程，包括等压加热、等容膨胀、等压冷凝和等容压缩四个过程。

三、热力学系统1. 开放系统与闭合系统开放系统和闭合系统能够与外界进行物质、能量交换。

2. 热力学过程等容过程、等压过程、等温过程、绝热过程。

3. 热力学函数内能、焓、吉布斯自由能、哈密顿函数等热力学函数的定义和性质。

四、热传导1. 热传导的基本定律傅里叶热传导定律、傅里叶热传导方程、热导率概念。

2. 热传导的应用导热系数、传热表面积、传热温度差、传热距离等参数。

3. 热传导的热阻和导热系数热阻的概念和计算、导热系数的概念和计算。

五、热辐射1. 热辐射的基本定律斯特藩—玻尔兹曼定律、维恩位移定律、铂居—史恩定律。

2. 黑体辐射和表面发射系数黑体的定义、黑体的吸收、发射和反射的关系。

3. 热辐射的热平衡和热不平衡热辐射的观测和应用。

六、热功学1. 热功学的基本定律各态函数、热力学基本关系和亥姆霍兹自由能、君体—吉布斯函数的性质。

2. 熵增加原理和热功学过程热功学过程的熵增加原理，等熵过程、绝热过程等。

大学物理热学知识点整理热运动：物质世界的一种基本运动形式，是构成宏观物体的大量微观粒子的永不停息的无规则运动。

热现象：构成宏观物质的大量微观粒子热运动的集体表现。

宏观量：表征系统状态的物理量。

微观量：描写单个分子特征的物理量。

热力学系统，简称系统：一些包含有大量微观粒子（如分子、原子)的物体或物体系。

外界或环境：系统以外的物体。

孤立系统：与外界没有任何相互作用的热力学系统。

封闭系统：与外界没有物质交换但有能量交换的系统。

开放系统：与外界既有物质交换又有能量交换的系统。

平衡态：对于一个孤立系，经过足够长的时间后，系统必将达到一个宏观性质不随时间变化的状态，这种状态称为平衡态。

热动平衡：在平衡态下，组成系统的微观粒子仍处在不停的无规则热运动之中，只是它们的统计平均效果不变，这是一种动态的平衡，又称为热动平衡。

状态参量：在平衡态下，热力学系统的宏观性质可以用一些确定的宏观参量来描述，这种描述系统状态的宏观参量称为状态参量。

态函数：由平衡态确定的其他宏观物理量可以表达为一组独立状态参量的函数，这些物理量称为“态函数”。

体积V ：气体分子所能到达的空间，即气体容器的容积。

单位立方米（ m^{3} ）,也用升（ L ）为单位。

压强p ：气体作用与容器壁单位面积上的压力，是大量分子对器壁碰撞的宏观表现。

SI单位制中单位是帕斯卡，简称帕（ Pa ）, 1\;Pa=1\;N/m^{2} 。

有时压强的单位还用大气压（ atm ）和毫米汞柱（ mmHg ）表示。

换算关系为1\;atm=1.013\times10^{5}\;Pa1\;mm\Hg=\frac{1}{760}\;atm=1.33\times10^{2}\;Pa温度：表征物体的冷热程度的物理量。

热平衡：在与外界影响隔绝的条件下，使两个热力学系统相互接触，让它们之间能发生传热，热的系统会慢慢变冷，冷的系统会慢慢变热，经过一段时间后，它们会达到一个共同的平衡状态，称这两个系统达到了热平衡。

大学物理热学知识点整理系统吸收的热量，一部分转化成系统的内能；另一部分转化为系统对外所作的功。

Q=\Delta E+A上式的各量均为代数量，其正负号规定为：系统从外界吸热时， Q 为正，向外界放热时， Q 为负；系统对外作功时，A 为正。

外界对系统作功时， A 为负；系统内能增加时，\Delta E 为正，系统的内能减少时， \Delta E 为负。

对于状态的微小变化过程，热力学第一定律的数学表达式dQ=dE+dA第一类永动机：一种不需要外界提供能量而连续不断对外作功，系统又能复原的机器。

等体过程：dV=0 ，系统作功dA=pdV=0dQ_v=dE=\frac{M}{M_{mol}}\frac{i}{2}RdT所以 Q_v=\Delta E=E_2-E_1=\frac{M}{M_{mol}}\frac{i}{2}R(T_2-T_1)在等体过程，外界传给气体的热量全部用来增加气体的内能，系统对外不作功。

等压过程： p =恒量，当气体体积从 V_1 膨胀到 V_2 时，系统对外作功为A_p=\int_{V_1}^{V_2}pdv=p(V_2-V_1)=\frac{M}{M_{mol}}R(T_2-T_1)系统吸收的热量为Q_p=\Delta E+p(V_2-V_1)=\frac{M}{M_{mol}}(\frac{i}{2}+1)R(T_2-T_1)等温过程： \Delta E=0Q_T=A_T=\int_{V_1}^{V_2}pdv=\frac{M}{M_{mol}}RT\ln\fra c{V_2}{V_1}因为 pV=常量，即 p_1V_1=p_2V_2所以 Q_T=A_T=\frac{M}{M_{mol}}RT\ln\frac{p_1}{p_2}摩尔热容 C_m: 1mol 物质温度升高（或降低） 1K 时所吸收（或放出）的热量，单位为 J/mol\cdot K 。

C_m=\frac{(dQ)_m}{dT}理想气体等体摩尔热容：C_V=\frac{dQ_V}{dT}=\frac{dE}{dT}=\frac{\frac{i}{2}RdT }{dT}=\frac{i}{2}Ri 为分子自由度； R 为普适气体常量。

大学物理热学总结(注：难免有疏漏和不足之处，仅供参考。

教材版本：高等教育出版社《大学物理学》) 热力学基础1、体积、压强和温度是描述气体宏观性质的三个状态参量。

①温度：表征系统热平衡时宏观状态的物理量。

摄氏温标，t 表示，单位摄氏度（℃）。

热力学温标，即开尔文温标，T 表示，单位开尔文，简称开（K ）。

热力学温标的刻度单位与摄氏温标相同，他们之间的换算关系：T /K=273.15℃+ t温度没有上限，却有下限，即热力学温标的绝对零度。

温度可以无限接近0K ，但永远不能达到0K 。

②压强：气体作用在容器壁单位面积上指向器壁的垂直作用力。

单位帕斯卡，简称帕（Pa ）。

其他：标准大气压（atm ）、毫米汞高（mmHg ）。

1 atm =1.01325×105 Pa = 760 mmHg③体积：气体分子运动时所能到达的空间。

单位立方米（m 3）、升（L ）2、热力学第零定律：如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡，则这两个系统也必处于热平衡。

该定律表明：处于同一热平衡状态的所有热力学系统都具有一个共同的宏观特征，这一特征可以用一个状态参量来表示，这个状态参量既是温度。

3、平衡态：对于一个孤立系统（与外界不发生任何物质和能量的交换）而言，如果宏观性质在经过充分长的时间后保持不变，也就是系统的状态参量不再岁时间改变，则此时系统所处的状态称平衡态。

通常用p —V 图上的一个点表示一个平衡态。

（理想概念）4、热力学过程：系统状态发生变化的整个历程，简称过程。

可分为：①准静态过程：过程中的每个中间态都无限接近于平衡态，是实际过程进行的无限缓慢的极限情况，可用p —V 图上一条曲线表示。

②非准静态过程：中间状态为非平衡态的过程。

5、理想气体状态方程: 一定质量的气体处于平衡态时，三个状态参量P.V .T 存在一定的关系，即气体的状态方程()0,,=T V P f 。

理想气体p 、V 、T 关系状态方称222111T V P T V P =，设质量m ，摩尔质量M 的理想气体达标准状态，有 00000T V P M m T V P T PV m ==令00/T V P R m =,则有理想气体状体方程 RT M m PV =式中1131.8--⋅⋅=K mol J R ，为摩尔气体常量。

大学热学物理知识点总结1.热力学基本定律热力学基本定律是热学物理的基础，它包括三个基本定律，分别是热力学第一定律、热力学第二定律和热力学第三定律。

（1）热力学第一定律热力学第一定律是能量守恒定律的热学表述，它规定了热力学系统能量的守恒性质。

简单地说，热力学第一定律表明了热力学系统能量的增减只与系统对外界做功和与外界热交换有关。

热力学第一定律的数学表达式为ΔU=Q-W，其中ΔU表示系统内能的增量，Q表示系统吸热的大小，W表示系统对外界所作的功。

由此可以看出，系统的内能变化量等于吸收热量减去做的功。

（2）热力学第二定律热力学第二定律是热力学系统不可逆性的表述，它规定了热力学系统内部的熵增原理，即系统的熵不会减小，而只会增加或保持不变。

简单地说，热力学第二定律表明了热力学系统内部的任何一种热力学过程都是不可逆的。

这意味着热力学系统永远无法使热量全部转化为功，总会有一部分热量被转化为无效热。

热力学第二定律还表明了热力学过程的方向性，即热量只能从高温物体传递到低温物体，而不能反向传递。

（3）热力学第三定律热力学第三定律规定了当温度趋于绝对零度时，任何物质的熵都将趋于一个有限值，这个有限值通常被定义为零。

简单地说，热力学第三定律表明了在绝对零度时，任何系统的熵都将趋于零。

热力学第三定律的提出对于热学物理的研究具有非常重要的意义，它为我们理解热学系统的性质提供了重要的基础。

2.热力学过程热力学过程是指热力学系统内部发生的一系列变化，包括各种状态参数的变化和热力学系统对外界的能量交换。

常见的热力学过程有等温过程、绝热过程、等容过程和等压过程等。

这些过程在日常生活以及工业生产中都有着广泛的应用。

（1）等温过程等温过程是指在恒定温度下进行的热力学过程。

在等温过程中，系统对外界做的功和吸收的热量之比是一个常数。

这意味着等温过程的压强和体积成反比，在P-V图上表现为一条双曲线。

常见的等温过程有等温膨胀和等温压缩等。

（2）绝热过程绝热过程是指在无热交换的情况下进行的热力学过程。

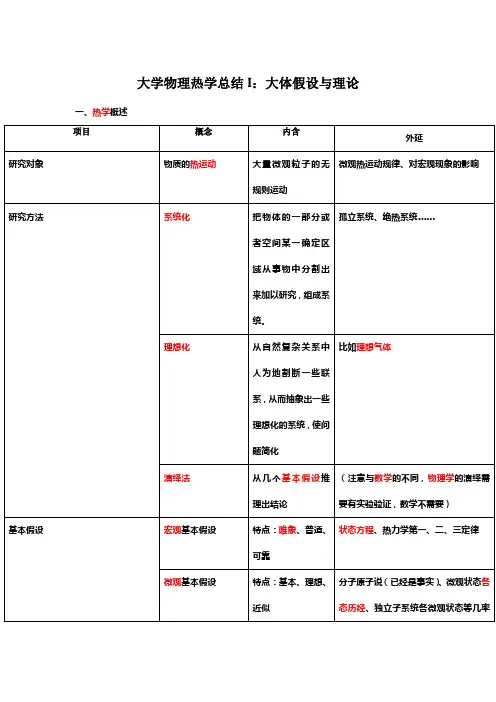
大学物理热学总结I：大体假设与理论一、热学概述二、平稳态理论（注：只有在平稳态条件下状态参量才成心义。

）三、各大体假设与大体理论下的运动。

②流体中斯托克斯公式：f=-6πaηvf：阻力a：物体半径η：粘滞系数v：运动速度③布朗粒子平均能量E̅=32k B T麦克斯韦分布律（重点）①数学概率论基础知识，重点是概率密度函数的概念、高斯分布（即正态分布）以及泊松分布（略）。

②数学上多重积分、广义积分知识（略）。

①气体分子通过碰撞达到并维持平衡态②平衡态时分子的位置与速度的概率密度函数不随时间变化③分子位置均匀分布，速度分量为高斯分布①速度分布（y、z方向完全相同）：g(v x)=√m2πk B Texp(−mv x22k B T)综合公式：f(v x,v y,v z)=(m2πk B T)32⁄exp(−mv x2+v y2+v z22k B T)②速率分布f(v)=4πv2(m2πk B T)32⁄exp(−mv22k B T)③速率分布的特征：最概然速率（概率密度最大的速率）：v p=√2k B Tm①确定函数：(1)由于平衡态各向同性，这个函数有旋转不变性，也就是速度分布只和速率有关：f(v x,v y,v z)=f(v x2+v y2+v z2)(2)方向独立：设每个方向分布函数是g①无量纲速率：定义任意速率值v=uv p，系数u是无量纲速率。

这样得到无量纲速率分布f(u)=4√πu2e−u2②麦克斯韦速率分布的实验检验：两个同心圆筒，外层转动，内层分子飞出来打到外层，由度均分原理以有大小与结构。

f B(r)=C0e−E pk B T其中C0由积分确定，对r的范围积分，结果应该为1。

进一步结论：麦克斯韦分布表现动能影响粒子在动量空间的分布：f M(v)=(√m2πk B T)3e−E kk B T波尔兹曼分布表现势能影响粒子在几何空间的分布，二者可以综合：f MB(E)=Ce−Ek B T②能量按自由度均分原理。

大学物理热学知识点一、理论基础力学1、运动学参照系。

质点运动的位移和路程，速度，加速度。

相对速度。

矢量和标量。

矢量的制备和水解。

匀速及匀速直线运动及其图象。

运动的合成。

抛体运动。

圆周运动。

刚体的对应状态和绕定轴的旋转。

2、牛顿运动定律力学中常用的几种力牛顿第一、二、三运动定律。

惯性参照系的概念。

摩擦力。

弹性力。

胡克定律。

万有引力定律。

光滑球壳对壳内和壳外质点的引力公式（不建议求出）。

开普勒定律。

行星和人造卫星的运动。

3、物体的平衡共点力促进作用下物体的均衡。

力矩。

刚体的均衡。

战略重点。

物体平衡的种类。

4、动量冲量。

动量。

动量定理。

动量守恒定律。

反冲运动及火箭。

5、机械能功和功率。

动能和动能定理。

重力势能。

引力势能。

质点及光滑球壳壳内和壳外的引力势能公式（不建议求出）。

弹簧的弹性势能。

功能原理。

机械能守恒定律。

相撞。

6、流体静力学恒定流体中的应力。

浮力。

7、振动简揩振动。

振幅。

频率和周期。

位相。

振动的图象。

参考圆。

振动的速度和加速度。

由动力学方程确认四极振动的频率。

阻尼振动。

受迫振动和共振（定性了解）。

8、波和声横波和纵波。

波长、频率和波速的关系。

波的图象。

波的干预和绕射（定性）。

声波。

声音的响度、音调和音品。

声音的共鸣。

乐音和噪声。

热学1、分子动理论原子和分子的量级。

分子的热运动。

布朗运动。

温度的微观意义。

分子力。

分子的动能和分子间的势能。

物体的内能。

2、热力学第一定律热力学第一定律。

3、气体的性质热力学温标。

理想气体状态方程。

普适气体恒量。

理想气体状态方程的微观解释（定性）。

理想气体的内能。

理想气体的等容、等压、等温和绝热过程（不要求用微积分运算）。

4、液体的性质流体分子运动的特点。

表面张力系数。

浸润现象和毛细现象（定性）。

5、液态的性质晶体和非晶体。

空间点阵。

液态分子运动的特点。

6、物态变化熔融和凝结。

熔点。

熔解热。

蒸发和凝结。

饱和汽压。

沸腾和沸点。

汽化热。

临界温度。

液态的升华。

空气的湿度和湿度计。

大学专业课热学知识点总结热学是研究热现象和热能转化规律的科学，是物理学的一个重要分支。

在大学物理专业课程中，热学作为一个重要的内容，涵盖了许多重要的知识点和理论。

本文将对大学专业课热学知识点进行总结，包括热力学定律、热力学过程、理想气体、热传导、辐射和相变等内容，并侧重于内容的清晰性和深度。

热力学定律热力学是研究热现象和热能转化规律的科学，热力学定律是热学研究的基础，包括热力学第一定律、热力学第二定律和热力学第三定律。

热力学第一定律是能量守恒定律的推广，它表明了系统的内能和对外界做功的能力之间的关系。

在热力学中，内能的变化等于系统对外界做功与热量的和，即ΔU=Q-W，其中ΔU 代表内能的变化，Q代表系统吸收的热量，W代表系统对外界做的功。

热力学第二定律是描述自然界热现象发展方向的规律，它表明了热量不能自发地从低温物体传递到高温物体，热力学第二定律还包括卡诺定理和卡诺循环等内容。

热力学第三定律是研究温度趋向绝对零度的规律，它指出了温度趋向绝对零度时，物体的熵趋于零的规律。

热力学过程热力学过程是指系统由一个平衡态转变到另一个平衡态的全过程。

在热力学中，主要研究了等体过程、等压过程、等温过程、绝热过程和多种不可逆过程等。

理想气体理想气体是热力学中常用的模型之一，它包括玻意尔定律、查理定律和瓦伦定律等内容。

在热力学中，主要研究了理想气体的状态方程、理想气体的内能、理想气体的焓和理想气体的熵等内容。

热传导热传导是研究物质内部热能传递的过程，它包括导热系数、傅里叶定律、导热方程和多种传热方式等内容。

在热力学中，主要研究了热传导的基本原理和热传导的应用。

辐射辐射是研究物体之间通过辐射方式传递热能的过程，它包括黑体辐射、辐射热力学和多种辐射计算方法等内容。

在热力学中，主要研究了辐射的基本原理和辐射的应用。

相变相变是研究物质的相变过程和相变规律的过程，它包括凝固、熔化、升华和凝华等多种物质的相变过程。

在热力学中，主要研究了相变的基本原理和相变的应用。

大学物理热力学知识点汇总热力学是大学物理中的一个重要部分，它研究的是热现象的规律以及与热相关的能量转化和传递。

以下将对大学物理热力学中的关键知识点进行汇总。

一、热力学系统和热力学平衡态热力学系统是指研究的对象，它可以是一个气体、液体或固体，也可以是由多个物体组成的系统。

而热力学平衡态则是指系统的宏观性质在长时间内不随时间变化的状态。

这包括热平衡（系统各部分温度相等）、力学平衡（系统各部分压力相等）、化学平衡（系统内各化学组分的浓度不再变化）。

二、热力学第零定律如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡，那么这两个热力学系统也必定处于热平衡。

这个定律为我们定义了温度的概念，使我们能够通过比较不同系统之间的热平衡来测量温度。

三、热力学第一定律也被称为能量守恒定律，它表明一个热力学系统内能的增量等于外界向它传递的热量与外界对它所做的功之和。

用公式表示为：ΔU ＝ Q ＋ W。

其中，ΔU 是系统内能的变化，Q 是系统吸收的热量，W 是系统对外界所做的功。

在这个定律中，需要注意功的正负。

当系统对外做功时，W 为负；外界对系统做功时，W 为正。

同样，当系统吸收热量时，Q 为正；系统放出热量时，Q 为负。

四、等容过程等容过程是指系统的体积保持不变。

在等容过程中，系统不做功（W ＝ 0），内能的变化等于吸收或放出的热量，即ΔU ＝ Q。

五、等压过程等压过程中系统的压力保持不变。

此时，系统所做的功为 W ＝pΔV，内能的变化和吸收的热量的关系为ΔU ＝Q pΔV 。

六、等温过程等温过程中系统的温度保持不变。

在理想气体的等温过程中，内能不变（ΔU ＝0），系统吸收的热量等于对外界所做的功，即Q ＝W 。

七、绝热过程绝热过程是指系统与外界没有热量交换（Q ＝0）。

在绝热过程中，系统做功导致内能变化，即 W ＝ΔU 。

八、热力学第二定律它有多种表述方式，常见的有克劳修斯表述（热量不能自发地从低温物体传到高温物体）和开尔文表述（不可能从单一热源吸取热量，使之完全变为有用功而不产生其他影响）。

大学物理热学知识点归纳总结在大学物理中，热学是一个重要的分支学科，研究热与能量的传递、转化以及物体的热性质。

下面将对大学物理热学的知识点进行归纳总结，帮助读者更好地理解和掌握这一领域的知识。

一、热传递1. 热传递方式热传递主要有三种方式：传导、对流和辐射。

传导是通过物质内部的分子碰撞传递能量；对流是通过流体的运动传递能量；辐射是通过波的传播传递能量。

2. 热传导定律热传导可以用傅里叶定律来描述，该定律表示热流密度与温度梯度成正比。

热传导系数是描述物质导热性能的物理量。

3. 对流换热对流换热是通过流体对流传热的现象，常见的例子包括空气对流、水的对流等。

对流换热可以通过牛顿冷却定律进行计算。

4. 辐射换热辐射换热是通过电磁波的辐射传递能量，不需要介质参与。

斯特藩-玻尔兹曼定律描述了辐射换热的关系，还有黑体辐射以及斯特藩定律可用于描述辐射换热的各种特性。

二、热力学1. 温度和热量温度是物体内部分子热运动的强弱程度的度量，用热力学温标来表示；热量是物体之间传递的热能。

2. 理想气体状态方程理想气体状态方程描述了气体的状态参数之间的关系，一般形式为PV = nRT，其中P是气体的压强，V是体积，n是物质的物质量，R是理想气体常数，T是温度。

3. 热力学第一定律热力学第一定律是能量守恒定律在热学过程中的表现，表示了热量与功的转化关系。

ΔU = Q - W，其中ΔU是内能变化，Q是吸收的热量，W是对外界做的功。

4. 热力学第二定律热力学第二定律描述了自然界热现象发生的方向性，主要有熵增定律和开尔文定律。

熵增定律指出自发过程的总熵增不会小于零，开尔文定律则根据热机和热泵的运行原理提出了热力学温标的概念。

三、热量传递的应用1. 热膨胀热膨胀是物体随着温度变化而引起的体积、长度等物理量的变化。

线膨胀、面膨胀和体膨胀是常见的热膨胀现象，可以通过热膨胀系数进行定量描述。

2. 热传感器热传感器是利用物体温度变化引起的一些物性变化进行温度测量的装置，如热电偶、热电阻等。

大学热学知识点总结热学是物理学中的重要分支之一，主要研究热的传递、转化以及与物质的相互作用等现象。

在大学物理课程中，热学是必不可少的一部分。

本文将对大学热学的一些基本知识点进行总结，帮助读者更好地理解热学的概念和原理。

1.温度和热平衡温度是物体内部微观粒子运动状态的一种量化描述。

热平衡是指两个物体之间没有热量交换的状态。

热平衡的条件是两个物体的温度相等，达到热平衡后，它们的温度将保持不变。

2.热量和内能热量是物体之间由于温度差而传递的能量。

内能是物体内部微观粒子的总能量，包括宏观运动能、分子势能和分子动能等。

热量的传递是由于温度差引起的内能的传递。

3.热传导热传导是指物体内部热量的传递过程。

在热传导中，热量由高温区域传递到低温区域，直到两个区域的温度达到平衡。

热传导的速率取决于物体的导热性质、温度差和物体的几何形状等因素。

4.热容和比热容热容是物体吸收或释放单位温度变化时所需的热量。

比热容是单位质量物质所需的热量。

不同物质的比热容不同，比热容可以用来比较物质的热量储存能力。

5.热膨胀热膨胀是物体在受热时体积增大的现象。

物体受热后，内部粒子的振动增强，使物体的平均间距增大，从而导致物体的体积膨胀。

热膨胀的程度可以通过热膨胀系数来描述。

6.理想气体状态方程理想气体状态方程描述了理想气体的状态和性质之间的关系。

根据理想气体状态方程，气体的压强、体积和温度之间存在一定的比例关系。

理想气体状态方程可以用来计算气体的性质和状态变化。

7.热力学第一定律热力学第一定律是能量守恒定律在热学中的应用。

根据热力学第一定律，系统吸收的热量等于系统对外界做的功和系统内能的增加之和。

热力学第一定律可以用来分析热力学系统的能量转化和守恒。

8.熵和热力学第二定律熵是一个衡量系统无序程度的物理量。

根据热力学第二定律，熵在任何孤立系统内总是增加的。

热力学第二定律描述了自然界中热量传递的方向性和不可逆性。

9.热力学循环热力学循环是指在一定条件下气体或其他工质通过一系列热力学过程完成一定的功的循环过程。