七年级数学上册 中点及角平分线讲义 (新版)新人教版

会画立体图形从 不同方向观察得 到的平面图形， 根据展开图判断 立体图形，了解 正方体的展开图
评价任务 1.借助生活实例 引入图形.2.认识 立体图形和平面 图形.3.通过练习 巩固
1.引入从不同方 向观察物体所得 到的平面图形和 展开图的概念.2. 学生动手操作.3. 总结常见立体图 形的展开图
课题
7．理解角的概念，能比较角的大小；认识度、分、秒等角的 度量单位，能进行简单的单位换算，会计算角的和、差．
8．理解余角、补角的概念，探索并掌握同角(或等角)的余角 相等、同角(或等角)的补角相等的性质．
教学目标 1.能从简单实物的外形中抽象出几何图形，理解立体图形和平
面图形的概念，会判断一个几何图形是立体图形还是平面 图形，能准确识别棱柱与棱锥. 2.从不同方向观察常见几何体及它们的组合体，并能画出从正 面、左面、上面三个方向看到的平面图形，能画出简单的 几何体的展开图. 3.认识点、线、面、体及它们之间的关系，能用它们解释生活 中的现象.
7.掌握比较角的大小的方法，能根据图形分析得出角的和、差 关系，并进行计算.
8.理解并掌握角的平分线、等分角的概念，能运用角的平分线 的概念解决问题，能进行角的乘除运算.
9.了解余角、补角的概念，能借助简单的推理，归纳出余角、 补角的性质，并能利用其解决相关问题.
课题
6.1.1 第1课时 立体图形与平 面图形
课时目标
达成目标
评价任务
6.1.2 点、线、面、 体
认识点、线、面、 知道点、线、面、 1.生活中的现象 体及它们之间的关 体是构成几何图形 引入.2.从静、动 系．区分平面和曲 的元素，能用它们 两个角度体会.3. 面、直线和曲线 解释生活中的现象 通过练习感受
6.Байду номын сангаас.1 直线、射线、 线段

七年级上册数学知识点思维导图+考点梳理有理数1.大于0的数叫做正数。

2.在正数前面加上负号“-”的数叫做负数。

3.整数和分数统称为有理数。

4.人们通常用一条直线上的点表示数，这条直线叫做数轴。

5.在直线上任取一个点表示数0，这个点叫做原点。

6.一般的，数轴上表示数a的点与原点的距离叫做数a的绝对值。

7. 由绝对值的定义可知:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。

8.正数大于0，0大于负数，正数大于负数。

9.两个负数，绝对值大的反而小。

10.有理数加法法则:(1)同号两数相加，取相同的符号，并把绝对值相加。

(2)绝对值不相等的异号两数相加，取绝对值较大的加数的负号，并用较大的绝对值减去较小的绝对值，互为相反数的两个数相加得0。

(3)一个数同0相加，仍得这个数。

11.有理数的加法中，两个数相加，交换交换加数的位置，和不变。

12.有理数的加法中，三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

13.有理数减法法则:减去一个数，等于加上这个数的相反数。

14.有理数乘法法则:两数相乘，同号得正，异号得负，并把绝对值向乘。

任何数同0相乘，都得0。

15.有理数中仍然有:乘积是1的两个数互为倒数。

16.一般的，有理数乘法中，两个数相乘，交换因数的位置，积相等。

17. 三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等。

18. 一般地，一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。

19.有理数除法法则:除以一个不等于0的数，等于乘这个数的倒数。

20.两数相除，同号得正，异号得负，并把绝对值相除。

0除以任何一个不等于0的数，都得0。

21. 求n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。

在an 中，a叫做底数，n叫做指数。

22.根据有理数的乘法法则可以得出:负数的奇次幂是负数，负数的偶次幂是正数。

显然，正数的任何次幂都是正数，0的任何次幂都是0。

人教版义务教育课程标准实验教科书七年级上册4.3.2角的比较与运算教学设计一、教材分析1、地位作用：角的比较，角的和与差，角平分线是本章重要的基础知识，也是后续学习图形与几何必备的知识基础。

在本节课中，除了让学生重点掌握以上的基础知识外，还应通过大量的识图和作图训练，来培养学生的图形感，同时，还应在解决问题的过程中注意学生推理语言和能力的培养，这也是教学的难点。

2、目标和目标解析：（1）、目标：1．理解两个角的和、差、倍、分的意义；2．掌握角平分线的概念；3．会比较角的大小，会用量角器画一个角等于已知角.（2）、目标解析：①、能从图形和数量关系两个角度认识角的大小，会用度量法和叠合法比较两个角的大小；能从几何图形和数量关系两方面认识角的和与差及角平分线，知道两个角的和、差仍然是一个角，知道角的和、差或等分的度数的计算；能结合角的大小、和与差、角平分线的直观图形，用文字语言和符号语言描述它们，反之，能将它们用符号语言或文字语言所表述的图形及关系，用图形直观表示出来。

②、在学习过程中，能在回忆线段的大小、和与差、中点内容的同时，想象本节课所要学习的内容，能对学习进程心中有数；能将对线段的大小、和与差、中点的研究方法和基本套路迁移到角的相关问题研究中，不断地提出问题、分析问题、解决问题。

3、教学重、难点教学重点：角的大小、角的和与差、角平分线的意义及数量关系；感受类比的思想。

教学难点：用图形语言、文字语言、符号语言综合描述角的大小、角的和与差关系及角平分线。

突破难点的方法：通过相关旧知的复习，按照猜想、推理的思维过程进行突破。

二、教学准备：多媒体课件、导学案、三角板或直尺、量角器、剪刀，透明或半透明纸。

三、教学过程教学内容与教师活动 学生活动 设计意图一、创设情景 引入课题 问题：这两把折扇中，哪一把形成的角度大？与折扇的大小有关系吗？（板书）课题学生观察图片，获得感性认识. 让学生知道，角的概念是从实物中抽象出来的，通过学生熟悉的事物，激发学生的学习兴趣。

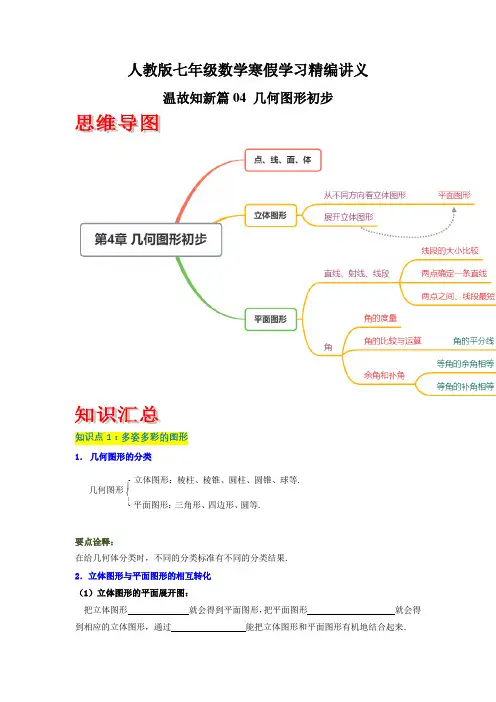
人教版七年级数学寒假学习精编讲义温故知新篇04 几何图形初步知识点1：多姿多彩的图形1． 几何图形的分类要点诠释：在给几何体分类时，不同的分类标准有不同的分类结果. 2．立体图形与平面图形的相互转化 （1）立体图形的平面展开图：把立体图形 就会得到平面图形，把平面图形 就会得到相应的立体图形，通过 能把立体图形和平面图形有机地结合起来．立体图形：棱柱、棱锥、圆柱、圆锥、球等. ⎧⎨⎩平面图形：三角形、四边形、圆等.几何图形⎧⎨⎩要点诠释：①对一些常见立体图形的展开图要非常熟悉，例如正方体的 11种展开图，三棱柱，圆柱等的展开图；②不同的几何体展成不同的平面图形，同一几何体沿不同的棱剪开，可得到不同的平面图形，那么排除障碍的方法就是：联系实物，展开想象，建立“模型”，整体构想，动手实践. （2）从不同方向看：主（正）视图---------从正面看几何体的三视图 左视图-----从左（右）边看俯视图---------------从上面看要点诠释：①会判断 的三视图. ②能根据三视图描述基本几何体或实物原型. （3）几何体的构成元素及关系几何体是由 构成的. 交成点； 成线； ， 组成.知识点2：直线、射线、线段1. 直线，射线与线段的区别与联系2. 基本性质(1)直线的性质: ． (2)线段的性质: ． 要点诠释：①本知识点可用来解释很多生活中的现象. 如：要在墙上固定一个木条，只要两个钉子就可以了，因为如果把木条看作一条直线，那么两点可 ② ，叫做两点间的距离. 3.画一条线段等于已知线段（1）度量法：可用 ,再画一条等于这个长度的线段. （2）用尺规作图法：用圆规在射线AC 上截取AB=ａ，如下图：4．线段的比较与运算 （1）线段的比较：比较两条线段的长短，常用两种方法，一种是 ；一种是 .（2）线段的和与差：如下图，有AB+BC=AC ，或AC=a+b ；AD=AB-BD 。

（3）线段的中点：把一条线段分成两条相等线段的点，叫做线段的中点．如下图，有：12AM MB AB ==要点诠释：①线段中点的等价表述：如上图，点M 在线段上，且有12AM AB =，则点M 为线段AB 的中点.②除线段的中点（即二等分点）外，类似的还有线段的三等分点、四等分点等.如下图，点M,N,P 均为线段AB 的四等分点.PNMBAAB PB NP MN AM 41==== 知识点3：角1．角的度量（1）角的定义：有 组成的图形叫做角，这个公共端点是角的顶点，这两条射线是角的两条边；此外，角也可以看作 而形成的图形.(2)角的表示方法：角通常有三种表示方法：一是用 表示，二是Cbba MBA表示，三是 表示.例如下图：要点诠释：①角的两种定义是从不同角度对角进行的定义；②当一个角的顶点有多个角的时候，不能用顶点的一个大写字母来表示. （3）角度制及角度的换算1周角= °，1平角= °，1°= ′，1′= ″，以度、分、秒为单位的角的度量制，叫做角度制. 要点诠释：①度、分、秒的换算是 进制，与时间中的小时分钟秒的换算相同.②度分秒之间的转化方法：由度化为度分秒的形式(即从 )时用乘法逐级进行；由度分秒的形式化成度(即 )时用除法逐级进行. ③同种形式相加减：度加（减）度，分加（减）分，秒加（减）秒；超60进一，减一 成60. （4）角的分类（5）画一个角等于已知角（1）借助三角尺能画出15°的 的角，在0～180°之间共能画出11个角. （2）借助 能画出给定度数的角. （3）用 法. 2．角的比较与运算（1）角的比较方法: ① ；② . （2）角的平分线：，叫做这个角的平分线，例如：如下图，因为OC 是∠AOB 的平分线，所以∠1=∠2=12∠AOB ，或∠AOB=2∠1=2∠2. 类似地，还有角的三等分线等.∠β 锐角直角钝角平角 周角 范围0＜∠β＜90° ∠β=90°90°＜∠β＜180°∠β=180°∠β=360°3．角的互余互补关系余角补角（1）若∠1+∠2=90°，则∠1与∠2互为余角.其中∠1是∠2的余角，∠2是∠1的余角. （2）若∠1+∠2=180°，则∠1与∠2互为补角.其中∠1是∠2的补角，∠2是∠1的补角. （3）结论: 相等；相等.要点诠释：①余角(或补角)是两个角的关系，是成对出现的，单独一个角不能称其为余角(或补角).②一个角的余角(或补角)可以不止一个，但是它们的度数是相同的.③只考虑数量关系，与位置无关．④“等角是相等的几个角”，而“同角是同一个角” .4．方位角以为基准，描述物体运动的方向，这种表示方向的角叫做方位角.要点诠释：（1）方位角还可以看成是将的射线旋转一定角度而形成的.所以在应用中一要确定其始边是正北还是正南.二要确定其旋转方向是向东还是向西，三要确定旋转角度的大小.（2）通常叫做东北方向，通常叫做西北方向通常叫做东南方向，通常叫做西南方向.（3）方位角在航行、测绘等实际生活中的应用十分广泛.一．选择题1．（2021秋•朝阳区校级期末）下列尺规作图，能确定AD＝BD的是（）A．B．C．D．2．（2020秋•兴业县期末）如图，OA是北偏东30°方向的一条射线，若∠BOA＝90°，则OB 的方位角是（）A．北偏西30°B．北偏西60°C．北偏东30°D．北偏东60°3．（2021秋•乌兰察布期末）如图所示，点M，N是线段AB上的两个点，且M是AB的中点，N是MB的中点，若AB＝a，NB＝b，下列结论：①AM＝a②AN＝a﹣b③MN＝a﹣b④MN ＝a．其中正确的有（）A．1个B．2个C．3个D．4个4．（2021秋•香坊区校级期中）下列说法：①两个分数相除，商一定大于被除数；②直径的长度是半径的2倍；③π是一个圆的周长与这个圆的直径的比值；④女生人数是男生人数的，则男生人数比女生人数多；⑤水结成冰，体积增加原来的；冰融化成水，水的体积是冰的．其中正确的有（）个．A．0 B．1 C．2 D．35．（2021秋•本溪期中）下列说法中正确的个数为（）（1）4a一定是偶数；（2）单项式的系数是，次数是3；（3）小数都是有理数；（4）多项式3x3﹣2xy2+25是五次三项式；（5）连接两点的线段叫做这两点的距离；（6）射线比直线小一半．A．1个B．2个C．3个D．4个6．（2021秋•龙华区期中）用一平面去截下列几何体，其截面可能是三角形的有（）A．1个B．2个C．3个D．4个7．（2021秋•雁塔区校级期中）下列图形中，不是正方体表面展开图的是（）A．B．C．D．8．（2021•宁波模拟）如图，已知矩形AEPG的面积等于矩形GHCD的面积，若要求出图中阴影部分的面积，只要知道（）A．矩形AEFD与矩形PHCF的面积之差B．矩形ABHG与矩形PHCF的面积之差C．矩形AEFD与矩形PHCF的面积之和D．矩形ABHG与矩形PHCF的面积之和9．（2020秋•封开县期末）如图，AB是一段高铁行驶路线图，图中字母表示的5个点表示5个车站在这段路线上往返行车，需印制（）种车票．A．10 B．11 C．20 D．22 10．（2003•杭州）如图所示立方体中，过棱BB1和平面CD1垂直的平面有（）A．1个B．2个C．3个D．0个二．填空题11．（2021秋•农安县期末）如图所示，∠AOC与∠BOD都是直角，且∠AOB：∠AOD＝2：11，则∠AOB＝．12．（2020秋•北海期末）如图，已知线段AB＝16cm，M是AB的中点，P是线段MB上一点，N为PB的中点，NB＝3cm，则线段MP＝cm．13．（2021秋•克东县期末）如图，是小明同学在数学实践课上，所设计的正方体盒子的平面展开图，每个面上都有一个汉字，请你判断，正方体盒子上与“答”字相对的面上的字是．14．（2020秋•天元区期末）如图，将三个同样的正方形的一个顶点重合放置，那么∠1的度数为．15．（2021秋•青羊区校级期中）已知∠AOB＝100°，射线OC在同平面内绕点O旋转，射线OE，OF分别是∠AOC和∠COB的角平分线，则∠EOF的度数为．16．（2021•胶州市一模）如图，一个正方体形状的木块，棱长为2米，若沿正方体的三个方向分别锯成3份、4份和5份，得到若干个大大小小的长方体木块，则所有这些长方体木块的表面积和是平方米．17．（2021春•东平县期末）如图，已知AB和CD的公共部分BD＝AB＝CD，线段AB，CD 的中点E，F之间的距离是10cm，则AB的长是．18．（2021春•奉化区校级期末）一副三角板AOB与COD如图1摆放，且∠A＝∠C＝90°，∠AOB＝60°，∠COD＝45°，ON平分∠COB，OM平分∠AOD．当三角板COD绕O点顺时针旋转（从图1到图2）．设图1、图2中的∠NOM的度数分别为α，β，α+β＝度．19．（2020秋•海港区校级月考）有一个不完整圆柱形玻璃密封容器如图1，测得其底面半径为a，高为h，其内装蓝色液体若干．若如图2放置时，测得液面高为；若如图3放置时，测得液面高为．则该玻璃密封容器的容积（圆柱体容积＝底面积×高）是．（结果保留π）20．（2013秋•成华区期末）如图，已知OB、OC是∠AOD内部的两条射线，OM平分∠AOB，ON平分∠COD．①若∠BOC＝40°，∠MON＝80°，则∠AOD的度数为度；②若∠AOD＝x°，∠MON＝80°，则∠BOC的度数为度（用含x的代数式表示）．三．解答题（共10小题）21．（2021秋•富裕县期末）计算：（1）；（2）；（3）80°10'35″﹣15°28′25″×3．22．（2021秋•吉林期末）如图①，将一副常规直角三角尺的直角顶点叠放在一起，∠A＝60°，∠B＝45°．解答下列问题．（1）若∠DCE＝35°24'，则∠ACB＝；若∠ACB＝115°，则∠DCE＝；（2）当∠DCE＝α时，求∠ACB的度数，并直接写出∠DCE与∠ACB的关系；（3）在图①的基础上作射线BC，射线EC，射线DC，如图②，则与∠ECB互补的角有个．23．（2021秋•吉林期末）如图，在同一直线上，有A、B、C、D四点．已知DB＝AD、AC ＝CD，CD＝4cm，求线段AB的长．24．（2021秋•七星关区期末）如图①，已知线段AB＝18cm，CD＝2cm，线段CD在线段AB 上运动，E，F分别是AC，BD的中点．（1）若AC＝4cm，则EF＝cm；（2）当线段CD在线段AB上运动时，试判断EF的长度是否发生变化？如果不变，请求出EF的长度，如果变化，请说明理由．（3）a．我们发现角的很多规律和线段一样，如图②，已知∠COD在∠AOB内部转动，OE，OF分别平分∠AOC和∠BOD，若∠AOB＝140°，∠COD＝40°，求∠EOF．b．由此，你猜想∠EOF，∠AOB和∠COD会有怎样的数量关系．（直接写出猜想即可）25．（2020秋•章丘区期末）乐乐对几何中角平分线部分的学习兴趣浓厚，请你和乐乐一起探究下面问题吧．已知∠AOB＝100°，射线OE、OF分别是∠AOC和∠COB的平分线．（1）如图1，若射线OC在∠AOB的内部，且∠AOC＝30°，求∠EOF的度数；（2）如图2，若射线OC在∠AOB的内部绕点O旋转，则∠EOF的度数；（3）若射线OC在∠AOB的外部绕点O旋转（旋转中∠AOC，∠BOC，均指小于180°的角），其余条件不变，请借助图3探究∠EOF的大小，请直接写出∠EOF的度数．（不写探究过程）26．（2021秋•平原县月考）按要求作图：如图，在同一平面内有四个点A，B，C，D．①画射线CD，画直线AD；②取线段DC的中点E，连接AE并延长，与射线BC交于点M．③连接AC并延长至点O，使AC＝CO．27．（2021秋•南岗区校级期中）小亮家的这扇门，为了达到既美观又耐用．需要让装修公司装上形状如图所示的装饰条（也包括围成阴影部分的装饰条），装饰条的宽度忽略不计，其他部分都安装上玻璃，阴影部分是在玻璃上喷上彩色的油漆．（π＝3 单位：厘米）（1）求这扇木门所用装饰条的总长度是多少厘米？（2）求喷色部分的面积是多少平方厘米？（3）若这扇门安装的玻璃每平方米200元，涂色部分的油漆每平方米500元，装饰条每米150元，这扇门的安装费用为100元，小亮家安装这扇门共需要多少元？（结果保留整数）28．（2021秋•新华区校级期中）已知∠AOB＝90°，（1）如图1，OE、OD分别平分∠AOB和∠BOC，若∠EOD＝64°，则∠BOC是°；（2）如图2，OE、OD分别平分∠AOC和∠BOC，若∠BOC＝40°，求∠EOD的度数（写推理过程）．（3）若OE、OD分别平分∠AOC和∠BOC，∠BOC＝α（0°＜α＜180°），则∠EOD的度数是（在稿纸上画图分析，直接填空）．29．（2020秋•江岸区期末）已知如图1，∠AOB＝40°．（1）若∠AOC＝∠BOC，则∠BOC＝；（2）如图2，∠AOC＝20°，OM为∠AOB内部的一条直线，ON是∠MOC四等分线，且3∠CON＝∠NOM，求4∠AON+∠COM的值；（3）如图3，∠AOC＝20°，射线OM绕着O点从OB开始以5度/秒的速度逆时针旋转一周至OB结束，在旋转过程中，设运动的时间为t，ON是∠MOC四等分线，且3∠CON＝∠NOM，当t在某个范围内4∠AON+∠BOM会为定值，请直接写出定值，并指出对应t的范围（本题中的角均为大于0°且小于180°的角）．30．（2020秋•五华区期末）已知长方形纸片ABCD，点E在边AB上，点F、G在边CD上，连接EF、EG．将∠BEG对折，点B落在直线EG上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN．（1）如图1，若点F与点G重合，求∠MEN的度数；（2）如图2，若点G在点F的右侧，且∠FEG＝30°，求∠MEN的度数；（3）若∠MEN＝α，请直接用含α的式子表示∠FEG的大小．。

人教版七年级数学上册数轴上的动点问题培优备考解题方法：1.总体来讲,解决数轴上的动点问题分为两步:(1)用未知数表示动点;(2)结合数轴,列方程.2.具体来讲,要注意以下几个问题:(1)表示动点:用未知数表示动点，常常把运动时间设为t,把握动点的出发点,运动方向和运动速度,这三个条件,例如:点A从表示1的点M出发,向右运动,速度是3个单位长度每秒,则动点A表示为:1 +3t; . 点B从表示-2的点N出发,向左运动,速度是2个单位长度每秒,则动点B表示为:-2-2t;(2)求中点:利用中点公式即可;(3)求距离:数轴上,表示两点的距离常常用右边的数减去左边的数,例如,上题动点A和B 之间的距离是:(1 +3t)-( -2-2t) =5t+3;(4)列方程:常见等量关系:一是行程中的相遇追及问题,二是线段间的和差倍分关系;(5)易错点:注意动点问题的分类讨论.例1：已知A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是【A，B】的好点。

如图1，点A表示的数为－1，点B表示的数为2。

表示1的点C到点A的距离是2，到点B的距离是1，那么点C是【A，B】的好点；表示0的点D到点A的距离是1，到点B的距离是2，是【B，A】的好点。

知识运用：如图2，M、N为数轴上两点，点M所表示的数为－2，点N所表示的数为4。

(1)数_____________所表示的点是【M，N】的好点；(2)如图3，点A所表示的数为－20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以2个单位每秒的速度向左运动，到达点A停止。

当t为何值时，P、A和B中恰有一个点为其余两点的好点？例2：数轴上有两点A，B，点C，D分别从原点O与点B出发，沿BA方向同时向左运动．（1）如图，若点N为线段OB上一点，AB=16，ON=2，当点C，D分别运动到AO，BN的中点时，求CD的长；（2）若点C在线段OA上运动，点D在线段OB上运动，速度分别为每秒1cm，4cm，在点C，D运动的过程中，满足OD=4AC，若点M为直线AB上一点，且AM-BM=OM，求AB的值．OM例3: 如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,2 秒后,两点相距16个单位长度.已知点B的速度是点A的速度的3倍.(速度单位:单位长度/秒)(1)求出点A、B运动的速度,并在数轴上标出A、B两点从原点出发运动2秒时的位置;(2)若A、B两点从(1)中标出的位置开始,仍以原来的速度同时沿数轴向左运动,经过几秒,点A、B之间相距4个单位长度?(3)若表示数0的点记为0,A、B两点分别从(1)中标出的位置同时沿数轴向左运动,经过多长时间,0B=20A.例4: 已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为90.(1)请写出与AB两点距离相等的M点对应的数;(2)现在有一只电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,你知道对应的数是多少吗?(3)若当电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q 恰好从A点出发,以2个单位/秒的速度向右运动,经过多长的时间两只电子蚂蚁在数轴.上相距35个单位长度?例5: 如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3| +(b+3a)2=0.(1)求点C表示的数;(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,若AP+BQ=2PQ,求时间t;(3)若点P从A向右运动,点M为AP中点,在P点到达点B之前:①的值不变;②2BM-BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.P A+P BP C学以致用练习:1.如图,已知A、B、C是数轴上三点,点C表示的数为6，BC=4，AB=12.(1)写出数轴.上点A、B表示的数;(2)动点P、Q分别从A、C同时出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以每秒3个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且CQ,设运动时间为t(t>0)秒.CN=13①求数轴上点M、N表示的数(用含t的式子表示);②t为何值时,原点0恰为线段PQ的中点。

北师大版 七年级(上册) 2024新版教材
第四章 基本的平面图形 小结与复习
知识梳理
基 本 平 面 图 形
直线 两点确定一条直线
线段 射线
两点之间线段最短 线段的中点 线段比较长短
角的定义
角
角平分线
角比较大小
尺规作图
知识梳理
基 本 平 面 图 形
多边形
定义 对角线 正多边形
定义
圆
弧 扇形
圆心角
知识回顾
伸
是否 可以 度量
不能 度量
不能 度量
表示方法
表示 方法
备注
作图 描述
射线 AB
A，B两点 以A为端点
有序，端 作射线
点在前
AB
直线
AB 或直 线BA 或直线
a
A，B两点
无序
过A,B两点 作直线AB
知识回顾
2.两点确定一条直线 经过两点有且只有一条直线．
二、比较线段的长度 1.线段的基本事实 两点之间的所有连线中，线段__最__短___． 简述为：两点之间，线段__最__短____ ．
基础巩固
4.下午2时15分到5时30分，时钟的时针转过的度数 为__9_7_.5_°_.
解析：时钟被分成12个大格，相当于把圆分成12等份， 每一等份等于30°. 分针转360°时，时针转一格，即30°. 从2时15分到5时30分，时针走了(3.5－0.25)格， 即30°×(3.5－0.25)＝97.5°.
知识回顾
4.角的度量 (1)角的度量单位是度、分、秒． (2)它们之间的关系是六十进制的，即1°＝60′，1′＝60″.
5.方向角 借助角表示方向，通常以正北或正南为基准，配以偏 西或偏东的角度来描述方向．

第9讲角的概念与大小比较知识定位讲解用时：5分钟A、适用范围：人教版初一，基础较好；B、知识点概述：本讲义主要用于人教版初一新课，主要学习角的概念与大小比较，掌握角的概念及角的表示方法，并能进行角度的互换；能借助三角尺画一些特殊角，掌握角大小的比较方法；会利用角平分线的意义进行有关表示或计算；掌握角的和、差、倍、分关系，并会进行有关计算.知识梳理讲解用时：15分钟角的定义及其表示方法(1)角的定义：有公共端点的两条射线组成的图形叫做角，这个公共端点是角的顶点，这两条射线是角的两条边．角也可以看作是由一条射线绕着它的端点旋转而形成的图形．当终边和始边成一条直线时，形成等角；当终边和始边重合时，形成周角．(2)角的表示方法：有四种表示角的方法：①用一个阿拉伯数字表示单独的一个角，在角内用一段弧标注；②用一个大写英文字母表示单独的一个角，当角的顶点处有两个或两个以上的角时，不能用这种方法表示角；③用一个小写希腊字母表示单独的一个角；④用三个大写英文字母表示任意一个角，这时表示顶点的字母一定要写在中间．角的理解(1)角的大小与边的长短无关，只与构成角的两条射线张开的幅度大小有关，角可以度量，可以比较大小，可以进行运算；(2)如果没有特别说明，所说的角都是指小于平角的角．1.角度制：以度、分、秒为单位的角的度量制，叫做角度制．2.角度的换算：角的度量单位是度、分、秒，把一个周角360等分，每一份就是1度的角，记作1°；把1度的角60等分，每一份就是1分的角，记作1′；把1分的角60等分，每一份就是1秒的角，记作1″.角度的换算(1)度、分、秒的换算是60进制，与时间中的时、分、秒的换算相同； (2)角的度数的换算有两种方法：①由度化成度、分、秒的形式(即从高位向低位化)，用乘法，1°＝60′， 1′＝60″；①由度、分、秒化成度的形式(即从低位向高位化),1″⎝ ⎛⎭⎪⎫＝160′，1′⎝ ⎛⎭⎪⎫＝160°，用除法．注意：度及度、分、秒之间的转化必须逐级进行转化，“越级”转化容易出错．1.角的比较： （1）度量法：用量角器量出角的度数，然后按照度数比较角的大小，度数大的角大，度数小的角小；反之，角大度数大，角小度数小． （2）叠合法：把两个角的顶点和一边分别重合，另一边放在重合边的同旁，通过另一边的位置关系比较大小． 技巧 角的比较 ①在度量法中，注意三点：对中、重合、度数；②在叠合法中，要注意顶点重合，一边重合，另一边落在重合这边的同侧．2.角的和差：角的和、差有两种意义，几何意义和代数意义．几何意义对于今后读图形语言有很大帮助，代数意义是今后角的运算的基础．①几何意义：如图所示，①AOB与①BOC的和是①AOC，表示为①AOB＋①BOC＝①AOC；①AOC与①BOC的差为①AOB，表示为①AOC－①BOC＝①AOB.①代数意义：如已知①A＝23°17′，①B＝40°50′，①A＋①B就可以像代数加减法一样计算，即①A＋①B＝23°17′＋40°50′＝64°7′，①B－①A＝40°50′－23°17′＝17°33′.3.角的平分线：从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线．如图所示，射线OC是①AOB的平分线，则有①1＝①2＝12①AOB或①AOB＝2①1＝2①2.角的平分线的理解角的平分线是一条射线，不是线段，也不是直线，它必须满足下面的条件：①是从角的顶点引出的射线，且在角的内部；②把已知角分成了两个角，且这两个角相等．课堂精讲精练【例题1】以点O为端点引3条射线时，共有个角，引4条射线时，共有个角，以点O为端点引n条射线时，共有个角（用含n的字母表示）．【答案】3、6、．【解析】解：以点O为端点引3条射线时，共有1+2=3个角；引4条射线时，共有1+2+3=6个角；以点O为端点引n条射线时，共有1+2+3+…+n﹣1=个角，故答案为：3、6、．讲解用时：5分钟解题思路：有公共顶点的n条射线，可构成n（n﹣1）个角，依据规律回答即可．教学建议：考查角的概念，掌握其规律是解题的关键．有公共顶点的n条射线，一共可构成n（n﹣1）个角．难度： 3 适应场景：当堂例题例题来源：无【练习1.1】能用∠α、∠AOB、∠O三种方式表示同一个角的图形是（）A．B．C．D．【答案】D．【解析】解：A、因为顶点O处有四个角，所以这四个角均不能用∠O表示，故本选项错误；B、因为顶点O处只有一个角，所以这个角能用∠O、∠α及∠AOB表示，故本选项正确；C、因为顶点O处有三个角，所以这三个角均不能用∠O表示，故本选项错误；D、因为∠O与∠α表示的不是同一个角，故本选项错误．故选：B．讲解用时：3分钟解题思路：根据角的表示方法进行逐一分析，即角可以用一个大写字母表示，也可以用三个大写字母表示．其中顶点字母要写在中间，唯有在顶点处只有一个角的情况，才可用顶点处的一个字母来记这个角，否则分不清这个字母究竟表示哪个角．角还可以用一个希腊字母（如∠α，∠β，∠γ、…）表示，或用阿拉伯数字（∠1，∠2…）表示．教学建议：熟知角的三种表示方法．难度： 3 适应场景：当堂练习例题来源：无35.42°=度分秒40°25′48″=．【答案】35，25，12；40.43°．【解析】解：35.42°=35度25分12秒40°25′48″=40°25.8′=40.43°，故答案为：35，25，12；40.43°．讲解用时：5分钟解题思路：：根据大单位化小单位乘以进率，小单位华大单位除以进率，可得答案．教学建议：要求学生熟练掌握度、分、秒的换算难度： 3 适应场景：当堂例题例题来源：无【练习2.1】0.15°=′″．【答案】9，0．【解析】解：解：0.15°=9′0″．故答案为：9，0．讲解用时：3分钟解题思路：根据大单位化小单位乘以进率，可得答案．教学建议：考查度分秒的换算，大单位化小单位是乘以进率60难度： 3 适应场景：当堂练习例题来源：无计算：（1）48°39′+67°31′﹣21°17′；（2）23°53′×3﹣107°43′÷5．【答案】（1）94°53′；（2）50°6′24″．【解析】解：（1）48°39′+67°31′﹣21°17′=116°10′﹣21°17′=94°53′；（2）23°53′×3﹣107°43′÷5=71°39′﹣21°32′36″=50°6′24″．讲解用时：6分钟解题思路：（1）根据度分秒加法计算法则进行解答．（2）先进行度、分、秒的乘法计算，再从左往右依次计算．教学建议：要求学生熟练掌握度、分、秒的换算难度： 3 适应场景：当堂例题例题来源：无【练习3.1】计算15°23′×4的结果是（）A．60°92′B．60.92°C．60°32′D．61°32′【答案】D【解析】解：15°23′×4=60°92′=61°32′，故选：D．讲解用时：3分钟解题思路：根据度分秒的乘法，先从小单位算起，满60时向上一单位近1，可得答案．教学建议：本题考查了度分秒的换算，度分秒的乘法，先从小单位算起，满60时向上一单位近1．难度： 3 适应场景：当堂例题例题来源：无【例题4】如图，回答下列问题：（1）比较∠FOD与∠FOE的大小；（2）借助三角板比较∠DOE与∠BOF 的大小；（3）借助量角器比较∠AOE与∠DOF的大小．【答案】（1）FOD＜∠FOE；（2）∠DOE＞∠BOF；（3）∠AOE=∠DOF.【解析】解：（1）∵OD在∠FOE的内部，∴FOD＜∠FOE．（2）用含有45゜角的三角板比较，可得∠DOE＞45゜，∠BOF＜45゜，则∠DOE＞∠BOF．（3）用量角器度量得∠AOE=30゜，∠DOF=30゜，则∠AOE=∠DOF．讲解用时：6分钟解题思路：（1）根据OD边在∠FOE内部，即可得出∠FOD＜∠FOE．（2）用量角器量∠DOE大于45゜，∠DOF小于45゜，即可得出∠DOE＞∠DOF．（3）用量角器量出角的度数，再比较大小即可．教学建议：此题考查角的大小比较，会用量角器估算角的大小难度： 3 适应场景：当堂例题例题来源：无【练习4.1】已知O是直线AB上一点，OC是一条射线，则∠AOC与∠BOC的关系是（）A．∠AOC一定大于∠BOCB．∠AOC一定小于∠BOCC．∠AOC一定等于∠BOCD．∠AOC可能大于、等于或小于∠BOC【答案】D．【解析】解：如图所示，∴∠AOC可能会大于、小于、等于∠BOC．故选：D．讲解用时：5分钟解题思路：根据题意发现，此题没有图形，那么我们应该通过分类讨论的方法，画出图形，由OC不同的位置，即可判断．教学建议：角的比较大小，当题目中没有给出图形时，要考虑全面，分情况去讨论．难度： 3 适应场景：当堂练习例题来源：无【例题5】18．如图，∠1=∠2=∠3=∠4．（1）那么OD是的角平分线，OE是是的角平分线，OC是的角平分线；（2）=4∠1，==3∠1；（3）∠BOD=∠BOC=∠AOB；（4）若∠BOE=30°，那么∠AOE=．【答案】（1）①AOB和①COE；①BOD；①AOD；（2）①AOB；①BOC；①AOE；（3）；；（4）90°．【解析】解：（1）OD是∠AOB和∠COE的角平分线，OE是∠BOD是的角平分线，OC是∠AOD的角平分线；（2）∠AOB=4∠1，∠BOC=∠AOE=3∠1；（3）∠BOD=∠BOC=∠AOB；（4）若∠BOE=30°，那么∠AOE=90°，讲解用时：6分钟解题思路：根据角平分线的定义、结合图形进行解答即可．教学建议：掌握角平分线是经过角的顶点把这个角分成相等的两个角的射线．难度： 3 适应场景：当堂例题例题来源：无【练习5.1】如图，OC平分∠AOB，OD平分∠AOC，已知∠AOD=15°，则∠BOC=．【答案】30°．【解析】解：∵OD平分∠AOC，∠AOD=15°，∴∠AOC=2∠AOD=30°，∵OC平分∠AOB，∴∠BOC=∠AOC=30°，故答案为：30°．讲解用时：4分钟解题思路：直接利用角平分线的性质分别分析得出答案．教学建议: 正确把握角平分线的定义是解题关键．难度： 3 适应场景：当堂练习例题来源：无【例题6】已知∠A0B=90°，OM平分∠AOB，在∠AOB的外部由点O引出两条射线OC、OD，若∠COD=150°，∠COM：∠DOM=3：2，求∠COB的大小.【答案】81°或171°或45°或135°．【解析】解：作出图形，①射线OC和射线OB相邻∵∠COM：∠DOM=3：2，∠COD=150°，∴∠COM=126°，∵∠AOM=∠BOM=45°，∴∠BOC=126°﹣45°=81°，②射线OC和射线OA相邻，∵∠COM：∠DOM=3：2，∠COD=150°，∴∠COM=126°，∵∠AOM=∠BOM=45°，∴∠AOC=126°﹣45°=81°，∴∠BOC=81°+90°=171°．③∠AOB是在∠COD内部，∵∠COM：∠DOM=3：2，∠COD=150°，∴∠COM=90°，∵∠AOM=∠BOM=45°，∴∠AOC=45°或135°，讲解用时：10分钟解题思路：作出图形，根据题意可以求得∠COM的值，再分类讨论与OC相邻射线是OA还是OB，即可求得∠BOC的值；教学建议：考查平分线的性质，注意引导学生分类讨论.难度： 3 适应场景：当堂例题例题来源：无如图，已知∠AOB=α，OA1平分∠AOB，OA2平分∠AOA1，OA3平分∠A0A2，…，OA n平分∠A0A n﹣1，则∠AOA n的大小为．【答案】α【解析】解：∵∠AOB=α，OA1平分∠AOB，∴∠AOA1=∠AOB=，∵OA2平分∠AOA1，∴∠AOA2=∠AOA1=α，同理∠AOA3=∠AOB=α，∠AOA4═∠AOB=α，…，∠AOA n=α讲解用时：6分钟解题思路：根据角平分线定义，再归纳总结，求出答案．教学建议：本题主要考查学生的计算能力；找出规律是解决问题的关键．难度： 3 适应场景：当堂练习例题来源：无从点O引出三条射线OA，OB，OC，已知∠AOB=30°，在这三条射线中，当其中一条射线是另两条射线所组成角的平分线时，则∠AOC=【答案】15°或30°或60°．【解析】解：①当OC平分∠AOB时，∠AOC=∠AOB=15°；②当OA平分∠BOC时，∠AOC=∠AOB=30°；③当OB平分∠AOC时，∠AOC=2∠AOB=60°．故答案为：15°或30°或60°．讲解用时：8分钟解题思路：依据一条射线是另两条射线所组成角的平分线，分三种情况进行讨论，依据角平分线的定义，即可得到∠AOC的度数．教学建议：考查平分线的性质，注意引导学生分类讨论.难度： 3 适应场景：当堂练习例题来源：无【例题7】如图，OM是∠AOC的平分线，ON是∠BOC的平分线．（1）如图1，当∠AOB是直角，∠BOC=60°时，∠MON的度数是多少？（2）如图2，当∠AOB=α，∠BOC=60°时，猜想∠MON与α的数量关系；（3）如图3，当∠AOB=α，∠BOC=β时，猜想：∠MON与α、β有数量关系吗？如果有，指出结论并说明理由．【答案】（1）45°；（2）∠MON=α；（3）∠MON=α．【解析】解：（1）如图1，∵∠AOB=90°，∠BOC=60°，∴∠AOC=90°+60°=150°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC=∠AOC=75°，∠NOC=∠BOC=30°∴∠MON=∠MOC﹣∠NOC=45°．（2）如图2，∠MON=α，理由是：∵∠AOB=α，∠BOC=60°，∴∠AOC=α+60°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC=∠AOC=α+30°，∠NOC=∠BOC=30°∴∠MON=∠MOC﹣∠NOC=（α+30°）﹣30°=α．（3）如图3，∠MON=α，与β的大小无关．理由：∵∠AOB=α，∠BOC=β，∴∠AOC=α+β．∵OM是∠AOC的平分线，ON是∠BOC的平分线，∴∠MOC=∠AOC=（α+β），∠NOC=∠BOC=β，∴∠AON=∠AOC﹣∠NOC=α+β﹣β=α+β．∴∠MON=∠MOC﹣∠NOC=（α+β）﹣β=α即∠MON=α．讲解用时：10分钟解题思路：（1）求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON=∠MOC﹣∠NOC求出即可；（2）求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON=∠MOC﹣∠NOC求出即可；（3）求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON=∠MOC﹣∠NOC求出即可．教学建议：本题考查了角平分线定义和角的有关计算，关键是求出∠AOC、∠MOC、∠NOC的度数和得出∠MON=∠MOC﹣∠NOC．难度： 3 适应场景：当堂例题例题来源：无如图，∠AOB是直角，ON是∠AOC的平分线，OM是∠BOC的平分线．（1）当∠AOC=40°，∠MON= ；（2）当∠AOC=50°，∠MON= ；（3）当锐角∠AOC=α时，∠MON= ．【答案】（1）45°；（2）45°；（3）45°.【解析】解：（1）∠AOC=40°时，∠MON=∠MOC﹣∠CON=（∠BOC﹣∠AOC）=∠AOB=45°．（2）当∠AOC=50°，∠MON=45°．理由同（1）．（3）当∠AOC=α时，∠MON=45°．理由同（1）．讲解用时：6分钟解题思路：根据角平分线的定义可得∠MON=∠MOC﹣∠NOC=（∠BOC﹣∠AOC）=∠AOB，依次均可求解．教学建议：本题主要考查角的比较与运算和角平分线的知识点，结合图形求得各个角的大小．难度： 3 适应场景：当堂练习例题来源：无如图∠BOC=2∠AOC，OD平分∠AOB（1）若∠COD=18°，求∠AOB的度数；（2）请画出∠AOC的角平分线OE，试猜想∠DOE与∠AOC的数量关系，并说明理由．【答案】∠AOB=108°，∠DOE=∠AOC．【解析】解：（1）∵OD平分∠AOB，∴∠BOD=∠AOD，设∠BOD=∠AOD=x，则∠BOC=x+18°，∠AOC=x﹣18°，∵∠BOC=2∠AOC，∴x+18°=2（x﹣18°），解得x=54°，∴∠AOB=2x=108°，（2）结论：∠DOE=∠AOC．理由：设∠AOC=2y，则∠AOE=∠EOC=y，∠BOC=4y，∵OD平分∠AOB，∴∠AOD=3y，∴∠DOE=2y=∠AOE，∴∠DOE=∠AOC．讲解用时：8分钟解题思路：（1）设∠BOD=∠AOD=x，可得∠BOC=x+18°，∠AOC=x﹣18°，根据∠BOC=2∠AOC，构建方程即可解决问题；（2）结论：∠DOE=∠AOC．设∠AOC=2y，则∠AOE=∠EOC=y，∠BOC=4y，想办法用y表示∠DOE即可解决问题；教学建议：本题考查角的计算，角平分线的定义等知识，解题的关键是学会利用未知数构建方程解决问题，属于中考常考题型．难度： 3 适应场景：当堂例题例题来源：无【练习8.1】如图，已知∠AOB=40°，自O点引射线OC，若∠AOC：∠COB=2：3，OC与∠AOB 的平分线所成的角的度数为．【答案】4°或100°．【解析】解：（1）若OC在∠AOB内部，∵∠AOC：∠COB=2：3，∴设∠AOC=2x，∠COB=3x，∵∠AOB=40°，∴2x+3x=40°，得x=8°，∴∠AOC=2x=2×8°=16°，∠COB=3x=3×8°=24°，∵OD平分∠AOB，∴∠AOD=20°，∴∠COD=∠AOD﹣∠AOC=20°﹣16°=4°．（2）若OC在∠AOB外部，∵∠AOC：∠COB=2：3，∴设∠AOC=2x，∠COB=3x，∵∠AOB=40°，∴3x﹣2x=40°，得x=40°，∴∠AOC=2x=2×40°=80°，∠COB=3x=3×40°=120°，∵OD平分∠AOB，∴∠AOD=20°，∴∠COD=∠AOC+∠AOD=80°+20°=100°．∴OC与∠AOB的平分线所成的角的度数为4°或100°．讲解用时：8分钟解题思路：由于∠AOC：∠COB=2：3，∠AOB=40°，可以求得∠AOC的度数，OD 是角平分线，可以求得∠AOD的度数，∠COD=∠AOD﹣∠AOC．教学建议:本题考查了角的计算用到角平分线的性质，涉及到角的倍分关系时，一般通过设未知数，建立方程进行解决．难度： 3 适应场景：当堂练习例题来源：无课后作业【作业1】一个角的内部从顶点引出4条射线，则此时构成的角的个数有（）A．5个B．6个C．10个D．15个【答案】D．【解析】解：根据题意可知，角的顶点处有6条射线，共有5+4+3+2+1=15个角．故选D．讲解用时：5分钟难度： 2 适应场景：练习题例题来源：无【作业2】比较∠CAB与∠DAB时，把它们的顶点A和边AB重合，把∠CAB和∠DAB放在AB的同一侧，若∠CAB＞∠DAB，则（）A．AD落在∠CAB的内部B．AD落在∠CAB的外部C．AC和AD重合D．不能确定AD的位置【答案】A．【解析】解：比较∠CAB与∠DAB时，把它们的顶点A和边AB重合，把∠CAB和∠DAB 放在AB的同一侧，若∠CAB＞∠DAB，则AD落在∠CAB的内部．故选：A．讲解用时：3分钟难度： 3 适应场景：练习题例题来源：无【作业3】计算72°34′÷2+18°33′×4=．【答案】110°29′．【解析】解：72°34′÷2+18°33′×4=36°17′+74°12′=110°29′．故答案为：110°29′．讲解用时：5分钟难度： 3 适应场景：练习题例题来源：无【作业4】如图，已知∠AOB=α，∠COD=β，OM为∠AOD的平分线，ON为∠BOC的平分线，则∠MON=（用含α，β的式子表示）．【答案】（α+β）．【解析】解：∵∠AOB=α，∠COD=β，∴∠AOD=∠COD+∠AOC=β+∠AOC，∠BOC=∠AOB+∠AOC=α+∠AOC，∴∠BOD=∠AOD+∠BOC﹣∠AOC=α+β+∠AOC．∵OM为∠AOD的平分线，ON为∠BOC的平分线，∴∠BON=∠BOC，∠DOM=∠AOD，∴∠MON=∠BOD﹣∠BON﹣∠DOM=α+β+∠AOC﹣∠BOC﹣∠AOD=α+β+∠AOC﹣（∠BOC+∠AOD）=α+β+∠AOC﹣（α+β+2∠AOC）=α+β+∠AOC﹣α﹣β﹣∠AOC=（α+β）．故答案为：（α+β）．讲解用时：8分钟难度： 3 适应场景：练习题例题来源：无【作业5】以∠AOB的顶点O为端点引射线OP，使∠AOP：∠BOP=3：2，若∠AOB=17°，∠AOP的度数为．【答案】10.2°或51°．【解析】解：如图1，当射线OP在∠AOB的内部时，设∠AOP=3x，则∠BOP=2x，∵∠AOB=∠AOP+∠BOP=5x=17°，解得：x=3.4°，则∠AOP=10.2°，如图2，当射线OP在∠AOB的外部时，设∠AOP=3x，则∠BOP=2x，∵∠AOP=∠AOB+∠BOP，又∵∠AOB=17°，∴3x=17°+2x，解得：x=17°，则∠AOP=51°．故∠AOP的度数为10.2°或51°．故答案为：10.2°或51°．讲解用时：5分钟难度： 3 适应场景：练习题例题来源：无。

第十二讲角的初步认识（一）一、知识精讲1.角的定义角的定义一：有公共端点的两条射线组成的图形叫做角。

角的定义二：一条射线绕着它的端点旋转而形成的图形。

2.角的大小比较（1）叠合法；（2）度量法3.余角和补角如果两个角的和是90°，那么称这两个角互为余角。

如果两个角的和是180°，那么称这两个角互为补角。

4.角平分线从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线.二、典例解析【例1】（汉阳区期末）如图，在锐角∠A O B内部，画1条射线，可得3 个锐角画2条射线，可得6个锐角，画3条射线，可得10个锐角，……，按此规律，画9条不同射线，可得锐角个.【练1】如图，在∠A O B内部引出两条射线O C，O D，则图中小于平角的角共有（）个A.3B.4C.5D.6【练2】在∠A O B内部从O点引出n条射线，图中小于平角的角共有多少个？【练3】从O点引出n条射线，图中小于平角的角共有多少个？【例2】（武昌区期末）一个角的余角比它的补角的14大 15°，求这个角的度数.【练4】若∠AOB和∠BOC互为邻补角，且∠AOB比∠BOC大18°，则∠AOB的度数是（）A.54°B.81°C.99°D162°【练5】如图，O是直线A B上一点，OC，OD，OE是三条射线，则图中互补的角共有（）对A.3B.3C.4D.5【例3】（东湖开发区）如图，直线AB、CD相交于点O，OM平分∠BOD，ON 平分∠BOC，∠1∶∠2＝7∶1，求∠BOD和∠AON的度数.【例4】（江岸区期末）如图，在同一平面内，O A⊥O B于O，射线O M平分∠A O B，从点O引射线O C，射线O N平分∠B O C（1）若∠B O C＝30°，请你补全图形，再计算∠M O N的度数（2）若O A与O B不垂直，∠A O B＝α，∠B O C＝β（0＜β＜α＜90°），其它条件不变，请你画出大致图形，并直接写出M O N的度数（3）结合上面的计算，观察并继续思考：在同一平面内，∠A O B＝α，∠ B O C＝β，OM平分∠AOB，ON平分∠BOC，你发现∠MON与∠AOC有怎样的数量关系？请你直接写出来.【例5】（东湖开发区期末）8 时 30 分，钟的时针与分针成（）的角.A.75°B.90°C.105°D.120°【练6】2点30分时，时钟与分钟所成的角为度.【例6】（江汉区期末）如图，直线S N与直线WE相交于点O，射线ON表示正北方向，射线OE表示正东方向．已知射线OB的方向是南偏东m°，射线OC的方向是北偏东n°，且m°的角与n°的角互余.（1）①若m＝60，则射线OC的方向是.②请直接写出图中所有与BOE互余的角及与BOE互补的角；（2）若射线O A是∠B O N的角平分线，求∠A O C的度数（用含有m的式子表示）三、课堂检测1.（黄陂区期末）如图，已知OD平分∠AOB，OE平分∠BOD，若∠AOC=32∠BOC，则COEBOE∠∠的值为（）A.12B.23C.35D.322.（洪山区期末）如图，O为直线AB上一点，∠DOC＝90°，OE平分∠AOC，OF平分∠BOC.(1)图中与∠COF互余的角有，与∠COF互补的角有.(2)如若52∠EOD =∠AOE ，∠EOD的度数为.3.（江岸区期末）如图，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE表示正东方向．已知射线OB的方向是南偏东m°，射线OC的方向是北偏东n°，且m°的角与n°的角互余.（1）①若m＝50，则射线OC的方向是②图中与∠BOE互余的角有与∠BOE互补的角有（2）若射线OA是∠BON的角平分线，则∠BOS与∠AOC是否存在确定的数量关系？如果存在，请写出你的结论以及计算过程；如果不存在，请说明理由.四、课后练习1.（江汉区期末）9时30分钟的时针与分针所成的角度是（） A.75°B.90°C.105°D.120°2.（青山区期末）如图，在观测站O测得渔船A、B的方向分别为北偏东50°、南偏西30°，为了减少相互干扰并取得较好的捕鱼效益，渔船C恰好位于∠A O B的平分线上，则渔船C相对观测站O的方向是（A.南偏东50°B.东偏西50°C.东南方D.不能确定3.如图，在正方形网格中，∠1+∠2+∠3+∠4+∠5=（））A.175° B.180°C.210°D.225°4.（青山区期末）如图，O是直线AC上一点，OB 是一条射线，OD平分∠AOB，OE在∠BOC内，且∠DOE＝60°，∠BOE ＝∠EOC，则下列四个结论正确的个数有（）① ∠BOD＝30°；② 射线OE平分∠AOC；③ 图中与∠BOE互余的角有 2 个；④ 图中互补的角有 6对A.1 个B.2 个C.3 个D.4 个5.（洪山区期末）已知：O为直线AB上一点，一个三角板COD的直角顶点放在点O上，OE平分∠AOC，OF平分∠BOD，当三角形COD绕O点旋转到如图所示时，下列结论不正确的是（）A.∠AOD－∠EOC＝90°B.∠AOC－∠BOD＝90°C.∠AOE－∠BOF＝45°D.∠EOF＝135°6.如图，已知O为直线A B上一点，OC平分∠BOE，OD⊥OC于点O，则与∠DOE互补的角是（）A.∠EOCB．∠AOCC.∠AOED．∠BOD7.如图，∠AOB=100°OM平分∠AOC，ON平分∠BOC，则∠MNO=.8.图中的正五角星有条对称轴，图中与∠A的2 倍互补的角有个.9.如图，BO，CO分别平分∠ABC和∠ACB.（1）若∠A=60°，求∠O；（2）若∠A=100°，∠O是多少？若∠=120°，∠O又是多少？（3）若（1）、（2）你又发现了什么规律，当∠A 的度数发生变化后，你的结论仍成立吗？（提示：三角形的内角和等于180°）10.已知：∠AOD＝160°，OB、OC、OM、ON是∠AOD内的射线。

内容 基本要求略高要求较高要求找规律 学会基本的找规律方法 能做常见的找规律题型，能根据题意找出相应的对应关系 能做综合试题 定义新运算熟悉基本题型能根据题意进行运算板块一、找规律模块一、代数中的找规律【例1】 ⑴点1A 、2A 、3A 、…、 n A （n 为正整数）都在数轴上．点1A 在原点O 的左边，且11AO =；点2A 在点1A 的右边，且212A A =；点3A 在点2A 的左边，且323A A =；点4A 在点3A 的右边，且434A A =；……，依照上述规律，点2008A 、2009A 所表示的数分别为（ ）．A ．2008、2009-B ．2008-、2009C ．1004、1005-D ．1004、1004-⑵如图，点A 、B 对应的数是a 、b ，点A 在3-、2-对应的两点（包括这两点）之间移动，点B 在1-、0对应的两点（包括这两点）之间移动，则以下四式的值，可能比2008大的是（ ）． 0b-1-2a-3A ．b a -B ．1b a - C ．11a b- D ．2()a b -【巩固】 ⑴（2008北京中考）一组按规律排列的式子：2-b a ，52b a ，83-b a ，114b a，…(0≠ab )，其中第7个式子 是 ，第n 个式子是 (n 为正整数)．⑵（2008年陕西中考）搭建如图①的单顶帐篷需要17根钢管，这样的帐篷按图②、图③的方式串起来搭建，则串7顶这样的帐篷需要 根钢管.① ② ③【例2】 ⑴（2010年北京中考）右图为手的示意图，在各个手指间标记字母A B C D ，，，。

请你按图中箭头所指方向(即...A B C D C B A B C →→→→→→→→→的方式)从A 开始数连续的正整数1，2，3，4…，当数到12时，对应的字母是 ；当字母C 第201次出现时，恰好数到的数是 ；当字母C 第2n +1次出现时(n 为正整数)，恰好数到的数是 (用含n 的代数式表示)。

角平分线的性质（4种题型）【知识梳理】一、角的平分线的性质角的平分线的性质：角的平分线上的点到角两边的距离相等.要点诠释：用符号语言表示角的平分线的性质定理：若CD平分∠ADB，点P是CD上一点，且PE⊥AD于点E，PF⊥BD于点F，则PE＝PF.二、角的平分线的逆定理角平分线的判定：角的内部到角两边距离相等的点在角的平分线上.要点诠释：用符号语言表示角的平分线的判定：三、角的平分线的尺规作图角平分线的尺规作图（1）以O为圆心，适当长为半径画弧，交OA于D，交OB于E.（2）分别以D 、E 为圆心，大于DE 的长为半径画弧，两弧在∠AOB 内部交于点C. （3）画射线OC.射线OC 即为所求. 【考点剖析】题型一：角平分线性质定理 例1.（2023春·陕西榆林·八年级校考期末）如图，在四边形ABCD 中，90B C ∠=∠=︒，点E 为BC 的中点，且AE 平分BAD ∠．求证：DE 是ADC ∠的平分线．【详解】证明：如图，过点E 作EF AD ⊥于点F ，∴90B Ð=°，AE 平分BAD ∠，∴BE EF =．∴点E 是BC 的中点，∴BE CE =，∴CE EF =．又∵90C ∠=︒，EF AD ⊥，∴DE 是ADC ∠的平分线．【变式1】（2023春·山西太原·七年级校考阶段练习）如图，ABC 中，90C ∠=︒，AD 平分BAC ∠，5AB =，2CD =，求ABD △的面积．12【答案】5【详解】解：作DE AB ⊥如图，∵AD 平分BAC ∠，90C ∠=︒，2CD =，∴=2CD DE =，1152522ABD S AB DE ∴=⨯⨯=⨯⨯=△．【变式2】（2023春·湖南常德·八年级统考期末）如图，点P 是ABC 的三个内角平分线的交点，若ABC 的周长为24cm ，面积为236cm ，则点P 到边BC 的距离是（ ）A ．8cmB ．3cmC ．4cmD ．6cm【答案】B 【详解】解：过点P 作PD AB ⊥于，PE BC ⊥于E ，PF AC ⊥于F ，如图，∵点P 是ABC 的内角平分线的交点，∴PE PF PD ==，又ABC 的周长为24cm ，面积为236cm ，∴()11112222ABC S AB PD BC PE AC PF PE AB BC AC =⋅+⋅+⋅=++，∴124363PE ⨯⨯=∴3cm PE =【变式3】（湖南省郴州市2022-2023学年八年级下学期期末数学试题）如图，在ABC 中，90ACB ∠=︒，BD 平分ABC ∠，DE AB ⊥于点E ．如果8AC =，那么AD DE +=______．【答案】8【详解】解：∵在ABC 中，90ACB ∠=︒，BD 平分ABC ∠，DE AB ⊥，∴CD DE =，∵8AC =，∴8AD DE AD CD AC +=+==， 【变式4】（2023春·广东深圳·七年级统考期末）把两个同样大小的含30︒角的三角尺像如图所示那样放置，其中M 是AD 与BC 的交点，若4CM =，则点M 到AB 的距离为______．【答案】4【详解】解：由题意，得：90,30D C ABC DAB ∠=∠=︒∠=∠=︒，∴,60MC AC CAB ⊥∠=︒，∴30MAC BAC MAB MAB ∠=∠−∠=︒=∠，∴AM 平分DAB ∠，过点M 作MN AB ⊥，交AB 于点N ，∴4MN MC ==．故答案为：4．【变式5】如图，P 为ABC 三条角平分线的交点，PH 、PN 、PM 分别垂直于BC 、AC 、AB ，垂足分别为H 、N 、M ．已知ABC 的周长为15cm ，3cm PH =，则ABC 的面积为______2cm ．【答案】22.5【详解】解：连接PM 、PN 、PH ，P 为ABC 三条角平分线的交点，PH 、PN 、PM 分别垂直于BC 、AC 、AB ，3cm PM PN PH ∴===，ABC ∴∆的面积ΔAPB =的面积ΔBPC +的面积ΔAPC +的面积111222AB PM BC PH AC PN =⨯⨯+⨯⨯+⨯⨯ 1()32AB BC AC =++⨯222.5(cm )=．七年级校考期末）如图，在ABC 中，【答案】(1)32︒ (2)6【详解】（1）解：∵40B ∠=︒，76C ∠=︒，∴180407664BAC ∠=︒−︒−︒=︒，∵AD 平分BAC ∠， ∴1322BAD BAC ∠=∠=︒；（2）如图，过点D 作DF AB ⊥于点F ，∵AD 平分BAC ∠，DE AC ⊥，∴DF DE =，∵2DE =，6AB =，∴2DF =， ∴ABD △的面积12662=⨯⨯=.题型二：角平分线性质定理及证明 ，且PMN 与OMN 的面积分别是【答案】(1)证明过程见详解(2)20OM ON +=【详解】（1）证明：如图所示，过P 作PC MN PD OA PE OB ⊥⊥⊥，，，∵MP 平分AMN ∠，NP 平分MNB ∠，∴PD PE =，PC PE =，∴PD PE =，∵PD AO PE BO ⊥⊥，，∴OP 平分AOB ∠．（2）解：如图所示，过P 作PC MN PD OA PE OB ⊥⊥⊥，，，连接OP ，∵18162PMN MN S MN PC ===△，，∴4PC =，由（1）可知4PD PE PC ===，∵1624PMN OMN S S ==△△，，∴40MONP S =四边形，即1122OPM ONP MONP S S S OM PD ON PE =+=+△△四边形，∴1140442222OM ON OM ON =⨯+⨯=+，∴20OM ON +=． 【变式1】（2022秋·河南安阳·八年级校考阶段练习）如图，点E 是BC 的中点，AB BC DC BC ⊥⊥，，AE 平分BAD ∠．求证：(1)DE 平分ADC ∠；(2)AD AB CD +＝．【详解】（1）证明：如下图，过E 作EF AD ⊥于F ，∵AB BC ⊥，AE 平分BAD ∠，∴EB EF ＝，∵点E 是BC 的中点，∴EB EC ＝，∴EF EC ＝，∵DC BC EF AD ⊥⊥，，∴90EFD ECD ∠∠︒＝＝，在Rt EFD 和Rt ECD △中，EF EC ED ED =⎧⎨=⎩，∴Rt Rt HL EFD ECD ≌（），∴FDE CDE ∠∠＝，∴DE 平分ADC ∠；（2）解：由（1）知，Rt Rt EFD ECD ≌，∴FD CD ＝，在Rt AEF 和Rt AEB 中，EF EB AE AE =⎧⎨=⎩，∴Rt Rt HL AEF AEB ≌（），∴AF AB ＝，∵AD AF FD +＝，∴AD AB CD +＝．【变式2】（2022秋·北京朝阳·八年级校考期中）如图，在ABC ∆中，90C ∠=︒，DE AB ⊥，于点E ，AD 平分CAB ∠，点F 在AC 上，BD DF =．求证：BE FC =．【详解】证明：∵AD 平分CAB ∠，90C ∠=︒，DE AB ⊥，∴DE DC =，90C DEB ∠=∠=︒，∴在Rt DEB ∆和Rt DCF ∆中，∵DE DC BD DF =⎧⎨=⎩，∴()HL DEB DCF ∆≅∆，∴BE FC =．(1)求证：BE ＝CD ；(2)判断点O 是否在∠BAC 的平分线上，并说明理由．（1）证明：BE 、CD 是ABC ∆的高，且相交于点O ，90∴∠=∠=︒BEC CDB ，在BDO ∆和CEO ∆中，90CDB BEC BOD COEBD CE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，BOD COE ∴∆≅∆(AAS)，OD OE ∴=，OB OC =，OD OC OE OB ∴+=+，即CD BE =；（2）解：点O 在BAC ∠的平分线上，理由如下： 连接AO ，如图所示：BE 、CD 是ABC ∆的高，且相交于点O ， 90ADC AEB ∴∠=∠=︒，由（1）得BE CD =，∴在ABE ∆和ACD ∆中，90ADC AEB CAD BAE CD BE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，ACD ABE ∴∆≅∆(AAS)， AD AE ∴=，由（1）得OD OE =，∴在AOD ∆和AOE ∆中，90AD AE ADC AEB OD OE =⎧⎪∠=∠=︒⎨⎪=⎩，AOD AOE ∴∆≅∆(SAS)，DAO EAO ∴∠=∠， ∴点O 在BAC ∠的平分线上．题型三：角平分线的判定定理 例3.如图，90B C ∠=∠=︒，M 是BC 的中点，AM 平分DAB ∠，求证：DM 平分ADC ∠．【详解】证明：如图：过点M 作ME AD ⊥，垂足为E ，AM 平分DAB ∠，MB AB ⊥，ME AD ⊥，ME MB =∴（角平分线上的点到角两边的距离相等），又MC MB =，ME MC ∴=，MC CD ⊥，ME AD ⊥，DM ∴平分ADC ∠（到角的两边距离相等的点在这个角的平分线上）．【详解】（1）证明：如图，过点E 作EF DA ⊥于点F ，∵90C ∠=︒，DE 平分ADC ∠，∴CE EF =，∵E 是BC 的中点，∴BE CE =，∴BE EF =，又∵90B Ð=°，EF DA ⊥，∴AE 平分DAB ∠．（2）解：∵EF DA ⊥，90C ∠=︒，∴EFD △和ECD 都为Rt △，又∵DE 平分ADC ∠，∴EC EF =，在Rt EFD 和Rt ECD △中，ED ED EC EF =⎧⎨=⎩，∴()Rt Rt HL EFD ECD △≌△， ∴EFD ECD S S =△△，CED FED ∠=∠，∵EF DA ⊥，90B Ð=°，∴EFA △和EBA △都为Rt △，又∵AE 平分DAB ∠，∴EF EB =，在Rt EFA △和Rt EBA △中，EA EA EF EB =⎧⎨=⎩，∴()Rt Rt HL EFA EBA △≌△， ∴EFA EBA S S =△△，FEA BEA ∠=∠， ∴()111809022DEA DEF AEF CEF BEF ∠=∠+∠=∠+∠=⨯︒=︒， ∵4AE =，3DE =， ∴1143622AED S AE DE =⋅=⨯⨯=△， ∴EFD ECD EFA EBA ABCD S S S S S =+++△△△△四边形EFD EFD EFA EFA S S S S =+++△△△△()2EFD EFA S S =+△△2AED S =△ 26=⨯12=．∴四边形ABCD 的面积为12． 【变式2】如图，在AOB 和COD △中，OA OB =，OC OD =（OA OC <），AOB COD α∠=∠=，直线AC ，BD 交于点M ，连接OM ．(1)求证：AC BD =；(2)用α表示AMB ∠的大小；(3)求证：OM 平分AMD ∠．【详解】（1）证明：AOB COD α∠=∠=，AOB BOC COD BOC ∴∠+∠=∠+∠，即AOC BOD ∠=∠，在AOC 和BOD 中，OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩，()SAS AOC BOD ∴≌， ∴AC BD =，（2）解：由三角形的外角性质得：AMB OBD OAC AOB ∠+∠=∠+∠，由（1）得()SAS AOC BOD ≌△△，∴OAC OBD ∠=∠，AMB AOB α∴∠=∠=，（3）证明：作OG AM ⊥于G ，OH DM ⊥于H ，如图所示，则90OGA OHB ∠=∠=︒，在OAG △和OBH △中，OGA OHB OAC OBDOA OB ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AAS OAG OBH ∴≌， OG OH ∴=，OG AM ⊥于G ，OH DM ⊥于H ，MO ∴平分AMD ∠，是ABC 的角平分线，且交于点(1)APB ∠=______．(2)求证：点P 在C ∠的平分线上．【详解】（1）解：证明：60C ∠=︒，AE ，BD 是ABC 的角平分线，12ABP ABC ∴∠=∠，12BAP BAC ∠=∠，11()(180)6022BAP ABP ABC BAC C ∴∠+∠=∠+∠=︒−∠=︒， 120APB ∴∠=︒；（2）如图，过P 作PF AB ⊥，PG AC ⊥，PH BC ⊥，AE ，BD 分别平分CAB ∠，CBA ∠，PF PG ∴=，PF PH =，PH PG ∴=，∴点P 在C ∠的平分线上；（3）如图，在AB 上取点M 使AM AD =，连接PM ，AE 是BAC ∠的平分线，PAM PAD ∴∠=∠， 在AMP 与ADP △中，AP AP PAM PADAM AD =⎧⎪∠=∠⎨⎪=⎩，()SAS AMP ADP ∴≌， 18060APM APD APB ∴∠=∠=︒−∠=︒，180()60BPM APM APD ∴∠=︒−∠+∠=︒，60BPE APD ∠=∠=︒，BPM BPE ∴∠=∠，BD Q 是ABC ∠的角平分线，MBP EBP ∴∠=∠，在BPM △与BPE 中，MBP EBP BP BPBPE BPM ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ASA BPM BPD ∴≌，BM BE ∴=， AB AM BM AD BE ∴=+=+． (1)如图1，连接AC BD ，，交点为G ，连接OG ，求证：①AC BD =；②OG 平分DGC ∠；(2)如图2，若90AOD BOC ∠=∠=︒，E 是CD 的中点，过点在同一条直线上．∴AOD AOB BOC AOB ∠+∠=∠+∠，∴AOB AOC ∠=∠，又∵OA OD =，OB OC =，∴()SAS DOB AOC V V ≌，∴AC BD =；②如图所示，过点O 作OH DB ⊥于点H ，OF AC ⊥于点F ，∵DOB AOC ≌，OH DB ⊥，OF AC ⊥∴OH OF =，∴点O 在DGC ∠的角平分线上，∴OG 是DGC ∠的角平分线，∴OG 平分DGC ∠；（2）证明：连接OE ，并延长到N ，使NE OE =，连接CN ，∵E 是CD 的中点，∴CE DE =，又∵CEN DEO ∠=∠，NE OE =，∴()SAS CEN DEO ∠V V ≌，∴NCE ODE ∠=∠，CN OD =，∴CN OD ∥，∴180OCN COD CN OA ∠+∠=︒=，，90AOD BOC ∠=∠=︒，180AOB COD ∴∠+∠=︒，OCN AOB ∴∠=∠，在ONC 和BAO 中，OC OB OCN AOBCN OA =⎧⎪∠=∠⎨⎪=⎩，()SAS ONC BAO ∴≌， NOC ABO ∴∠=∠，OF AB ⊥，90ABO BOF ∴∠+∠=︒，90NOC BOF ∴∠+∠=︒，180NOC BOF BOC ∴∠+∠+∠=︒，∴点E O F ，，在同一条直线上．题型四：尺规作图—作角平分线 例4．（2023春·陕西榆林·七年级校考期末）如图，已知ABC ，利用尺规，在AC 边上求作一点D ，使得ABD DBC ∠=∠.（保留作图痕迹，不写作法）【详解】解：如图点D 即为所求..【变式1】（2023春·福建福州·七年级福建省福州第十九中学校考期末）如图，Rt ABC △中，90BAC ∠=︒，AD 为BC 边上的高．(1)尺规作图，在AB 边上求作点P ，使得点P 到边BC 的距离等于AP （保留作图痕迹，不写做法）：(2)连接CP （P 为所求作的点）交AD 于点Q ，若30B ∠=︒，求AQC ∠的度数．【详解】（1）解：如图：点P 即为所求；作法：作ACB ∠的角平分线，与AB 的交点P 即为所求；理由：∵CP 是ACB ∠的角平分线，∴点P 到AC 的距离等于点P 到BC 的距离，∵90BAC ∠=︒，∴点P 到AC 的距离即为PA 的值，故点P 到边BC 的距离等于AP ．（2）解：如图：∵90BAC ∠=︒，30B ∠=︒，∴180903060ACB ∠=︒−−︒=︒，又∵AD 为BC 边上的高，∴90ADC ∠=︒，∴180906030DAC ∠=︒−−︒=︒，由（1）可知CP 是ACB ∠的角平分线， ∴1302ACQ QCD ACB ∠=∠=∠=︒，∴1803030128001ACQ DAC AQC ∠−∠=︒−︒−︒=︒∠=︒−． 【变式2】（2023·甘肃兰州·统考中考真题）综合与实践问题探究：（1）如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9：“平分一个已知角．”即：作一个已知角的平分线，如图2是欧几里得在《几何原本》中给出的角平分线作图法：在OA 和OB 上分别取点C 和D ，使得OC OD =，连接CD ，以CD 为边作等边三角形CDE ，则OE 就是AOB ∠的平分线．请写出OE 平分AOB ∠的依据：____________；类比迁移：（2）小明根据以上信息研究发现：CDE 不一定必须是等边三角形，只需CE DE =即可．他查阅资料：我国古代已经用角尺平分任意角．做法如下：如图3，在AOB ∠的边OA ，OB 上分别取OM ON =，移动角尺，使角尺两边相同刻度分别与点M ，N 重合，则过角尺顶点C 的射线OC 是AOB ∠的平分线，请说明此做法的理由；拓展实践：（3）小明将研究应用于实践．如图4，校园的两条小路AB 和AC ，汇聚形成了一个岔路口A ，现在学校要在两条小路之间安装一盏路灯E ，使得路灯照亮两条小路（两条小路一样亮），并且路灯E 到岔路口A 的距离和休息椅D 到岔路口A 的距离相等．试问路灯应该安装在哪个位置？请用不带刻度的直尺和圆规．．．．．．．．．．在对应的示意图5中作出路灯E 的位置．（保留作图痕迹，不写作法）【详解】解：（1）∵OC OD =，CE DE =，DE DE =，∴()SSS OCE ODE ≌，∴AOE BOE ∠=∠，∴OE 是AOB ∠的角平分线；故答案为：SSS（2）∵OM ON =，CM CN =，OC OC =，∴()SSS OCM OCN ≌，∴AOC BOC ∠=∠，∴OC 是AOB ∠的角平分线；（3）如图，点E 即为所求作的点；． 【变式3】（2023春·重庆九龙坡·七年级校考期末）如图，已知在ABC 中，90BAC ∠=︒，AD BC ⊥于点D ．（1）尺规作图：作ABC ∠的平分线交AC 于点E ，交AD 于点F ；（要求：保留作图痕迹，不写作法，不下结论）（2）在（1）的条件下，求证：AFE AEF ∠=∠．AD BC ⊥90ADB ∴∠=︒∴__________90BFD +∠=︒又BFD ∠=__________FBD ∴∠+__________90=︒90BAC ∠=︒ABF ∴∠+__________90=︒BF 平分ABC ∠ABF ∴∠=__________AFE AEF ∴∠=∠．【详解】（1）如图所示，（2）AD BC ⊥90ADB ∴∠=︒∴FBD ∠90BFD +∠=︒又BFD ∠=AEF ∠FBD ∴∠+AEF ∠90=︒90BAC ∠=︒ABF ∴∠+AFE ∠90=︒ BF 平分ABC ∠ABF ∴∠=FBD ∠AFE AEF ∴∠=∠．故答案为：FBD ∠；AEF ∠；AEF ∠；AFE ∠；FBD ∠．【过关检测】一、单选题 1．（2023春·四川泸州·八年级统考期末）如图，70AOB ∠=︒，点C 是AOB ∠内一点，CD OA ⊥于点D ，CE OB ⊥于点E ．且CD CE =，则DOC ∠的度数是（ ）A ．30︒B ．35︒C ．40︒D ．45︒【答案】B【分析】根据角平分线的判定定理可得OC 平分AOB ∠，再计算角度．【详解】解：∵CD OA ⊥，CE OB ⊥，CD CE =，∴OC 平分AOB ∠， ∴1352DOC AOB ∠=∠=︒，故选C ．【点睛】本题主要考查了角平分线的判定，注意：到角的两边距离相等的点在角平分线上． 2．（陕西省榆林市高新区2022-2023学年七年级下学期期末数学试题）如图，在Rt ABC △中，ABC ∠的平分线BD 交AC 于点D ，过点D 作DE AB ⊥交AB 于点E ．若9cm CD =，则点D 到AB 的距离是（ ）A ．9cmB ．6cmC ．4.5cmD ．3cm【答案】A 【分析】根据角平分线的性质，角平分线上的点到角两边的距离相等，即可求解．【详解】∵BD 平分ABC ∠，DE AB ⊥，AC BC ⊥，∴9DC DE ==，∴点D 到AB 的距离是9cm ．故选：A ．【点睛】本题考查角平分线的性质，解题的关键是掌握角平分线的性质．3．（2023春·河南焦作·七年级校考期末）如图，在四边形ABCD 中，90A ∠=︒，3AD =，连接BD ，BD CD ⊥，ADB C ∠=∠．若P 是BC 边上一动点，则DP 的长不可能是（ ）【答案】A【分析】根据余角的性质可得ABD CBD ∠=∠，即BD 平分ABC ∠，作DE BC ⊥于E ，则3AD DE ==，再根据垂线段最短即可得到答案．【详解】解：∵90A ∠=︒，BD CD ⊥，∴90,90ABD ADB CBD C ∠+∠=︒∠+∠=︒，∵ADB C ∠=∠，∴ABD CBD ∠=∠，即BD 平分ABC ∠，作DE BC ⊥于E ，则3AD DE ==，∵P 是BC 边上一动点，则DP DE ≥，即3DP ≥，∴DP 的长不可能是52；故选：A ．【点睛】本题考查了直角三角形的性质和角平分线的性质，得出BD 平分ABC ∠是解题的关键．A ．12∠=∠且CM DM =B ．13∠=∠且CM DM =C ．12∠=∠且OD DM =D ．23∠∠=且OD DM =【答案】A 【分析】由作图过程可得：,OD OC CM DM ==，再结合DM DM =可得()SSS COM DOM ≌，由全等三角形的性质可得12∠=∠即可解答．【详解】解：由作图过程可得：,OD OC CM DM ==，∵DM DM =，∴()SSS COM DOM ≌．∴12∠=∠．∴A 选项符合题意；不能确定OC CM =,则13∠=∠不一定成立，故B 选项不符合题意；不能确定OD DM =,故C 选项不符合题意，OD CM ∥不一定成立，则23∠∠=不一定成立，故D 选项不符合题意．故选A ．【点睛】本题主要考查了角平分线的尺规作图、全等三角形的判定与性质等知识点，理解尺规作图过程是解答本题的关键． ，ABC 的面积为，则ABC 的周长为（ A ．4B ．6C ．24D ．12【答案】C 【分析】过点E 作EF AB ⊥，垂足为F ，过点E 作EG AC ⊥，垂足为G ，根据角平分线的性质可得1EG EF ED ===，然后根据三角形的面积公式进行计算即可解答．【详解】解：过点E 作EF AB ⊥，垂足为F ，过点E 作EG AC ⊥，垂足为G ，∵BE 平分ABC ∠，ED BC ⊥，EF AB ⊥，∴1EF ED ==，∵CE 平分ACB ∠，ED BC ⊥，EG AC ⊥，∴1ED EG ==，∴ABC 的面积ABE =的面积BEC +△的面积AEC +△的面积()11111122222AB EF BC ED AC EG AB BC AC =⋅+⋅+⋅=⨯⨯++=，∴24AB BC AC ++=，即ABC 的周长为24．故选：C ．【点睛】本题考查了角平分线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．A ．3PD =B ．3PD <C ．3PD ≤ D ．3PD ≥【答案】D 【分析】根据角平分线的性质得到3PF =，再根据垂线段最短即可解答．【详解】解：过点P 作PE AB ⊥于点E ，过点P 作PF BC ⊥于点F ，∵点P 在ABC ∠的平分线上，∴PE PF =， ∵3PE =，∴3PF =，∴根据垂线段最短可知：3PD ≥，故选D ．【点睛】本题考查了角平分线的性质，垂线段最短，掌握角平分线的性质是解题的关键． 八年级统考期末）如图，在ABC 中， A ．83 B ．43 【答案】D【分析】由题意可求DC 的长，由角平分线的性质可求解．【详解】解：如图，过点D 作DH AB ⊥，垂足为H ，∵143AC DC AC ==，，∴1DC =，∵BD 平分ABC ∠，90C DH AB =︒∠，⊥，∴1CD DH ==，∴点D 到AB 的距离等于1，故选：D ．【点睛】本题考查了角平分线的性质，熟练运用角平分线的性质是本题的关键．8．（2023春·湖南娄底·八年级统考期末）如图，三条公路把A ，B ，C 三个村庄连成一个三角形区域，现决定在这个三角形区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，则这个集贸市场应建在（ ）A ．三角形三个内角的角平分线的交点B ．三角形三条边的垂直平分线的交点C ．三角形三条高的交点D ．三角形三条中线的交点【答案】A 【分析】根据角平分线上的点到角的两边的距离相等解答即可．【详解】解：根据角平分线的性质，集贸市场应建在三个角的角平分线的交点处．故选：A ．【点睛】本题主要考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．9．（2023春·陕西榆林·八年级统考期末）如图，OD 平分AOB ∠，DE AO ⊥于点E ，5DE =，F 是射线OB 上的任意一点，则DF 的长度不可能是（ ）【答案】A 【分析】过Ｄ点作DH OB ⊥于H ，根据角平分线的性质得5DH DE ==，再利用垂线段最短得到5DF ≥，然后对各个选项进行判断即可，【详解】过Ｄ点作DH OB ⊥于H ，OD 平分AOB ∠，DE OA ⊥，DH OB ⊥，5DH DE ∴==，DF DH ≥，5DF ∴≥，故选A【点睛】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等，也考查了垂线段最短，掌握角平分线的性质是解题的关键． 10．（2023春·河南开封·七年级统考期末）如图，在ABC 中，90C ∠=︒，AD 平分BAC ∠，DE AB ⊥于E ，则下列结论：①DE CD =；②AD 平分CDE ∠；③BAC BDE ∠=∠；④BE AC AB +=，其中正确的是（ ）A ．1个B ．2个C ．3个D ．4个【答案】D 【分析】①根据角平分线的性质得出结论：DE CD =；②证明ACD AED △≌△，得AD 平分CDE ∠；③由四边形的内角和为360︒得180CDE BAC ∠+∠=︒，再由平角的定义可得结论是正确的；④由ACD AED ∆≅∆得AC AE =，再由AB AE BE =+，得出结论是正确的．【详解】解：①90C ∠=︒，AD 平分BAC ∠，DE AB ⊥，DE CD ∴=；所以此选项结论正确；②DE CD =，AD AD =，90ACD AED ∠=∠=︒，ACD AED ∴≌，ADC ADE ∴∠=∠，AD ∴平分CDE ∠，所以此选项结论正确；③90ACD AED ∠=∠=︒，3609090180CDE BAC ∴∠+∠=︒−︒−︒=︒，180BDE CDE ∠+∠=︒，BAC BDE ∴∠=∠，所以此选项结论正确；④ACD AED ≌，AC AE ∴=，AB AE BE =+，BE AC AB ∴+=，所以此选项结论正确；本题正确的结论有4个，故选D ．【点睛】本题考查了全等三角形性质和判定，同时运用角平分线的性质得出两条垂线段相等；本题难度不大，关键是根据HL 证明两直角三角形全等，根据等量代换得出线段的和，并结合四边形的内角和与平角的定义得出角的关系．二、填空题 七年级统考期末）如图，在ABC 中，ABC 的内部相交于点 【答案】5【分析】先根据尺规作图描述得出AD 为BAC ∠的角平分线，再根据角平分线的性质得到点D 到AB 的距离5DE =，进而求出三角形的面积．【详解】由作法得AD 平分BAC ∠，如图所示，过点D 作DE AB ⊥于E ，∵90ACB ∠=︒，根据角平分线的性质，得43DC DE ==，ABD ∴的面积114102233AB DE AB =⋅⋅=⨯⨯=． ∴5AB =，故答案为：5．【点睛】本题考查角平分线的性质，解决本题的关键是熟知角平分线的性质并灵活应用．【答案】2【分析】根据尺规作图可得BF 平分ABC ∠，再利用角平分线的性质定理可得出2DF CF ==，最后根据垂线段最短即可得出FH 的最小值是2．【详解】解：如图，过点F 作FD AB ⊥于D ．由作图可知，BF 平分ABC ∠，∵FC BC ⊥，FD AB ⊥，∴2DF CF ==．根据垂线段最短可知，FH 的最小值为DF 的长，即为2．故答案为：2．【点睛】本题主要考查角平分线的性质，垂线段最短，解题的关键在于能够准确判断出BF 是ABC ∠的角平分线．13．（2023春·重庆沙坪坝·七年级重庆八中校考期末）如图，Rt ABC △中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ，E 为线段AC 上一点，连接DE ，且B CED ∠=∠．若16AB =，6CE =，则AE 的长为________．【答案】4【分析】过点D 作DF AB ⊥于点F ，由角平分线的性质得出DC DF =，证明DCE DFB ≌，得出BF CE =，求出AF ，由HL 证明Rt Rt ADC ADF ≌，得出AC AF =，即可求出结果．【详解】解：过点D 作DF AB ⊥于点F ，如图所示：∵90C ∠=︒，AD 平分BAC ∠交BC 于点D ，，∴DC DF =，在DCE △和DFB △中，90=BFD DCE B CEDDC DF ∠=∠=︒⎧⎪∠=∠⎨⎪⎩，∴()AAS DCE DFB ≌，∴6BF CE ==，∴10AF AB BF =−=，在Rt ADC 与Rt ADF 中，==DC DF AD AD ⎧⎨⎩，∴Rt Rt ADC ADF ≌，∴10AC AF ==，∴1064AE AC CE =−=−=．故答案为：4．【点睛】此题考查全等三角形的判定和性质和角平分线的性质，解题的关键是作出辅助线，构造全等三角形，根据HL 证明直角三角形的全等解答．【答案】30【分析】由作图可知OC 是AOB ∠的角平分线，根据角平分线的定义即可得到答案．【详解】解：由题意可知，OC 是AOB ∠的角平分线，∴11603022AOC AOB ∠=∠=⨯︒=︒．故答案为：30【点睛】此题考查角平分线的作图、角平分线相关计算，熟练掌握角平分线的作图是解题的关键．，则POD 的面积是【答案】6【分析】过点P 作PF OB ⊥交OB 于点F ，由作图可知OP 是AOB ∠的平分线，根据角平分线的性质得3PF PC ==，即可求得POD 的面积．【详解】解：如图，过点P 作PF OB ⊥交OB 于点F ，由作图可知，OP 是AOB ∠的平分线，∵PC OA ⊥，PF OB ⊥，∴3PF PC ==，∴POD 的面积为：162OD PF ⋅=，故答案为：6．【点睛】本题考查了尺规作角平分线以及角平分线的性质定理：角平分线上的点到角两边的距离相等．16．（2023春·山东泰安·七年级统考期末）如图，在锐角ABC 中，60BAC ∠=︒，BE 、CD 为ABC 的角平分线．且BE 、CD 交于点F ，连接AF ．有下列四个结论：①120BFC ∠=︒；②BD CE =；③BC BD CE =+；④FBD FEC FBC S S S +=△△△．其中结论正确的序号是__________ ．【答案】①③④【分析】根据角平分线的定义和三角形内角和定理求出BFC ∠；在BC 上取BM BD =，证明()SAS DBF MBF ≌△△，再证明()ASA MCF ECF ≌△△；过点F 作FG AB ⊥于点G ，FH AC ⊥于点H ，FK BC ⊥于点K ，根据角平分线的性质和三角形面积公式分别对各个结论进行判断即可．【详解】解：∵ABC 的两条角平分线BE 和CD 交于点F ，60BAC ∠=︒，∴FBC FCB∠+∠()12ABC ACB =∠+∠()11802BAC ︒=−∠()1180602=⨯︒−︒60=︒， ∴()180********BFC FBC FCB ∠=︒−∠+∠=︒−︒=︒，故结论①正确； ∴18060BFD BFC CFE Ð=°-Ð=°=Ð，在BC 上取BM BD =，∵BE 平分ABC ∠，∴DBF MBF Ð=Ð，在DBF 和MBF V 中，BD BM DBF MBFBF BF =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS DBF MBF ≌△△， ∴60BFD BFM ∠=∠=︒，∴1206060CFM BFC BFM ∠=∠−∠=︒−︒=︒，∴60CFM CFE ∠=∠=︒，∵CD 平分ACB ∠，∴MCF ECF ∠=∠，在MCF △和ECF △中，CFM CFE CF CFMCF ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴()ASA MCF ECF ≌△△， ∴CM CE =，∴BC BM CM BD CE =+=+，故结论③正确；∵没有条件得出点M 是BC 的中点，∴不能得出BD 与CE 一定相等，故结论②错误；过点F 作FG AB ⊥于点G ，FH AC ⊥于点H ，FK BC ⊥于点K ，∵BE 、CD 为ABC 的角平分线，∴FG FK =，FK FH =，∴FG FK FE ==， ∵12FBD S BD FG =⋅△，12FEC S EC FH =⋅△，12FBC S BC FK =⋅△，∴FBD FEC S S +△△1122BD FG EC FH =⋅+⋅ 1122BM FK MC FK =⋅+⋅ ()12BM MC FK =+⋅ 12BC FK =⋅FBC S =△，∴FBD FEC FBC S S S +=△△△，故结论④正确，∴结论正确的序号是①③④．故答案为：①③④．【点睛】本题考查角平分线的性质，全等三角形的判定与性质，三角形内角和定理，三角形的面积，作出辅助线构造全等三角形是解题的关键．三、解答题 17．（2023春·重庆江北·七年级统考期末）完成下面的解答过程，并填上适当的理由．已知：如图，DE BC ∥，BD 平分ABC ∠，EF 平分AED ∠．解： ∵DE BC ∥（已知）∴ABC AED ∠=∠（ ① ）．∵BD 平分ABC ∠，EF 平分∠∴112ABC ∠=∠，122AED ∠=∠【答案】两直线平行，同位角相等 2∠ 等量代换 同位角相等，两直线平行【分析】先分析角的位置关系，根据平行线的性质及判定定理，即可写出答案．【详解】证明：∵DE BC ∥（已知），∴ABC AED ∠=∠．∵BD 平分ABC ∠，EF 平分AED ∠，∴112ABC ∠=∠，122AED ∠=∠．∴12∠=∠（等量代换）．∴EF BD ∥（同位角相等，两直线平行）．故答案为：两直线平行，同位角相等 ； 2∠ ；等量代换 同位角相等，两直线平行．【点睛】本题主要考查平行线的性质（两直线平行，同位角相等），及平行线的判定方法（同位角相等，两直线平行）．牢记平行线的性质和判定方法是解题的关键．18．（2023春·山东泰安·七年级统考期末）如图，在AOB 和COD △中，OA OB =，OC OD =，OA OC <，36AOB COD ∠=∠=︒，连接AC 、BD 交于点M ，连接OM ．求证：(1)36AMB ∠=︒；(2)MO 平分AMD ∠．【答案】(1)证明见解析 (2)证明见解析【分析】（1）证明()SAS AOC BOD ≌△△，由三角形全等的性质得出OAC OBD ∠=∠，由三角形的外角性质得：AMB OBD OAC AOB ∠+∠=∠+∠，可得出AMB ∠的度数；（2）作OG AC ⊥于G ，OH BD ⊥于H ，利用全等三角形对应边上的高相等，得出OG OH =，由角平分线的判定方法即可得证．【详解】（1）证明：∵36AOB COD ∠=∠=︒，∴AOB BOC COD BOC ∠+∠=∠+∠，即AOC BOD ∠=∠，在AOC 和BOD 中，OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS AOC BOD ≌△△， ∴OAC OBD ∠=∠，∵AEB ∠是AOE △和BME 的外角∴AEB AMB OBD AOB OAC ∠=∠+∠=∠+∠，∴36AMB AOB ∠=∠=︒；（2）如图所示，作OG AC ⊥于G ，OH BD ⊥于H ，∴OG 是AOC 中AC 边上的高，OH 是BOD 中BD 边上的高，由（1）知：AOC BOD ≌，∴OG OH =，∴点O 在AMD ∠的平分线上，即MO 平分AMD ∠．【点睛】本题考查全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识．证明三角形全等是解题的关键． 七年级统考期末）如图，在ABC 中， (2)18【分析】（1）根据BD 平分ABC ∠，CD 平分ACB ∠得12DBC ABC ∠=∠，12DCB ACB ∠=∠，根据40ABC ∠=︒，70ACB ∠=︒得140202DBC ∠=⨯︒=︒，170352DCB ∠=⨯︒=︒，根据三角形内角和定理即可得；（2）过点D 作DF BC ⊥于点F ，根据BD 平分ABC ∠，DE AB ⊥，DF BC ⊥得DE DF =，根据4DE =得4DF =，即可得．【详解】（1）解：∵BD 平分ABC ∠，CD 平分ACB ∠，∴12DBC ABC ∠=∠，12DCB ACB ∠=∠，∵40ABC ∠=︒，70ACB ∠=︒，∴140202DBC ∠=⨯︒=︒，170352DCB ∠=⨯︒=︒，∴在BCD △中，1802035125BDC ∠=︒−︒−︒=︒；（2）解：过点D 作DF BC ⊥于点F ，∵BD 平分ABC ∠，DE AB ⊥，DF BC ⊥，∴DE DF =，∵4DE =，∴4DF =，∵9BC =， ∴11S 941822BCD BC DF =⨯⨯=⨯⨯=△．【点睛】本题考查了角平分线，三角形内角和定理，三角形的面积，解题的关键是理解题意，掌握这些知识点． 八年级假期作业）如图，在ABC 中， 【答案】6cm CD =，34B ∠=︒【分析】根据角平分线的性质可得CD DE =，28BAD CAD ∠=∠=︒，再根据直角三角形的两个锐角互余即可求出B ∠的度数．【详解】解：∵ABC 中，90C ∠=︒，AD 平分BAC ∠，DE AB ⊥，∴6cm CD DE ==，28BAD CAD ∠=∠=︒，∴256BAC CAD ∠=∠=︒，∴9034B CAD ∠=︒−∠=︒．【点睛】本题考查了角平分线的性质定理和直角三角形的两个锐角互余，属于基础题型，熟练掌握角平分线的点到一个角的两边距离相等是解题关键．21．（2023春·广西南宁·七年级南宁十四中校考期末）如图，已知ABC ．(1)尺规作图：作BAC ∠的角平分线交BC 于点G （不写作法，保留作图痕迹）；(2)如果6AB =，10AC =，ABG 的面积为18，求ACG 的面积．【答案】(1)见解析(2)30【分析】（1）根据角平分线的尺规作图方法作图即可；（2）如图所示，过点G 作GE AB GF AC ⊥⊥，垂足分别为E 、F ，证明AEF AFG △≌△，得到EG FG =，根据面积法求出6EG FG ==，再根据三角形面积公式求解即可．【详解】（1）解：如图所示：（2）解：如图所示，过点G 作GE AB GF AC ⊥⊥，垂足分别为E 、F ，∴90AEG AFG ∠=∠=︒，∵AG 是BAC ∠的角平分线，∴EAG FAG ∠=∠，又∵AG AG =，∴()AAS AEF AFG △≌△，∴EG FG =；∵6AB =，ABG 的面积为18，∴1182AB EG ⋅=，即16182EG ⨯=，∴6EG =，∴6EG FG ==，∴111063022ACG S AC FG =⋅=⨯⨯=△．【点睛】本题主要考查了全等三角形的性质与判定，三角形面积，角平分线的尺规作图，角平分线的定义等等，灵活运用所学知识是解题的关键． 22．（2023春·山西太原·七年级统考期末）如图，在ABC 中，AD 是它的角平分线，DE AB ⊥于点,E DF AC ⊥于点F ，且BE CF =．线段BD 与CD 相等吗？说明理由．【答案】BD CD =，见解析【分析】根据角平分线的性质得出DE DF =，根据垂直定义得出90DEB DFC ∠=∠=︒，根据SAS 证明DFC △D E B ≌△，得出BD CD =即可．【详解】解：BD CD =；理由如下：∵AD 是BAC ∠的角平分线，DE AB ⊥，DF AC ⊥，∴DE DF =，∵DE AB ⊥，DF AC ⊥，∴90DEB DFC ∠=∠=︒，又∵BE CF =，∴DFC △DE B ≌△， ∴BD CD =．【点睛】本题主要考查了角平分线的性质，垂线定义理解，三角形全等的判定和性质，解题的关键是熟练掌握三角形全等的判定方法，证明DFC △DE B ≌△． 23．（重庆市大渡口区2022-2023学年七年级下学期期末数学试题）如图，AD BC ∥，180B BCD ∠+∠=︒．(1)用直尺和圆规完成以下基本作图：过点A 作BAD ∠的角平分线，交CD 于点F ，与BC 的延长线交于点E ；（不写做法，保留作图痕迹）(2)求证：CFE FEC ∠=∠．证明：∵AD BC ∥（已知），∴DAF FEC ∠=∠（①__________）． ∵AE 平分BAD ∠，∴②__________（角平分线的定义）． ∴BAE FEC ∠=∠（③__________）． ∵180B BCD ∠+∠=︒（已知）， ∴④__________（⑤__________）． ∴BAE CFE ∠=∠（两直线平行，同位角相等）． ∴CFE FEC ∠=∠（等量代换）． 【答案】(1)见解析(2)见解析【分析】（1）利用基本作图作BAD ∠的平分线即可；（2）先根据平行线的性质得到DAF FEC ∠=∠，再利用角平分线的定义得到BAE DAF ∠=∠，则BAE FEC ∠=∠，接着证明AB CD ∥得到BAE CFE ∠=∠，然后利用等量代换得到CFE FEC ∠=∠．【详解】（1）解：如图，BE 为所作；（2）证明：AD BC ∥（已知）， DAF FEC ∴∠=∠（两直线平行，内错角相等）．AE 平分BAD ∠，BAE DAF ∴∠=∠（角平分线的定义），BAE FEC ∴∠=∠（等量代换）．180B BCD ∠+∠=︒（已知），AB CD ∴∥（同旁内角互补，两直线平行）．BAE CFE ∴∠=∠（两直线平行，同位角相等）．CFE FEC ∴∠=∠（等量代换）．【点睛】本题考查了作图−基本作图：熟练掌握5种基本作图是解决问题的关键．也考查了角平分线的性质和平行线的判定与性质． 七年级校考阶段练习）如图，ABC 中， 若BCG 的面积为，则ABC 的面积为【答案】(1)120︒(2)3(3)6【分析】（1）根据作图方法可得BG 是ABC ∠的角平分线，则1302ABG ABC ==︒∠∠，再由三角形外角的性质可得120BGC A ABG =+=︒∠∠；（2）如图所示，过点G 作GD BC ⊥于D ，先求出3AG AC CG =−=，再证明ABG DBG △≌△，得到3DG AG ==，根据垂线段最短可知线段H G 的最小值为3；（3）证明BDG CDG △≌△，得到122BDG CDG BCG S S S ===△△△，进而求出2BDG ABG S S ==△△，则6ABC ABG CBG S S S =+=△△△．【详解】（1）解：由作图方法可知BG 是ABC ∠的角平分线， ∴1302ABG ABC ==︒∠∠，∵90A ∠=︒，∴120BGC A ABG =+=︒∠∠，故答案为：120︒；（2）解：如图所示，过点G 作GD BC ⊥于D ，∴90BAG BDG ==︒∠∠，∵96AC CG ==，，∴3AG AC CG =−=，∵BG 是ABC ∠的角平分线，∴ABG DBG ∠=∠，又∵BG BG =，∴()AAS ABG DBG △≌△，∴3DG AG ==，∵H 是边BC 上一动点，∴当点H 与点D 重合时，HG 最小，∴线段HG 的最小值为3， 故答案为：3；（3）解：∵BG 是ABC ∠的角平分线，∴30ABG DBG ==︒∠∠，∵9030C ABC ∠=︒−∠=︒，∴GBD C ∠=∠，又∵90DG DG BDG CDG ===︒，∠∠，∴()AAS BDG CDG △≌△， ∴122BDG CDG BCG S S S ===△△△，∵ABG DBG △≌△，∴2BDG ABG S S ==△△，∴6ABC ABG CBG S S S =+=△△△，故答案为：6．【点睛】本题主要考查了全等三角形的性质与判定，三角形内角和定理，三角形外角的性质，角平分线的定义，角平分线的尺规作图等等，正确作出辅助线构造全等三角形是解题的关键． 七年级统考期末）ABC 中， (2)如图2，若ABC 是锐角三角形．过点FED ∠，EDB ∠与ABC ∠ (3)若ABC 是钝角三角形，其中FED ∠，EDB ∠与ABC ∠之间的数量关系．【答案】(1)45 (2)12BDE FED ABC ∠=∠+∠，证明见解析 (3)12ABC BDE DEF ∠=∠+∠【分析】（1）首先证明AED ABC ∠=∠得到DE BC ∥，得到EDB DBC ∠=∠，再根据角平分线的定义得到1452DBC ABC ∠=∠=︒，即可证明；（2）延长ED 、BC 交于G ，利用平行线的性质得FED G ∠=∠，再利用三角形外角的性质可得结论；（3）由（2）同理解决问题．【详解】（1）解：DE AB ∵⊥，90AED ∴∠=︒．90ABC ∠=︒，AED ABC ∴∠=∠．DE BC ∴∥．EDB DBC ∴∠=∠．BD Q 平分ABC ∠，1452DBC ABC ∴∠=∠=︒．45EDB ∴∠=︒．（2）如图，12BDE FED ABC ∠=∠+∠，理由如下：延长ED 、BC 交于G ，EF BC ∥，FED G ∴∠=∠，BD Q 平分ABC ∠，。

第12讲角的概念与大小比较知识定位讲解用时：5分钟A、适用范围：人教版初一，基础一般；B、知识点概述：本讲义主要用于人教版初一新课，主要学习角的概念与大小比较，掌握角的概念及角的表示方法，并能进行角度的互换；能借助三角尺画一些特殊角，掌握角大小的比较方法；会利用角平分线的意义进行有关表示或计算；掌握角的和、差、倍、分关系，并会进行有关计算.知识梳理讲解用时：15分钟角的定义及其表示方法(1)角的定义：有公共端点的两条射线组成的图形叫做角，这个公共端点是角的顶点，这两条射线是角的两条边．角也可以看作是由一条射线绕着它的端点旋转而形成的图形．当终边和始边成一条直线时，形成等角；当终边和始边重合时，形成周角．(2)角的表示方法：有四种表示角的方法：①用一个阿拉伯数字表示单独的一个角，在角内用一段弧标注；②用一个大写英文字母表示单独的一个角，当角的顶点处有两个或两个以上的角时，不能用这种方法表示角；③用一个小写希腊字母表示单独的一个角；④用三个大写英文字母表示任意一个角，这时表示顶点的字母一定要写在中间．角的理解(1)角的大小与边的长短无关，只与构成角的两条射线张开的幅度大小有关，角可以度量，可以比较大小，可以进行运算；(2)如果没有特别说明，所说的角都是指小于平角的角．1.角度制：以度、分、秒为单位的角的度量制，叫做角度制．2.角度的换算：角的度量单位是度、分、秒，把一个周角360等分，每一份就是1度的角，记作1°；把1度的角60等分，每一份就是1分的角，记作1′；把1分的角60等分，每一份就是1秒的角，记作1″.角度的换算(1)度、分、秒的换算是60进制，与时间中的时、分、秒的换算相同； (2)角的度数的换算有两种方法：①由度化成度、分、秒的形式(即从高位向低位化)，用乘法，1°＝60′， 1′＝60″；①由度、分、秒化成度的形式(即从低位向高位化),1″⎝ ⎛⎭⎪⎫＝160′，1′⎝ ⎛⎭⎪⎫＝160°，用除法．注意：度及度、分、秒之间的转化必须逐级进行转化，“越级”转化容易出错．1.角的比较： （1）度量法：用量角器量出角的度数，然后按照度数比较角的大小，度数大的角大，度数小的角小；反之，角大度数大，角小度数小． （2）叠合法：把两个角的顶点和一边分别重合，另一边放在重合边的同旁，通过另一边的位置关系比较大小． 技巧 角的比较 ①在度量法中，注意三点：对中、重合、度数；②在叠合法中，要注意顶点重合，一边重合，另一边落在重合这边的同侧．2.角的和差：角的和、差有两种意义，几何意义和代数意义．几何意义对于今后读图形语言有很大帮助，代数意义是今后角的运算的基础．①几何意义：如图所示，①AOB与①BOC的和是①AOC，表示为①AOB＋①BOC＝①AOC；①AOC与①BOC的差为①AOB，表示为①AOC－①BOC＝①AOB.①代数意义：如已知①A＝23°17′，①B＝40°50′，①A＋①B就可以像代数加减法一样计算，即①A＋①B＝23°17′＋40°50′＝64°7′，①B－①A＝40°50′－23°17′＝17°33′.3.角的平分线：从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线．如图所示，射线OC是①AOB的平分线，则有①1＝①2＝12①AOB或①AOB＝2①1＝2①2.角的平分线的理解角的平分线是一条射线，不是线段，也不是直线，它必须满足下面的条件：①是从角的顶点引出的射线，且在角的内部；②把已知角分成了两个角，且这两个角相等．课堂精讲精练【例题1】（1）在∠AOB内部画1条射线OC，则图1中有个不同的角；（2）在∠AOB内部画2条射线OC，OD，则图2中有个不同的角；（3）在∠AOB内部画3条射线OC，OD，OE，则图3中有个不同的角；【答案】（1）3；（2）6；（3）10．【解析】解：（1）在①AOB内部画1条射线OC，则图中有3个不同的角，故答案为：3．（2）在①AOB内部画2条射线OC，OD，则图中有6个不同的角，故答案为：6．（3）在①AOB内部画3条射线OC，OD，OE，则图中有10个不同的角，故答案为：10．讲解用时：5分钟解题思路：根据角的概念，结合图形，即可数出角的个数．教学建议：考查了角的有关概念的应用难度： 3 适应场景：当堂例题例题来源：无【练习1.1】如图所示，下列表示角的方法错误的是（）A．∠1与∠AOB表示同一个角B．∠β表示的是∠BOCC．图中共有三个角：∠AOB，∠AOC，∠BOCD．∠AOC也可用∠O来表示【答案】D．【解析】解：A、∠1与∠AOB表示同一个角，正确，故本选项错误；B、∠β表示的是∠BOC，正确，故本选项错误；C、图中共有三个角：∠AOB，∠AOC，∠BOC，正确，故本选项错误；D、∠AOC不能用∠O表示，错误，故本选项正确；故选：D．讲解用时：3分钟解题思路：根据角的表示方法表示各个角，再判断即可．教学建议：本题考查了对角的表示方法的应用，主要检查学生能否正确表示角．难度： 3 适应场景：当堂练习例题来源：无【例题2】(1)将70.23°用度、分、秒表示；(2)将26°48′36″用度表示．【答案】（1）70°13′48″；(2)26.81°.【解析】解：(1)将0.23°化为分，可得0.23×60′＝13.8′，再把0.8′化为秒，得0.8×60″＝48″.所以70.23°＝70°13′48″.(2)把36″化成分，36″＝')601(×36＝0.6′，48′＋0.6′＝48.6′，把48.6′化成度，48.6′＝︒⎪⎭⎫ ⎝⎛601×48.6＝0.81°. 所以26°48′36″＝26.81°.讲解用时：6分钟解题思路：：(1)70.23°实际是70°＋0.23°，这里70°不要变，只要将0.23°化为分，然后再把所得的分中的小数部分化为秒．将0.23°化为分，只要用0.23乘以60′即可．(2)将26°48′36″用度表示，应先将36″化成分，然后再将分化成度就可以了．将36″化成分，可以用')601(乘以36. 教学建议：要求学生熟练掌握度、分、秒的换算难度： 3 适应场景：当堂例题 例题来源：无【练习2.1】若∠A=20°18′，∠B=20°15′30〞，∠C=20.25°，则（ ）A ．∠A ＞∠B ＞∠C B ．∠B ＞∠A ＞∠CC ．∠A ＞∠C ＞∠BD ．∠C ＞∠A ＞∠B【答案】A ．【解析】解：∵∠A=20°18′，∠B=20°15′30〞，∠C=20.25°=20°15′，∴∠A＞∠B＞∠C．故选A．讲解用时：5分钟解题思路：∠A、∠B已经是度、分、秒的形式，只要将∠C化为度、分、秒的形式，即可比较大小．教学建议：两个角比较大小．在比较时要注意统一单位后再比较．难度： 3 适应场景：当堂练习例题来源：无【练习2.2】3.76°=度分秒；22°32′24″=度．【答案】3、45、36、22.54．【解析】解：3.76°=3度45分36秒；22°32′24″=22.54度．故填3、45、36、22.54．讲解用时：5分钟解题思路：此类题是进行度、分、秒的转化运算，相对比较简单，注意以60为进制．教学建议：进行度、分、秒的转化运算，注意以60为进制．难度： 3 适应场景：当堂练习例题来源：无计算：18°13′×5﹣49°28′52″÷4【答案】78°42′47′′【解析】解：原式=90°65′﹣48°88′52′′÷4=90°65′﹣12°22′13′′=78°42′47′′讲解用时：6分钟解题思路：根据度分秒的除法，从大的单位算起，余数乘以进率化成小的单位再除，可得答案．教学建议：要求学生熟练掌握度、分、秒的换算难度： 3 适应场景：当堂例题例题来源：无【练习3.1】计算：77°53′26″+33.3°=．【答案】111°11′26″．【解析】解：77°53′26″+33.3°=77°53′26″+33°18′=110°71′26″=111°11′26″．故答案为：111°11′26″．讲解用时：5分钟解题思路：先将33.3°转化为33°18′，然后度与度、分与分、秒和秒对应相加，秒的结果满60转化为分，分的结果满60转化为度．教学建议：度分秒的换算，注意以60为进制难度： 3 适应场景：当堂例题例题来源：无如图，数一数以O为顶点且小于180°的角一共有多少个？你能得到解这类问题的一般方法吗？【答案】28个；一般方法为：（n﹣1）+（n﹣2）+…+2+1=．【解析】解：7+6+5+4+3+2+1==28，一般地如果MOG小于180，且图中一共有n条射线，则小于180°的角一共有：（n﹣1）+（n﹣2）+…+2+1=．讲解用时：5分钟解题思路：先根据题意算出以O为顶点且小于180°的角一共有7+6+5+4+3+2+1=28个，然后根据第一问的解法得出一般方法为：（n﹣1）+（n﹣2）+…+2+1=．教学建议：考查角的大小比较，结合图找出符合条件的角，从而推出解这类问题的一般方法．难度： 3 适应场景：当堂例题例题来源：无如图所示，其中最大的角是，∠DOC，∠DOB，∠DOA的大小关系是．【答案】∠AOD，∠DOA＞∠DOB＞∠DOC．【解析】解：由图可知，最大的角是∠AOD；∠DOA＞∠DOB＞∠DOC．故答案为：∠AOD，∠DOA＞∠DOB＞∠DOC．讲解用时：5分钟解题思路：根据图形，结合角的概念与大小比较的方法：度量法和覆盖法，即可得出结论．教学建议：熟悉角的大小比较的两种方法：度量法和覆盖法．难度： 3 适应场景：当堂练习例题来源：无【例题5】如图，∠AOB=120°，OC是∠AOB内部任意一条射线，OD、OE分别是∠AOC、∠BOC的角平分线，下列叙述正确的是（）A．∠DOE的度数不能确定B．∠AOD=∠EOCC．∠AOD+∠BOE=60°D．∠BOE=2∠COD【答案】C．【解析】解：A、∵OD、OE分别是∠AOC、∠BOC的平分线，∴∠DOE=（∠BOC+∠AOC）=∠AOB=60°．故本选项叙述错误；B、∵OD是∠AOC的角平分线，∴∠AOD=∠AOC．又∵OC是∠AOB内部任意一条射线，∴∠AOC=∠EOC不一定成立．故本选项叙述错误；C、∵OD、OE分别是∠AOC、∠BOC的平分线，∴∠BOE+∠AOD=∠EOC+∠DOC=∠DOE=（∠BOC+∠AOC）=∠AOB=60°．故本选项叙述正确；D、∵OC是∠AOB内部任意一条射线，∴∠BOE=∠AOC不一定成立，∴∠BOE=2∠COD不一定成立．故本选项叙述错误；故选：C．讲解用时：5分钟解题思路：本题是对角的平分线的性质的考查，角平分线将角分成相等的两部分．结合选项得出正确结论．教学建议：根据角平分线定义得出所求角与已知角的关系转化求解．难度： 3 适应场景：当堂例题例题来源：无【练习5.1】如图，下列条件中不能确定的是OC是∠AOB的平分线的是①．∠AOC=∠BOC②．∠AOB=2∠AOC③．∠AOC+∠BOC=∠AOB④．【答案】①②④．【解析】解：①、∠AOC=∠BOC能确定OC平分∠AOB，正确；②、∠AOB=2∠AOC能确定OC平分∠AOB，正确；③、∠AOC+∠COB=∠AOB不能确定OC平分∠AOB，错误；④、∠BOC=∠AOB，能确定OC平分∠AOB，错误．故正确答案为：①②④．讲解用时：8分钟解题思路：直接利用角平分线的性质分别分析得出答案．教学建议: 正确把握角平分线的定义是解题关键．难度： 3 适应场景：当堂练习例题来源：无【例题6】已知∠AOB=60°，其角平分线为OM，∠BOC=20°，其角平分线为ON，求∠MON 的大小【答案】20°或40°．【解析】解：∠BOC在∠AOB内部∵∠AOB=60°，其角平分线为OM∴∠MOB=30°∵∠BOC=20°，其角平分线为ON∴∠BON=10°∴∠MON=∠MOB﹣∠BON=30°﹣10°=20°；∠BOC在∠AOB外部∵∠AOB=60°，其角平分线为OM∴∠MOB=30°∵∠BOC=20°，其角平分线为ON∴∠BON=10°∴∠MON=∠MOB+∠BON=30°+10°=40°．讲解用时：10分钟解题思路：根据题意，画出图形，分两种情况讨论：∠BOC在∠AOB内部和外部．教学建议：考查平分线的性质，注意引导学生分类讨论难度： 3 适应场景：当堂例题例题来源：无【练习6.1】已知∠AOB=70°，∠BOC=20°，OE为∠AOB的平分线，OF为∠BOC的平分线，则∠EOF=．【答案】25°或45°．【解析】解：（1）当点C在∠AOB的内部时，∠EOF=∠AOB﹣∠BOC=35°﹣10°=25°；（2）当点C在∠AOB的外部时，∠EOF=∠AOB+∠BOC=35°+10°=45°．故答案为25°或45°．讲解用时：5分钟解题思路：此题分点C在∠AOB的内部和外部两种情况讨论．教学建议：查角平分线的定义，重点是分类讨论．难度： 3 适应场景：当堂练习例题来源：无如图，已知∠BOC=2∠AOB，OD平分∠AOC，∠BOD=14°，求∠AOB的度数．【答案】28°．【解析】解：设∠AOB=x，∠BOC=2x．则∠AOC=3x．又OD平分∠AOC，∴∠AOD=x．∴∠BOD=∠AOD﹣∠AOB=x﹣x=14°∴x=28°即∠AOB=28°．讲解用时：5分钟解题思路：此题可以设∠AOB=x，∠BOC=2x，再进一步表示∠AOC=3x，根据角平分线的概念表示∠AOD，最后根据已知角的度数列方程即可计算．教学建议：考查角平分线的定义．此类题设恰当的未知数，根据已知条件进一步表示出相关的角，列方程计算．难度： 3 适应场景：当堂例题例题来源：无如图，已知O是直线AB上一点，∠1=20°，OD平分∠BOC，则∠2的度数是度．【答案】80【解析】解：如图，∵∠1=20°，∠1+∠BOC=180°，∴∠BOC=160°．又∵OD平分∠BOC，∴∠2=∠BOC=80°；故填：80．讲解用时：6分钟解题思路：首先根据平角角的定义得到∠BOC=160°；然后由角平分线的定义求得∠2=∠BOC．教学建议：注意此题中隐含着已知条件：∠1+∠BOC=180°．难度： 3 适应场景：当堂练习例题来源：无如图所示，∠AOB：∠BOC：∠COD=4：5：3，OM平分∠AOD，∠BOM=20°，求∠AOD和∠MOC．【答案】∠AOD=120°，∠MOC=30°．【解析】解：设∠AOB=4x，∠BOC=5x，∠COD=3x，∴∠AOD=12x，∵OM平分∠AOD，∴∠AOM=∠AOD=6x，由题意得，6x﹣4x=20°，解得，x=10°，∴∠AOD=12x=120°，∠BOC=5x=50°，∴∠MOC=∠BOC﹣∠BOM=30°．讲解用时：8分钟解题思路：设∠AOB=4x，∠BOC=5x，∠COD=3x，得到∠AOD=12x，根据角平分线的定义得到∠AOM=∠AOD=6x，根据题意列出方程，解方程即可．教学建议：掌握设未知数求解角度的方法，可类比应用题的求解方式.难度： 3 适应场景：当堂例题例题来源：无如图，已知OB是∠AOC的平分线，OD是∠COE的平分线，如果∠AOE=140°，∠BOC比∠COD的2倍还多10°，那么∠AOB是多少度？【答案】50度【解析】解：设∠COD的度数为x，∵OD是∠COE的平分线，∴∠EOC=2∠COD=2x，∵∠BOC比∠COD的2倍还多10°，∴∠BOC=2x+10°，∵OB是∠AOC的平分线，∴∠AOB=∠BOC，∠AOC=2∠BOC=4x+20°，∵∠AOE=140°，∴2x+4x+20°=140°，解得x=20°，∴∠BOC=2x+10°=50°∴∠AOB是50度．讲解用时：8分钟解题思路：设∠COD的度数为x，则∠BOC=2x+10°，利用角平分线定义得到∠EOC=2∠COD=2x，∠BOC=2x+10°，再利用OB是∠AOC的平分线得到∠AOB=∠BOC，∠AOC=2∠BOC=4x+20°，所以2x+4x+20°=140°，解得x=20°，然后计算2x+10°即可．教学建议:理解角平分线的定义：灵活应用角平分线的定义进行角度的计算．难度： 3 适应场景：当堂练习例题来源：无课后作业【作业1】如图，点D在∠AOB的内部，点E在∠AOB的外部，点F在射线OA上，试比较下列各角的大小．（1）∠AOB∠BOD；（2）∠AOE∠AOB；（3）∠BOD∠FOB；（4）∠AOB∠FOB；（5）∠DOE∠BOD．【答案】（1）＞；（2）＞；（3）＜；（4）=；（5）＞．【解析】解：（1）∠AOB＞∠BOD；（2）∠AOE＞∠AOB；（3）∠BOD＜∠FOB；（4）∠AOB=∠FOB；（5）∠DOE＞∠BOD．讲解用时：2分钟难度： 2 适应场景：练习题例题来源：无A BC D O 【作业2】如图，已知AOB DOC ∠=∠，56AOC ∠=︒，DOB ∠=______．【答案】56°．【解析】解：由题可知：56DOB DOC COB AOB COB AOC ∠=∠+∠=∠+∠=∠=． 讲解用时：3分钟难度： 3 适应场景：练习题 例题来源：无【作业3】如图所示，已知点O 在直线AB 上，∠AOE ：∠EOD=1：3，OC 是∠BOD 的平分线，∠EOC=115°，求∠AOE 和∠BOC ．【答案】①AOE=25°，①BOC=40°．【解析】解：∵∠AOE：∠EOD=1：3，∴设∠AOE=x，则∠EOD=3x，又∵∠EOC=115°，∴∠COD=115°﹣3x，∵OC是∠BOD的平分线，∴∠COB=∠COD=115°﹣3x，又∵点O在直线AB上，∴∠AOE+∠EOD+∠COD+∠COB=180°，∴x+3x+2（115﹣3x）=180°，解得，x=25°，∴∠AOE=25°，∴∠BOC=115°﹣3×25°=40°．讲解用时：8分钟难度： 3 适应场景：练习题例题来源：无。

因为∠AOC＝30°，射线 OG 将∠BOC 分为 1∶4 两部分，所以∠BOC ＝150°，∠COG＝30°，∠BOG＝120°由(1)知∠BOD＝60°，所以∠DOG ＝∠BOG－∠BOD＝120°－60°＝60°；
②当射线 OG 位于 DB 之间时，如图②所示，因为∠AOC＝30°，射线 OG 将∠BOC 分为 1∶4 两部分，所以∠BOC＝150°，∠COG＝120°，∠ BOG＝30°，由(1)知∠BOD＝60°，所以∠DOG＝∠BOD－∠BOG＝60° －30°＝30°
6. 经过 E、F、G 三点画直线 , 可以画__D__条.
A. 1
B. 2 C. 3 D. 1 或 3
解 : 如下图.
E
F
G
EFG
7. 以下图形中有线段、射线或直线 , 根据它们 的基本特征可判断出 , 其中能够相交的有〔 B 〕
ab
a b
①a、b为直线
b
a
②a为线段，b 为直线
b
a
③a为线段、b为射线
这时 AM = BM = 1 AB 2
或 AB = 2AM = 2BM.
角的定义
角由两条具有公共端点的射线组成 , 两条射 线的公共端点是这个角的顶点.
边
顶点
边
角也可以看成是由一条射线绕着它的端 点旋转而成的.
终边
O
始边
角的表示
B 1
α
A
C
∠BAC 或 ∠A
∠α
∠1
角的度量 1°的 1 为 1 分，记作 1′，即 1°= 60′. 60 1′ 的 1 为 1 秒，记作 1′′，即 1′ = 60′′. 60 1 平角 = 180° 1 周角 = 360°

3．线段的长短比较： (1)线段长短比较的实质是线段的长度的比较． (2)线段长短的比较方法：
①度量法(数)：用刻度尺量出线段的长度，根据长度大小来比较， 长度大的线段较长，长度相等时两线段相等． ②叠合法(形)：比较两条线段AB与CD的长短，可以把线段AB移 到线段CD上，使点A与点C重合，点B与点D在重合点的同一侧．
3．(1)两点的所有连线中，__线__段_最__短______．简单说成： __两__点__之_间__，__线__段__最_短____________．
(2)连接两点的线段的长度，叫作这两点间的___距__离____．
例1.如图，已知线段a、b，尺规作图：
(1)画一条线段AC＝a＋b；(根据下列作法画出图形)
知识点4：线段的中点及等分点(难点)
1．线段的中点：如图，点M在线段AB上，AM＝BM，点M叫作线 段AB的中点.
应用：因为点M是线段AB的中点，所以AM＝BM＝
1 2
AB，
AB＝2AM＝2BM.
2．线段的等分点：
如图①所示，B，C是线段AD上的两点，
且AB＝BC＝CD＝
1 3
AD或AD＝3AB＝3BC＝3CD，
活动导入
同学们，请你在草稿纸上画一条线段AB. 你能在草稿纸上作出一条同样大小的线段吗？ 你是怎么做的？
情境导入 同学们，请你们观察这三组图形，你能比较出每组图形中线段a和b 的长短吗？
a b
事实上，这三组图形中，线段a和b的长度是相等的. 很多时候，眼见未必为实，准确比较线段的长短还 需要更加严谨的办法.
小组展示
越展越优秀
提疑惑：你有什么疑惑？
知识点1：线段的画法及长短比较(重点)
1．尺规作图：在数学中，我们常限定用无刻度的直尺和圆规作图， 这就是尺规作图．

专题12.9角平分线的性质（知识梳理与考点分类讲解）第一部分【知识点归纳】【知识点一】角的平分线的性质(1)性质：角的平分线上的点到角两边的距离相等.(2)符号语言：OC平分∠ADB，又 PE⊥AD，PF⊥BD，垂足为E、F，∴PE=PF【知识点二】角的平分线的判定(1)判定：角的内部到角两边距离相等的点在角的平分线上.(2)符号语言：PE⊥AD，PF⊥BD，垂足为E、F，又 PE=PF∴OC平分∠ADB，【知识点三】角的平分线的尺规作图（1）以O 为圆心，适当长为半径画弧，交OA 于D，交OB 于E.（2）分别以D、E 为圆心，大于12DE 的长为半径画弧，两弧在∠AOB 内部交于点C.（3）画射线OC.射线OC 即为所求.第二部分【题型展示与方法点拨】【题型1】利用角平分线性质定理进行求值与证明【例1】（23-24七年级下·山东菏泽·阶段练习）如图，在ABC 中，90ACB ∠=︒，CD AB ⊥于点D ，BE 平分ABC ∠交AC 于点E ，交CD 于点F ，过点E 作EG CD ∥，交AB 于点G ，连接CG ．（1）求证：90A AEG ∠+∠=︒；（2）求证：EC EG =；【分析】本题考查了角平分线的性质，平行线的性质，垂直的定义，解题的关键是灵活运用所学知识解决问题．（1）证明90EGA ∠=︒，即可证明结论成立；（2）利用角平分线性质定理即可证明结论成立．（1）证明：∵CD AB ⊥，∴90CDA ∠=︒EG CD ∥，∴90EGA CDA ∠=∠=︒∵180A AEG EGA ∠+∠+∠=︒1801809090A AEG EGA ∴∠+∠=︒-∠=︒-︒=︒（2）证明：∵90ACB ∠=︒，∴EC BC⊥BE 平分ABC ∠，EG AB ⊥，EC EG∴=【变式1】（23-24七年级下·广东佛山·阶段练习）如图，OC 平分AOB ∠，点P 是射线OC 上一点，PM OB ⊥交于点M ，点N 是射线OA 上的一个动点，连接PN ．若6PM =，则PN 的长度不可能是（）A ．18B ．7.2C ．6D ．4.5【答案】D 【分析】本题考查角平分线的性质、垂线段最短，根据角平分线的性质作出图形转化线段是解决问题的关键．过点P 作PD OA ⊥，如图所示，由角平分线的性质可得6PD PM ==，根据点与直线上各点的距离中垂线段最短可得6PN PD ≥=，从而得到答案．解：过点P 作PD OA ⊥，如图所示：OC 平分AOB ∠，点P 是射线OC 上一点，PM OB ⊥于点M ，6PM =，∴由角平分线性质可得6PD PM ==，点N 射线OA 上的一个动点，连接PN ，∴由点与直线上各点的距离中垂线段最短可得6PN PD ≥=，∴综合四个选项可知，PN 的长度不可能是4.5，故选：D ．【变式2】（23-24七年级下·四川巴中·期末）如图，在ABC 中，ABC ∠，ACB ∠的平分线交于点O ，点O 到BC 边的距离为3，且ABC 的周长为20，则ABC 的面积为．【答案】30【分析】本题考查角平分线的性质、三角形的面积公式，熟练掌握角平分线的性质是解答的关键．过O 作OM AB ⊥于M ，ON AC ⊥于N ，连接OA ，利用角平分线的性质求得3OM ON OD ===，然后利用ABC AOB AOC BOC S S S S =++ 求解即可．解：过O 作OM AB ⊥于M ，ON AC ⊥于N ，连接OA ，∵点O 到BC 边的距离为3，∴3OD =，∵ABC 的周长为20，∴20AB AC BC ++=∵ABC ∠，ACB ∠的平分线交于点O ，OM AB ⊥，ON AC ⊥，∴3OM ON OD ===，∴ABC AOB AOC BOCS S S S =++ 111222AB OM AC ON BC OD =⋅+⋅+⋅()12AB AC BC OD =++⋅12032=⨯⨯30=，故答案为：30．【题型2】利用角平分线判定定理进行求值与证明【例2】如图，DE AB ⊥于E DF AC ⊥，于F ，若BD CD BE CF ==、，（1）求证：AD 平分BAC ∠；（2）已知204，==AC BE ，求AB 的长．【答案】(1)见详解(2)12【分析】本题考查了全等三角形的性质和判定的应用，注意：全等三角形的判定定理有,,,SAS ASA AAS SSS ，全等三角形的对应边相等，对应角相等．（1）求出90E DFC ∠=∠=︒，根据全等三角形的判定定理得出Rt BED Rt CFD ≌，推出DE DF =，根据角平分线性质得出即可；（2）根据全等三角形的性质得出,==AE AF BE CF ，即可求出答案．（1）证明：∵,DE AB DF AC ⊥⊥，∴90E DFC ∠=∠=︒，∴在Rt BED 和Rt CFD 中，BD CD BE CF =⎧⎨=⎩，∴()Rt BED Rt CFD HL ≌，∴DE DF =，∵,DE AB DF AC ⊥⊥，∴AD 平分BAC ∠；（2）解：∵90,,∠=∠=︒==AED AFD AD AD DE DF ，∴()Rt ADE Rt ADF HL ≌，∴AE AF =，∵20,4===AC CF BE ，∴20416AE AF ==-=，∴16412AB AE BE =-=-=．【变式1】如图，在ABC 中，70BAC ∠=︒，4AB =，2AC =，若2ABD ACD S S = ，则CAD ∠的度数为（）A ．45︒B ．40︒C ．35︒D ．30︒【答案】C 【分析】作DE AB ⊥于点E ，作DF AC ⊥于点F ，根据2ABD ACD S S = 可证DE DF =，从而可知AD 是BAC∠的平分线，进而可求出CAD ∠的度数．解：如图，作DE AB ⊥于点E ，作DF AC ⊥于点F ，∵2ABD ACD S S = ，∴11222AB DE AC DF ⋅=⨯⋅．∵4AB =，2AC =，∴44DE DF=∴DE DF =，∴AD 是BAC ∠的平分线．∴11703522CAD BAC ∠=∠=⨯︒=︒．故选C ．【变式2】6．（23-24八年级上·山东聊城·阶段练习）如图，在ABC 中，48ABC ∠=︒，三角形的外角DAC ∠和ACF ∠的平分线交于点E ，则EBF ∠=．【答案】24︒【分析】本题考查了角平分线的性质和角平分线的定义，解题的关键是能正确作出辅助线，证明BE 平分ABC ∠；过点E 作EM AB EN BC EO AC ⊥⊥⊥、、，根据角平分线的性质可得EM EO EN EO ==，，则有EM EN =，再根据EM AB EN BC ⊥⊥、，即可得出BE 平分ABC ∠即可解答．解：过点E 作EM AB EN BC EO AC ⊥⊥⊥、、，如图所示：三角形的外角DAC ∠和ACF ∠的平分线交于点E ，EM EO EN EO ∴==，，EM EN ∴=，EM AB EN BC ⊥⊥、，∴BE 平分ABC ∠，11482422EBF ABC ∴∠==⨯︒=︒，故答案为：24︒．【题型3】综合运用角平分线性质定理与判定定理进行证明与求值【例3】如图，ABC 和EBD △中，90ABC DBE AB CB BE BD ∠=∠=︒==，，，连接AE CD AE ，，与CD 交于点M ，AE 与BC 交于点N ．（1）求证：AE CD =；（2）求证：AE CD ⊥；（3）连接BM ，有以下两个结论：①BM 平分CBE ∠；②MB 平分AMD ∠，其中正确的一个是（请写序号），并给出证明过程．【答案】(1)见详解(2)见详解(3)②【分析】本题考查全等三角形的判定和性质、等腰直角三角形的性质、角平分线的判定与性质定理等知识，解题的关键是正确寻找全等三角形解决问题，学会添加常用辅助线解决问题．（1）欲证明AE CD =，只要证明ABE CBD ≌；（2）由ABE CBD ≌，推出BAE BCD ∠=∠，由180NMC BCD CNM ∠=︒-∠-∠，18090ABC BAE ANB CNM ANB ABC ∠=︒-∠-∠∠=∠∠=︒，又，，可得90NMC ∠=︒；（3）结论：②；作BK AE ⊥于K BJ CD ⊥，于J ．利用角平分线的判定定理证明即可．（1）证明：∵ABC DBE ∠=∠，∴ABC CBE DBE CBE ∠+∠=∠+∠，即ABE CBD ∠=∠，在ABE 和CBD △中，AB CB ABE CBD BE BD =⎧⎪∠=∠⎨⎪=⎩，∴SAS ABE CBD ≌（），∴AE CD =．（2）证明：∵ABE CBD ≌，∴BAE BCD ∠=∠，∵180180NMC BCD CNM ABC BAE ANB ∠=︒-∠-∠∠=︒-∠-∠，，又CNM ANB ∠=∠，90ABC ∠=︒ ，∴90NMC ∠=︒，∴AE CD ⊥．（3）解：结论：②理由：作BK AE ⊥于K BJ CD ⊥，于J．∵ABE CBD ≌，∴ABE CDB AE CD S S == ，，∴1122AE BK CD BJ ⨯⨯=⨯•，∴BK BJ =，∵作BK AE ⊥于K ，BJ CD ⊥于J ，∴BM AMD ∠平分．不妨设①成立，则CBM EBM ≌，则AB BD =，显然不可能，故①错误．故答案为：②．【变式1】（23-24八年级上·浙江杭州·阶段练习）如图，90B C ∠=∠=︒，M 是BC 的中点，DM 平分ADC ∠，且100ADC ∠=︒，则MAB ∠的度数是（）A ．50︒B ．40︒C ．45︒D ．55︒【答案】B 【分析】本题考查了角平分线的性质和判定，解题的关键是掌握角平分线上的点到两边距离相等．作MN AD ⊥于N ，根据角平分线的性质得出MN MC =，进而得出1402MAB DAB ∠=∠=︒．解：作MN AD ⊥于N ，∵90B C ∠∠==︒，∴AB CD ∥，∴18080DAB ADC ∠∠=︒-=︒，∵DM 平分ADC ∠，MN AD ⊥，MC CD ⊥，∴MN MC =，∵M 是BC 的中点，∴MC MB =，∴MN MB =，又MN AD ⊥，MB AB ⊥，∴1402MAB DAB ∠=∠=︒，故选：B ．【变式2】（23-24八年级上·重庆永川·期末）如图，在ABC 中，68BAC ∠=︒，72ACB ∠=︒，ACB ∠的平分线与BAC ∠的外角平分线交于点D ，连接BD ，则BDC ∠的大小等于．【答案】34︒/34度【分析】本题考查了角平分线的判定与性质，三角形外角的性质等知识，先根据角平分线的判定与性质得出BD 平分ABH ∠，然后利用三角形外角的性质12BDC DBH DCB BAC ∠=∠-∠=∠，即可求解．解：过点D 作DH BC ⊥于H ，DE AC ⊥于E ，DF AB ⊥于F ，∵ACB ∠的平分线与BAC ∠的外角平分线交于点D ，∴DE DF DH ==，12BCD ACB ∠=∠，∴BD 平分ABH ∠，∴12DBH ABH ∠=∠，∵68BAC ∠=︒，∴BDC DBH DCB ∠=∠-∠1122ABH ACB =∠-∠()12ABH ACB =∠-∠12BAC =∠1682=⨯︒34=︒，故答案为：34︒．【题型4】通过作图（作角平分线）进行求值或证明【例4】（23-24八年级上·广东珠海·期中）请回答下列问题：（1）如图1，已知ABC ，利用直尺和圆规，作BAC ∠的平分线AD 交BC 于点D （保留作图痕迹，不要求写作法）；（2）如图2所示，AD 是ABC 的角平分线E F 、分别是AB AC 、上的点，且180EDF BAC ∠+∠=︒，求证：DE DF =．【分析】（1）根据角平分线的基本作图方法作图即可；（2）过点D 作DH AB ⊥于点H ，作DQ AC ⊥于点Q ，证明()AAS EHD FQD ≌，得出DE DF =，即可得出答案．（1）解：如图，作BAC ∠的平分线AD 交BC 于点D ；（2）证明：如图，过点D 作DH AB ⊥于点H ，作DQ AC ⊥于点Q ，则90EHD FQD ∠=∠=︒，AD 平分BAC ∠，DH DQ ∴=，180EDF BAC ∠+∠=︒Q ，180AED AFD ∴∠+∠=︒，180DFQ AFD ∠+∠=︒ ，DEH DFQ ∴∠=∠，在EHD △和FQD △中DEH DFQ EHD FQD DH DQ ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AAS EHD FQD ∴ ≌，DE DF ∴=．【点拨】本题主要考查了角平分线的基本作图，角平分线的性质，三角形全等的判定和性质，补角的性质，解题的关键作图辅助线，熟练掌握三角形全等的判定方法．【变式1】（2024·湖南湘西·模拟预测）如图，在ABC 中，90C ∠=︒，以A 为圆心，任意长为半径画弧，分别交AC AB 、于点M ，N ，再分别以M ，N 为圆心，大于12MN 长为半径画弧，两弧交于点O ，作射线AO ，交BC 于点E ．已知4CE =，7AB =，ABE 的面积为（）A ．6B ．11C ．14D ．28【答案】C 【分析】此题考查了角平分线的性质定理，根据角平分线的性质得到点E 到AC 和AB 的距离相等，点E 到AB 的距离等于EC 的长度，利用三角形面积公式即可得到答案．解：由基本作图得到AE 平分BAC ∠，∴点E 到AC 和AB 的距离相等，∴点E 到AB 的距离等于EC 的长度，即点E 到AB 的距离为4，∴174142ABE S =⨯⨯= ．故选：C ．【变式2】（2024·湖南·中考真题）如图，在锐角三角形ABC 中，AD 是边BC 上的高，在BA ，BC 上分别截取线段BE ，BF ，使BE BF =；分别以点E ，F 为圆心，大于12EF 的长为半径画弧，在ABC ∠内，两弧交于点P ，作射线BP ，交AD 于点M ，过点M 作MN AB ⊥于点N ．若2MN =，4AD MD =，则AM =．【答案】6【分析】本题考查了尺规作图，角平分线的性质等知识，根据作图可知BP 平分ABC ∠，根据角平分线的性质可知2DM MN ==，结合4AD MD =求出AD ，AM ．解：作图可知BP 平分ABC ∠，∵AD 是边BC 上的高，MN AB ⊥，2MN =，∴2MD MN ==，∵4AD MD =，∴8AD =，∴6AM AD MD =-=，故答案为：6．第三部分【中考链接与拓展延伸】1、直通中考【例1】1．（2024·天津·中考真题）如图，Rt ABC △中，90,40C B ∠=︒∠=︒，以点A 为圆心，适当长为半径画弧，交AB 于点E ，交AC 于点F ；再分别以点,E F 为圆心，大于12EF 的长为半径画弧，两弧（所在圆的半径相等）在BAC ∠的内部相交于点P ；画射线AP ，与BC 相交于点D ，则ADC ∠的大小为（）A ．60B ．65C ．70D ．75【答案】B 【分析】本题主要考查基本作图，直角三角形两锐角互余以及三角形外角的性质，由直角三角形两锐角互余可求出50BAC ∠=︒，由作图得25BAD ∠=︒，由三角形的外角的性质可得65ADC ∠=︒，故可得答案解：∵90,40C B ∠=︒∠=︒，∴90904050BAC B ∠=︒-∠=︒-︒=︒，由作图知，AP 平分BAC ∠，∴11502522BAD BAC ∠=∠==︒⨯︒，又,ADC B BAD ∠=∠+∠∴402565,ADC ∠=︒+︒=︒故选：B【例2】．（2021·黑龙江大庆·中考真题）已知，如图1，若AD 是ABC 中BAC ∠的内角平分线，通过证明可得=AB BD AC CD，同理，若AE 是ABC 中BAC ∠的外角平分线，通过探究也有类似的性质．请你根据上述信息，求解如下问题：如图2，在ABC 中，2,3,BD CD AD ==是ABC 的内角平分线，则ABC 的BC 边上的中线长l 的取值范围是【答案】12522l <<【分析】根据题意得到2=3AB AC ，设AB ＝2k ，AC ＝3k ，在△ABC 中，由三边关系可求出k 的范围，反向延长中线AE 至F ，使得AE EF =，连接CF ，最后根据三角形三边关系解题．解：如图，反向延长中线AE 至F ，使得AE EF =，连接CF ，2,3,BD CD AD == 是ABC 的内角平分线，2==3AB BD AC CD ∴可设AB ＝2k ，AC ＝3k ，在△ABC 中，BC ＝5，∴5k ＞5，k ＜5，∴1＜k ＜5，BE EC AEB CEF AE EF =⎧⎪∠=∠⎨⎪=⎩()ABE FCE SAS ∴≅ AB CF∴=由三角形三边关系可知，AC CF AF AC CF-<<+5k AF k∴<<522k k AE ∴<<∴12522l <<故答案为：12522l <<．【点拨】本题考查角平分线的性质、中线的性质、全等三角形的判定与性质、三角形三边关系等知识，是重要考点，难度一般，掌握相关知识是解题关键．2、拓展延伸【例1】（23-24七年级下·重庆沙坪坝·阶段练习）如图1，在ABC 中，BD 为AC 边上的高，BF 是ABD ∠的角平分线，点E 为AF 上一点，连接AE ，45AEF ∠=︒．（1）求证：AE 平分BAF∠（2）如图2，连接CE 交BD 于点G ，若BAE 与CAE 的面积相等，求证：BG CF=【分析】本题主要考查了全等三角形的证明以及性质运用，角平分线的判定以及基本性质，熟练掌握全等三角形的几种判定方法以及角平分线的判定是解答该题的关键．（1）根据BF 是ABD ∠的角平分线和，BD 为AC 边上的高，可得114522BAD ABD ∠=︒-∠，由45AEF ∠=︒得145452BAE ABE ABD ∠=︒-∠=︒-∠，即可证明12BAE BAD ∠=∠；（2）过点E 作EM AB ⊥于点M ，EN AC ⊥于点N ，由角平分线性质可以得EM EN =，由BAE 与CAE 的面积相等可得AB AC =，证明(SAS)ABE ACE △≌△，得出135AEB CEB ∠=∠=︒，BE EC =，即可得出36090BEG CEF AEB AEC ∠=∠=︒-∠-∠=︒，再根据垂直模型证明ASA BEG CEF ≌（），即可得出结论．（1）证明：∵BD 为AC 边上的高，即90ADB ∠=︒，∴90ABD BAD ∠+∠=︒，∴1()452ABD BAD ∠+∠=︒，∴114522BAD ABD ∠=︒-∵45AEF ABF BAE ∠=∠+∠=︒，∴45BAE ABF ∠=︒-∠，∵12ABF ABD ∠=∠，∴1452BAE ABD ∠=︒-∠，∴12BAE BAF ∠=∠，即：AE 平分BAF ∠．（2）过点E 作EM AB ⊥于点M ，EN AC ⊥于点N ，AE 平分BAC ∠，且EM AB ⊥，EN AC ⊥，EM EN ∴=．ABE ACE S S △△＝，AB AC ∴=，AE 平分BAC ∠，BAE CAE ∴∠=∠，在ABE 和ACE △中，AB BC BAE CAE AE AE =⎧⎪∠=∠⎨⎪=⎩(SAS)ABE ACE ∴ ≌，AEB CEB ∴∠=∠，BE EC =，45AEF ∠=︒ ，135AEB AEC ∴∠=∠=︒，36090BEG CEF AEB AEC ∴∠=∠=︒-∠-∠=︒，BD 为AC 边上的高，90ADB ∴∠=︒，FBD BFC BFC FCE ∴∠+∠=∠+∠，EBG ECF ∴∠=∠．在BEG 和CEF △中，BEG CEF BE CE EBG ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩ASA BEG CEF ∴ ≌（）．BG CF ∴=.【例2】（23-24八年级上·江西宜春·期末）课本再现：思考如图12.3-3，任意作一个角AOB ∠，作出AOB ∠的平分线OC ．在OC 上任取一点P ，过点P 画出OA ，OB 的垂线，分别记垂足为D 、E ，测量PD 、PE 并作比较，你得到什么结论？在OC 上再取几个点试一试．通过以上测量，你发现了角的平分线的什么性质？【实验猜想】针对以上问题，同学们进行了小组实验探究，并猜想：角的平分线上的点到角的两边的距离相等．【推理证明】为了证明该定理，小明同学根据书上的图形（如图12.3-3）写出了“已知”和“求证”，请你利．．．用全等的知识完成证明过程．．．．．．．．．．．．．（1）已知：点P 是AOB ∠的平分线OC 上一点，过点P 作PD OA ⊥于点D ，PE OB ⊥于点E ．求证：PD PE =．【知识应用】（2）如图2，BAC ∠的平分线与ABC 的外角BCD ∠的平分线相交于点O ，过点O 作OD AC⊥于点D ，OE AB ⊥于点E ，连接OB ．①证明：OB 平分CBE ∠；②若70CAB ∠=︒，则COB ∠=________．【答案】（1）证明见解析（2）①证明见解析；②55︒【分析】（1）根据条件证明OPD OPE ≌V V ，从而PD PE =．（2）①过点O 作OF CB ⊥于点F ，由（1）的结论易证OD OF OE ==，根据“到角的两边距离相等的点在这个角的平分线上”得到OB 平分CBE ∠；②根据三角形的内角和180COB BCO CBO ∠=︒-∠-∠，再利用角平分线的定义和“三角形的一个外角等于不相邻的两个内角的和”，推导出1902COB BAC ∠=︒-∠，从而求解．（1）证明：OC 平分AOB ∠，AOC BOC ∴∠=∠，PD OA ⊥ ，PE OB ⊥，90ODP OEP ∴∠=∠=︒，在OPD △和OPE 中，AOC BOC ODP OPE OP OP ∠=∠⎧⎪∠=∠⎨⎪=⎩，OPD OPE ∴V V ≌，PD PE ∴=；（2）①证明：过点O 作OF CB ⊥于点F，AO 是ABC ∠的平分线，OD AC ⊥，OE AB ⊥，OD OE ∴=，CO 是BCD ∠的平分线，OD AC ⊥，OF BC ⊥，OD OF ∴=，OF OE ∴=，OF BC ⊥ ，OE AB ⊥，BO ∴平分CBE ∠，②OB Q 平分CBE ∠，OC 平分BCD ∠，12CBO CBE ∴∠=∠，12BCO BCD ∠=∠，()111180180180222COB CBO BCO CBE BCD CBE BCD ∴∠=︒-∠-∠=︒-∠-∠=︒-∠+∠()()11118018018090222CAB ACB CAB ABC CAB CAB =︒-∠+∠+∠+∠=︒-︒+∠=︒-∠19070552=︒-⨯︒=︒．故答案为：55︒．【点拨】本题考查了全等三角形的判定与性质、角平分线的定义、角平分线的性质和判定以及三角形的内角和定理、三角形外角的性质等，熟练掌握相关知识是解题的关键．。

第31讲 角的比较知识点01 角的大小比较方法1：度量比较法．先用量角器量出角的度数，然后比较它们的大小．方法2：叠合比较法．把其中的一个角移到另一个角上作比较．如比较∠AOB 和∠A′O′B′的大小： 如下图，由图（1）可得∠AOB<∠A′O′B′；由图(2)可得∠AOB=∠A′O′B′；由图(3)可得∠AOB>∠A′O′B′．知识点02 角的和、差关系如图所示，∠AOB 是∠1与∠2的和，记作：∠AOB=∠1+∠2；∠1是∠AOB 与∠2的差，记作：∠1=∠AOB-∠2．【说明】（1）用量角器量角和画角的一般步骤：①对中(角的顶点与量角器的中心对齐)；②重合(一边与刻度尺上的零度线重合)；③读数(读出另一边所在线的度数)．（2）利用三角板除了可以做出30°、45°、60°、90°外，根据角的和、差关系，还可以画出15°，75°，105°，120°，135°，150°，165°的角．知识点03 角平分线从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线．如图所示，OC 是∠AOB 的角平分线，∠AOB=2∠AOC=2∠BOC ，∠AOC=∠BOC =∠AOB ．12知识点04余角和补角（1）定义：一般地，如果两个角的和等于90°(直角)，就说这两个角互为余角，即其中一个角是另一个角的余角．类似地，如果两个角的和等于180°(平角)，就说这两个角互为补角，即其中一个角是另一个角的补角．（2）性质：（1）同角（等角）的余角相等．（2）同角（等角）的补角相等．已知13736'Ð=°，237.36Ð=°，则1Ð与2Ð的大小关系为（）A ．12ÐÐ<B ．12Ð=ÐC ．12ÐÐ>D ．无法比较若12515¢Ð=°，2251330¢¢¢Ð=°，325.35Ð=°，则（）A ．312Ð>Ð>ÐB ．213Ð>Ð>ÐC ．132Ð>Ð>ÐD ．123Ð>Ð>Ð如果124.12Ð=°，22412¢Ð=°，则∠1与∠2的大小关系是（）A ．12＜ÐÐB ．12＞ÐÐC ．12Ð=ÐD ．无法确定若3218A ¢Ð=°，321530B ¢¢¢Ð=°，32.25C Ð=°，则（）A ．ABC >>∠∠∠B ．B A CÐ>Ð>ÐC ．A C BÐ>Ð>ÐD ．C A B Ð>Ð>Ð在ÐAOB 的内部任取一点C ，作射线OC 那么有（）A ．ÐAOC=ÐBOCB ．ÐAOC >ÐBOCC ．ÐBOC >ÐAOBD ．ÐAOB >ÐAOC如图，∠AOC=∠BOD ，那么（）A ．∠AOD>∠BOCB ．∠AOD=∠BOC C ．∠AOD<∠BOCD ．两角关系不能确定如图，比较下列各角的度数，用“>”或“<”填空：考点精析考点一 角的大小比较∠AOC_____∠AOB ，∠BOD_____∠COD ，∠AOC_____∠AOD ，∠BOD_____∠BOC ．如图，若∠AOB=∠BOC ，则（）A ．∠COD>∠AOB B ．∠AOB>∠CODC ．∠AOB=∠COD D ．∠AOB 与∠COD 的大小不能确定如图，射线OC 、OD 分别在AOB Ð的内部外部，下列各式中错误的是（）A ．AOB AOD Ð<ÐB ．BOC AOBÐ<ÐC ．COD AODÐ>ÐD ．AOD AOC Ð>Ð如图，正方形网格中有∠α和∠β，则∠α与∠β的大小关系为（）A ．∠α<∠βB ．∠α=∠βC ．∠α>∠βD ．无法判断如图所示的网格是正方形网格，DEF Ð_____ABC Ð（填“>”，“=”或“<”）考点二 余角与补角已知∠α=25°30'，则它的补角为（）A ．25°30′B ．64°30'C ．164°30'D ．154°30′已知3540a Ð=°¢，则a Ð的补角的度数为（）A ．B ．C ．D ．若5317A ¢Ð=°，则A Ð的余角的度数为（）A ．B ．C ．D ．若a Ð与b Ð互余，且3a b Ð=Ð，则=Ðb （）A ．B ．C ．D ．若一个角的补角比它余角的2倍大，则这个角的度数为 ．一个角的余角比它的补角的13多12°，则这个角为 ．一个角比它的补角的13少40°，这个角等于 ．如果1Ð与2Ð互余，2Ð与3Ð互补，则1Ð与3Ð的关系是（）A ．B ．C ．D ．一个角的补角比这个角的余角的3倍小20°，则这个角的度数是 ．一个角比它的补角的13少40°，这个角等于 ．已知一个角的余角比它的补角的还少，求这个角．5560°¢5520°¢14460°¢14420°¢3643¢°4643¢°3617¢°4617¢°2230¢°2250¢°25°45°45°13Ð=Ð1390Ð=Ð-°1390Ð=Ð+°13270Ð+Ð=°495°考点三 角平分线类型一 角平分线（1）如图，OM 平分∠AOB ，下列说法错误的是（ ）A ．∠AOB =2∠AOM B ．∠AOM =∠BOMC ．∠AOM =2∠BOMD ．∠AOM =21∠AOB 如图，OB 平分AOD Ð，OC 平分BOD Ð，那么下列各式正确的是______．（多选）A ．AOD AOC Ð=Ð32B ．14BOC AODÐ=ÐC．12BOD AOD Ð=ÐD ．13BOD AODÐ=Ð已知三条不同的射线OA 、OB 、OC ，有下列条件，其中能确定OC 平分∠AOB 的有（）①∠AOC =∠BOC ；②∠AOB =2∠AOC ；③∠AOC +∠COB =∠AOB ；④∠BOC=21∠AOB.A ．1个B ．2个C ．3个D ．4个如图，∠EOC =4∠COD ,∠COD =20°，OE 为∠AOD 的平分线，求∠AOD 的大小，请补全解题过程．解：∵∠EOC =4∠COD ，∠COD =20°，∴∠EOC =________°，∴∠DOE =∠EOC −∠COD =_______°，∵OE 平分∠AOD ，则∠AOD =2∠________=120°．如图，直线、相交于，，是的角平分线，，求的度数．AB CD O 90EOC Ð=°OF AOE Ð34COF Ð=°BODÐ解：，（已知），　56　．是的角平分线， （角平分线的性质）． ． ，， ．如图所示，∠AOB =100°，OC 是∠AOB 内部的一条射线，射线OM 平分∠AOC ，射线ON 平分∠BOC ，求∠MON 的度数．解：因为射线，分别平分∠和∠，所以∠NOB =∠NOC = ∠BOC ，∠AOM =∠COM =∠AOC ，所以∠MON =∠ +∠ ===°已知：如图，∠AOB =40°，∠BOC =60°，OD 平分∠AOC ，求∠BOD 的度数．解：∵∠AOC =∠AOB +∠ ，又∵∠AOB =40°，∠BOC =60°，∴∠AOC = °．∵OD 平分∠AOC ，∴∠AOD =12∠AOC （ 　）．90EOC Ð=°Q 34COF Ð=°EOF \Ð=°OF Q AOE ÐAOF \Ð=56=°AOC \Ð=°AOC Ð+Q 90=°90BOD EOB Ð+Ð=°BOD AOC \Ð=Ð=(°)∴∠AOD =50°．∴∠BOD =∠AOD ﹣∠ ．∴∠BOD = °．如图所示，点O 是直线AB 上一点，OE ，OF 分别平分∠AOC 和∠BOC ，若∠AOC =68°，则∠BOF 和∠EOF 是多少度？如图，OB 为AOC Ð的平分线，OD 是COE Ð的平分线．（1）若40AOB Ð=°，30DOE Ð=°，求BOD Ð为多少度？（2）若AOE m Ð=°，COD n Ð=°，求AOB Ð为多少度？如图，O 为直线 AB 上一点，OM 平分∠AOC ，ON 平分∠BOC ， 则图中互余的角有_____对．如图，OB 是AOC Ð的平分线，OD 是COE Ð的平分线，150Ð=°AOE ，40AOB Ð=°．求AODÐ的度数．类型二 角平分线（2）如图，已知∠AOB =160°，OD 是∠AOB 内一条射线，OE 平分∠AOD ，OC 平分∠BO D ．（1）若∠AOE =55°，求∠EOC 的度数；（2）若∠BOC =19°，求∠EOD 的度数．如图，OB 是AOC Ð的平分线，OD 是COE Ð的平分线．（1）若30AOB Ð=°，20DOE Ð=°，那么BOD Ð是多少度？（2）若150AOE Ð=°，40AOB Ð=°，那么COD Ð是多少度？考点四 三角板中的角度计算类型一 三角板中的角度计算（1）将一副三角板按如图所示的方式放置，则∠ACD 的度数为（ ）A ．45°B ．60°C ．75°D ．80°如图，将一副三角尺的两个直角项点O 按如图方式叠放在一起，若∠AOC =130°，则∠BOD =（）A ．45°B ．50°C ．55°D ．60°如图，将一副三角板叠在一起，使它们的直角顶点O 重合，若∠AOB =165°，则∠COD 的度数为______．如图，直角三角板的直角顶点A 在直线l 上，如果∠1=35°，那么∠2的度数是（）A ．55°B ．45°C ．35°D ．25°如图，将一副三角板叠在一起，使它们的直角顶点重合于O 点，已知∠AOB =160°，则∠COD 的度数为（）A ．20°B ．30°C ．40°D ．50°如图，是一副三角板的摆放图，将一个三角板60°的角的顶点与另一个三角板的直角顶点重合，20BAE Ð=°，则CAD Ð的大小是（ ）A ．60°B ．50°C ．40°D ．30°将一副三角尺按如图所示的方式放置，∠BOC =35°，∠AOD 的度数是_____．如图，将两个三角尺的直角AOB Ð与COD Ð顶点O 重合在一起，若4AOD BOC Ð=Ð，OE 为BOC Ð的平分线，则DOE Ð的度数为（）A ．36°B ．45°C ．60°D ．72°一副三角板如图叠放，已知∠OAB =∠OCD =90°，∠AOB =45°，∠COD =60°，OB 平分∠COD ，则∠AOC =_____度．类型二 三角板中的角度计算（2）如图1，直角三角板COD 的直角顶点O 在直线AB 上，线段,OC OD 是三角板的两条直角边，射线OE 是AOD Ð的平分线．（1）当30COE Ð=°时，求BOD Ð的度数；（2）当COE a Ð=时，则BOD Ð=________（用含a 的式子表示）；（3）当三角板绕点O 逆时针旋转到图2位置时，BOD a Ð=，它条件不变，则BOD Ð=________（用含a 的式子表示）如图1所示，将两块直角三角尺的直角顶点C 叠放在一起．（1）若∠DCE =25°，则∠ACB =________°；若∠ACB =130°，则∠DCE =_________°．（2）如图2所示，若两个同样的三角板，将60°锐角的顶点A 叠放在一起，则∠DAB 与∠CAE 有何数量关系，请说明理由．（3）如图3所示，已知∠AOB =a ，∠COD =b （a ，b 都是锐角）．若把它们的顶点O 叠放在一起，将∠AOD 与∠BOC 的数量关系用含a 与b的式子表示出来，直接写出结论．如图，将两块三角板的直角顶点重合．（1）写出以C 为顶点的所有相等的角．（2）若148ACB Ð=°，求∠DCE 的度数．（3）猜想：∠ACB 与∠DCE 之间的数量关系为________．如图，以直线AB 上一点O 为端点作射线OC ，使∠BOC =70°，将一块直角三角板DOE 直角顶点放在点O 处．（1）如图1，若直角三角板DOE 的一边OD 放在射线OB 上，则∠COE =_______°；（2）如图2，将直角三角板DOE 绕点O 逆时针方向转动到某个位置，若OC 恰好平分∠BOE ，求∠BOD 、∠COE 的度数；（3）如图3，将直角三角板DOE 绕点O 转动，如果OD 始终在∠BOC 的内部，试猜想∠BOD 和∠COE 有怎样的数量关系？并说明理由．在一次数学活动课上，李磊同学将一副宜角三角板ABC 、ADE 按如图1放置，点A 、C 、D 在同一直线上，（30EAD Ð=°、45BAC Ð=°），并将三角板ABC 绕点A 顺时针旋转一定角度，且始终保持030CAD °<У°．（1）在旋转过程中，如图2，当点A 、C 、E 在同一直线上时，则BAD Ð=____；（2）在旋转过程中，如图3，当30BAE Ð=°时．请说明AC 平分DAE Ð；（3）在旋转过程中，如图4，当4BAE CAD Ð=Ð时，求此时CAE Ð的度数．如图1，一块三角板的一条直角边OC 放在直线AB 上．将图1中的三角板绕点O 顺时针旋转，使它的两直角边OC 、OD 均在直线AB 的上方，得图2；将图1中的三角板绕点O 逆时针旋转，使它的直角边OC 在直线AB 下方，OD 在直线AB 的上方得图3．OE 始终平分AOD Ð．（1）图1中，COE Ð的度数为______，BOD Ð=______；图2中，若35COE Ð=°，则BOD Ð=______．（2）在图2中，猜想BOD Ð与COE Ð数量关系，并说明理由．（3）在图3中，直接写出BOD Ð与COE Ð的数量关系．不必说明理由．如图，若:1:2BOC AOC ÐÐ=，66AOB Ð=°，且OC 在∠AOB 的内部，则AOC Ð=（）考点五 角n等分线的计算A ．22°B ．42°C ．72°D ．44°如图，AOC BOD Ð=Ð，30BOC Ð=°，12DOE AOD Ð=Ð，则AOE Ð=（ ）A ．10°B ．15°C ．20°D ．25°如图，已知:1:4AOC BOC ÐÐ=，OD 平分AOB Ð，且33COD Ð=°．请求出AOB Ð的度数．如图，AOC Ð与BOC Ð的度数比为5:2，OD 平分AOB Ð，若15COD Ð=°，求AOB Ð的度数．如图所示，平分，，，求的度数．OD AOC Ð322AOB Ð=Ð512BOC Ð=Ð2Ð已知130AOD Ð=°，50BOC Ð=°，OM 平分AOC Ð，ON 平分BOD Ð．（1）如图1，若:2:3AOM DON ÐÐ=，求NOC Ð的度数；（2）将BOC Ð顺时针旋转至图2的位置，求MON Ð的度数．如图，直线、相交于点，平分，平分，且，求的度数．如图，点A 、C 、B 三点在一直线上，从点C 引射线CD 、CE 、CF ，∠DCE =13∠ECA ，∠FCE =13∠ECB．AB CD O OE BOD ÐOF COE Ð1:21:4ÐÐ=AOFÐ（1）求∠DCF 的大小，并说明理由；（2）当∠DCE =1n ∠ECA ，∠FCE =1n∠ECB 时，直接写出∠DCF 的大小（用含n 的代数式表示）．点O 在直线AD 上，在直线AD 的同侧作射线OB ，OC ．（1）如图1，若40AOB Ð=°，:4:3BOC COD ÐÐ=，求BOC Ð的度数；（2）如图2，若OM 平分AOC Ð，ON 平分BOD Ð，130MON Ð=°，求BOC Ð的度数．阅读并解答：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角考点六求角度综合的角平分线，如图，OM 是AOC Ð的平分线，ON 是BOC Ð的平分线，（1）如图1，当AOB Ð是直角，60BOC Ð=°时，MON Ð的度数是多少？（2）如图2，当AOB a Ð=，60BOC Ð=°时，猜想MON Ð与a 的数量关系；（3）如图3，当AOB a Ð=，BOC b Ð=时，猜想MON Ð与a 、b 有数量关系吗？如果有，指出结论并说明理由．如图，以AOB Ð的顶点O 为端点画一条射线OC ，OM ON 、分别是AOC Ð和BOC Ð的角平分线．（1）如图①，若50,30AOC BOC Ð=°Ð=°，则MON Ð的度数是_________；（2）如图②，若100,30а°=Ð=AOB BOC ，则MON Ð的度数是_________．（3）根据以上解答过程，完成下列探究：①探究一：如图③，当射线OC 位于AOB Ð内部时，请写出AOB Ð与MON Ð的数量关系：__________．②探究二：如图④，当射线OC 位于AOB Ð外部时，请写出AOB Ð与MON Ð的数量关系，并说明理由．如图，OM 是AOC Ð的平分线，ON 是BOC Ð的平分线．（1）如图①，当AOB Ð是直角，60BOC Ð=°时，则MON Ð=___________（2）如图②，当AOB a Ð=，60BOC Ð=°时，猜想MON Ð与a 的数量关系，并说明理由．（3）如图③，当AOB a Ð=，BOC b Ð=时，猜想：MON Ð与a 、b 有数量关系吗？如果有，指出结论并说明理由．已知O 为直线AD 上一点，以O 为顶点作90COE Ð=°，射线OF 平分AOE Ð．（1）如图1，AOC Ð与DOE Ð的数量关系为_________，COF Ð和DOE Ð之间的数量关系为_________．（2）若将COE Ð绕点O 旋转至图2位置，射线OF 仍然平分AOE Ð，请写出COF Ð和DOE Ð这间的数量关系，并说明理由；（3）若将COE Ð绕点O 旋转至图3的位置，射线OF 仍然平分AOE Ð，请写出COF Ð和DOE Ð之间的数量关系，并说明理由．如图，是内部的一条射线，是内部的一条射线，是内部的一OB AOC ÐOM AOB ÐON BOCÐ条射线．（1）如图1，、分别是、的角平分线，已知，，求的度数；（2）如图2，若，，且，求的度数．如图1，射线、分别是，的平分线，．，三点，，在一直线上将从现在位置开始绕点逆时针每秒旋转，当与重合时，立即再将绕点顺时针每秒旋转，当与重合时，旋转停止．（1）若，求；（2）求的度数；（3）当旋转时，的大小不变，设边对应射线，边对应射线，旋转时间为秒，直接写出为何值时，对于（1）中，使成立．已知O 为直线AB 上一点，射线OD 、OC 、OE 位于直线AB 上方，OD 在OE的左侧，OM ON AOB ÐBOC Ð30AOB Ð=°70MON Ð=°BOC Ð140AOC Ð=°14AOM NOC AOB Ð=Ð=Ð:3:2BOM BON ÐÐ=MON ÐOB OE AOC ÐDOF Ð3AOD COD Ð=Ð2COE BOD Ð=ÐA O F COD ÐO 5°OC OA COD ÐO 5°OD OE AOC n COD Ð=Ðn COD ÐCOD ÐCOD ÐOC OC ¢OD OD ¢(0)t t >t n AOC n COD ¢¢Ð=Ð∠AOC =120°，∠DOE =80°．（1）如图1，当OD 平分∠AOC 时，求∠EOB 的度数；（2）点F 在射线OB 上，若射线OF 绕点O 逆时针旋转n °（0<n <180且n ≠60），∠FOA =3∠AOD ．当∠DOE 在∠AOC 内部（图2）和∠DOE 的两边在射线OC 的两侧（图3）时，∠FOE 和∠EOC 的数量关系是否改变，若改变，说明理由，若不变，求出其关系．已知 120=ÐAOB ，OC 、OD 是过点O 的射线，射线OM 、ON 分别平分∠AOC 和∠DOB ．（1）如图①，若OC 、OD 是∠AOB 的三等分线，则MON Ð=______°（2）如图②，若40COD Ð=°，AOC DOB йÐ，则MON Ð=______°（3）如图③，在∠AOB 内，若()060COD a a Ð=°<<°，则MON Ð=______°（4）将（3）中的∠COD 绕着点O 逆时针旋转到∠AOB 的外部（0180AOC <Ð<°，0180BOD <Ð<°），求此时∠MON 的度数．1.若130.45°Ð=，23028°¢Ð=，则1Ð_____2Ð（用“>”“=”“<”填空）．课后强化2.若∠A =20°19´，∠B =20°15´30＂，∠C =20.25°，则（ ）A ．∠A >∠B >∠C B ．∠B >∠A >∠C C ．∠A >∠C >∠BD ．∠C >∠A >∠B3.如图，在∠AOB 的内部取一点C ，在∠AOB 的外部取一点D ，作射线OC ，OD ．下列结论错误的是（）A ．∠AOB<∠AODB ．∠BOC<∠AOBC ．∠COD>∠AOD D ．∠AOB>∠AOC4.如图所示的网格是正方形网格，点A ，B ，C ，D ，O 是网格线交点，那么∠AOB ∠COD ．（填“>”，“<”或“=”）5.如图所示，其中最大的角是 ，∠DOC ，∠DOB ，∠DOA 的大小关系是 ．6.若47A Ð=°，则A Ð的余角的度数为（ ）A ．B ．C ．D ．7.互为补角的两个角的比是3:2，则较小角的余角等于（ ）A ．B ．C ．D ．8.若一个角的补角加上20°后等于这个角余角的3倍，则这个角的度数为（ ）A ．B ．C ．D ．9.一个角的补角与这个角的余角的和比平角少10°，则这个角的度数是 ．10.a Ð是b Ð的3倍，且b Ð的补角比a Ð的余角大110°，求a Ð的度数．12.一个角的余角比它的补角的23还少40°，则这个角为 度．13.如图，已知∠AOB =40°，∠BOC =3∠AOB ，OD 平分∠AOC ，求∠COD的度数．133°123°43°33°18°54°108°144°25°35°45°55°解：因为∠BOC =3∠AOB ，∠AOB =40°，所以∠BOC =°．所以∠AOC = + = °+ °= °．因为OD 平分∠AOC ，所以∠COD =12 =12× °= °．14.如图，已知∠AOB =90°，∠EOF =60°，OE 平分∠AOB ，OF 平分∠BOC ，求∠AOC 和∠COB 的度数．15.如图所示，OB 是∠AOC 的平分线，OD 是∠COE 的平分线．（1）如果∠AOB =50°，∠DOE =35°，那么∠BOD 是多少度？（2）如果∠AOE =160°，∠COD =25°，那么∠AOB 是多少度？16.如图，AOB Ð是平角，,OP OQ 分别是,AOC COD ÐÐ的角平分线．（1）若70,25BOD AOP Ð=°Ð=°，求DOQ Ð的度数；（2）若,AOD QOD a b Ð=Ð=，用含a 和b 的式子表示出AOP Ð的度数．17.一副三角板摆放在一起的示意图如下，若155Ð=°，则∠2的度数是______．18.如图，将一个三角板60°角的顶点与另一个三角板的直角顶点重合，若∠1=25°40′，则∠2=______．19.将一副三角板中的两块直角三角尺的直角顶点C 按如图方式叠放在一起．（1）若∠DCE=35°，则∠ACB的度数为______；（2）若∠ACB=144°42′，则∠DCE的度数为______；（3）猜想∠ACB与∠DCE的大小关系，并说明理由．20.如图，将两个直角三角板的顶点叠放在一起进行探究．（1）如图①，将一副直角三角板的直角顶点C叠放在一起，若CE恰好是∠ACB的平分线，请你猜想此时CB是不是∠ECD的平分线，并简述理由；（2）如图②，将一副直角三角板的直角顶点C叠放在一起，若CB始终在∠DCE的内部，请猜想∠ACE 与∠DCB是否相等，并简述理由；（3）如图③，若将两个同样的三角板中60°锐角的顶点A叠放在一起，请你猜想∠DAB与∠CAE有何关系，并说明理由．21.如图，已知，平分，且．请求出的度数．Ð=°AOBCODÐAOC BOC:1:4ÐÐ=OD AOBÐ3322.如图，与的度数比为，平分，若，求的度数．23.如图，2814AOB Ð=°¢，4BOC AOB Ð=Ð，OM 平分AOC Ð，求BOM Ð的度数．24.如图，在∠AOB 的内部有3条射线OC 、OD 、OE ，若∠AOC =70°，∠BOE =1n ∠BOC ，∠BOD =1n∠AOB ，则∠DOE =_______°．（用含n 的代数式表示）25.如图1，OC 是∠AOB 的平分线，且13BOD COD Ð=Ð．AOC ÐBOC Ð5:2OD AOB Ð15COD Ð=°AOBÐ（1）当15BOD Ð=°时，求∠AOB 的度数：（2）如图2，若射线OP 在AOD Ð的内部，且POD AOB Ð=Ð，请直接写出图中相等的四对角．（POD AOB Ð=Ð和BOC AOC Ð=Ð除外）26.已知COD Ð在AOB Ð的内部，且150AOB Ð=°，15COD AOB Ð=Ð，射线OE 平分AOD Ð．（1）若70AOC Ð=°，求AOE Ð的度数；（2）若24COE Ð=°，求BOC Ð的度数．27.如图，OB 是AOC Ð的平分线，OD 是COE Ð的平分线．（1）如果70AOC Ð=°，50COE Ð=°，求BOD Ð的度数；（2）如果160AOE Ð=°，求BOD Ð的度数；（3）如果OM平分AOEÐ=°，求BODÐ的度数．COMÐÐ=，15Ð，:2:3COD BOC28.如图1，在∠AOB中，OC是∠AOB内部任意一条射线，ON、OM分别平分∠AOC和∠BOC．（1）若∠AOB=100°，求∠MON的度数．（2）若∠AOB=ɑ，直接写出∠MON的度数= （结果用含α的代数式表示）．（3）若射线OC在∠AOB外部（∠BOC<180°），其它条件不变，如图2所示，∠AOB=a，求∠MON的度数（结果用含a的代数式表示）．29.多多对几何中角平分线等兴趣浓厚，请你和多多一起探究下面问题吧．已知∠AOB=100°，射线OE，OF 分别是∠AOC和∠COB的角平分线．（1）如图1，若射线OC在∠AOB的内部，且∠AOC=30°，求∠EOF的度数；（2）如图2，若射线OC在∠AOB的内部绕点O旋转，则∠EOF的度数_____；（3）若射线OC在∠AOB的外部绕点O旋转（旋转中∠AOC，∠BOC均指小于180°的角），其余条件不变，请借助图3探究∠EOF的大小，请直接写出∠EOF的度数（不写探究过程）．。

中点及角平分线（讲义）知识点睛1.线段上的点把线段分成相等的两条线段，则这个点叫做线段的．2.如图，若点C 为线段AB 的中点，则中点的六种表示是．A C B3.从一个角的顶点引出一条，把这个角分成两个相等的角，这条叫做这个角的平分线．4.如图，若OC 为∠AOB 的平分线，则角平分线的六种表示是．ACO B 精讲精练1.已知：如图，线段AB=10 cm，点C 是线段AB 的中点，求AC 的长．A C B2.已知：如图，点C 是线段AB 的中点，AC=4 cm，求AB 的长．C B3.已知：如图，线段AB=10 cm，AD=6 cm，点C 是线段AD 的中点，求BC的长．A C D B4.如图，线段AB=4，点O 是线段AB 上一点，点C，D 分别是线段OA，OB 的中点，求CD 的长．A C O D B5.已知：如图，∠AOB=70°，OC 平分∠AOB，求∠AOC 的度数．ACO A N6. 如图，已知 OC 平分∠AOB ，OD 平分∠AOC ，且∠COD =25°， 求∠AOB 的度数．A DCO B7. 如图，∠AOB =90°，∠AOC =50°，OM 平分∠BOC ，ON 平分∠AOC ，求∠MON 的度数．BMC8.如图，点O 为直线AB 上一点，∠AOC=50°，OD 平分∠AOC，∠DOE=90°．（1）求∠BOD 的度数；（2）通过计算说明OE 是否平分∠BOC．C EDA O B【参考答案】知识点睛1.中点2.AC=BC，BC=ACAC 1AB ，BC1AB 2 2AB=2AC，AB=2BC3.射线，射线4.∠AOC=∠BOC，∠BOC=∠AOC，∠AOC= 1∠AOB，∠BOC=1∠AOB 2 2∠AOB=2∠AOC，∠AOB=2∠BOC精讲精练1. 5 cm2.8 cm3.7 cm4. 25. 35°6. 100°7. 45°8. （1）155°；（2）平分，理由略。