正切余切

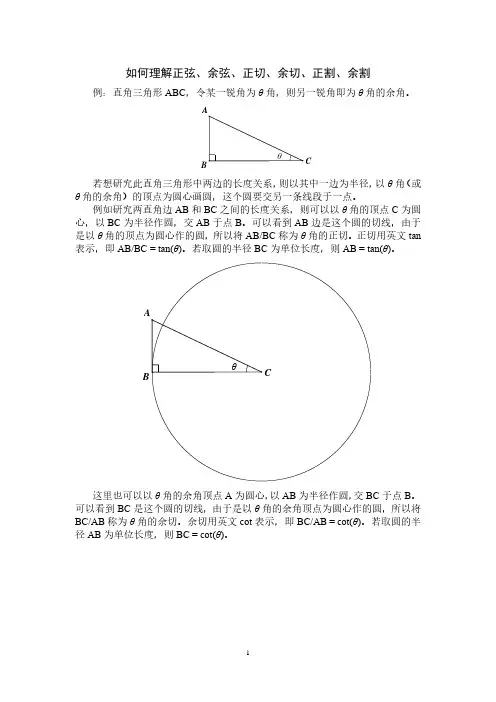
如何理解正弦、余弦、正切、余切、正割、余割例：直角三角形ABC ，令某一锐角为θ角，则另一锐角即为θ角的余角。

若想研究此直角三角形中两边的长度关系，则以其中一边为半径，以θ角（或θ角的余角）的顶点为圆心画圆，这个圆要交另一条线段于一点。

例如研究两直角边AB 和BC 之间的长度关系，则可以以θ角的顶点C 为圆心，以BC 为半径作圆，交AB 于点B 。

可以看到AB 边是这个圆的切线，由于是以θ角的顶点为圆心作的圆，所以将AB/BC 称为θ角的正切。

正切用英文tan 表示，即AB/BC = tan(θ)。

若取圆的半径BC 为单位长度，则AB = tan(θ)。

这里也可以以θ角的余角顶点A 为圆心，以AB 为半径作圆，交BC 于点B 。

可以看到BC 是这个圆的切线，由于是以θ角的余角顶点为圆心作的圆，所以将BC/AB 称为θ角的余切。

余切用英文cot 表示，即BC/AB = cot(θ)。

若取圆的半径AB 为单位长度，则BC = cot(θ)。

C研究θ角的两边AC 和BC 之间的长度关系。

则可以以θ角的顶点C 为圆心，以BC 为半径作圆，交AC 于点D 。

可以看到AC 边是这个圆的割线，由于是以θ角的顶点为圆心作的圆，所以将AC/BC 称为θ角的正割。

正割用英文sec 表示，即AC/BC = sec(θ)。

若取圆的半径BC 为单位长度，则AC = sec(θ)。

这里也可以以θ角的余角顶点A 为圆心，以AC 为半径作圆，交BC 于点C 。

若将BC 延长，则可以看到BC 边是这个圆的半弦。

由于是以θ角的余角顶点为圆心作的圆，所以将BC/AC 称为θ角的余弦。

余弦用英文cos 表示，即BC/AC = cos(θ)。

若取圆的半径AC 为单位长度，则BC = cos(θ)。

C研究θ角的余角的两边AB和AC之间的长度关系，则可以以θ角的顶点C 为圆心，以AC为半径作圆，交AB于点A。

若将AB延长，则可以看到AB边是这个圆的半弦。

余弦正弦正切大小关系正弦余弦正切的关系：sinA/cosA=tanA，三角函数是基本初等函数之一，是以角度为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

也可以等价地用与单位圆有关的各种线段的长度来定义。

三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。

在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。

正弦；在直角三角形中，任意一锐角∠a的对边与斜边的比叫做角a的正弦；余弦：在直角三角形中，任意一锐角∠a的邻边与斜边的比叫做角a的余弦；正切：在直角三角形中，任意一锐角∠a的对边与邻边的比叫做角a的正切；余切：在直角三角形中，任意一锐角∠a的邻边与对边的比叫做角a的余切。

关系：在直角三角形中，任意一个锐角的正弦值等于另一个锐角的余弦值；任意一个角的正弦值与余弦值的积为一。

正弦余弦正切余切九大关系公式：三角函数公式：正弦（sin）：角α的对边比上斜边。

余弦（cos）：角α的邻边比上斜边。

正切（tan）：角α的对边比上邻边。

余切（cot）：角α的邻边比上对边。

正割（sec）：角α的斜边比上邻边。

余割（csc）：角α的斜边比上对边。

同角三角函数：平方关系：sin^2(α）＋cos^2(α）＝1。

tan^2(α）＋1=sec^2(α）。

cot^2(α）＋1=csc^2(α）。

积的关系：sinα＝tanαcosαcosα＝cotαsinα。

tanα＝sinαsecαcotα＝cosαcscα。

secα＝tanαcscαcscα＝secαcotα。

三角函数的倒数与余切与余割与正割与余弦与正弦公式三角函数是数学中常见的一类函数，包括正弦、余弦、正切、余切、正割、余割六种。

在三角函数中，倒数与余切与余割与正割与余弦与正弦之间存在一些特定的公式和关系。

本文将探讨这些公式和关系，并介绍它们的应用。

一、倒数与余切公式倒数是指一个数的倒数，记作x的倒数为1/x。

在三角函数中，正切的倒数称为余切，表示为cot(x)。

余切的定义为余切(x) = 1/tan(x)。

余切(x)有以下公式：cot(x) = cos(x)/sin(x)cot(x) = 1/tan(x)倒数与余切公式的应用非常广泛。

它们在解三角方程、计算三角函数值和求解实际问题中经常被使用。

二、余割与正割公式余割和正割是三角函数中与正弦和余弦有关的函数。

余割的定义为csc(x) = 1/sin(x)。

余割(x)有以下公式：csc(x) = 1/sin(x)csc(x) = 1/cos(x)/tan(x) = cos(x)/sin(x)正割的定义为sec(x) = 1/cos(x)。

正割(x)有以下公式：sec(x) = 1/cos(x)sec(x) = 1/sin(x)/cot(x) = 1/cos(x)/sin(x)余割与正割公式的应用也非常广泛。

它们在解三角方程、计算三角函数值和求解实际问题中经常被使用。

三、余弦与正弦公式余弦和正弦是三角函数中最为常见的两种函数。

余弦与正弦有以下公式：cos(x) = 1/sin(x)/tan(x)cos(x) = sqrt(1 - sin^2(x))（平方根）cos^2(x) + sin^2(x) = 1正弦与余弦公式在解三角方程、计算三角函数值和求解实际问题中都有重要的应用。

综上所述，三角函数的倒数与余切与余割与正割与余弦与正弦公式在数学和实际应用中起着重要的作用。

这些公式可以帮助我们解决各种三角函数相关的问题，提高计算的准确性和效率。

因此，在学习和应用三角函数时，我们应该充分理解和掌握这些公式的意义和用法。

三角函数的正切与余切的关系三角函数是数学中一个重要的分支，其中正切和余切是两个常见的三角函数。

正切函数和余切函数之间存在着一定的关系，本文将探讨正切与余切之间的关系以及相关性质。

一、正切和余切的定义1. 正切函数的定义正切函数（tangent function）是指在单位圆上，某一角的正切值等于这个角的对边长度与邻边长度的比值。

设角度为θ，那么正切函数的定义公式可以表示为：tan(θ) = sin(θ) / cos(θ)2. 余切函数的定义余切函数（cotangent function）是指在单位圆上，某一角的余切值等于这个角的邻边长度与对边长度的比值。

设角度为θ，那么余切函数的定义公式可以表示为：cot(θ) = cos(θ) / sin(θ)二、正切与余切的关系1. 互为倒数关系正切函数与余切函数之间存在互为倒数的关系。

可以通过以上定义公式进行证明：tan(θ) = sin(θ) / cos(θ)cot(θ) = cos(θ) / sin(θ)将正切函数的定义公式中的sin(θ) / cos(θ) 乘上cos(θ) / cos(θ)，得到：tan(θ) = sin(θ) / cos(θ) * cos(θ) / cos(θ)= sin(θ) * cos(θ) / (cos^2(θ))根据三角恒等式sin^2(θ) + cos^2(θ) = 1，我们可以将cos^2(θ) 转换成 1 - sin^2(θ)，代入上式：tan(θ) = sin(θ) * (1 - sin^2(θ)) / (1 - sin^2(θ))= sin(θ) * (1 - sin^2(θ)) / cos^2(θ)根据三角恒等式sin^2(θ)+ cos^2(θ) = 1，可以将上式简化为：tan(θ) = sin(θ) / cos^2(θ)= 1 / (cos(θ) / sin(θ))= 1 / cot(θ)所以，正切函数与余切函数之间满足互为倒数的关系。

《正切和余切》数学教案第一章：正切和余切的定义与性质1.1 教学目标了解正切和余切的定义掌握正切和余切的基本性质能够运用正切和余切解决简单问题1.2 教学内容引出正切和余切的定义讲解正切和余切的性质举例说明正切和余切的运用1.3 教学方法采用讲授法讲解正切和余切的定义和性质通过例题演示正切和余切的运用引导学生进行分组讨论和练习1.4 教学评估课堂问答：检查学生对正切和余切的定义和性质的理解练习题：让学生运用正切和余切解决实际问题第二章：正切和余切的图像与性质2.1 教学目标了解正切和余切的图像特点掌握正切和余切的基本性质能够运用正切和余切图像解决简单问题2.2 教学内容讲解正切和余切的图像特点分析正切和余切的性质与图像的关系举例说明正切和余切图像的运用2.3 教学方法采用讲授法讲解正切和余切的图像特点通过例题演示正切和余切图像的运用引导学生进行分组讨论和练习2.4 教学评估课堂问答：检查学生对正切和余切图像特点的理解练习题：让学生运用正切和余切图像解决实际问题第三章：正切和余切的三角函数值3.1 教学目标掌握正切和余切的三角函数值能够运用正切和余切的三角函数值解决简单问题理解正切和余切三角函数值的应用范围3.2 教学内容讲解正切和余切的三角函数值分析正切和余切三角函数值的运用举例说明正切和余切三角函数值的运用3.3 教学方法采用讲授法讲解正切和余切的三角函数值通过例题演示正切和余切三角函数值的运用引导学生进行分组讨论和练习3.4 教学评估课堂问答：检查学生对正切和余切的三角函数值的理解练习题：让学生运用正切和余切的三角函数值解决实际问题第四章：正切和余切的三角函数公式4.1 教学目标掌握正切和余切的三角函数公式能够运用正切和余切的三角函数公式解决简单问题理解正切和余切三角函数公式的应用范围4.2 教学内容讲解正切和余切的三角函数公式分析正切和余切三角函数公式的运用举例说明正切和余切三角函数公式的运用4.3 教学方法采用讲授法讲解正切和余切的三角函数公式通过例题演示正切和余切三角函数公式的运用引导学生进行分组讨论和练习4.4 教学评估课堂问答：检查学生对正切和余切的三角函数公式的理解练习题：让学生运用正切和余切的三角函数公式解决实际问题第五章：正切和余切的三角函数应用5.1 教学目标掌握正切和余切的三角函数应用能够运用正切和余切的三角函数解决实际问题理解正切和余切三角函数应用的实际意义5.2 教学内容讲解正切和余切的三角函数应用分析正切和余切三角函数应用的实例举例说明正切和余切三角函数应用的实际问题5.3 教学方法采用讲授法讲解正切和余切的三角函数应用通过例题演示正切和余切三角函数应用的实际问题引导学生进行分组讨论和练习5.4 教学评估课堂问答：检查学生对正切和余切的三角函数应用的理解练习题：让学生运用正切和余切的三角函数解决实际问题第六章：正切和余切的三角函数化简6.1 教学目标掌握正切和余切的三角函数化简方法能够运用正切和余切的三角函数化简实际问题理解正切和余切三角函数化简的实际意义6.2 教学内容讲解正切和余切的三角函数化简方法分析正切和余切的三角函数化简实例举例说明正切和余切的三角函数化简的实际问题6.3 教学方法采用讲授法讲解正切和余切的三角函数化简方法通过例题演示正切和余切的三角函数化简的实际问题引导学生进行分组讨论和练习6.4 教学评估课堂问答：检查学生对正切和余切的三角函数化简的理解练习题：让学生运用正切和余切的三角函数化简解决实际问题第七章：正切和余切的三角函数变换7.1 教学目标掌握正切和余切的三角函数变换方法能够运用正切和余切的三角函数变换解决实际问题理解正切和余切三角函数变换的实际意义7.2 教学内容讲解正切和余切的三角函数变换方法分析正切和余切的三角函数变换实例举例说明正切和余切的三角函数变换的实际问题7.3 教学方法采用讲授法讲解正切和余切的三角函数变换方法通过例题演示正切和余切的三角函数变换的实际问题引导学生进行分组讨论和练习7.4 教学评估课堂问答：检查学生对正切和余切的三角函数变换的理解练习题：让学生运用正切和余切的三角函数变换解决实际问题第八章：正切和余切的三角函数在几何中的应用8.1 教学目标掌握正切和余切的三角函数在几何中的应用方法能够运用正切和余切的三角函数解决几何问题理解正切和余切三角函数在几何中的实际意义8.2 教学内容讲解正切和余切的三角函数在几何中的应用方法分析正切和余切的三角函数在几何中的应用实例举例说明正切和余切的三角函数在几何中的实际问题8.3 教学方法采用讲授法讲解正切和余切的三角函数在几何中的应用方法通过例题演示正切和余切的三角函数在几何中的应用实例引导学生进行分组讨论和练习8.4 教学评估课堂问答：检查学生对正切和余切的三角函数在几何中的理解练习题：让学生运用正切和余切的三角函数解决几何问题第九章：正切和余切的三角函数在物理中的应用9.1 教学目标掌握正切和余切的三角函数在物理中的应用方法能够运用正切和余切的三角函数解决物理问题理解正切和余切三角函数在物理中的实际意义9.2 教学内容讲解正切和余切的三角函数在物理中的应用方法分析正切和余切的三角函数在物理中的应用实例举例说明正切和余切的三角函数在物理中的实际问题9.3 教学方法采用讲授法讲解正切和余切的三角函数在物理中的应用方法通过例题演示正切和余切的三角函数在物理中的应用实例引导学生进行分组讨论和练习9.4 教学评估课堂问答：检查学生对正切和余切的三角函数在物理中的理解练习题：让学生运用正切和余切的三角函数解决物理问题第十章：正切和余切的三角函数在工程中的应用10.1 教学目标掌握正切和余切的三角函数在工程中的应用方法能够运用正切和余切的三角函数解决工程问题理解正切和余切三角函数在工程中的实际意义10.2 教学内容讲解正切和余切的三角函数在工程中的应用方法分析正切和余切的三角函数在工程中的应用实例举例说明正切和余切的三角函数在工程中的实际问题10.3 教学方法采用讲授法讲解正切和余切的三角函数在工程中的应用方法通过例题演示正切和重点和难点解析一、正切和余切的定义与性质1. 环节重点：理解正切和余切的定义，掌握它们的基本性质。

函数名正弦余弦正切余切正割余割符号 sin cos tan cot sec csc正弦函数 sin（A）=a/h余弦函数 cos（A）=b/h正切函数 tan（A）=a/b余切函数 cot（A）=b/a在某一变化过程中，两个变量x、y，对于某一范围内的x的每一个值，y都有确定的值和它对应，y就是x的函数。

这种关系一般用y=f(x)来表示。

两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosA ?cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA) ?cot(A-B)=(cotAcotB+1)/(cotB-cotA)倍角公式tan2A=2tanA/[1-(tanA)^2]cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^2sin2A=2sinA*cosA三倍角公式sin3a=3sina-4(sina)^3cos3a=4(cosa)^3-3cosatan3a=tana*tan(π/3+a)*tan(π/3-a)半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA)) ? tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA)和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B) )2cosAcosB=cos(A+B)+cos(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB积化和差公式sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(pi/2-a)=cos(a)cos(pi/2-a)=sin(a)sin(pi/2+a)=cos(a)cos(pi/2+a)=-sin(a)sin(pi-a)=sin(a)cos(pi-a)=-cos(a)sin(pi+a)=-sin(a)cos(pi+a)=-cos(a)tgA=tanA=sinA/cosA万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中，tan(c)=b/a] a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中，tan(c)=a/b] 1+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2其他非重点三角函数csc(a)=1/sin(a)sec(a)=1/cos(a)双曲函数sinh(a)=(e^a-e^(-a))/2cosh(a)=(e^a+e^(-a))/2tgh(a)=sinh(a)/cosh(a)。

余切,正割,余割函数求导在微积分学中，我们经常会遇到三角函数的求导问题。

三角函数包括：正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。

其中，正割函数和余割函数的求导相对来说比较容易，但是，余切函数的求导可能会让人感到困惑。

在本文中，我们将详细介绍余切、正割和余割函数的求导方法。

一、余切函数求导先来看一下余切函数的定义：$\cot{a}=\frac{1}{\tan{a}}=\frac{\cos{a}}{\sin{a}}$。

我们可以用导数的定义来求余切函数的导数：$$\frac{d}{dx}\cot{x} = \lim_{h \to 0} \frac{\cot{(x+h)} -\cot{x}}{h}$$将 $\cot{(x+h)}$ 和 $\cot{x}$ 的值带入，并将分式进行化简得：$$\frac{d}{dx}\cot{x} = \lim_{h \to 0}\frac{\frac{\cos{(x+h)}}{\sin{(x+h)}} -\frac{\cos{x}}{\sin{x}}}{h} \\= \lim_{h \to 0} \frac{\cos{(x+h)}\sin{x} -\cos{x}\sin{(x+h)}}{h\sin{(x+h)}\sin{x}} \\= \lim_{h \to 0} \frac{\cos{(x+h)}\sin{x} -\cos{x}\sin{(x+h)}}{h\sin{x}\cos{h} + h\cos{x}\sin{h}} \\= \lim_{h \to 0} \frac{\cos{(x+h)}\sin{x} -\cos{x}\sin{(x+h)}}{h(\sin{x}\cos{h} + \cos{x}\sin{h})} \\ = \lim_{h \to 0} \frac{\cos{x}\sin{h} -\sin{x}\cos{h}}{h(\sin{x}\cos{h} + \cos{x}\sin{h})} \\= -\frac{1}{\sin^2{x}}$$因此，余切函数的导数为 $-\frac{1}{\sin^2{x}}$。

《正切和余切》数学教案第一章：正切和余切的定义1.1 引入正切和余切的定义通过生活中的实际例子，让学生感受正切和余切的概念利用直角三角形，引导学生理解正切和余切的定义1.2 学习正切和余切的功能和性质通过图形和实例，让学生了解正切和余切的功能和性质引导学生探索正切和余切的单调性、周期性等特性1.3 练习正切和余切的计算提供一些简单的正切和余切计算题目，让学生进行练习引导学生总结正切和余切的计算方法和解题技巧第二章：正切和余切的图像2.1 学习正切和余切的图像通过图形和实例，让学生了解正切和余切的图像特点引导学生探索正切和余切图像的周期性、奇偶性等特性2.2 分析正切和余切的图像提供一些正切和余切的图像题目，让学生进行分析和解答引导学生运用正切和余切的图像解决实际问题第三章：正切和余切的应用3.1 学习正切和余切的应用通过实例，让学生了解正切和余切在实际问题中的应用引导学生运用正切和余切解决几何、物理等问题3.2 练习正切和余切的应用题目提供一些正切和余切的应用题目，让学生进行练习引导学生总结正切和余切在实际问题中的应用方法和技巧第四章：正切和余切的综合练习4.1 综合练习正切和余切的知识提供一些综合性的正切和余切题目，让学生进行练习引导学生运用正切和余切的知识解决综合问题4.2 分析正切和余切的综合题目提供一些正切和余切的综合题目，让学生进行分析和解答引导学生运用正切和余切的知识解决实际问题第五章：正切和余切的巩固与提高5.1 巩固正切和余切的知识提供一些巩固性的正切和余切题目，让学生进行练习引导学生总结正切和余切的知识点和解题技巧5.2 提高正切和余切的能力提供一些提高性的正切和余切题目，让学生进行练习引导学生运用正切和余切的知识解决复杂问题第六章：正切和余切的三角函数6.1 引入正切和余切的三角函数通过生活中的实际例子，让学生感受正切和余切的三角函数的概念利用直角三角形，引导学生理解正切和余切的三角函数的定义6.2 学习正切和余切的三角函数的功能和性质通过图形和实例，让学生了解正切和余切的三角函数的功能和性质引导学生探索正切和余切的三角函数的单调性、周期性等特性6.3 练习正切和余切的三角函数的计算提供一些简单的正切和余切的三角函数计算题目，让学生进行练习引导学生总结正切和余切的三角函数的计算方法和解题技巧第七章：正切和余切的三角函数图像7.1 学习正切和余切的三角函数图像通过图形和实例，让学生了解正切和余切的三角函数的图像特点引导学生探索正切和余切的三角函数图像的周期性、奇偶性等特性7.2 分析正切和余切的三角函数图像提供一些正切和余切的三角函数图像题目，让学生进行分析和解答引导学生运用正切和余切的三角函数图像解决实际问题第八章：正切和余切的三角函数的应用8.1 学习正切和余切的三角函数的应用通过实例，让学生了解正切和余切的三角函数在实际问题中的应用引导学生运用正切和余切的三角函数解决几何、物理等问题8.2 练习正切和余切的三角函数的应用题目提供一些正切和余切的三角函数的应用题目，让学生进行练习引导学生总结正切和余切的三角函数在实际问题中的应用方法和技巧第九章：正切和余切的三角函数的综合练习9.1 综合练习正切和余切的三角函数的知识提供一些综合性的正切和余切的三角函数题目，让学生进行练习引导学生运用正切和余切的三角函数的知识解决综合问题9.2 分析正切和余切的三角函数的综合题目提供一些正切和余切的三角函数的综合题目，让学生进行分析和解答引导学生运用正切和余切的三角函数的知识解决实际问题第十章：正切和余切的三角函数的巩固与提高10.1 巩固正切和余切的三角函数的知识提供一些巩固性的正切和余切的三角函数题目，让学生进行练习引导学生总结正切和余切的三角函数的知识点和解题技巧10.2 提高正切和余切的三角函数的能力提供一些提高性的正切和余切的三角函数题目，让学生进行练习引导学生运用正切和余切的三角函数的知识解决复杂问题重点解析本《正切和余切》数学教案的重点和难点如下：重点：1. 正切和余切的定义及其性质2. 正切和余切的图像特点和周期性3. 正切和余切的应用方法和技巧4. 正切和余切的三角函数的概念和性质5. 正切和余切的三角函数的图像特点和周期性6. 正切和余切的三角函数的应用方法和技巧7. 正切和余切的三角函数的综合练习和解题技巧难点：1. 正切和余切的性质和图像的深入理解2. 正切和余切的三角函数的复杂计算和解题技巧3. 正切和余切的三角函数在实际问题中的应用方法和技巧4. 正切和余切的三角函数的综合题目分析和解答。

高考数学知识点：正切、余切函数的图象与性质_知识点总结
高考数学知识点：正切、余切函数的图象与性质正切函数的图像：余切函数的图像：
正切函数的性质：
（1）定义域：；
（2）值域是R，在上面定义域上无最大值也无最小值；
（3）周期性：是周期函数且周期是π，它与直线y=a的两个相邻交点之间的距离是一个周期π；
（4）奇偶性：是奇函数，对称中心是（k∈Z），无对称轴；
（5）单调性：正切函数在开区间内都是增函数。

但要注意在整个定义域上不具有单调性。

余切函数的性质:
（1）定义域：x
（2）值域：实数集R；
（3）周期性：是周期函数，周期为kπ（k∈Z且k≠0），最小正周期T=π
（4）奇偶性：奇函数，图像关于（，0）（k∈z）对称，实际上所有的零点都是它的对称中心（5）单调性：在每一个开区间（kπ,课前预习，（k+1）π），（k∈Z）上都是减函数，在整个定义域上不具有单调性。