二聚类与判别
- 格式:doc
- 大小:331.50 KB
- 文档页数:10

应用数理统计作业二学号:姓名:电话:二〇一四年十二月对NBA球队的聚类分析和判别分析摘要:NBA联盟作为篮球的最高殿堂深受广大球迷的喜爱,联盟的30支球队大家也耳熟能详,本文选取NBA联盟30支球队2013-2014常规赛赛季场均数据。
利用spss软件通过聚类分析对27个地区进行实力类型分类,并利用判断分析对其余3支球队对分类结果进行验证。
可以看出各球队实力类型与赛季实际结果相吻合。
关键词:聚类分析,判别分析,NBA目录1. 引言 (4)2、相关统计基础理论 (5)2.1、聚类分析 (5)2.2,判别分析 (6)3.聚类分析 (7)3.1数据文件 (7)3.2聚类分析过程 (9)3.3 聚类结果分析 (11)4、判别分析 (12)4.1 判别分析过程 (12)4.2判别检验 (17)5、结论 (20)参考文献 (21)致谢 (22)1. 引言1896年,美国第一个篮球组织"全国篮球联盟(简称NBL)"成立,但当时篮球规则还不完善,组织机构也不健全,经过几个赛季后,该组织就名存实亡了。
1946年4月6日,由美国波士顿花园老板沃尔特.阿.布朗发起成立了“美国篮球协会”(简称BAA)。
1949年在布朗的努力下,美国两大篮球组织BAA和NBL合并为“全国篮球协会”(简称NBA)。
NBA季前赛是 NBA各支队伍的热身赛,因为在每个赛季结束后,每支球队在阵容上都有相当大的变化,为了让各队磨合阵容,熟悉各自球队的打法,确定各队新赛季的比赛阵容、同时也能增进队员、教练员之间的沟通,所以在每个赛季开始之前,NBA就举办若干场季前赛,使他们能以比较好的状态投入到漫长的常规赛的比赛当中。
为了扩大NBA在全球的影响,季前赛有约三分之一的球队在美国以外的国家举办。
从总体上看,NBA的赛程安排分为常规赛、季后赛和总决赛。
常规赛采用主客场制,季后赛和总决赛采用七场四胜制的淘汰制。
[31]NBA常规赛从每年的11月的第一个星期二开罗,到次年的4月20日左右结束。



判别分析与聚类分析的基本原理数据分析是在如今信息时代中,越来越重要的一项技能。
在数据分析的过程中,判别分析和聚类分析是两个非常重要的方法。
本文将介绍判别分析和聚类分析的基本原理,以及它们在数据分析中的应用。
一、判别分析的基本原理判别分析是一种用于分类问题的统计方法,其目的是通过学习已知类别的样本数据,来构建一个分类器,从而对未知样本进行分类。
判别分析的基本原理可以简单概括为以下几个步骤:1. 数据预处理:首先需要对数据进行预处理,包括数据清洗、缺失值处理、特征选择等,以获得更好的数据质量。
2. 特征提取:在进行判别分析之前,需要将原始数据转化为有效的特征。
特征提取的方法有很多种,常用的包括主成分分析、线性判别分析等。
3. 训练分类器:利用判别分析算法对已知类别的样本数据进行训练,建立分类模型。
常用的判别分析方法有线性判别分析、二次判别分析等。
4. 分类预测:通过训练好的分类器,对未知样本进行分类预测。
分类预测的结果可以是离散的类标签,也可以是概率值。
判别分析广泛应用于医学、金融、市场营销等领域。
例如,在医学领域,可以利用判别分析来预测疾病的状态,辅助医生做出诊断决策。
二、聚类分析的基本原理聚类分析是一种无监督学习方法,其目的是将相似的数据对象分组,使得同一组内的对象相似度较高,不同组间的相似度较低。
聚类分析的基本原理可以概括为以下几个步骤:1. 选择相似性度量:首先需要选择一个合适的相似性度量,用于评估数据对象之间的相似程度。
常用的相似性度量包括欧氏距离、曼哈顿距离等。
2. 选择聚类算法:根据具体的问题需求,选择合适的聚类算法。
常用的聚类算法有K-means、层次聚类等。
3. 确定聚类数目:根据实际问题,确定聚类的数目。
有些情况下,聚类数目事先是已知的,有些情况下需要通过评价指标进行确定。
4. 根据聚类结果进行分析:将数据对象划分到各个聚类中,并对聚类结果进行可视化和解释。
聚类分析被广泛应用于市场分析、图像处理、社交网络等领域。



判别分析与聚类分析判别分析与聚类分析是数据分析领域中常用的两种分析方法。
它们都在大量数据的基础上通过统计方法进行数据分类和归纳,从而帮助分析师或决策者提取有用信息并作出相应决策。
一、判别分析:判别分析是一种有监督学习的方法,常用于分类问题。
它通过寻找最佳的分类边界,将不同类别的样本数据分开。
判别分析可以帮助我们理解和解释不同变量之间的关系,并利用这些关系进行预测和决策。
判别分析的基本原理是根据已知分类的数据样本,建立一个判别函数,用来判断未知样本属于哪个分类。
常见的判别分析方法包括线性判别分析(LDA)和二次判别分析(QDA)。
线性判别分析假设各类别样本的协方差矩阵相同,而二次判别分析则放宽了这个假设。
判别分析的应用广泛,比如在医学领域可以通过患者的各种特征数据(如生理指标、疾病症状等)来预测患者是否患有某种疾病;在金融领域可以用来判断客户是否会违约等。
二、聚类分析:聚类分析是一种无监督学习的方法,常用于对数据进行分类和归纳。
相对于判别分析,聚类分析不需要预先知道样本的分类,而是根据数据之间的相似性进行聚类。
聚类分析的基本思想是将具有相似特征的个体归为一类,不同类别之间的个体则具有明显的差异。
聚类分析可以帮助我们发现数据中的潜在结构,识别相似的群组,并进一步进行深入分析。
常见的聚类分析方法包括层次聚类分析(HCA)和k-means聚类分析等。
层次聚类分析基于样本间的相似性,通过逐步合并或分割样本来构建聚类树。
而k-means聚类分析则是通过设定k个初始聚类中心,迭代更新样本的分类,直至达到最优状态。
聚类分析在市场细分、社交网络分析、图像处理等领域具有广泛应用。
例如,可以将客户按照他们的消费喜好进行分组,以便为不同群体提供有针对性的营销活动。
总结:判别分析和聚类分析是两种常用的数据分析方法。
判别分析适用于已知分类的问题,通过建立判别函数对未知样本进行分类;聚类分析适用于未知分类的问题,通过数据的相似性进行样本聚类。


聚类分析聚类分析和判别分析有相似的作用,都是起到分类的作用。
但是,判别分析是已知分类然后总结出判别规则,是一种有指导的学习;而聚类分析则是有了一批样本,不知道它们的分类,甚至连分成几类也不知道,希望用某种方法把观测进行合理的分类,使得同一类的观测比较接近,不同类的观测相差较多,这是无指导的学习。
所以,聚类分析依赖于对观测间的接近程度(距离)或相似程度的理解,定义不同的距离量度和相似性量度就可以产生不同的聚类结果。
SAS/STAT中提供了谱系聚类、快速聚类、变量聚类等聚类过程。
谱系聚类方法介绍谱系聚类是一种逐次合并类的方法,最后得到一个聚类的二叉树聚类图。
其想法是,对于个观测,先计算其两两的距离得到一个距离矩阵,然后把离得最近的两个观测合并为一类,于是我们现在只剩了个类(每个单独的未合并的观测作为一个类)。
计算这个类两两之间的距离,找到离得最近的两个类将其合并,就只剩下了个类……直到剩下两个类,把它们合并为一个类为止。
当然,真的合并成一个类就失去了聚类的意义,所以上面的聚类过程应该在某个类水平数(即未合并的类数)停下来,最终的类就取这些未合并的类。
决定聚类个数是一个很复杂的问题。
设观测个数为,变量个数为,为在某一聚类水平上的类的个数,为第个观测,是当前(水平)的第类,为中的观测个数,为均值向量,为类中的均值向量(中心),为欧氏长度,为总离差平方和,为类的类内离差平方和,为聚类水平对应的各类的类内离差平方和的总和。
假设某一步聚类把类和类合并为下一水平的类,则定义为合并导致的类内离差平方和的增量。
用代表两个观测之间的距离或非相似性测度,为第水平的类和类之间的距离或非相似性测度。
进行谱系聚类时,类间距离可以直接计算,也可以从上一聚类水平的距离递推得到。
观测间的距离可以用欧氏距离或欧氏距离的平方,如果用其它距离或非相似性测度得到了一个观测间的距离矩阵也可以作为谱系聚类方法的输入。
根据类间距离的计算方法的不同,有多种不同的聚类方法。
聚类分析及判别分析案例⼀、案例背景随着现代⼈⼒资源管理理论的迅速发展,绩效考评技术⽔平也在不断提⾼。
绩效的多因性、多维性,要求对绩效实施多标准⼤样本科学有效的评价。
对企业来说,对上千⼈进⾏多达50~60个标准的考核是很常见的现象。
但是,⽬前多标准⼤样本⼤型企业绩效考评问题仍然困扰着许多⼈⼒资源管理从业⼈员。
为此,有必要将当今国际上最流⾏的视窗统计软件SPSS应⽤于绩效考评之中。
在分析企业员⼯绩效⽔平时,由于员⼯绩效⽔平的指标很多,各指标之间还有⼀定的关联性,缺乏有效的⽅法进⾏⽐较。
⽬前较理想的⽅法是⾮参数统计⽅法。
本⽂将列举某企业的具体情况确定适当的考核标准,采⽤主成分分析以及聚类分析⽅法,⽐较出各员⼯绩效⽔平,从⽽为企业绩效管理提供⼀定的科学依据。
最后采⽤判别分析建⽴判别函数,同时与原分类进⾏⽐较。
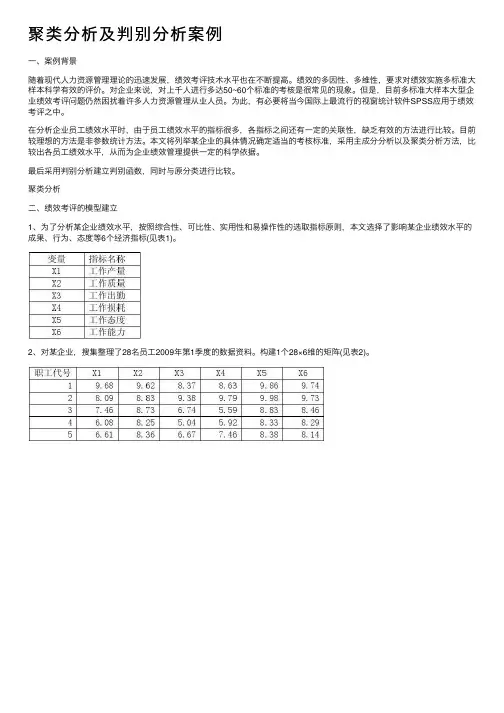
聚类分析⼆、绩效考评的模型建⽴1、为了分析某企业绩效⽔平,按照综合性、可⽐性、实⽤性和易操作性的选取指标原则,本⽂选择了影响某企业绩效⽔平的成果、⾏为、态度等6个经济指标(见表1)。
2、对某企业,搜集整理了28名员⼯2009年第1季度的数据资料。
构建1个28×6维的矩阵(见表2)。
3、应⽤SPSS数据统计分析系统⾸先对变量进⾏及主成分分析,找到样本的主成分及各变量在成分中的得分。
去结果中的表3、表4、表5备⽤。
表 5成份得分系数矩阵a成份1 2Zscore(X1) .227 -.295Zscore(X2) .228 -.221Zscore(X3) .224 -.297Zscore(X4) .177 -.173Zscore(X5) .186 .572Zscore(X6) .185 .587提取⽅法 :主成份。
构成得分。
a. 系数已被标准化。
4、从表3中可得到前两个成分的特征值⼤于1,分别为3.944和1.08,所以选取两个主成分。
根据累计贡献率超过80%的⼀般选取原则,主成分1和主成分2的累计贡献率已达到了83.74%的⽔平,表明原来6个变量反映的信息可由两个主成分反映83.74%。
全国各省经济的聚类分析摘要 (2)引言 (2)一聚类分析 (2)二聚类分析的优点 (2)三聚类分析相比较于其他分析方法而言 (2)实验方案 (3)1.1数据统计 (3)1.2聚类分析 (3)表1 (4)2结果分析与讨论 (5)表2 (5)表3 (6)表4 (6)表5 (7)图1 (8)总结 (8)小结 (9)参考文献 (9)摘要:改革开放以来,中国各省市在经济发展方面都取得了显著的成绩。
这篇论文利用SPSS软件对全国31个省、直辖市、自治区(浙江、湖南、甘肃除外)的主要经济指标进行聚类分析,将其经济分成4种类型,并对浙江、湖南、甘肃进行类型判别分析。
通过这两个方法对全国各省进行经济分类。
本文选取了7项经济指标作为决定经济类型的影响因素,各项数据均来自2010年国家统计年鉴。
分析结果表明:北京市和上海市为第一类经济类型;江苏省和山东省为第三类型;广东省为第四类经济;其他25个省、直辖市、自治区均属于第二类型。
关键词:聚类分析、经济类型引言:一聚类分析(cluster analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术。
聚类分析区别于分类分析(classification analysis) ,后者是有监督的学习。
它直接比较各事物之间的性质,将性质相近的归为一类,将性质差别较大的归入不同的类。
系统聚类分析又称集群分析,是聚类分析中应用最广的一种方法,它根据样本的多指标(变量)、多个观察数据,定量地确定样品、指标之间存在的相似性或亲疏关系,并据此连结这些样品或指标,归成大小类群,构成分类树状图或冰柱图。
二聚类分析的优点:聚类分析简单、直观;主要应用于探索性的研究,其分析的结果可以提供多个可能的解,选择最终的解需要研究者的主观判断和后续的分析;不管实际数据中是否真正存在不同的类别,利用聚类分析都能得到分成若干类别的解;聚类分析的解完全依赖于研究者所选择的聚类变量,增加或删除一些变量对最终的解都可能产生实质性的影响。
判别和聚类分析1判别和聚类分析1一、判别分析1.概念判别分析(Discriminant Analysis)是一种统计分析方法,主要用于研究如何根据已知的数据集来预测未知样本所属类别的方法。
判别分析的目标是找到一个分类函数,将数据集中的样本分为不同的类别,使得同类别内的样本尽可能相似,不同类别之间的样本尽可能不同。
2.方法判别分析的方法包括线性判别分析(Linear Discriminant Analysis,LDA)和二次判别分析(Quadratic Discriminant Analysis,QDA)。
线性判别分析通过找到一个线性变换将原始数据映射到低维空间中,最大化不同类别的类间离散度,最小化同一类别内的类内离散度。
二次判别分析则允许类别之间的协方差矩阵不同。
3.应用判别分析可以应用于各个领域的问题,例如医学诊断、金融风险评估和图像分类等。
在医学领域,判别分析可以通过对患者的症状和检测指标进行统计分析,预测患者是否患有其中一种疾病。
在金融风险评估中,判别分析可以根据企业的财务指标和市场环境数据,对企业的债务违约风险进行预测。
在图像分类中,判别分析可以通过从图像中提取特征,训练一个分类器来识别不同的物体和场景。
二、聚类分析1.概念聚类分析(Cluster Analysis)是一种无监督学习方法,主要用于将数据集中的样本分成若干个类别。
聚类分析的目标是找到一种合理的方式将数据样本划分为组内相似度高,组间相似度低的若干簇。
2.方法聚类分析的方法包括层次聚类(Hierarchical Clustering)和非层次聚类(Non-hierarchical Clustering)。
层次聚类通过构建树状结构将样本逐步合并或分裂,直到得到最终的簇划分。
非层次聚类则根据其中一种相似度度量,将样本分成预定的簇数。
3.应用聚类分析广泛应用于许多领域,例如市场细分、社交网络分析和推荐系统等。
在市场细分中,聚类分析可以根据消费者的购买行为和偏好将市场细分为不同的目标群体,从而制定对应的市场策略。
聚类分析与判别分析的比较聚类分析统计是比较各个事物间的性质,根据需要将性质相近的事物归为同一类,而将性质相差较大的归入不同的类。
它的本质是建立一种分类方法,他能够将一批样本数据按照他们性质上的亲密程度在没有先验知识的情况下自动进行分类。
聚类分析方法主要有两种:一种是快速聚类分析方法,一种是层次聚类分析方法。
层次聚类分析按其分类对象的不同分为Q型聚类分析它是根据被观测的样品的各种特征,将特征相似的样品归并为一类;R型聚类分析是根据被观测的变量之间的相似性,将其特征相似的变量归并为一类。
快速样本聚类适合聚成的类数已确定和大样本的聚类分析;而分层聚类则事先无法确定类别数,但给出的统计量可以帮助确定最好的分类结果。
后者对大样本分析受限制。
以下,我用《按三次产业分地区生产总值(2008年)》(来自国家统计局网站年度数据)通过快速聚类分析方法进行分类结果分析:从输出结果可以看出,当样本层次聚类分析成3个类时,样本的类归属情况:第一类包括7个省:北京、上海、安徽、福建、湖南、湖北、四川;第二类包含17个省:天津、山西、内蒙古、吉林、黑龙江、江西、广西、海南、重庆、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆;第三类包含4省:河北、辽宁、浙江、河南;第四类包含3个省:江苏、山东、广东判别分析是另一种处理分类分体的统计方法。
它是先根据已知类别的事物的性质,建立函数式,然后对未知类别的新事物进行判断以将之归入已知的类别中。
判别分析的内容十分丰富,按照已知分类的多少,分成两组判别喝多组判别;按照判别方法分为逐步判别和序贯判别;按照判别则分为距离判别、贝叶斯判别和费歇判别等。
通过聚类分析我们已经知道以上31个省的分类情况,现在将福建、江西、山东、河南四个省的聚类结果删除掉。
然后进行判别分析。
得出结果如上图,福建,江西,山东,河南四省的判别结果与之前分类结果一样。
典型判别式函数系数函数1 2 3第一产业.000 .002 .001第二产业.001 -.001 .000第三产业.000 .001 .000(常量) -3.744 -1.017 -.516非标准化系数由此图得出三个函数(X1,X2,X3分别为第一产业、第二产业、第三产业)D1=-3.744+0.001X2D2==1.017+0.002X1-0.001X2+0.001X3D3=-0.516+0.001X1通过聚类分析和判别分析,我们得到了31省的分类结果。
广东金融学院实验报告课程名称:附录:1、进行描述性统计量分析,对现价进行分位数分类程序:data lwh;set lwh;if price>0;run;procunivariate data=lwh;var price;run;运行结果:图1 输出现价分位数2、将人工分类做逐步判别分析的程序:data lwh;set lwh;if price<6.42then l=1;if price>6.42 and price<9.615then l=2;if price>9.615 and price<15.29then l=3;if price>15.29then l=4;run;data lwh;set lwh;drop price;run;procstepdisc data=lwh;class l;run;运行结果:图2逐步判别分析的剩余变量和剔除变量3、判别分析的程序:procdiscrim data=lwh outstat=newstat method=normal pool=yes list crossvalidate;class l;priorsproportional;var var1-var3 var5-var6 var8 var11-var19;run;运行结果:图3 人工分类剩余变量的判别分析结果4、聚类分析程序:procaceclus data=lwh out=ace p=0.03noprint;var var1-var3 var5-var6 var8 var11-var19;run;proccluster data=ace outtree=Tree method =wardcccpseudoprint=15;var var1-var3 var5-var6 var8 var11-var19;id code;run;proctree data=Tree out=new nclusters=4 graphics haxis=axis1 horizontal;height _rsq_;copy var1-var3 var5-var6 var8 var11-var19;id code;run;运行结果:图4聚类分析的结果图5 谱系聚类图5、根据聚类的分类进行逐步判别程序:procstepdisc data=new;class cluster;run;运行结果:图6聚类剩余变量的逐步判别6、对按聚类分类的逐步判别后的剩余变量,进行判别分析程序:procdiscrim data=new outstat=newstat method=normal pool=yes list crossvalidate;class cluster;priorsproportional;var var1-var3 var5-var6 var8 var14-var19;run;运行结果:图7 聚类分类的判别分析结果。
判别分析(Discriminant Analysis)一、概述:判别问题又称识别问题,或者归类问题。
判别分析是由Pearson于1921年提出,1936年由Fisher首先提出根据不同类别所提取的特征变量来定量的建立待判样品归属于哪一个已知类别的数学模型。
根据对训练样本的观测值建立判别函数,借助判别函数式判断未知类别的个体。
所谓训练样本由已知明确类别的个体组成,并且都完整准确地测量个体的有关的判别变量。
训练样本的要求:类别明确,测量指标完整准确。
一般样本含量不宜过小,但不能为追求样本含量而牺牲类别的准确,如果类别不可靠、测量值不准确,即使样本含量再大,任何统计方法语法弥补这一缺陷。
判别分析的类别很多,常用的有:适用于定性指标或计数资料的有最大似然法、训练迭代法;适用于定量指标或计量资料的有:Fisher二类判别、Bayers多类判别以及逐步判别。
半定量指标界于二者之间,可根据不同情况分别采用以上方法。
类别(有的称之为总体,但应与population的区别)的含义——具有相同属性或者特征指标的个体(有的人称之为样品)的集合。
如何来表征相同属性、相同的特征指标呢?同一类别的个体之间距离小,不同总体的样本之间距离大。
距离是一个原则性的定义,只要满足对称性、非负性和三角不等式的函数就可以称为距绝对距离马氏距离:(Manhattan distance)设有两个个体(点)X与Y(假定为一维数据,即在数轴上)是来自均数为μ,协方差阵为∑的总体(类别)A的两个个体(点),则个体X与Y的马氏距离为(,)X与总体(类别)A的距离D X Y=(,)为D X A=明考斯基距离(Minkowski distance):明科夫斯基距离欧几里德距离(欧氏距离)二、Fisher两类判别一、训练样本的测量值A类训练样本编号 1x 2xm x1 11A x 12A x 1A m x 221A x22A x2A m xA n1A An x 2A An xA An m x 均数1A x2A xAm xB 类训练样本编号 1x 2x m x1 11B x 12B x 1B m x 221B x22B x2B m xB n1B Bn x 2B Bn x B Bn m x 均数1B x2B xBm x二、建立判别函数(Discriminant Analysis Function)为:1122m m Y C X C X C X =+++其中:1C 、2C 和m C 为判别系数(Discriminant Coefficient ) 可解如下方程组得判别系数。
实验二聚类与判别实验项目名称:利用Matlab进行聚类和判别分析实验项目性质:普通实验所属课程名称:数学建模实验参考资料:实验计划学时:4一、实验目的:1、利用MATLAB进行聚类分析和判别分析;2、通过实际例题学习用聚类和判别分析解决相关简单的实际问题;3、理解判别分析误判率含义,应用判别模型进行预测。
二、实验内容2.1 聚类分析1、工厂产品问题(教材220页例题9.3);2、工人身高体重问题(教材239页习题9.1);2.2 判别分析1、雨天非雨天问题(教材231页例9.5);2、蠓的分类(教材234页);三、实验方法、步骤及结果分析简要提示3.1 基础知识一、聚类在MATLAB中通过pdist、linkage、dendrogram、cluster等函数来完成此种方法。
层次聚类的过程如下:1、相似性度量确定对象(实际上就是数据集中的每个数据点)之间的相似性,实际上就是定义一个表征对象之间差异的距离,例如最简单的平面上点的聚类中,最经常使用的就是欧几里得距离。
使用pdist来实现,具体用法如下:Y = pdist(X,distance)根据距离distance来计算X中各点之间的距离Y。
其中X为数据集,distance可以取为欧氏距离,马氏距离,切比雪夫距离。
对于具有M个点的数据集X,pdist之后的Y将是具有M*(M-1)/2个元素的行向量。
例1-1:Y=pdist(X)举例。
>> X=randn(6,2)X =-0.4326 1.1892-1.6656 -0.03760.1253 0.32730.2877 0.1746-1.1465 -0.18671.1909 0.7258>>plot(X(:,1),X(:,2),'bo') %画出X的散点图(图1)图1>>Y=pdist(X) %计算X的第一个点与与2-6点、第2点与3-6点,......距离Y =Columns 1 through 151.7394 1.0267 1.2442 1.5501 1.6883 1.8277 1.9648 0.54012.9568 0.2228 1.3717 1.1377 1.4790 1.0581 2.5092例子中X数据集可以看作包含6个平面数据点,pdist之后的Y是一个行向量,15个元素分别代表XC个元素的行向量。
的第1点与2-6点、第2点与3-6点,......这样的距离。
则Y为具有26注:(1)Y这样的显示虽然节省了内存空间,但对用户来说不是很易懂,如果需要对这些距离进行特定操作的话,也不太好索引。
MATLAB中可以用squareform把Y转换成方阵形式,方阵中<i,j>位置的数值就是X中第i和第j点之间的距离,显然这个方阵应该是个对角元素为0的对称阵。
>> squareform(Y)ans =0 1.7394 1.0267 1.2442 1.5501 1.68831.7394 0 1.8277 1.9648 0.54012.95681.0267 1.8277 0 0.2228 1.3717 1.13771.2442 1.9648 0.2228 0 1.4790 1.05811.5501 0.5401 1.3717 1.4790 02.50921.68832.9568 1.1377 1.0581 2.5092 0注:(2)pdist可以使用多种参数,指定不同的距离算法。
另外,当数据规模很大时,可以想象pdist产生的Y占用内存将是很吓人的,比如X有10k个数据点,那么X占10k*8*2Bytes=160K,这看起来不算啥,但是pdist后的Y会有10k*10k/2*8Bytes=400M。
因此,使用MATLAB的层次聚类来处理大规模数据,大概是很不合适的。
2、聚类树的产生确定好了对象间的差异度(距离)后,就可以用Z=linkage(Y)产生层次聚类树。
>> Z=linkage(Y) Z =3.00004.0000 0.22288.0000 10.0000 1.3717对于6个元素的X , Y 是1行6*(6-1)/2的行向量,Z 则是(6-1)*3的矩阵。
Z 数组的前两列是索引下标列,最后一列是距离列。
如上例中表示在产生聚类树的计算过程中,第3和第4点先聚成一类,他们之间的距离是0.2228,以此类推。
要注意的是,为了标记每一个节点,需要给新产生的聚类也安排一个标识,MATLAB 中会将新产生的聚类依次用6+1,6+2,....依次来标识。
比如第3和第4点聚成的类以后就用7来标识,第2和第5点聚成的类用8来标识,依次类推。
通过linkage 函数计算之后,实际上二叉树式的聚类已经完成了。
Z 这个数据数组不太好看,可以用dendrogram(Z)来可视化聚类树。
dendrogram(Z)注:(3) dendrogram 默认最多画30个最底层节点,当然可是设置参数改变这个限制,比如dendrogram(Z,0)就会把所有数据点索引下标都标出来,但对于成千上万的数据集合,这样的结果必然是图形下方非常拥挤。
3、聚类树的检验(Verifying the Cluster Tree )*初步的聚类树画完后,还要做很多后期工作的,包括这样的聚类是不是可靠,是不是代表了实际的对象分化模式,对于具体的应用,应该怎样认识这个完全版的聚类树,产生具有较少分叉的可供决策参考的分类结果呢?这都是需要考虑的。
MATLAB 中提供了cluster, clusterdata, cophenet, inconsistent 等相关函数。
cluster 用于剪裁完全版的聚类树,产生具有一定cutoff 的可用于参考的树。
clusterdata 可以认为是pdist,linkage,cluster 的综合,当然更简易一点。
cophenet 和inconsistent 用来计算某些系数,前者用于检验一定算法下产生的二叉聚类树和实际情况的相符程度(就是检测二叉聚类树中各元素间的距离和pdist计算产生的实际的距离之间有多大的相关性),inconsistent则是量化某个层次的聚类上的节点间的差异性(可用于作为cluster的剪裁标准)。
后面这些的理解,大概需要对聚类有一个更深刻更数学的认识。
在一个层次聚类树中,在原数据集中任何两个对象最终是某种程度上联结在一起。
联结的高度代表了包含这两个对象两个组之间的距离。
这个高度就是两个对象间的分类距离。
对于由linkage函数产生的聚类树,一种衡量其优劣的方式就是比较由linkage和pdist产生的距离。
如果聚类有效,在分类树中,对象的联结与距离向量中的对象将会具有强关联性。
Cophenet函数比较了这些值所在的两个集合并且计算它们的相关性,返回值称为分类相关系数,此值越接近1,说明对数据聚类的结果越能精确。
例如:图4 将20工厂的值赋给16和21工厂的聚类结果根据图4可见,聚类结果为:第一次计算两个样品的最小距离是1,所以把距离为1的点合成一类:{17,18,19},{12,13},{5,6,11},{7,8,9},{1,2}第二次计算两个类间的最短距离为2。
把距离不大于2的类归为一类,则得5个扩大的新类:{20,17,18,19},{5,6,11,3},{7,8,9,10}第三次计算两个类间的最小距离为2,则有新类{12,13,15},{1,2,3,4}第四次计算两个类间的最小距离为2.2361,则将所有的点(除16和21),归在四类中:{12,13,15,14},{1,2,3,4,5,6,11},{7,8,9,10},{17,18,19,20}二、判别能将数据模型进行分类的特征曲线称作分类器。
对于一种已知的分类器而言,源于训练数据。
然后基于此分类器对新的样本进行分类。
两个总体的判别法参数化的方法,例如判别分析—根据训练数据拟合出参数模型,然后代入新的数据对其进行分类。
非参数化的方法,如分类树的方法—使用其它的方式去确定分类器。
判别分析使用训练数据去估计关于预测变量的判别函数。
在预测空间中,判别函数确定不同类之间的界限。
1、距离判别法以G 1和G 2分别表示两总体,设它们是取值于R p 中的随机变量,它们的数学期望和协方差矩阵分别为11EG μ=,22EG μ=,11VarG S =,22VarG S =问题:设有一个样本x ∈R p,问x 属于总体G 1还是属于总体G 2?距离判别法是根据x 与G 1、G 2的距离决定x 的归属。
其原则是:若x 与G 1距离小,则x 属于G 1;若x 与G 2的距离小,则x 属于G 2。
即(ⅰ)如果1(,G )d x ≤2(,G )d x ,则判断1G x ∈; (ⅱ)如果2(,G )d x <1(,G )d x ,则判断2G x ∈。
其中,(,G )i d x 为马氏距离,即2(,G )i d x =(T 1)()i i i x S x μμ---,2,1=i[class,err,POSTERIOR] = classify(sample,training,group,type) 说明:sample —样本数据;training —训练数据集。
Classify 将训练集training 中的每行样本sample 数据进行分类, sample与training 必须是具有相同列数的矩阵; group —训练数据所对应的类集合; type —判别函数的类型;可选以下类型:(1)'linear' — 线性分类器,为缺省时默认值。
(2)'diaglinear' — 对角线性分类器,类似于 'linear', 但其具有一对角协方差矩阵估计 (naiveBayes classifiers).(3)'quadratic' — Fits multivariate normal densities with covariance estimates stratified by group.(4)'diagquadratic' — 类似于'quadratic',但具有一个对角协方差矩阵估计。
Similar to 'quadratic', but with a diagonal covariance matrix estimate (naive Bayes classifiers).(5)'mahalanobis' — 使用马氏距离及协方差估计。
返回值class —对sample 的分类结果;err —基于训练数据的误判率估计;POSTERIOR —后验概率矩阵的估计值,即已知第i 个样本观察值条件下,其来源于第j 各类的概率Pr(group j|obs i)。