六年级数学上册第四单元圆
- 格式:doc
- 大小:524.00 KB
- 文档页数:22

六年级上册数学第四单元《圆的周长》教学反思六年级上册数学第四单元《圆的周长》教学反思「篇一」[案例]师:用自己的话说一说什么是圆的周长。
(同桌间利用圆形物体互相指一指)师:对呀,圆是一个曲线图形。
你们有办法测量它的周长吗?生1:“滚动”——把实物圆(如硬币)放在直尺上滚动一周,所经过的长度即为这个圆的周长。
生2:“缠绕”——用棉线绕圆一周并打开,然后将棉线拉直,测量出它的长度就是这个圆的周长。
生3:我同意刚才两人的观点。
我还有一个建议:将一个圆纸片对折后再滚一滚或是用棉线绕一绕,把测量得出的数据再乘2就行了。
这样测量比较快。
生4:“剪圆”——沿着这个圆的边缘剪下一圈,越细越好,可以将这一圈近似地看成是一条线段,然后测出纸条的长度,即为圆的周长。
(学生根据自己的经验测量圆的周长,并进行演示。
)师:看来大家都有一个共同的愿望,把圆的周长曲线段转化成直的线段。
(板书:曲转化直)[点评]:在学生意犹未尽的时候,及时带领学生进行过程整理。
因为学生的体验一方面来自教师有意识的引导,另一方面是对经历过程所带来的情绪回味。
师:在显示生活中有许许多多大小不同的圆,如果每次测量圆周长都用大家提出的这些方法,你觉得怎样?有什么好主意吗?生:我觉得可以像其他平面图形长方形、正方形那样,研究出圆周长的计算的一般方法,这样就好办了。
[点评]:在矛盾冲突中,使学生感到“滚动”、“缠绕”等方法测量圆周长有一定的局限性。
甚至根本做不到。
从而有效地激发学生对圆周长计算公式的探究欲望,可以说是“水到渠成”。
师:你们认为圆周长与它的什么有关呢?生:我认为圆周长与它的直径有关。
通过观察,我们不难发现,直径越大的圆,它的周长也越长。
师:对呀,正方形的周长总是边长的4倍。
(出示图)猜猜看:圆周长会是直径的几倍呢?图示:生1:在这幅图中,正方形的边长与圆的直径相等,而圆正好套在正方形内,所以,我认为圆的周长小于直径的4倍。
生2:我还可以观察得出:因为圆周长的一半是打援直径的,所以我认为圆周长大于直径的2倍。

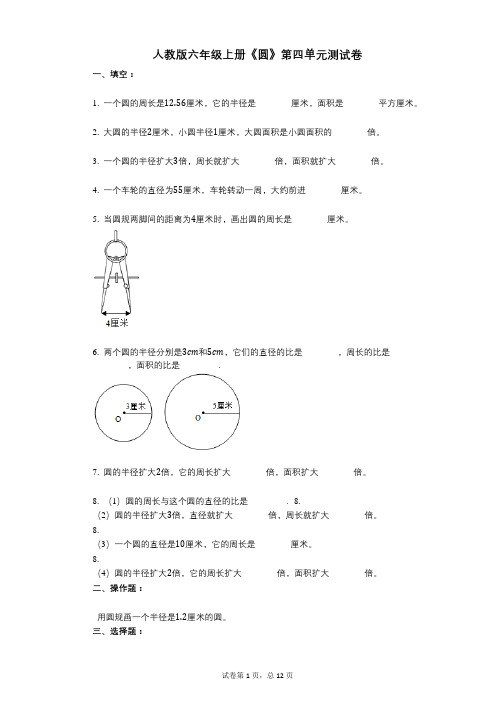
人教版六年级上册《圆》第四单元测试卷一、填空:1. 一个圆的周长是12.56厘米,它的半径是________厘米,面积是________平方厘米。
2. 大圆的半径2厘米,小圆半径1厘米,大圆面积是小圆面积的________倍。
3. 一个圆的半径扩大3倍,周长就扩大________倍,面积就扩大________倍。
4. 一个车轮的直径为55厘米,车轮转动一周,大约前进________厘米。
5. 当圆规两脚间的距离为4厘米时,画出圆的周长是________厘米。
6. 两个圆的半径分别是3cm和5cm,它们的直径的比是________,周长的比是________,面积的比是________.7. 圆的半径扩大2倍,它的周长扩大________倍,面积扩大________倍。
8. (1)圆的周长与这个圆的直径的比是________. 8.(2)圆的半径扩大3倍,直径就扩大________倍,周长就扩大________倍。
8.(3)一个圆的直径是10厘米,它的周长是________厘米。
8.(4)圆的半径扩大2倍,它的周长扩大________倍,面积扩大________倍。
二、操作题:用圆规画一个半径是1.2厘米的圆。
三、选择题:计算圆的面积,可以选择下面哪种方法()A.S=π(d÷2)2B.S=πr2C.S=π(C÷2π)2D.前三种都可以下面的图形只有两条对称轴的是()A.圆B.正方形C.等边三角形D.长方形在一个长10厘米、宽5厘米的长方形中画一个最大的圆,它的半径是()A.10厘米B.5厘米C.2.5厘米D.1.5厘米一个直径1厘米的圆与一个边长1厘米的正方形相比,它们的面积()A.圆的面积大B.正方形的面积大C.一样大D.无法比较一个钟表的分针长10厘米,从2时走到5时,分针针尖走过了()厘米。
A.31.4B.62.8C.188.4四、求下面阴影部分的面积.(单位:厘米)求下面阴影部分的面积。



第四单元圆一、基本概念1、圆心一个圆最中心的那一点,用大写字母O 表示(1) 圆心决定圆的位置。
(2) 圆心到圆上任意一点的距离都相等。
(3) 一张圆形纸片至少对折两次,就能找到圆心。
2、半径圆心到圆上任意一点的线段,用小写字母r 表示(1) 半径决定圆的大小。
(2) 在同一个圆里面,半径都相等。
(3) 在同一个圆里面,半径有无数条。
(4) 半径是直径的一半,即d 21r =3、直径通过圆心并且两端都在圆上的线段,用小写字母d 表示(1) 在同一个圆里面,直径都相等。
(2) 在同一个圆里面,直径有无数条。
(3) 直径是半径的两倍,即r 2d =(4) 在一个正方形内画最大的圆,圆的直径等于正方形的边长(5) 在一个长方形内画最大的圆,圆的直径等于长方形的宽二、使用圆规的步骤1、先确定圆心的位置和半径。
(1) 轴对称图形中,两条对称轴的交点就是中心点(2) 如果知道直径,那么直径的一半就是半径2、用直尺量出两脚之间的距离为半径。
(1) 量好后不能再改变两脚之间的距离3、把针尖放在圆心位置,保持针尖不动,旋转另一只脚一周,即可画出指定的圆。
(1)如果旋转圆规一周不顺手,可以保持圆规不动,旋转纸一周。
(2)如果旋转一周画出来的线条不清晰,可以多旋转几周加深线条。
三、轴对称图形1、轴对称图形沿对称轴对折之后,两边可以完全重合。
2、常见的轴对称图形以及它们的对称轴条数:(1)只有一条对称轴的图形:角、等腰三角形、等腰梯形、扇形、半圆(2)有2条对称轴的图形:长方形(3)有3条对称轴的图形:等边三角形(4)有4条对称轴的图形:正方形(5)有无数条对称轴的图形:圆、圆环【圆的对称轴就是直径】四、周长与面积1、圆周率ππ是一个无限不循环小数,一般取 3.14π≈。
我国数学家祖冲之是第一个把圆周率算出来的人。
2、圆的周长(1)圆的周长用大写字母C 表示,计算公式是πd πr 2C ==即圆的周长等于两倍的π乘以半径,也等于π乘以直径(2) 半圆的周长半圆的周长等于半个圆的周长加上直径,即r 2πr +3、圆的面积圆的面积用大写字母S 表示,计算公式是2πr S =4、周长与面积的关系(1) 在同一个圆中,半径扩大或缩小几倍,直径和周长就扩大或缩小几倍,而面积扩大或者缩小这个倍数的平方倍,例如:在同一个圆内,如果半径扩大3倍,那么直径和周长就扩大3倍,面积扩大9倍。
圆的周长和面积(一)单元教育目标1、经过操作,认识圆的周长与直径的比为定值;探究并掌握圆的周长和面积公式,能运用公式解决简单的问题。
2、在察看、操作、推理活动中,发展合情推理能力,能进行有条理地思虑,能比较清楚地表达自己思虑的过程与结果。
3、能探究剖析和解决问题的有效方法,能表达解决问题的思路和方法,加强应企图识,提升实践能力。
4、踊跃参加数学活动,获取探究同面积公式的经验,在运用圆周长和面积知识解决问题的过程中,认识数学的价值。
(二)单元教材说明本单元内容是在学生认识了圆,掌握了长方形、平行四边形、三角形等面积计算公式,拥有必定探究面积公式经验的基础上学习的。
主要内容有:探究圆的周长公式,解决和圆周长有关的实质问题,探究圆的面积公式,解决和圆面积有关的实质问题,环形面积。
圆的周长和面积是小学阶段图形与几何部分的重要内容,《数学课程标准》提出的详细要求是:经过操作,认识圆的周长与直径的比为定值,掌握圆的周长公式;探究并掌握同的面积公式,并能解决简单的实质问题。
解读课程内容的上述要求,第一突出了数学学习的操作性和探究性,重申让学生经历探究圆周长和面积公式的过程。
此外,突出数学的应用,重申停决简单的实质问题。
本单元教材在设计思想和内容编排上有以下特色:1、让学生经历圆周长和圆面积公式探究的全过程。
圆的周长和面积公式是本单元的中心知识点和研究解决问题的生长点,让学生经历圆周长和面积公式的形成过程,有益于学生理解、掌握计算公式,并获取建构数学模型的活动经验。
教材在安排探究圆的周长和面积公式时,都设计了四个层面的活动。
让学生经历由个别到一般,由感性经验到理性推导的全过程。
(1)探究圆的周长的过程有以下四步:第一,让学生利用转动法、环绕法等自主丈量硬币的周长,并计算周长除以直径,一方面获取丈量圆的周长的活动经验,另一方面获取周长除以直径的个体数据。
第二,小组合作,分别丈量三个大小不一样的圆形物件的周长和直径,并计算周长除以直径,为概括圆周率供给数据。
六年级数学上册第四单元知识点整理知识点认识圆形
1、圆的定义:圆是由曲线围成的一种平面图形。
2、圆心:将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心。
一般用字母o表示。
它到圆上任意一点的距离都相等.
3、半径:连接圆心到圆上任意一点的线段叫做半径。
一般用字母r表示。
把圆规两脚分开,两脚之间的距离就是圆的半径。
4、直径:通过圆心并且两端都在圆上的线段叫做直径。
一般用字母d表示。
直径是一个圆内最长的线段。
5、圆心确定圆的位置,半径确定圆的大小。
6、在同圆或等圆内,有无数条半径,有无数条直径。
所有的半径都相等,所有的直径都相等。
7.在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的1/2。
用字母表示为:d=2r或r=d/2
8、轴对称图形:
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
折痕所在的这条直线叫做对称轴。
9、长方形、正方形和圆都是对称图形,都有对称轴。
这些图形都是轴对称图形。
10、只有1一条对称轴的图形有:角、等腰三角形、等腰梯形、扇形、半圆。
只有2条对称轴的图形是:长方形
只有3条对称轴的图形是:等边三角形
只有4条对称轴的图形是:正方形;
有无数条对称轴的图形是:圆、圆环。