卷积积分

格式：ppt
大小：727.50 KB
文档页数：28

下载文档原格式

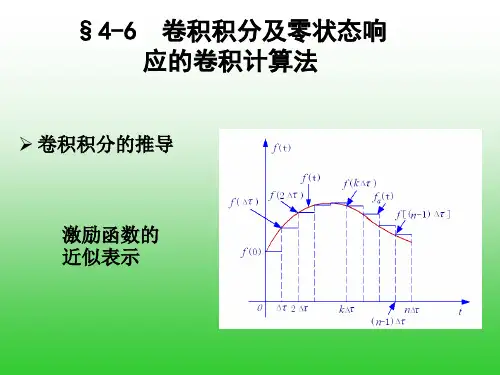
卷积积分及零状态响应的卷积计算法.

t
e RC
RCT
T RC t
e RCT 0
RC T RC
(t 0)
u0T T RC
e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积，实质上是求一个新函数
f()h(t)在由0到t的区间内的定积分。根据定积分的几何意义，函数在0到t区间内的定积分值，决定于被积函数f()h(t)的曲线在该区间内与轴之间所限定的面
§4-6 卷积积分及零状态响应的卷积计算法
➢ 卷积积分的推导
激励函数的近似表示
f (t) fa (t) f (0)ε(t) ε(t )
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
解： [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解：用卷积积分公式求uC(t)，应先求冲激响应
如按
t
r(t) h( ) f (t ) d h(t) f (t)
0
当 0<t <1 时
计算。
r(t ) te ε( )d t e d 1 et
0
0
当 t >1时
r(t ) t e ε( )d t 1
t e d e(t1) et t 1 返回
注意ቤተ መጻሕፍቲ ባይዱ分上、下限

卷积分

-T0
T0 h(-T0/2- τ)
-T0 -2T0 0 2T0 A2
T0
-T0
T0
卷积与相关
（7） t= -T0时，y( -T0)=A T0
2
x(t)
y(t) 2A2T0
-T0
T0 h(-T0- τ)
-T0 -2T0 0 2T0 A2
T0
-T0
T0
卷积与相关
x(t)
（8） t= -3T0/2时，y( -3T0/2)=3A2T0/2
-T0 -2T0 0 2T0 A2
T0
-T0
T0
卷积与相关
x(t)
（5） t= 2T0时，y(2T0)=0
y(t) 2A2T0
-T0
T0 h(T0/2- τ)
-T0 -2T0 0 2T0 A2
T0
-T0
T0
卷积与相关
（6） t= -T0/2时，y( -T0/2)=3A T0/2
2
x(t)
y(t) 2A2T0
x(t)
(1)反折；反折；反折 (2)平移；平移；平移
0 t (4)积分
h(t)
(3)相乘；相乘；相乘 (4)积分。积分。积分
t
0
t (1) (1)反折
x(t)
h(-τ)
0 x(t) h(t1 -τ)
0
τ
(2)平移
(3)相乘
h(t1 -τ)
tτ
00
0
τ
卷积与相关
4 含有脉冲函数的卷积 • 设 h(t)=[δ(t-T)+ δ(t+T)] • 卷积为
卷积与相关
• 例三角脉冲频谱计算
x(t) h(0-τ)

第二章 (4)卷积积分的性质

f 1 (t )
f 2 (t )
2
1
0
2
0 1
1
2 3
t
1
3
t
解法一: 解法一:图示法
f 1 (τ
t <1 ,
)
f (t ) = 0
2
0
1
2 3
τ
f 2 (t τ
t2
)
1
t 0
1
τ
解法一: 解法一:图示法
f 1 (τ
t <1 ,
)
t
f (t ) = 0
1< t < 2 ,
f (t ) = ∫ 2dτ = 2(t 1)
(2) e ε(t + 3) ε(t 5) 2t e ε (t + 3) ε (t 5) ∞ 2τ = ∫ e ε (τ + 3) ε (t τ 5)dτ ∞
2t
=∫t 53e2τ1 2(t 5) 6 e = e 2 6 1 2( t 2) = e 1 e 2
[
1 2τ dτ = e 2
' ∞ ∞
上式称为杜阿密尔积分. 上式称为杜阿密尔积分. 杜阿密尔积分其物理含义为: 其物理含义为:LTI系统的零状态响应等于激励的系统的零状态响应等于激励的
f ' (t )与系统的阶跃响应 g(t )的卷积积分. 的卷积积分. 导数
例2.4-4 求图示函数 f1(t ) 与 f2 (t ) 的卷积 f (t ) .
若f (t ) = f1(t ) f2(t ),则 f1(t t1 ) f2(t t2 ) = f1(t t2 ) f2 (t t1 ) = f (t t1 t2 )
推广4 推广

Z2.14 卷积积分的图解法

2
Xidian University, ICIE. All Rights Reserved
2.3 卷积积分
第二章连续系统的时域分析
例1 f (t), h(t) 如图，求yzs(t)= h(t) * f (t) 。 f (-τ ) f ( τt )
解:
h(t)函数形式复杂, 换元为h(τ)； f (t)换元为 f (τ)
2
② 0≤t ≤1时 ③ 1≤t ≤2 时
yzs (t)
t 1 d 1 t2
02
4
yzs (t)
t 1 d 1 t 1
t1 2
24
0 t t-11 tt-1 2 3 t yf (t )
④ 2≤t ≤3时
yzs (t)
2 1 d 1 t2 1 t 3
t1 2
4 24
f (τ)反折→ f (-τ)平移t f(t -τ) ① t < 0时 , f (t -τ→)向左移
f ( t -τ) h(τ) = 0，故 yzs(t) = 0 t>0 时, f (t -τ)向右移
f (t -τ ) t-1 t
01
τt
1 h ( tτ ) 2
பைடு நூலகம்
0
2
t-1 t t-1 t 2
τt
h(τ )f (t -τ ) 1
例2 f1(t), f2(t)如图，已知 y(t) = f1(t)* f2(t)，求y(6) =？
解：
y(6)
f1( )
f2 (6
) d
4
Xidian University, ICIE. All Rights Reserved
2.3 卷积积分
y(6)

通信技术概论3.4卷积积分的物理解释和性质2012

f (t ) * (t t 0 ) (t t 0 ) * f (t ) f (t t0 )
三、卷积积分的应用
(t )
e(t) r(t) r ( t ) e ( t ) * h( t )
即
线性网络零状态
t
h(t)
r (t ) e( )h(t )d
卷积积分
一、卷积积分(Convolution)的定义定义：设 f1(t)， f2(t) t < 0 均为零
f1 (t ) * f 2 (t ) f1 ( ) f 2 (t )d
t 0
二、卷积积分的性质性质1
f1 ( t ) * f 2 ( t ) f 2 ( t ) * f 1 ( t )
0
物理解释: 将激励 e(t)看成一系列宽度为，高度为 e(k )矩形脉冲叠加的。
e(t )
e(0)
o
2
k (k+1)
t
e(t ) e(0)[ (t ) (t Δ )] e(Δ )[ (t Δ ) (t 2Δ )]
e(kΔ ) p(t kΔ ) Δ
k 0
k 0
响应 r (t ) e(k ) hp (t k )
当e(t )分割得足够细即N ,
激励 e( t ) lim
N
e(kΔ ) p(t kΔ ) Δ
k 0
N
(t )
冲激
脉冲
响应 r ( t ) lim e( kΔ )hp ( t kΔ )Δ
积分
N k 0
N
脉冲响应
h(t )
冲激响应

卷积积分公式

卷积积分公式
卷积积分公式是一种数学运算，用于计算两个函数的卷积。

卷积是一种线性运算，用于描述两个函数之间的关系。

设有两个函数f(x)和g(x)，其卷积定义为：
(f * g)(x) = ∫f(t)g(x-t)dt
其中*表示卷积运算符，∫表示积分运算。

这个公式可以理解为，在函数g(x)上取一个滑动窗口，窗口的大小为函数f(x)的长度，然后计算窗口内两个函数的点积，并将结果在x上求和作为卷积结果。

卷积积分公式可以应用于信号处理、图像处理、物理学等领域，用于分析信号的频率特性、图像的模糊效果等。

卷积积分及其性质 ppt课件

d dx
(t)是奇函数 [ (x t)] f (x) d x [ f (t)] f (t)
第2-15页
PPT课件
15
■
©西安电子科技大学电路与系统教研中心
信号与系统电子教案
2.4 卷积积分的性质
3. f(t)*ε(t)

t
f ( ) (t ) d f ( ) d
¥
ò yzs (t) =f (t) * h(t) =
et [6 e- 2(t- t )- 1]e(t - t ) d t
-?
当t <τ，即τ> t时，ε(t -τ) = 0
蝌t
yzs (t) =
et [6 e- 2(t- t )- 1]d t =
-?
t
(6 e- e2t 3t - et ) d t
?
(t)
t0
)
f
(
t
)
d
t

f (t0)

'(t) f (t) d t f '(0)

PPT课件
(t
t0 )
f
(t) d t

f

(t0 )
16
第2-16页
■
©西安电子科技大学电路与系统教研中心
信号与系统电子教案
2.4 卷积积分的性质
三、卷积的微积分性质
1.
dn dtn
第2-11页
PPT课件
11
■
©西安电子科技大学电路与系统教研中心
信号与系统电子教案
2.4 卷积积分的性质
下面讨论均设卷积积分是收敛的（或存在的）。

卷积积分的运算

§2.5 卷积积分的运算和图解
y(t) x(t) h(t) x( )h(t )d
1）将x(t)和h(t)中的自变量由t改为，成为函数的自变量； 2）把其中一个信号翻转、平移；
h( ) 翻转h( ) 平移th(( t)) h(t )
3）将x() 与h(t )相乘；对乘积后的图形积分。
例11：画出下列系统的模拟图
y(t) 5 y(t) 3 y(t) 3x(t) x(t)
例：引入辅助函数q(t)
q(t) 5q(t) 3q(t) x(t) 利用微分特性法 y(t) 3q(t) q(t)
q(t) x(t) 5q(t) 3q(t)
例12：根据系统的模拟图写出其微分方程模型
et
d
r t
d
et
rt
et
rt
et
T rt
rt de(t)
dt
t
r(t) e(t)dt
rt et rt et T
例10：试用系统模拟图来表示下列方程所描述的LTI系统
a2 y(t) a1 y(t) a0 y(t) b2 x(t) b1 x(t) b0 x(t) a2 y(t) b2 x(t) b1 x(t) b0 x(t) a1 y(t) a0 y(t)
y(t )
1 a2
[b2 x(t )
b1 x(t )
b0 x(t )
a1
y(t)
a0
y(t )]
y(t )
1 a2
[b2 x(t )
b1 x(1) (t )
b0 x(2) (t ) a1 y(1) (t ) a0 y(2) (t )]
根据该式，可直接画出系统模拟图
y(t)

微积分讲座---Z2.13 卷积公式

f1(t) * f2 (t)
f1( )
f2 (t
)d
e ( ) (t )d
e (t- )d 0
[ t e d ] (t) 0
e t (t) 0
(1 et ) (t)
4
h(t)
LTI系统零状态
由时不变性： δ(t-τ)
h(t-τ)
由齐次性：f (τ)δ(t-τ)
f (τ) h(t-τ)
yzs(t)?
由叠加性：
f (τ)δ (tτ )dτ ǁ
f (τ ) h (t τ )d τ ǁ
f (t)
yzs (t)
y zs (t )
f ( )h(t ) d 卷积积分
量，t为参变量。结果仍为t 的函数。可演变其他上下限.
yzs (t)
f ( )h(t ) d f (t) * h(t)
3
2.3 卷积积分
第二章连续系统的时域分析
例1：f1 (t) =e-tε(t) ， f2 (t) = ε(t)，求f (t) = f1 (t)* f2 (t)。
解： f (t)
2
2.3 卷积积分
第二章连续系统的时域分析
[定义] 卷积积分
已知定义在区间(–∞,∞)上的两个函数f1(t)和f2(t)，则
定义积分
f (t)
f1(
)
f2 (t
)d
为f1(t)与f2(t)的卷积积分，简称卷积；记为 f(t)= f1(t)*f2(t)
注意：积分是在虚设的变量τ下进行的，τ为积分变
2.3 卷积积分
知识点Z2.13
第二章连续系统的时Байду номын сангаас分析
卷积公式
主要内容：

拉普拉斯逆变换卷积积分

拉普拉斯逆变换卷积积分
拉普拉斯逆变换卷积积分是一种常见的数学运算方法，用于求解
拉普拉斯变换后函数的逆变换。

它可以通过卷积积分的方式来实现。

具体来说，设函数F(s)的拉普拉斯变换为F(s)=L[f(t)]，其中
f(t)为原函数。

则拉普拉斯逆变换卷积积分的数学表达式为：
f(t) = (1/2πi)∫[c-i∞,c+i∞]e^(st)F(s)ds
其中，c为一个实数，需要满足所有F(s)的奇点都位于c的右半
平面内。

拉普拉斯逆变换卷积积分的求解过程较为复杂，需要利用留数定理、快速变换等方法。

首先，需要找到F(s)在右半平面内的奇点，并
计算其留数；然后，通过留数定理计算积分路径上的积分结果；最后，利用卷积公式将各个奇点的贡献加和得到最终的逆变换结果f(t)。

拉普拉斯逆变换卷积积分在信号处理、电路分析等领域有广泛的
应用。

通过该方法，可以将复杂的拉普拉斯变换后的函数转化为原始
的时域函数，使得问题求解更加方便和直观。

卷积积分介绍

h(t)
(1) 1
O
(1) t
g(t)
1
O12 1
g(t)f(1)(t)h(1)(t)
t 3 2t
t 3
0t 1 1t 2 2t 3
3 t
注意
28
注意
当f1(t)
t df1(t)dt时, dt
f 1 ( t) f 2 ( t) f 1 ( t) f 2 ( 1 )( t)
例 sg t： n t
系统并联运算
3．结合律
f ( t ) f 1 ( t ) f 2 ( t ) f ( t ) [ f 1 ( t ) f 2 ( t )]
系统级联运算
22
系统并联
f 1 ( t ) [ f 2 ( t ) f 3 ( t ) f ] 1 ( t ) f 2 ( t ) f 1 ( t ) f 3 ( t ) 系统并联，框图表示：
一般数学表示： g(t) f1()f2(t)d 信号无起因时： g(t) f()h(t)d
(4)卷积是数学方法，也可运用于其他学科。
(5)积分限由 f1(t),f2(t)存在的区间决定，即由
f1()f2(t)0的范围决定。
20
总结
求解响应的方法：时域经典法：完全解=齐次解 + 特解双零法：
: 信号作用的时刻，积分变量
从因果关系看，必定有 t
(2)分析信号是手段，卷积中没有冲激形式，但有其内容；
f() 是h(t-)的加权，求和
即d f() 是h(t-)的加权，积分
(t-)的响应
19
(3)卷积是系统分析中的重要方法，通过冲激响应h(t)建立了响应r(t)与激励e(t)之间的关系。
零输入响应：解齐次方程，用初（起）始条件求系数；

关于分段函数的卷积积分形式

关于分段函数的卷积积分形式分段函数卷积积分是一种分段函数和卷积积分的相结合的算法，用于在数学计算中求解分段函数形式的表达式。

一般来说，如果表达式中有多个不同的参数的话，分段函数的表达式可能占用很多空间，因此，使用卷积积分技术将会有很大的帮助。

一. 基本概念1）定义：分段函数卷积积分（Convolution Integral for Piecewise Functions）是指把若干个分段函数按变量先后顺序单调叠加，形成一个完整的函数，并将此函数应用卷积积分技术来求其数值积分。

2）特点：分段函数卷积积分技术具有减少计算量、求解精度高等优点，可以有效地求解分段函数形式的表达式的数值积分。

二. 其它表述1）几何说明：分段函数卷积积分技术可以由两个步骤组成，即：一.把分段函数按变量先后顺序单调叠加；二.采用卷积积分来求和这些单调叠加后的函数。

2）典型应用：分段函数卷积积分技术常用于对若干个分段函数变量的累积，比如将多个平面区域内的各种数据累加到一起。

此外，还可用于检测各种复杂类型的信号，进而确定信号是否有规律性或有意义的起伏趋势。

三. 工程实际1）分段函数卷积积分技术常用在工程领域，比如用于数控机床程序控制、汽车传感器数据处理等；如能够恰当地把多种分段函数整合成一个实现特定功能的连续函数，便能大大减少计算量，提高控制系统的运算效率。

2）此外，分段函数卷积积分技术还可用于解析控制系统本身的特性，例如，在不确定条件下，可用于判断控制系统的稳定性，以及寻求系统的相应参数。

四. 优缺点1）优点：分段函数卷积积分技术可以将表达式中多个分段函数计算简化，计算量少；求解准确，结果可靠；相对比较容易实现；稳定性好。

2）缺点：分段函数卷积积分技术有一定的适用范围，应用时需要先解析分段函数，当分段函数数量较多时，计算成本较高。

卷积和积分运算

卷积和积分运算卷积和积分运算先看到卷积运算，知道了卷积就是把模版与图像对应点相乘再相加，把最后的结果代替模版中⼼点的值的⼀种运算。

但是，近来⼜看到了积分图像的定义，⽴马晕菜，于是整理⼀番，追根溯源⼀下吧。

1 卷积图像1.1 源头⾸先找到了⼀篇讲解特别好的博⽂，原⽂为：贴过正⽂来看：---------------------------------------------------------------------------------------------------------------信号处理中的⼀个重要运算是卷积.初学卷积的时候,往往是在连续的情形, 两个函数f(x),g(x)的卷积,是∫f(u)g(x-u)du 当然，证明卷积的⼀些性质并不困难，⽐如交换，结合等等，但是对于卷积运算的来处，初学者就不甚了了。

其实，从离散的情形看卷积，或许更加清楚，对于两个序列f[n],g[n],⼀般可以将其卷积定义为s[x]= ∑f[k]g[x-k] 卷积的⼀个典型例⼦,其实就是初中就学过的多项式相乘的运算, ⽐如(x*x+3*x+2)(2*x+5) ⼀般计算顺序是这样, (x*x+3*x+2)(2*x+5) = (x*x+3*x+2)*2*x+(x*x+3*x+2)*5 = 2*x*x*x+3*2*x*x+2*2*x+ 5*x*x+3*5*x+10 然后合并同类项的系数, 2 x*x*x 3*2+1*5 x*x 2*2+3*5 x 2*5 ---------- 2*x*x*x+11*x*x+19*x+10 实际上,从线性代数可以知道,多项式构成⼀个向量空间,其基底可选为 {1,x,x*x,x*x*x,...} 如此,则任何多项式均可与⽆穷维空间中的⼀个坐标向量相对应, 如,(x*x+3*x+2)对应于 (1 3 2), (2*x+5)对应于 (2,5). 线性空间中没有定义两个向量间的卷积运算,⽽只有加法,数乘两种运算,⽽实际上,多项式的乘法,就⽆法在线性空间中说明.可见线性空间的理论多么局限了. 但如果按照我们上⾯对向量卷积的定义来处理坐标向量, (1 3 2)*(2 5) 则有 2 3 1 _ _ 2 5 -------- 2 2 3 1 _ 2 5 ----- 6+5=11 2 3 1 2 5 ----- 4+15 =19 _ 2 3 1 2 5 ------- 10 或者说, (1 3 2)*(2 5)=(2 11 19 10) 回到多项式的表⽰上来, (x*x+3*x+2)(2*x+5)= 2*x*x*x+11*x*x+19*x+10 似乎很神奇,结果跟我们⽤传统办法得到的是完全⼀样的. 换句话,多项式相乘,相当于系数向量的卷积. 其实,琢磨⼀下,道理也很简单, 卷积运算实际上是分别求 x*x*x ,x*x,x,1的系数，也就是说，他把加法和求和杂合在⼀起做了。

卷积积分辐射

卷积积分辐射卷积积分辐射是一种基于辐射定理的数学方法，它可以用于计算电磁波在各种媒质中传播时的特性。

下面将从卷积积分的定义、使用场景、计算过程、实际应用等几个方面来探究卷积积分辐射的知识点。

一、定义卷积积分是一种数学运算，其定义为：在一定区间内，将两个函数对应点相乘后再积分，在不同的区间内进行求和。

在信号分析、图像处理、通信系统等领域里，卷积积分常常被用于描述传递现象。

二、使用场景卷积积分辐射是一种特殊的辐射问题解决方法，广泛应用于电磁波理论中。

例如，我们可以用卷积积分辐射来计算天线辐射的特性，或者来估计视频图像的处理时间等。

三、计算过程计算卷积积分辐射的步骤如下：1.建立场点源等效表达式首先，我们需要确定场点源的位置和方向。

接着，将场点源表示为一个等效的体磁流源和体电流源的线性组合形式，用电流和磁流耦合方程计算出两个等效源的数学表达式。

2.建立源点场等效表达式由于卷积积分中积分变量为源的坐标，且电磁波传播是双向的，因此需要将场点源翻转过来，变成源点场。

然后，将源点场表示为一个等效的体电流源和体磁流源的线性组合形式，用电流和磁流耦合方程计算出两个等效源的数学表达式。

3.进行积分计算利用卷积定理和极坐标变换等方法，求出场点源在半径为r处的辐射磁场和电场，最终得到辐射方向图和功率方向图等。

四、实际应用卷积积分辐射在实际应用中有很多方面，例如计算天线辐射、磁盘阵列成像、雷达信号处理等。

此外，在计算机辅助工程设计、化学热力学、生物医学等领域里，卷积积分辐射也有广泛的应用。

综上所述，卷积积分辐射作为一个数学方法，可能相对抽象、高端，不过在电磁波理论的研究、天线辐射的计算中等应用方面扮演着重要的角色。

同时，卷积积分辐射也启示我们，通过先进数学工具的运用，可以更优美地解决工程实践的问题。

02-1 卷积积分的代数性质课件

通信原理
卷积积分的代数性质
2、分配律
f1(t) f2(t) f3(t) f1(t) f2(t) f1(t) f3(t)
系统的并联运算：子系统并联时，总系统的冲激响应等于各子系统的冲激响应之和。
y(t ) f (t ) h1(t ) f (t ) h2 (t )
y(t) f (t) h1(t) h2(t)
f (t ) h1(t ) f (t ) h2(t )
通信原理
卷积积分的代数性质
3、结合律
f1(t) f2(t) f3(t) f1(t) f2(t) f3(t)
系统的级联运算：
y(t ) f (t ) h1(t ) h2 (t )
y(t) f (t) h(t) f (t ) h1(t ) h2 (t )
谢谢！
通信原理卷积积分的代数来自质主讲人：吉利萍通信与信息工程学院
1
1
通信原理
卷积积分的代数性质
卷积积分是一种数学运算，它有许多重要的性质（或运算规则），灵活地运用其性质能简化卷积运算。下面讨论均设卷积积分是收敛的（或存在的）。
卷积积分的代数性质：
卷积积分满足乘法的三大定律： 1、交换律
f1(t) f2(t) f2(t) f1(t)
子系统级联时，总系统的冲激响应等于各子系统的冲激响应的卷积。
通信原理
卷积积分的代数性质
例：图中子系统 h1(t)是一LTI系统。当激励 f1(t) (t) 时，该子系统的零状态响应为 y1(t) (t) 2 (t 1) (t 2) 。若给定激励为 f2(t) (t) (t 2)，求下图所示系统的零状态响应 y2(t) 。
解：利用阶跃响应和冲激响应的关系，有子系统的冲激响应：h1(t ) y1(t ) (t ) 2 (t 1) (t 2)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

τ
∴yzs (t) = ∫ f (τ)h(t τ)d τ
t0
t
2.物理意义: 2.物理意义: 物理意义 LTIS在任意时刻 LTIS在任意时刻t对任意激励的零状态响应等于从激励函在任意时刻t 数开始作用的时刻( 数开始作用的时刻( = t0 到指定时刻(τ = t 区间内,无 )区间内, τ )到指定时刻( 穷多个幅度不同,连续出现的冲击响应的总和. 穷多个幅度不同,连续出现的冲击响应的总和. 这就是说,输入f 这段时间内电路的连续作用, 这就是说,输入f(t)从t=t0到t 这段时间内电路的连续作用, 可以用一序列冲击信号对电路激励去等效, 可以用一序列冲击信号对电路激励去等效,每个冲击信号
∞ ∞ ∞ ∞
∞
= ∫ f1(λ)[∫ f2(τ)] f3(t τ λ)dτ]dλ
∞ ∞
= f1(t)[ f2(t) f3(t)]
卷积的微分和积分: 二.卷积的微分和积分: 卷积的微分和积分 1.微分: 微分: 微分
d df2(t) df1(t) [ f1(t) f2(t)] = f1(t) = f2(t) dt dt dt
k=∞
yn (t) = ∑ f (kτ)τhn (t kτ) = ∑ f (kτ)hn (t kτ)τ
n=∞
和→积分当 (τ →0)时,τ → dτ, kτ → dτ , 求
任意信号:
f (t) = ∫ f (τ)δ(t τ)d τ
∞
∞
任意信号产生的零状态响应:
yzs (t) = ∫ f (τ)h(t τ)d τ
则有:
df1(t) t ∫ f2(λ)dλ y(t) = f1(t) f2(t) = ∞ dt
推论:
y (t) =[ f
(i)
( j) 1
(t) f
(i j) 2
(t)]
例:
dδ(t) t U(t)*U(t) = *∫ U(t)dt =δ(t)*tU(t) = tU(t) ∞ dt
三,与冲击函数或阶跃函数的卷积 1,与冲击函数的卷积:
∞ t
t
= f2(t)∫ f1(λ)dλ
∞
∫
t
∞
[ f1(λ)f2(λ)]dλ = ∫ [∫ f1(τ) f2(λ τ)dτ]dλ
∞ t ∞
t
t
= ∫ f1(τ)[∫ f2(λ τ)dλ]dτ
∞ ∞
t
= f1(t)∫ f1(λ)dλ
∞
t
3. 高阶导数和多重积分设:
y(t) =[ f1(t) f2(t)]
1 ≤ t <1 2
t-2
t
0 h(t τ ) -1/2 1 t t (c) 1 ≤ t ≤ 3 f( τ ) h(τ )
τ
f( τ )
h(t τ )
f( τ )
h(t τ )
15/16 9/16 -1/2 0 1 3/2 2 (f) t
-1/2 0 t-2 1 (d)
t
t
τ
0 -1/2 1
t-2 t
5.4 电路系统对任意激励的零状态响应- 的零状态响应-卷积积分
5.4.1 卷积积分定理: 卷积积分定理:
1.卷积积分定理:任一LTIS对任意激励信号的零状态响应卷积积分定理:任一对任意激励信号f(t)的零状态响应卷积积分定理对任意激励信号应该等于该激励信号与电路系统冲击响应的卷积积分. 应该等于该激励信号与电路系统冲击响应的卷积积分.即:
其余
f(t)
t<0 t>0
A 0 a
B
h(t)
Be-αt
0 t
t
(a)
f(t) A 0 a τ A 0
( b)
f(t)
(C)
( d)
a t
τ
(2)计算卷积积分:
y(t) = f (t)*h(t)
ⅰ.t<0, f (τ)和 (t τ) 无重叠. h ⅱ.0≤t≤a,tl1=0, tl2=-∞,选tr1=a, tr2=t
f (t)
R = 6
iL(t)
L= 2H
L diL(t) +iL(t) =δ(t) R dt R t R L ∴h(t) = e U(t) =3e3tU(t) L
(2)卷积求yzs(t) )卷积求y
τ iL(t) = ∫ f (t τ)h(τ)d = ∫ 2e(tτ ) 3 3τ dτ e
0 0
f (t)*δ(t) = f (t)
证明:
抽样性
f (t)δ(t) = ∫ f (τ)δ(t τ)dτ
∞ ∞
∞
= ∫ f (τ)δ(τ t)dτ
∞
1 t-2
1 -2 0 (c)
τ
0 t (d)
τ
(1)褶叠: (将横轴t→ (2)平移 (3)相乘积分
τ , h(τ) 对褶过去)
(2). 卷积积分积分限的确定原则: 若函数 f1( )和2(t τ) 的非零值左边界(即函数不为0的最小的非零值左边界(即函数不为0 τ f 值)分别为t 值)分别为tl1和tl2,其非零值右边界(即最大的 τ 值)分别积分下限取它们左边界的最大者,而积分上限取它们右边界中的最小者.
为tr1和tr2,则积分下限为max[tl1,tl2],上限为min[tr1,tr2].即τ ,则积分下限为max[t ,上限为min[t
h(t τ )
t t-2
f(τ )
h(t τ )
f( τ )
f( τ )
-1/20 1 (a) ∞ < t ≤
1 2
τ
t
τ
t-2 -1/20 t 1 (b)
∞ ∞
τ t λ 令 =-
则 τ = λ t d = d λ -τ
∞ ∞
∴ f (t) = ∫ f2 (λ) f1(t λ)dλ = f2 (t) f) [ f2 (t) + f3 (t)] = f1(t) f2 (t) + f1(t) f3 (t)
f(t) A 0 a
B
h(t)
Be-αt
0 t
t
(a)
f(t) A 0 a τ A 0
( b)
f(t)
y(t) = ∫ f (τ)h(t τ)dτ
0
t
= ∫ ABe
0
t
α(tτ )
dτ =
AB
α
(1eαt )
(C)
( d)
a t
τ
ⅲ. t≥a ,tl1=0, tl2=-∞,tr1=a, tr2=t
τ
2. 利用卷积积分求电路系统零状态响应的方法: 利用卷积积分求电路系统零状态响应的方法: 方法步骤: 方法步骤: 求出系统的冲击响应h (1)求出系统的冲击响应h(t) 代公式进行卷积积分,或利用卷积性质,求得y (2)代公式进行卷积积分,或利用卷积性质,求得yzs(t) 例1:已知图示电路,(1)输入为 2etU(t) A电流,求响应已知图示电路,( ,(1 电流, iL(t).(2)输入为 2e(t2)U(t 2) A电流,求响应i'L(t) .(2 电流,求响应i' 1.( 求得电路的冲击响应: 解: 1.(1)求得电路的冲击响应: 因为电路KCL: 因为电路KCL: KCL
证明:
d d [ f1(t) f2 (t)] = d t d t
∫
∞
∞
f1( ) f2 (t τ)d τ τ
d 2 (t τ) f = ∫ f1( ) τ d τ ∞ d t d 2 (t) f = f1(t) d t
∞
同理可证第二等式
2.积分 2.积分
∫
证明:
t
∞
[ f1(λ)f2(λ)]dλ = f1(t)∫ f2(λ)dλ
yzs (t) = yzs1(t) + yzs2(t) = (1e )U(t) (1e
t (t ) 1
)U(t 1 )
3.LTIS的完全响应: 利用卷积求得系统零状态响应,再与系统零输入响应叠加, 即求得系统的完全响应为: (设系统特征根互异)
y(t) = yzp(t) + yzs (t) = ∑A e + ∫ f ( )h(t τ)dτ τ zp
yzs (t) = ∫ f (τ)h(t τ)dτ = ∫ f (t τ)h(τ)dτ = f (t)h(t)
t0 t0
t
t
P n (t)
1 τ
h n (t )
LTIS
τ
δ(t) = lim P (t) n
τ → 0
证明:因为任意信号f(t)可以分解为宽度为 τ 的无穷多个窄脉任意信号f 冲信号的迭加
λit
i= 1 0
n
t
4.卷积的图形解法 4.卷积的图形解法 (1). 卷积的图形解释: 卷积实际上是一种数学工具,我们可以用图解法来清楚的说明其含义. h(t)h( τ )
f (t) → f (τ )
tr1 tτ
设:
ta1 -1/2 0 1 (a)
1 0 (b)
τ 2 t
h(τ )
h(t τ )
1
(d)
1 t2 t 3 f (t) h(t) = ∫ 1× (t τ)dτ = + + t2 2 4 2 4
1
(e)
f (t) h(t) = 0
例:求如图(a)(b)所说函数f(t)和h(t)的卷积积分. 解: (1)写出表达式:
A f (t) ={ 0 0 h(t) ={ αt Be
0 <t < a
3.结合律: 3.结合律: 结合律
[ f1(t) f2 (t)] f3 (t) = f1(t) [ f2 (t) f3 (t)]