弹性力学与有限元法分析及实例讲解
- 格式:doc
- 大小:931.50 KB
- 文档页数:14



有限元分析
的一般规律物体在空间的位置随时间的改变
对象内容
任务
对象内容
任务
概述
ANSYS 静力分析z起重机械有限元应用
整机模态分析
车辆安全性
工件淬火3.06 min 时的温度、组织分布(NSHT3D)
同济大学
同济大学
金属反挤压成型:温度分布和变化铸造成型:温度变化和气泡
速度
压力导流管分析
超音速飞行压力分布汽车气动分析
高速导弹气动
同济大学
两根热膨胀系数不同的棒焊接在一起,加热后的变形情况
子结构方法分析大型结构的早期应用法
梁单元
建模时充分利用重复性。


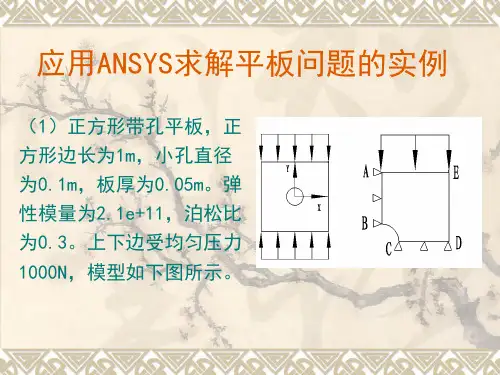
弹性力学与有限元法实验报告学院班级姓名学号实验一一已知条件板孔问题:(其中板厚,,,泊松比),绘出其变形图和在圆心所在的横截面内MISES应力的分布情况。
二实验目的和要求(1)掌握用ANSYS建立开孔平板几何模型的方法。
(2)掌握用ANSYS划分立开孔平板网格的方法。
(3)掌握用ANSYS对开孔平板加载与求解的方法。
(4)掌握用ANSYS对开孔平板计算结果后处理及分析的方法。
三实验过程概述首先做出一个长2000,宽200的长方形,然后在长方形的中央挖出一个直径为10的孔。
将长方形网格化,把固定点设在中心,在两侧分别设一个向外的力P(60KN)。
最后进行运算,结果用云图表示。
四实验内容分析由云图可以看出沿X轴的应力呈线性分布,大小由中间向外递增,其中四个角处的应力也为最小值。
最大应力值在施力点,为0.237406MPa。
形变只发生在施力点处。
由应力图可知,圆心横截面处的应力从外向内递增,但孔处没有应力。
五实验小结和体会对于网格划分,矩形单元比三角形单元更加接近理论求解结果。
而网格加密会使求解结果收敛于理论值,但是这也会加大计算机的计算量。
因此,对于比较复杂的模型,在进行有限元仿真模拟时既要考虑到计算结果的精确度,又要考虑到经济成本的合理性,这时选择一个合理的网格划分就显得十分重要了。
因此,在进行有限元仿真模拟时要选择合适的网格划分方法,划分合理的网格数量。
有限元法是一种求解连续介质、连续场力学和物理问题的数值方法,是工程分析和科学研究的重要工具;必须是对连续地介质等,因而也存在局限性。
实验二一已知条件如图所示支架中的三根杆件材料相同,弹性模量E=200GPa, 泊松比 =0.3,杆1的横截面面积为200mm2,杆2的横截面面积为300mm2,长为1m,杆3的横截面面积为400mm2。
若P=30kN,试求各杆的应力及铰支点的反力。
二实验目的和要求(1)掌握用ANSYS建立杆件系统几何模型的方法。
(2)掌握用ANSYS划分杆件系统网格的方法。




弹性力学及有限元分析1、 设试件两定点之间的长度为L 0,其截面积为F 0,加上拉力P 后,L 0 伸长了△L 。
我们把P/ F 0 称为拉伸应力(σ),△L/ L 0 称为拉伸应变(ε),于是有σ=P/ F 0 ,ε= △L/ L 0某种材料的拉伸应力和拉伸应变的比,称为该材料的杨氏模量或弹性模量(E),即 LF PL E ∆==00εσ,弹性模量E 表征了材料的物理性质。
2、 根据力学特性,固体通常分为韧性固体和脆性固体。
首先分析韧性材料,材料在受力变形过程中,明显地有四个特性点划分三各阶段。
a. 弹性阶段,这一阶段的明显特征是,当外力逐渐去掉时,变形也逐渐消失,物体能够恢复到原来的形状,物体的这种性质称为弹性,存在一个应力极限称为弹性极限。
随着外力的消失而消失的变形称为弹性变形;去掉外力后仍然保留的变形称为残余变形或永久变形。
弹性阶段另一个明显特征是,应力与应变保持线性关系。
设受力方向为x 方向,x xE εσ=,这就是简单拉伸时的虎克定律,弹性模量E 为常数,表示应力与应变成正比例。
通常把弹性极限和比例极限规定为一个值。
b. 塑性阶段,超过弹性极限后,材料开始失去弹性,进入塑性阶段,这时产生较大的永久变形,应力应变关系不再是线性的。
当曲线超过s 点(屈服极限)后,材料开始屈服,即在应力几乎不增加的情况下,应变会不断的增加,称s 点为屈服极限;当变形大到一定程度后,材料开始强化,要继续增加变形必须再增加外力,到达b 点后产生颈缩。
从弹性极限到b 的变形范围统称为塑性阶段,属于塑性力学的研究范畴。
c. 断裂阶段,试件产生颈缩后,开始失去抵抗外力的能力,最后发生断裂,相对于b点的应力称为强度极限。
脆性材料:它的拉伸曲线图没有明显的三个阶段之分,也没有明显的屈服应力点,材料亦不再满足虎克定律。
为了分析上的需要,往往以切线斜率作为弹性模量,即εσd d E =。
如果对脆性固体材料加载,应力应变曲线将沿着OA 上升,若到A 点后即行卸载,应力应变曲线并不沿着原来的途径回复到原点,而是沿着直线AB 下降,当全部载荷卸去之后,试件中尚残存一部分永久变形''ε。

弹性力学与有限元法分析
弹性力学是固体力学的一个重要分支,是研究弹性固体在受外力作用、温度改变、边界约束或其他外界因素作用下而发生的应力、形变和位移状态的科学。
有限单元法是力学、数学、物理学、计算方法、计算机技术等多种学科综合发展和结合的产物,是随着计算机技术的广泛应用而迅速发展起来的一种数值分析方法。
有限元法的基本思想就是化整为零,分散分析,再集零为整。
即用结构力学方法求解弹性力学问题,实质是将复杂的连续体划分为有限多个简单的单元体,单元体之间仅仅通过结点相连,实现化无限自由度问题为有限稀有度问题,将连续场函数的(偏)微分方程的求解问题转化为有限个参数的代数方程组的求解问题。
有限元方法经过近半个世纪的发展,目前已经成为各种工程问题特别是结构分析问题的标准分析方法,而有限元软件也已成为现代结构设计中不可缺少的工具。
有限元软件是有限元理论通向实际工程应用的桥梁,它的应用极大地提高了力学学科解决自然科学和工程实际问题的能力,进一步促进了有限元方法的发展。
ANSYS软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件,广泛用于机械制造、石油化工、航空航天、汽车交通、土木工程、造船、水利等一般工业及科学研究。
ANSYS软件的组成:
(一)前处理模块
该模块为用户提供了一个强大的实体建模及网格划分工具,可以方便的构造有限元模型,软件提高了100种以上的单元类型,用来模拟工程中的各种结构和材料。
包括:
1.实体建模:参数化建模,布尔运算及体素库,拖拉、旋转、拷贝、蒙皮、倒角等。
2.自动网格划分,自动进行单元形态、求解精度检查及修正。
3.在集合模型上加载:点加载、分布载荷、体载荷、函数载荷。
4.可扩展的标准梁截面形状库。
(二)分析计算模块
该模块包括结构分析(可进行线性分析、非线性分析和高度非线性分析)、流体动力学分析、电磁场分析、声场分析、压电分析以及多物理场的耦合分析,可模拟多种物理介质的相互作用,具有灵敏度分析及优化分析能力。
(三)后处理模块
将计算结果以彩色等值线、梯度、矢量、粒子流、立体切片、透明及半透明等图形方式显示出来,也可以用图表、曲线形式显示或输出。
由于现在只是对ANSYS工程软件有初步的了解和掌握,所以本次作业仅以(1)结构静力学分析为例,运用ANSYS软件对汽车连杆进行受力分析;(2)
三杆桁架的优化设计为例。
举例1:对连杆进行受力分析
结构静力学分析是ANSYS工程软件中应用最广泛的一种分析方法,“结构”不仅包含像桥梁、建筑物等建筑工程结构,也包括像活塞、机械零件和工具等机械零部件一样的船只、航空和机械结构,如船的外壳、航空器、机器的机架等。
结构静力学分析用来求解稳态外载荷引起的系统或部件的位移、应变、应力和力,稳态载荷包括外部施加的力和压力、稳态的惯性力(重力和旋转速度、施加位移、温度等)。
静力分析很适合求解惯性和阻尼对结构的影响并不显著的问题,如确定结构中的应力集中现象,可以进行线性分析,也可以进行非线性分析,如塑性、蠕变、膨胀、大应变及接触分析。
静力分析过程分为三个步骤:
图1. 静力分析过程三步骤
如图所示为汽车连杆的几何模型,连杆的厚度为0.5in,图中所注尺寸均为英寸,在小头孔的内侧90度范围内承受p=1000psi的面载荷作用,试利用有限元分析该连杆的受力状态。
连杆的材料属性为:杨氏模量E=30×106psi,泊松比为0.3。
连杆的几何模型
1.建立计算模型
本例是对一个弹性力学平面问题进行结构分析,所以只选择结构分析模块。
由于连杆的结构、载荷均对称,因此在分析时只要采用一半进行分析即可。
采用由底向上的建模方式,具体的操作过程如下:
(1)生成圆环面和两个矩形,包括创建关键点、直线、样条曲线、倒圆角等;通过对面进行布尔操作产生真实模型。
图1.1 生成连杆大头圆环面、矩形
图1.2 生成连杆小头圆环面,进行布尔运算
图1.3 创建样条曲线
图1.4 生成连杆轮廓线
图1.5 由边界线生成面
(2)划分网格,包括定义单元类型:选择单元为solid,quad 8–node,设置
单元尺寸为0.2,采取自由网格划分用20节点的SOLID95单元划分网格。
图1.6 采用自由划分网格,生成2D网格
图1.7 生成3D网格
(3)定义材料属性
对平面连杆进行线弹性分析计算,所定义的材料属性有弹性模量E=30×106psi,泊松比为0.3。
2. 施加约束和载荷并求解
(1)施加约束
图2.1 大孔内表面施加对称约束
(2)施加载荷
2.3 小孔内表面施加面载荷
(3)选择PCG求解器,求解运算
3.查看显示结果
图4 连杆体的受力分布显示
由受力图可知,当连杆小头内侧受到面分布载荷时,小头孔内侧靠近大头孔部分受力最大,在一定的条件下,可能最先出现裂纹,也最容易断裂。
举例2:三杆桁架的优化设计
优化设计是一种寻找确定最优设计方案的技术,人们总希望在一切可能的方
案中选择一个最好的,设计方案的任何方面都可以优化,进行优化设计首先要把实际的实际问题用数学表达式加以描述,转化成数学模型,然后根据数学模型的特性,选择某种适当的优化计算方法及其程序,通过计算机求得最优解。
优化设计的步骤:
(1)生成循环所用的分析文件,建立优化过程中的参数;
(2)进入OPT处理器,指定分析文件,指定优化变量;
(3)选择优化工具或优化方法;指定优化循环控制方式;
(4)进行优化分析;
(5)查看设计序列结果。
如图所示为一个由三根杆组成的桁架结构,它承受纵向和横向载荷,求该桁架的最小质量。
图1. 桁架结构模型
已知桁架特性如下表所示:
表1
标函数如下:
()()⎪⎪
⎪⎩
⎪
⎪
⎪
⎨⎧
=≤≤≤≤=≤⨯==-321j pa 76.2max 025101,2,3i 0.64516A 106.0t .s B],A ,A ,A []x ,x ,x ,[x X f Min j i 3
3214321,,M B σχ 1.1 参数化建立几何模型
(1)定义参数和材料属性
参数初始值:B=25,A1=A2=A3=0.645;材料属性:E=2e11,PRXY=0.3,DENS=7800 (2)定义单元类型及属性
单元类型:structural link –2D spar 1;定义实常数:A1,A2,A3。
(3)建立有限元模型
图1.1 生成单元
(4)施加约束和载荷
图1.2 施加边界约束
图1.3 4节点施加集中载荷
1.2 求解运算
2.1 提取并指定状态变量和目标函数
计算单元体积的总和VTOT=61.7333874;计算初始重量:WT=481520.422
显示单元形状和大小:
图1.4 单元形状和大小
2.2 进入优化处理器,指定分析文件
指定分析文件为:hangjia_opt.lgw,指定设计变量:A1、A2、A3、B;设置状态变量:sig1、sig2、sig3;设置目标函数:WT,允差为1;指定一阶优化方法:first–order。
3.1查看优化结果
信息窗口中将显示了迭代序列的结果,包括每个设计变量、状态变量、目标函数的值。
所有序列的结果见程序文件。
3.2显示目标函数的变化规律
3.3 显示基本尺寸的变化规律
图3.3 B的变化规律
3.4 显示杆横截面的变化规律
的变化规律
图3.4 A
i
3.5 显示杆中应力的变化规律
的变化规律
图3.5
j。