2 2014·高一·期末·格致中学数学

2014-2015学年上海市黄浦区格致中学高一（上）期中数学试卷一、填空题：（每小题4分，满分40分）1．（4分）函数f（x）=的定义域为．2．（4分）设集合M={0，1，2}，N={x|x2﹣3x+2≤0}，则M∩N=．3．（4分）不等式组的解集为．4．（4分）已知集合A={1，4，x}，B={1，x2}，其中x∈N．且A∪B=A，则x=．5．已知全集U=N，集合A={1，4，x}，集合B={1，x2}，若∁U A⊊∁U B，则x=．6．（4分）已知函数f（x）为奇函数，且当x＜0时，f（x）=x2﹣，则f（1）=．7．已知函数f（x）是定义在R上的奇函数，g（x）=f（x）+ax3+2，若g（2）=6，则g（﹣2）=．8．（4分）平面直角坐标系中，若点在第三象限内，则实数a 的取值范围是．9．（4分）已知集合M={x|x2+x﹣6=0}，N={y|ay+2=0，a∈R}，若满足M∩N=N 的所有实数a形成集合为A，则A的子集有个．10．定义|b﹣a|为区间（a，b）（a，b∈R，a＜b）的长度．则不等式的所有解集区间的长度和为．11．（4分）若不等式x2+ax+b＜0的解集为（﹣3，﹣1），则不等式bx2+ax+1≤0的解集为．12．（4分）若a、b为正实数，且a+b+3=ab，则ab的最小值为．13．已知正数x、y满足：2x+y﹣xy=0，则x+2y的最小值为．14．（4分）若集合{a，b，c，d}={1，2，3，4}，且下列四个关系：①a=1；②b≠1；③c=2；④d≠4有且只有一个是正确的，则符合条件的有序数组（a，b，c，d）的个数是．二、选择题：（每小题4分，满分16分）15．（4分）若集合，集合B={x||x|≤5，x∈Z}，则集合A∪B中的元素个数为（）A．11 B．13 C．15 D．1716．（4分）设函数f（x）与g（x）分别是定义在R上的奇函数与偶函数，函数f（x）的零点个数为F，g（x）的零点个数为G，且F、G都是常数．则下列判断正确的是（）A．F一定是奇数，G可能是奇数B．F可能是偶数，G一定是偶数C．F一定是奇数，G一定是偶数D．F可能是偶数，G可能是奇数17．（4分）设全集为U，对于集合A，B，则“A∩B≡∅”是“存在集合C，使得A⊊C且B⊊∁U C”的（）A．充分不必要条件 B．必要不充分条件C．充分必要条件D．既不充分又不必要条件18．已知函数f（x）定义域为D，区间（m，n）⊆D，对于任意的x1，x2∈（m，n）且x1≠x2，则“f（x）是（m，n）上的增函数”是“”的（）A．充分不必要条件 B．充分必要条件C．必要不充分条件 D．既不充分又不必要条件19．（4分）给出下列说法：（1）命题“若a、b都是奇数，则a+b是偶数”的否命题是“若a、b都不是奇数，则a+b不是偶数”；（2）命题“如果A∩B=A，那么A∪B=B”是真命题；（3）“x≠1或y≠2”是“x+y≠3”的必要不充分条件．那么其中正确的说法有（）A．0个 B．1个 C．2个 D．3个三、解答题：（共5大题，满分44分）20．（6分）已知集合A={x||x﹣2|＜a}，集合，且A⊆B，求实数a的取值范围．21．（8分）一次函数f（x）是R上的增函数，g（x）=f（x）（x+m），已知f[f（x）]=16x+5．（1）求f（x）（2）当x∈[1，3]时，g（x）有最大值13，求实数m的值．22．（10分）设函数f（x）=2|x﹣1|+x﹣1，g（x）=16x2﹣8x+1．记f（x）≤1的解集为M，g（x）≤4的解集为N．（Ⅰ）求M；（Ⅱ）当x∈M∩N时，证明：x2f（x）+x[f（x）]2≤．23．（10分）已知函数f（x）=x2﹣2ax﹣2（a+1）（a∈R）．（1）求证：函数f（x）的图象与x轴恒有两个不同的交点A、B，并求此两交点之间距离的最小值；（2）若f（x）+3≥0在区间（﹣1，+∞）上恒成立，求实数a的取值范围．24．（10分）已知函数f（x）=lg（x2﹣mx﹣m）．（1）若m=1，求函数f（x）的定义域；（2）若f（x）在（1，+∞）上是增函数，求实数m的取值范围．2014-2015学年上海市黄浦区格致中学高一（上）期中数学试卷参考答案与试题解析一、填空题：（每小题4分，满分40分）1．（4分）函数f（x）=的定义域为（﹣1，+∞）．【解答】解：要使函数有意义，则x+1＞0，即x＞﹣1，故函数的定义域为（﹣1，+∞），故答案为：（﹣1，+∞）2．（4分）设集合M={0，1，2}，N={x|x2﹣3x+2≤0}，则M∩N={1，2} ．【解答】解：由N中不等式变形得：（x﹣1）（x﹣2）≤0，解得：1≤x≤2，即N=[1，2]，∵M={0，1，2}，∴M∩N={1，2}，故答案为：{1，2}3．（4分）不等式组的解集为（0，1）．【解答】解：由得，，解得0＜x＜1，所以不等式的解集是（0，1），故答案为：（0，1）．4．（4分）已知集合A={1，4，x}，B={1，x2}，其中x∈N．且A∪B=A，则x=0．【解答】解：∵集合A={1，4，x}，B={1，x2}，其中x∈N．A∪B=A，∴B⊂A，∴，解得x=0．故答案为：0．5．已知全集U=N，集合A={1，4，x}，集合B={1，x2}，若∁U A⊊∁U B，则x=0或2．【解答】解：全集U=N，集合A={1，4，x}，集合B={1，x}，若∁U A⊊∁U B，可得B⊊A，即有x2=4或x2=x，解得x=±2或0或1，检验x=﹣2舍去，x=1也不成立．则x=0，2成立．故答案为：0或2．6．（4分）已知函数f（x）为奇函数，且当x＜0时，f（x）=x2﹣，则f（1）=﹣2．【解答】解：∵函数f（x）是奇函数，∴f（﹣1）=﹣f（1），∵当x＜0时，f（x）=x2﹣，∴f（1）=﹣f（﹣1）=﹣（1+1）=﹣2．故答案为﹣2．7．已知函数f（x）是定义在R上的奇函数，g（x）=f（x）+ax3+2，若g（2）=6，则g（﹣2）=﹣2．【解答】解：∵函数f（x）是定义在R上的奇函数，g（x）=f（x）+ax3+2，若g（2）=f（2）+8a+2=6，则f（2）+8a=4．∴g（﹣2）=f（﹣2）﹣8a+2=﹣f（2）﹣8a+2=﹣4+2=﹣2，故答案为：﹣2．8．（4分）平面直角坐标系中，若点在第三象限内，则实数a的取值范围是．【解答】解：∵点在第三象限内，∴，则，解得，∴实数a的取值范围是，故答案为：．9．（4分）已知集合M={x|x2+x﹣6=0}，N={y|ay+2=0，a∈R}，若满足M∩N=N 的所有实数a形成集合为A，则A的子集有个8．【解答】解：∵集合M={x|x2+x﹣6=0}={﹣3，2}，N={y|ay+2=0，a∈R}={﹣}，∵M∩N=N，∴N⊂M，∴﹣不存在，或﹣=﹣3，或﹣，解得a=0或a=或a=﹣1，∴集合A={﹣1，0，}，∴A的子集有23=8个．故答案为：8．10．定义|b﹣a|为区间（a，b）（a，b∈R，a＜b）的长度．则不等式的所有解集区间的长度和为8．【解答】解：由得，化简得，即，等价于（x﹣2）（x﹣8）x（x+2）＜0，如图所示：由图可得，不等式的解集是（﹣2，0）∪（2，8），∴不等式所有解集区间的长度和是2+6=8，故答案为：8．11．（4分）若不等式x2+ax+b＜0的解集为（﹣3，﹣1），则不等式bx2+ax+1≤0的解集为[﹣1，﹣] ．【解答】解：不等式x2+ax+b＜0的解集为（﹣3，﹣1），∴方程x2+ax+b=0的两个实数根为﹣3和﹣1，由根与系数的关系得：a=4，b=3，故bx2+ax+1≤0可化为：3x2+4x+1≤0，解得﹣1≤x≤﹣；所求不等式bx2+ax+1≤0的解集为[﹣1，﹣]．故答案为：[﹣1，﹣]．12．（4分）若a、b为正实数，且a+b+3=ab，则ab的最小值为9．【解答】解：∵a、b为正实数，∴a+b+3=ab≥+3，化为：≥0，解得≥3，即ab≥9．当且仅当a=b=3时取等号．则ab的最小值为9．故答案为：9．13．已知正数x、y满足：2x+y﹣xy=0，则x+2y的最小值为9．【解答】解：∵正数x、y满足：2x+y﹣xy=0，∴=1．则x+2y=（x+2y）=5++≥5+2×=9，当且仅当x=y=3时取等号．因此x+2y的最小值为9．故答案为：9．14．（4分）若集合{a，b，c，d}={1，2，3，4}，且下列四个关系：①a=1；②b≠1；③c=2；④d≠4有且只有一个是正确的，则符合条件的有序数组（a，b，c，d）的个数是6．【解答】解：由题意，a=2时，b=1，c=4，d=3；b=3，c=1，d=4；a=3时，b=1，c=4，d=2；b=1，c=2，d=4；b=2，c=1，d=4；a=4时，b=1，c=3，d=2；∴符合条件的有序数组（a，b，c，d）的个数是6个．二、选择题：（每小题4分，满分16分）15．（4分）若集合，集合B={x||x|≤5，x∈Z}，则集合A∪B中的元素个数为（）A．11 B．13 C．15 D．17【解答】解：∵集合={x|，x∈N}={4，5，6，7，8，9}，集合B={x||x|≤5，x∈Z}={x|﹣5≤x≤5，x∈Z}={﹣5，﹣4，﹣3，﹣2，﹣1，0，1，2，3，4，5}，∴A∪B={﹣5，﹣4，﹣3，﹣2，﹣1，0，1，2，3，4，5，6，7，8，9}．∴集合A∪B中的元素个数为15．故选：C．16．（4分）设函数f（x）与g（x）分别是定义在R上的奇函数与偶函数，函数f（x）的零点个数为F，g（x）的零点个数为G，且F、G都是常数．则下列判断正确的是（）A．F一定是奇数，G可能是奇数B．F可能是偶数，G一定是偶数C．F一定是奇数，G一定是偶数D．F可能是偶数，G可能是奇数【解答】解：函数f（x）是定义在R上的奇函数，可得f（0）=0，奇函数的图象关于原点对称，所以函数的零点个数一定是奇数个．g（x）是定义在R上的偶函数．函数的图象关于y轴对称，g（0）可能为0，所以函数的零点个数可能为奇数个．故选：A．17．（4分）设全集为U，对于集合A，B，则“A∩B≡∅”是“存在集合C，使得A⊊C且B⊊∁U C”的（）A．充分不必要条件 B．必要不充分条件C．充分必要条件D．既不充分又不必要条件【解答】解：“存在集合C，使得A⊊C且B⊊∁U C”⇒“A∩B=∅”，反之也成立．因此“A∩B≡∅”是“存在集合C，使得A⊊C且B⊊∁U C”的充要条件．故选：C．18．已知函数f（x）定义域为D，区间（m，n）⊆D，对于任意的x1，x2∈（m，n）且x1≠x2，则“f（x）是（m，n）上的增函数”是“”的（）A．充分不必要条件 B．充分必要条件C．必要不充分条件 D．既不充分又不必要条件【解答】解：“”⇔（x1﹣x2）[f（x1）﹣f（x2）]＞0，⇔x1﹣x2与f（x1）﹣f（x2）同号．∴对于任意的x1，x2∈（m，n）且x1≠x2，则“f（x）是（m，n）上的增函数”是“”的充要条件．故选：B．19．（4分）给出下列说法：（1）命题“若a、b都是奇数，则a+b是偶数”的否命题是“若a、b都不是奇数，则a+b不是偶数”；（2）命题“如果A∩B=A，那么A∪B=B”是真命题；（3）“x≠1或y≠2”是“x+y≠3”的必要不充分条件．那么其中正确的说法有（）A．0个 B．1个 C．2个 D．3个【解答】解：对于（1）命题“若a、b都是奇数，则a+b是偶数”的否命题是“若a、b都不是奇数，则a+b不是偶数”；不满足否命题的形式，应该为：若a、b不都是奇数，则a+b不是偶数．所以（1）不正确；对于（2）命题“如果A∩B=A，那么A∪B=B”是真命题；满足集合的交集与并集的关系，正确；对于（3）“x≠1或y≠2”是“x+y≠3”的必要不充分条件．根据逆否命题的等价性可知，条件可转化为x+y=3是x=1且y=2的条件关系，当x=1且y=2，有x+y=3成立．但x+y=3时，比如x=2，y=1时，满足x+y=3，但此时x=1且y=2不成立．∴x+y=3是x=1且y=2成立的必要不充分条件．即“x≠1或y≠2”是“x+y≠3”的必要不充分条件．正确．故选：C．三、解答题：（共5大题，满分44分）20．（6分）已知集合A={x||x﹣2|＜a}，集合，且A⊆B，求实数a的取值范围．【解答】解：由≤1，化为：≤0，解得﹣2≤x≤3，即B=[﹣2，3]．a≤0时，A=∅，满足A⊆B，因此a≤0适合题意．a＞0时，A=[2﹣a，2+a]，A⊆B，∴﹣2≤2﹣a，2+a≤3，a＞0，解得0＜a≤1．综上可得：实数a的取值范围是（﹣∞，1]．21．（8分）一次函数f（x）是R上的增函数，g（x）=f（x）（x+m），已知f[f（x）]=16x+5．（1）求f（x）（2）当x∈[1，3]时，g（x）有最大值13，求实数m的值．【解答】解：（1）一次函数f（x）是R上的增函数，可设f（x）=ax+b，（a＞0）；∴f[f（x）]=a（ax+b）+b=a2x+ab+b=16x+5，∴，解得或（不合题意舍去）；∴f（x）=4x+1；（2）g（x）=f（x）（x+m）=（4x+1）（x+m）=4x2+（4m+1）x+m，是二次函数，开口向上，且对称轴为x=﹣，①当﹣≤1，即m≥﹣时，g（x）在[1，3]上是单调增函数，令g（x）max=g（3）=39+13m=13，解得m=﹣2，符合题意；②当﹣＞1，即m＜﹣时，g（x）max=g（1）=5+5m=13，解得m=，不符合题意；由①②可得m=﹣2．22．（10分）设函数f（x）=2|x﹣1|+x﹣1，g（x）=16x2﹣8x+1．记f（x）≤1的解集为M，g（x）≤4的解集为N．（Ⅰ）求M；（Ⅱ）当x∈M∩N时，证明：x2f（x）+x[f（x）]2≤．【解答】解：（Ⅰ）由f（x）=2|x﹣1|+x﹣1≤1 可得①，或②．解①求得1≤x≤，解②求得0≤x＜1．综上，原不等式的解集为[0，]．（Ⅱ）证明：由g（x）=16x2﹣8x+1≤4，求得﹣≤x≤，∴N=[﹣，]，∴M∩N=[0，]．∵当x∈M∩N时，f（x）=1﹣x，∴x2f（x）+x[f（x）]2 =xf（x）[x+f（x）]=﹣≤，故要证的不等式成立．23．（10分）已知函数f（x）=x2﹣2ax﹣2（a+1）（a∈R）．（1）求证：函数f（x）的图象与x轴恒有两个不同的交点A、B，并求此两交点之间距离的最小值；（2）若f（x）+3≥0在区间（﹣1，+∞）上恒成立，求实数a的取值范围．【解答】（1）证明：∵f（x）=x2﹣2ax﹣2（a+1）（a∈R），∴△=4a2﹣4×（﹣2）（a+1）=4（a+1）2+4＞0恒成立，∴函数f（x）的图象与x轴恒有两个不同的交点A、B，设A（x1，0），B（x2，0），则x1+x2=2a，x1x2=﹣2（a+1），则|AB|2=（x1+x2）2﹣4x1x2=4（a+1）2+4≥4（当且仅当a=﹣1时取等号），∴|AB|min=2．（2）解：若f（x）+3≥0在区间（﹣1，+∞）上恒成立，则x2﹣2ax﹣2（a+1）+3=x2﹣2ax﹣2a+1≥0（x＞﹣1）恒成立，分离参数a得：2a（x+1）≤x2+1（x＞﹣1）恒成立，∵x＞﹣1，∴x+1＞0，∴2a≤（）min，∵=x+1+﹣2≥2﹣2=2﹣2，∴（）min=2﹣2，∴a≤﹣1．24．（10分）已知函数f（x）=lg（x2﹣mx﹣m）．（1）若m=1，求函数f（x）的定义域；（2）若f（x）在（1，+∞）上是增函数，求实数m的取值范围．【解答】解：（1）当m=1时，f（x）=lg（x2﹣x﹣1），必有x2﹣x﹣1＞0，解可得x＞或x＜，则函数f（x）=lg（x2﹣x﹣1）的定义域为{x|x＞或x＜}；（2）根据题意，若f（x）在（1，+∞）上是增函数，则必有，解可得m≤2，则实数m的取值范围为{m|m≤2}．赠送初中数学几何模型【模型五】垂直弦模型：图形特征：运用举例：1.已知A、B、C、D是⊙O上的四个点.(1)如图1，若∠ADC＝∠BCD＝90°，AD＝CD，求证AC⊥BD；(2)如图2，若AC⊥BD，垂足为E，AB＝2，DC＝4，求⊙O的半径.2.如图，已知四边形ABCD 内接于⊙O ，对角线AC ⊥BD 于P ，设⊙O 的半径是2。

格致中学高一期末数学试卷2021.01一.填空题1.已知集合A={-3,-2,-1,0,1,2,3}, B={x||x -1|≤1},则A∩B=_____.2.函数2log (1)()2x f x x -=-的定义域为_____. 3.若指数函数y=f(x)的图像经过点1(,2),2则函数1()2x y f x +=-的零点为_____. 4.不等式1||x x <的解集为_____. 5.已知6log 2,a =用a 表示4log 12=_____.6.已知函数2(log )x y a =在R 上是严格减函数,则实数a 的取值范围是_____.7.定义区间[a,b](a<b)的长度为b -a,若关于x 的不等式.240x x m -+≤的解集区间长度为2,则实数m 的值为_____.8.设,(1,),x y ∈+∞22log ,log x y 的算术平均值为1,则22x y ，的几何平均值的最小值为_____.9.已知函数y=f(x)是R 上的奇函数,且是(-∞,0)上的严格减函数,若f(1)=0,则满足不等式(x -1)f(x)≥0的x 的取值范围为_____.10.已知124{2,1,,,,2},333a ∈--当x ∈(-1,0)∪(0,1)时,不等式||a x x >恒成立,则满足条件的a 形成的集合为_____.11.函数y=f(x)(x<0)的反函数为1(),y f x -=且函数2()0()log (1)0f x x g x x x <⎧=⎨+≥⎩是奇函数,则不等式1()2f x -≥-的解集为_____.12.已知函数()|21|,x f x =-若函数21()()()4g x f x mf x =++有4个零点,则实数m 的取值范围为_____. 二.选择题13.已知陈述句α是β的必要非充分条件,集合M={x|x 满足α},集合N={x|x 满足β},则M 与N 之间的关系为()A.M ⊂NB.M ⊃NC.M=ND.M N ⋂=∅ 14.若33log log m n <且log 3log 3m n <，则实数m 、n 满足的关系式为()A.0<m<n<1B.0<n<m<1C.0<m<1<nD.1<m<n15.设121221,,,,,b a b c c a 都是非零实数,不等式21110a x b x c ++>的解集为A,不等式22220a x b x c ++>的解集为B,则"A=B"是“1112220a b c a b c ==>”的() A.充分非必要条件B.必要非充分条件C.充分必要条件D.既非充分又非必要条件16.定义在R 上的函数y=f(x)的表达式为2(),x x f x x x ⎧∈⎪=⎨∈⎪⎩Q Q 给出下列3个判断:(1)函数y=f(x)是非奇非偶函数;(2)当a<0且a ∈Q 时,方程f(x)=a 无解;(3)当a>0时,方程f(x)=a 至少有一解;其中正确的判断有()A.0个B.1个C.2个D.3个三.解答题17.已知集合A={x||x -a|≤2},不等式2112x x -≥+的解集为B. (1)用区间表示B;(2)若全集U=R ,且,A B A ⋂=求实数a 的取值范围.18.已知a ､b 都是正实数,且.b b a a=- (1)求证:a>1;(2)求b 的最小值.19.设函数y=f(x)的表达式为2()||,f x x x a =+-其中a 为实常数.(1)判断函数y=f(x)的奇偶性,并说明理由;(2)设a>0,函数()()f xg xx在区间(0,a]上为严格减函数,求实数a的最大值.20.已知非空集合S的元素都是整数,且满足:对于任意给定的x,y∈S (x､y可以相同),有x+y∈S且x-y∈S.(1)集合S能否为有限集,若能,求出所有有限集,若不能,请说明理由;(2)证明:若3∈S且5∈S,则S=Z.。

上海市东格致中学高一数学文上学期期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 有60瓶矿泉水，编号为1至60，若从中抽取6瓶检验，则用系统抽样确定所抽的编号为()A．3，13，23，33，43，53B．2，14，26，38，42，56C．5，8，31，36，48，54 D．5，10，15，20，25，30参考答案：A略2. 已知是等差数列，，，则此数列的通项公式是A. B. C. D.参考答案：C略3. 已知向量，若与垂直，则A B CD 4参考答案：C4. 已知平面上不重合的四点P，A，B，C满足++=且++m=，那么实数m的值为（）A．2 B．﹣3 C．4 D．5参考答案：B【考点】平面向量的基本定理及其意义．【分析】利用向量基本定理结合向量的减法有： =﹣， =﹣，代入化简即得【解答】解：由题意得，向量的减法有： =﹣， =﹣．∵++m=，即+=﹣m，∴+﹣=﹣m=m，∴ +=（m+2）．∵++=，∴ +（m+2）=0，∴m=﹣3，故选：B．【点评】本小题主要考查平面向量的基本定理及其意义、向量数乘的运算及其几何意义等基础知识．本题的计算中，只需将向量都化成以P为起点就可以比较得出解答了，解答的关键是向量基本定理的理解与应用，属于中档题．5. （5分）若sin（+θ）=，则cos（π﹣θ）等于（）A．﹣B．C．﹣D．参考答案：A考点：运用诱导公式化简求值．专题：计算题；三角函数的求值．分析：由已知及诱导公式可求得cosθ的值，从而化简可求后代入即可求值．解答：解：sin（+θ）=cosθ=，则cos（π﹣θ）=﹣cosθ=﹣，故选：A．点评：本题主要考察了诱导公式的应用，属于基础题．6. 在中，点是延长线上一点，若，则（）A. B. C. D.参考答案：C7. 在中，，，则k的值为（）A．5 B．C．D．参考答案：D∵，∴，得，∴选“D”．8. （5分）①正相关，②负相关，③不相关，则下列散点图分别反映的变量是（）A．①②③B．②③①C．②①③D．①③②参考答案：D考点：散点图．专题：计算题；概率与统计．分析：由图分析得到正负相关即可．解答：第一个图大体趋势从左向右上升，故正相关，第二个图不相关，第三个图大体趋势从左向右下降，故负相关，故选D．点评：本题考查了变量相关关系的判断，属于基础题．9. 不等式的解集为（）A、B、C、D、参考答案：D10. 在△ABC中， =， =，且?＞0，则△ABC是（）A．锐角三角形B．直角三角形C．等腰直角三角形D．钝角三角形参考答案：D【考点】GZ：三角形的形状判断．【分析】根据已知推断出?＜0，进而根据向量的数量积的运算推断出B＞90°．【解答】解：∵?＞0∴?＜0∴B＞90°，即三角形为钝角三角形，故选：D．二、填空题:本大题共7小题,每小题4分,共28分11. 设函数，则____________．参考答案：912. 用一张圆弧长等于 分米，半径是10分米的扇形胶片制作一个圆锥体模型，这个圆锥体的体积等于_ __立方分米． 参考答案： 96π 略13. 函数的单调递增区间是 .参考答案：[-1，1）略14. 关于的不等式（）的解集为 ．参考答案：略15. 已知函数f （x ）=log 2（4x+1）+mx ，当m ＞0时，关于x 的不等式f （log 3x ）＜1的解集为 ．参考答案：（0,1） 函数 ，当时，可知f(x)单调递增函数，当 时，可得，那么不等式 的解集，即，解得，故答案为.16. 在△ABC 中，，，,则△ABC 的面积S 是___________．参考答案：.【分析】 根据三角形的面积公式即可求解．【详解】由三角形的面积公式可知故答案为：．【点睛】本题主要考查三角形中面积公式的应用，属于简单题．17. 已知，则的值为________________.参考答案：略三、 解答题：本大题共5小题，共72分。

2024届上海市黄浦区格致中学数学高一下期末质量跟踪监视试题请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本大题共10小题，每小题5分，共50分。

在每个小题给出的四个选项中，恰有一项是符合题目要求的1．已知,R λμ∈，ABC ∆所在平面内一点P 满足AB BC AC CB AP AB AC AB BC AC CB λμ⎛⎫⎛⎫ ⎪ ⎪=++=++ ⎪ ⎪⎝⎭⎝⎭，则BPCP =（ ）A ．sin 2sin 2BC B ．cos 2cos 2B C C ．sin2sin2C BD ．cos 2cos 2CB2．若实数,x y 满足26403xy x x ⎛⎫+=<< ⎪⎝⎭，则41x y +的最小值为( ) A ．4B ．8C ．16D ．323．某市家庭煤气的使用量3(m )x 和煤气费()f x (元) 满足关系,0()(),C x Af x C B x A x A<≤⎧=⎨+->⎩，已知某家庭今年前三个月的煤气费如下表：若四月份该家庭使用了320m 的煤气，则其煤气费为（ ）元 A ．10.5B ．10C ．11.5D ．114．已知等差数列{a n },若a 2=10,a 5=1,则{a n }的前7项和为 A ．112 B ．51C ．28D ．185．设13cos 6sin 6,22a =+22tan171cos70,1tan 17b c -==+，则有( )A ．b c a <<B ．c b a <<C ．c a b <<D ．a c b <<6．在中，已知，，则角的取值范围为（ ） A ． B ． C ．D ．7．sin 210︒的值为（ ） A ．12B ．12-C ．32D ．32-8．已知向量(3,1)a =-，(3,1)b =，则a 在b 方向上的投影为（） A ．15B ．14C ．13D ．19．关于x 的不等式()210x a x a -++<的解集中，恰有3个整数，则a 的取值范围是（ ）A ．[)(]3,24,5--⋃B ．()()3,24,5--⋃C ．(]4,5D ．（4,5）10．若()cos sin f x x x =-在[],a a -是减函数，则a 的最大值是A ．4πB ．2π C ．34π D ．π二、填空题：本大题共6小题，每小题5分，共30分。

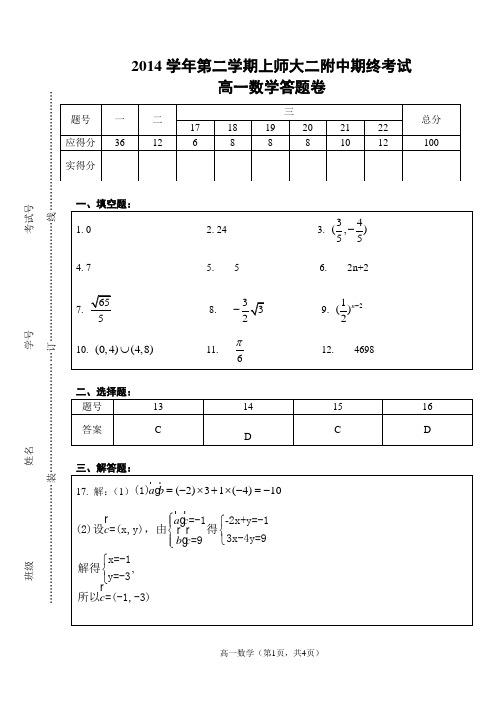
2014学年第二学期上师大二附中期终考试高一数学答题卷一、填空题：1. 02. 243. 34(,)55-4. 75. 56. 2n+27.6558. 332- 9. 21()2n - 10. (0,4)(4,8)⋃ 11. 6π12. 4698二、选择题： 题号 13 14 15 16 答案 CDCD三、解答题：17. 解：（1）(2)31(4)10a b =-⨯+⨯-=-(1)-,a c c b c c ⎧⎧⎪⎨⎨⎩⎪⎩⎧⎨⎩=-12x+y=-1(2)设=(x,y)，由得3x-4y=9=9x=-1解得y=-3所以=(-1,-3)题号 一 二 三总分 17 18 19 20 21 22 应得分 36 12 6 8 8 8 10 12 100 实得分班级__________________ 姓名__________________ 学号__________________ 考试号__________________………………………………装………………………………订………………………………线………………………………18. 解：（1）设等差数列{}n a 的公差为d .因为36a =-,60a =， 所以112650a d a d +=-⎧⎨+=⎩，解得110a =-,2d =. …………………………2分??所以*10(1)2212,n a n n n N =-+-⨯=-∈. …………………………4分 （2）设等比数列{}n b 的公比为q .因为2123124,8b a a a b =++=-=-， 所以824,3q q -=-=. ……………………………………………………6分 所以数列{}n b 的前n 项和公式为*1(1)4(13),1n n n b q S n N q-==-∈-．……………………………………8分19. 解：（1）1211333213732a a a ⋅===++ ……………………………………1分 2323333733837a a a ⋅===++ ………………………………………2分3433331833338a a a ⋅===++ (3)（2）猜测：35n a n =+ ………………………………………………4分证明：①当1n =时，显然成立 ……………………………………5分②假设n k =时猜测成立，即35k a k =+则当1n k =+时，()133335331535k k k a k a a k k +⋅+===+++++ …………………7分 ∴猜测也成立 由①②得：35n a n =+对一切n *∈N 都成立 (8)请在黑色矩形边框内答题，超出黑色矩形边框的答题一律无效20. =,(1,2)//3(2)1(1),(2)(14,7),=-OC OC OB OC OB BC OC OB x y BC OA y x OC OD OA OC OD OC OA ⊥∴=-=+-∴-=+⎧∴=⎨⎩+=∴解：设（x,y ）,=-x+2y=0,(1)，x=14由（1）（2）得，y=7又，=（11,6）21. 解：（1）证明：1111211111()3213[()]21212n n n n n n n n n nn na a a a a ab b a a ++++++++=+∴=--∴=-=211111111()322113[()]22n n n n n n a a a a +++++++--- =211111()62131()222n n n n a a ++++-+-+=111111[3()]6211[3()]22n n n n a a ++++----=13{}n b 所以是等比数列。

格致中学二○一四学年度第一学期期中考试高一年级数学试卷（共4页）一、填空题：（每小题4分，满分40分） 1．函数()f x =的定义域为．2．设集合{}012M =，，，{}2|320N x x x =-+≤，则M N =．3．不等式组(2)01x x x +>⎧⎪⎨<⎪⎩的解集为．4．（理科班与平行班做）已知集合{}14A x =，，，{}21B x =，，其中x N ∈．共A B A =，则x =．（创新班做）已知全集U N =，集合{}14A x =，，，集合{}1B x =，，若U UA B Ü痧，则x =．5．（理科班与平行班做）已知函数()f x 为奇函数，且当0x <时，21()f x x x=-，则(1)f =．（创新班做）已知函数()f x 是定义在R 上的奇函数，3()()2g x f x ax =++，若(2)6g =，则(2)g -=．6．平面直角坐标系中，若点3111a a a +⎛⎫- ⎪-⎝⎭，在第三象限内，则实数a 的取值范围是．7．（理科班与平行班做）已知集合{}2|60M x x x =+-=，{}|20N y ay a =+=∈R ，，若满足MN N =的所有实数a 形成集合为A ，则A 的子集有个；（创新班做）定义b a -为区间()a b ，()a b a b ∈<R ，，的长度．则不等式234124x x x ->+的所有解集区间的长度和为；8．若不等式20x ax b ++<的解集为(31)--，，则不等式210bx ax ++≤的解集为． 9．（理科班与平行班做）若a 、b 为正实数，且3a b ab ++=，则ab 的最小值为． （创新班做）已知正数x 、y 满足：20x y xy +==，则2x y +的最小值为；10．若集合{}{}1234a b c d =，，，，，，，且下列四个关系：⑴1a ≡；⑵1b ≡/；⑶3c ≡；⑷4d ≡/有且只有一个是正确的，则符合条件的有序数组()a b c d ，，，的个数是． 二、选择题：（每小题4分，满分16分）11．若集合1131010A xx x ⎧⎫=<<∈⎨⎬⎩⎭N ，，集合{}5B x x x =∈Z ，≤，则集合A B 中的元素个数为 （） A ．11B ．13C ．15D ．1712．设函数()f x 与()g x 分别是定义在R 上的奇函数与偶函数，函数()f x 的零点个数为F ，()g x 的零点个数为G ，且F 、G 都是常数．则下列判断正确的是（）A ．F 一定是奇数，G 可能是奇数；B ．F 可能是偶数，G 一定是偶数；C ．F 一定是奇数，G 一定是偶数；D ．F 可能是偶数，G 可能是奇数．13．（理科班与平行班做）设全集为U ，对于集合A ，B ，则“A B ≡∅”是“存在集合C ，使得A C Ü且U B C Üð且U B C Üð”的（） A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分又不必要条件（创新班做）已知函数()f x 定义域为D ，区间()m n D ⊆，，对于任意的1x ，2()x m n ∈，且12x x ≠，则“()f x 是()m n ，上的增函数”是“1212()()0f x f x x x ->-”的（）A ．充分不必要条件B ．充分必要条件C ．必要不充分条件D ．既不充分又不必要条件14．给出下列说法：⑴命题“若a 、b 都是奇数，则a b +是偶数”的否命题是“若a 、b 都不是奇数，则a b +不是偶数”；⑵命题“如果A B A =，那么A B B =”是真命题； ⑶ “1x ≠或2y ≠”是“3x y +≠”的必要不充分条件． 那么其中正确的说法有（） A ．0个B ．1个C ．2个D ．3个三、解答题：（共5大题，满分44分）15．（本题满分6分）已知集合{}2A x x a =-<，集合2121x B xx ⎧-⎫=⎨⎬+⎩⎭≤，且A B ⊆，求实数a 的取值范围．16．（本题满分8分，第⑴题3分，第⑵题5分）一次函数()f x 是R 上的增函数，()()()g x f x x m =+，已知[]()165f f x x =+． ⑴求()f x ；⑵当[]13x ∈，时，()g x 有最大值13，求实数m 的值． 17．（本题满分10分，第⑴题6分，第⑵题4分）设函数()211f x x x =-+-，2()1681g x x x =-+．记()1f x ≤的解集为M ，()4g x ≤的解集为N ．⑴求MN ；⑵当x MN ∈时，求证：221`()()4x f x x f x ⎡⎤+⎣⎦≤．18．（本题满分10分，第⑴题4分，第⑵题6分）已知函数2()22(1)()f x x ax a a =--+∈R ．⑴求证：函数()f x 的图象与x 轴恒有两个不同的交点A 、B ，并求此两交点之间距离的最小值；⑵若()30f x +≥在区间(1)-+∞，上恒成立，求实数a 的取值范围． 19．（本题满分10分，第⑴题5分，第⑵题5分）⑴求证：当且仅当1m =-时，函数()f x 的奇函数； ⑵若()f x 在(1)+∞，上是增函数，求实数m 的取值范围．。

2024届上海市格致初级中学高一数学第二学期期末检测试题注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共10小题，每小题5分，共50分。

在每个小题给出的四个选项中，恰有一项是符合题目要求的1．已知直线330mx y m ++-=与直线(2)20x m y +++=平行，则实数m 的值为（ ） A ．3B ．1C ．-3或1D ．-1或32．如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示成x 的函数()f x ，则()y f x =在[0,]π上的图象大致为（ ）A ．B ．C ．D ．3．已知圆锥的侧面展开图是一个半径为6，圆心角为3π的扇形，则圆锥的高为（ ）A ．33B ．34C ．35D ．54．某几何体的三视图如图所示，则该几何体的体积为（）A ．4643π+B ．8643π+C ．16643π+D ．648π+5．《莱因德纸草书》是世界上最古老的数学著作之一，书中有一道这样的题目：把100个面包分给五个人，使每个人所得成等差数列，最大的三份之和的17是最小的两份之和，则最小的一份的量是 ( ) A ．116B ．103C ．56D ．536．在计算机BASIC 语言中，函数mod(),a b 表示整数a 被整数b 除所得的余数，如mod 6,(4)2=.用下面的程序框图，如果输入的1365a =，147b =，那么输出的结果是（ ）A ．7B ．21C ．35D ．497．设*n N ∈，则“数列{}n a 为等比数列”是“数列{}n a 满足312n n n n a a a a +++⋅=⋅”的（ ）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分也非必要条件8．边长为4的正三角形ABC 中，点D 在边AB 上，12AD DB =，M 是BC 的中点，则AM CD ⋅=（ ） A ．16B ．123C ．3-D ．8-9．设等比数列{}n a 的前n 项和为n S ，若11a =，公比2q =，则4S 的值为（ ） A ．15B ．16C ．30D ．3110．已知变量x 和y 满足关系0.11y x =-+，变量y 与z 正相关． 下列结论中正确的是（ ）A ．x 与y 负相关，x 与z 负相关B ．x 与y 正相关，x 与z 正相关C ．x 与y 正相关，x 与z 负相关D ．x 与y 负相关，x 与z 正相关二、填空题：本大题共6小题，每小题5分，共30分。

福州格致中学2014-2015学年第二学段高一数学质量检测一、选择题（本大题共20小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.若直线经过原点和点()0,1A ，则直线的倾斜角是（ ） A.30︒B. 45︒C.60︒D.90︒2.一个球的表面积是16π，那么这个球的体积是（ ） A.163π B.323π C.16πD.24π3.若直线0ax y a ++=与直线10x ay ++=平行，则a 的值为（ ） A.1B. 1±C.1-D.以上均不对4.点()1,3,2A -在x 轴的摄影和在平面xOy 的摄影分别是（ ）A.()()1,0,2,1,3,0-B. ()()1,3,2,1,3,0--C.()()1,0,0,1,0,0D.()()1,0,0,1,3,0-5.一个几何体的三视图如图，则该几何体的体积为（ ） A.2B.43C.4D.56.已知圆C 与圆()()22121x y ++-=关于点()1,0中心对称，则圆C 的方程为（ ） A.22(3)(2)1x y ++-=B. 22(3)(2)1x y -+-=C.22(2)1x y ++=D.22(2)1x y +-=7.设m ，n 是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题： ①m ⊥α，n ∥α，则m ⊥n ②若α∥β，β∥γ，m ⊥α则m ⊥γ ③若m ∥α，n ∥α则m ∥n ④若α⊥γ，β⊥γ，则α∥β A. ①和② B. ②和③ C.③和④D.①和④8.直线1y ax a=-的图像可能是（ ）A. B. C. D.9.已知四面体P ABC -各面均为正三角形，求异面直线PA 和BC 所成的角的大小（ ） A.30︒B. 45︒C.60︒D.90︒10.由直线20x y -+=上的点向圆22(4)(2)1x y -++=引切线，则切线长的最小值为（ ） A.30B.31 C.42D.33二、填空题：（本大题共4小题，每小题4分，共16分.）11.如图，一个水平放置的三角形的斜二测的直观图是等腰直角三角形，若，则原三角形的ABO 的周长是12.已知圆22(3)13y +-=（x-2）与圆22(3)9x y -+=交于AB 两点，则弦AB 的垂直平分线方程为13.半径为6的圆与x 轴相切，且与22(3)1x y +-=内切，则此圆的方程为14.矩形ABCD 的两边AB=3，AD=4，PA ⊥平面ABCD ，且PA=435，则二面角A-BD-P的度数是三、解答题（本大题共3小题，共34分，解答应写出文字说明、证明过程或演算步骤） 15.（本题10分）已知在平面直角坐标系中，三角形ABC 的三个顶点A （0，-3），B （-4,0），C （-1,4）求：（1）AC 边上的中线所在的直线方程；（2）三角形ABC 的面积16. （本题12分）已知关于x,y 的方程C ：22240x y x y m +--+=.(1)若方程C 表示圆，求m 的取值范围； （2）若圆C 与圆22812360x y x y +--+=有三条公切线，求m 的值；（3）当m=-4时，圆C 与过点（-1，-1）的直线l 相交于M ，N 两点，且25MN =，求直线l 的方程.17. （本题12分）如图，在三棱柱ABC-111A B C 中，侧棱垂直于底面，AB ⊥BC ，12AA AC ==，BC=1，E ，F 分别是11AC ，BC 的中点.（1）求证：平面ABE ⊥平面11B BCC ； （2）求证：1C F ∥平面ABE ；（3）求三棱锥E-ABC 的体积.四．选择题：（共3小题，每题5分，共15分）18.过点A （1,4）且横纵截距的绝对值相等的直线有（ ）A.1条 B 、2条 C 、3条 D 、4条19.设有平面γβα，，两两互相垂直，且三个平面有一个公共点A ，现有一个半径为1的小球与这三个平面都相切，则小球上的任一点到点A 的最近的距离是（ ） 21.A 22.B 12.-C 13.-D 20.函数2422-+=x x y 的单调递减区间为（ ）(]6,,-∞-A [)∞+-，6.B C. (]1,-∞- D.[)∞+-，1五、填空题：（共3小题，每题4分，共12分）21. 一容器盛有水，，且侧棱121=AA ，若侧面B B AA 11水平放置时，水面恰好过1111,,C B C A BC AC ，的中点，当底面ABC 水平放置时，水面高为22. 曲线241x y -+=与直线()42+-=x k y 有两个交点时，实数k 的取值范围是 23. 若函数())1,0(11≠++=a a a mx f x是奇函数，则m 的值是 六、解答题（本大题共2小题，共23分）24.在圆锥PO 中，已知2=PO ，O Θ的直径AB=2，点C 在弧AB 上，且30=∠CAB ，D 为AC 的中点（1）证明：AC ⊥平面POD（2）求直线OC 和平面PAC 所成角的正弦值25. 圆C 的半径为3，圆心C 在直线2x+y=0上且在x 轴下方，x 轴被圆C 截得的弦长为52 （1)求圆C 的方程；（2)点P 是圆上任一点，过点P 引x 轴的垂线，垂直为P ’，求PP ’的中点Q 的轨迹方程 （3)设A （0,-5），M,N 分别是直线x-y-8=0和圆C 上的动点，求MN MA +的最小值以及此时M 点坐标福州格致中学2014-2015学年第二学段高一数学质量检测参考答案一．选择题（每小题5分，共50分） 1 2 3 4 5 6 7 8 9 10 DBDDCBABDB二．填空题（每小题4分，共16）11. 22+4 12. 3x+y-9=0 13. 22x +y-=36±（4）（6） 14. o30 三．解答题（共34分）15.解：(1)AC 的中点M （-0.5，o.5）由A ，M 点得到：030.500.53x y -+=--+，化简得：-7x=y+3,即7x+y+3=0(2) 5AB =, :34120AB l x y ++=,且C 点到直线AB 的距离为2231612534d -++==+，则其面积15512.52S =⨯⨯= 16.解：（1）由1+4-m>0得m<5 (2)显然两圆外切，由此得到22(14)(26)45d m =-+-=+-，解得m=4（3）当m=-4时，圆C ：22(1)(2)9x y -+-=，r=3，则圆心（1,2）到直线l 的距离为2。

福建省福州格致中学2023-2024学年高一下学期7月期末考试数学试题一、单选题1．集合2{|2}A x x x ==，}2{1B =，，则A B ⋃=（ ） A ．{}0,1,2 B ．{}0,1 C ．{}2 D ．{}1,22．已知复数z 满足()123z i i -=-，则复数z 的虚部为（ ） A ．i -B ．iC ．1-D ．13．复数z 满足()43i i 2i z ++=-，则z =（ ）A B C D ．4．在空间中，若直线l 平行于平面α，则下列结论成立的是（ ） A ．α内不存在与l 共面的直线 B ．α内不存在与l 异面的直线 C ．α内不存在与l 垂直的直线D ．α内不存在与l 相交的直线5．如图，网格小正方形的边长为1，网格纸上绘制了一个多面体的三视图，则该多面体的体积为 （ ）A ．14B ．7C ．143 D ．736．下列函数既是偶函数，又在()0,∞+上单调递减的是（ ） A ．42y x x =+ B ．e -=x y C ．e e x x y -=-D ．ln y x =7．已知1O 是正方体1111ABCD A B C D -的中心O 关于平面1111D C B A 的对称点，则下列说法中错误的是（ ）A ．11O C 与1D C 是异面直线B ．11//OC 平面11A BCD C ．11O C BD ⊥D ．11O C ⊥平面11BDD B8．设()f x 是定义在(,0)(0,)-∞+∞U 上的奇函数，对任意的1212,(0,),x x x x ∈+∞≠，满足：()()2211210x f x x f x x x ->-，且(2)4f =，则不等式8()0f x x ->的解集为（ ）A ．(2,0)(2,)-+∞UB ．(2,0)(0,2)-UC ．(,4)(0,4)-∞-⋃D ．(,2)(2,)-∞-+∞U二、多选题9．下列运算法则正确的是（ ） A ．322log log 3a ab b =B ．()mn m n a a = C ．ln log ln a bb a=（0,0b a >>且1a ≠） D ．()0,,m nm n aa a a m n N ++=⋅≠∈10．为了普及环保知识，增强环保意识，某学校分别从两个班各抽取7位同学分成甲、乙两组参加环保知识测试，得分（十分组）如图所示，则下列描述正确的有（ ）A ．甲、乙两组成绩的平均分相等B ．甲、乙两组成绩的中位数相等C ．甲、乙两组成绩的极差相等D ．甲组成绩的方差小于乙组成绩的方差11．如图，点M 是正方体1111ABCD A B C D -中的线段1A D 上的一个动点，则下列结论正确的是（）A ．存在点M ，使//CM 平面11A BCB ．点M 存在无数个位置满足1CM AD ⊥C ．若正方体的棱长为1，三棱锥1B C MD -的体积最大值13D ．存在点M ，使异面直线1C M 与AB 所成的角是30o12．在四面体ABCD 中，AB AC ⊥，AC CD ⊥，直线AB ，CD 所成的角为60°，AB CD ==4AC =，则四面体ABCD 的外接球表面积为（ ）A B ．52π C ．80π D ．208π三、填空题13．已知集合{}{}{}1,2,3,2,,4,2,3A B m A B ==⋂=，则m =14．已知角θ的顶点与坐标原点重合，始边与x 轴的非负半轴重合，终边在直线3y x =上，则cos 2θ=.15．函数()2,048,cos x x af x x ax x a π<<⎧=⎨-+≥⎩，当1a =时，()f x 的零点个数为；若()f x 恰有4个零点，则a 的取值范围是.四、解答题16．已知O 为坐标原点，对于函数()sin cos f x a x b x =+，称向量(,)OM a b =u u u u r为函数()f x 的伴随向量，同时称函数()f x 为向量OM u u u u r的伴随函数．（1）设函数()sin()2cos 22g x x x ππ⎛⎫=++ ⎪⎝⎭-，试求()g x 的伴随向量OM u u u u r 的模；（2）记(1ON =uuu r 的伴随函数为()h x ，求使得关于x 的方程()0h x t -=在[0,]2π内恒有两个不相等实数解的实数的取值范围．17．去年我校有30名学生参加某大学的自主招生面试，面试分数与学生序号之间的统计图如下：（1）下表是根据统计图中的数据得到的频率分布表，求出a，b的值，并估计这些学生面试分数的平均值(同一组中的数据用该组区间的中点值作代表)；（2）该大学的招生办从25～30号这6位学生中随机选择两人进行访谈，求选择的两人的面试分数均在200分以上的概率．18．如图4，四边形ABCD为正方形，PD⊥平面ABCD，30⊥于点F，∠=o，AF PCDPCFE CD，交PD于点E.//（1）证明：CF⊥平面ADF；--的余弦值.（2）求二面角D AF E19．某建筑公司用8000万元购得一块空地，计划在该地块上建造一栋至少12层、每层4000平方米的楼房．经初步估计得知，如果将楼房建为x（x12）层，则每平方米的平均建筑费用为Q(x)=3000+50x（单位：元）.为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？每平方米的平均综合费最小值是多少？（注：平均综合费用=平均建筑费用+平均购地费用，平均购地费用=）20．如图，四棱锥P ﹣ABCD 中，PA ⊥底面ABCD ，，BC=CD=2，．（1）求证：BD ⊥平面PAC ；（2）若侧棱PC 上的点F 满足PF=7FC ，求三棱锥P ﹣BDF 的体积．21．已知定义在R 上的函数*()||||,f x x m x m N =--∈，且()2f x <恒成立 （1）求实数m 的值;（2）若(0,1),(0,1)αβ∈∈，且()()1f f αβ+=，求证：4118αβ+≥。