第11章 轴
- 格式:pdf
- 大小:778.60 KB
- 文档页数:18






沪科版八上数学复习要点
第十一章平面直角坐标系小结
一、平面内点的坐标特征
1、各象限内点P(a ,b)的坐标特征:
第一象限:a>0,b>0;第二象限:a<0,b>0;第三象限:a<0,b<0;第四象限:a>0,b<0
(说明:一、三象限,横、纵坐标符号相同,即ab>0;二、四象限,横、纵坐标符号相反即ab<0。
)
2、坐标轴上点P(a ,b)的坐标特征:
x轴上:a为任意实数,b=0;y轴上:b为任意实数,a=0;坐标原点:a=0,b=0
(说明:若P(a ,b)在坐标轴上,则ab=0;反之,若ab=0,则P(a ,b)在坐标轴上。
)
3、两坐标轴夹角平分线上点P(a ,b)的坐标特征:
一、三象限:a=b;二、四象限:a=-b
二、对称点的坐标特征
点P(a ,b)关于x轴的对称点是(a ,-b);
关于y轴的对称点是(-a ,b);
关于原点的对称点是(-a ,-b)
三、点到坐标轴的距离
点P(x ,y)到x轴距离为∣y∣,到y轴的距离为∣x∣
四、(1)横坐标相同的两点所在直线垂直于x轴,平行于y轴;
(2)纵坐标相同的两点所在直线垂直于y轴,平行于x轴。
五、点的平移坐标变化规律
坐标平面内,点P(x ,y)向右(或左)平移a个单位后的对应点为(x+a,y)或(x-a,y);点P(x ,y)向上(或下)平移b个单位后的对应点为(x,y+b)或(x,y-b)。
(说明:左右平移,横变纵不变,向右平移,横坐标增加,向左平移,横坐标减小;上下平移,纵变横不变,向上平移,纵坐标增加,向下平移,纵坐标减小。
简记为“右加左减,上加下减”)。


思考题及练习题12-1说明下列型号轴承的类型、尺寸系列、结构特点、公差等级及其适用场合。
62203, 6406/P2,N209/P4, 7312AC/P6, 33221B/P5。
12-2滚动轴承的寿命和基本额定寿命是什么含义?何谓基本额定动载荷?何谓当量动载荷?12-3 —深沟球轴承6304承受的径向力F r =4 kN,载荷平稳,转速n =960 r/min,室温下工作,试求该轴承的基本额定寿命,并说明达到此寿命的概率。
若载荷改为乙=2 kN,轴承的基本额定寿命是多少?12-4试求N207圆柱滚子轴承允许的最大径向载荷。
已知工作转速〃=200r/min、预期使用寿命〃=10 000h、工作温度t<100°C,载荷平稳。
12-5 一水泵轴选用深沟球轴承支承。
已知轴颈d=35 mm,转速n=2 900 r/min,轴承所受径向载荷F. =2 300 N,轴向载荷玲=540 N,工作温度t<100°C,载荷平稳,要求使用寿命& =5 000 h。
试选择轴承型号。
12-6设根据工作条件决定在轴的两端反装两个角接触球轴承,如图12-9a)所示。
轴承常温下运转,所受载荷平稳。
已知两个轴承的载荷分别为月4=2 060, F r2=l 000,外加轴向力F A =880N,轴的转速n=3 000 r/min,轴颈d=35 mm,要求轴承预期使用寿命〃=3 000 h,试选用70000AC型轴承。
12-7根据工作条件,决定在某传动轴上安装一对角接触球轴承,如图所示。
已知两个轴承的载荷分别为入1=1 470 N, F r2 =2 650 N,外加轴向力R=1 000 N,轴颈d=50 mm,转速n=5 000 r/min,常温下运转,有中等冲击,预期寿命以=2 000 h,试选择轴承型号。
12-8 一轴由一对30206轴承支承(见图12-16a),已知左、右两个轴承的载荷分别为尸皿=1600 N, 耳2=1530 N,锥齿轮所受的轴向力F A =865N,轴的转速n=384 r/min,轴承常温下运转,所受载荷平稳。


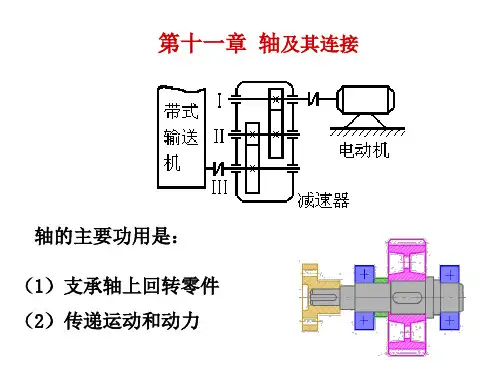
第十一章轴测图上一章所讲述的组合体的视图,是物体在相互垂直的两个或三个投影面上的多面正投影。
多面正投影图是工程上应用得最广的图样,它能够准确地表达出物体的形状和大小,但是这种图缺乏立体感,通常需要对照几个视图和运用正投影原理进行阅读,才能想象出物体的形状。
如图11-1所示,轴测图是将物体连同其参考直角坐标系,沿不平行于任一坐标面的方向,用平行投影法将其投射在单一投影面上所得到的图形。
它能同时反映出物体长、宽、高三个方向的尺度,有较强的立体感,易于识图。
但轴测图度量性较差,作图较繁,因而在工程上仅用来作为辅助图样,常用来说明产品的结构和使用,在设计和测绘中,可帮助进行空间构思、想象物体空间形状。
图11-1 轴测图的概念¤ 11-1 轴测图的基本知识一、轴测图的形成图11-1所示物体,它的正面投影只能反映长和高,水平投影只能反映长和宽,都缺乏立体感。
若在适当地位设置一个投影面P,并选取合适的投射方向S,在P面上作出物体及其参考直角坐标系的平行投影,就得到了一个能同时反映物体长、宽、高三个尺度的富有立体感的轴测图。
P平面称为轴测投影面。
162二、轴向伸缩系数和轴间角仍如图11-1所示,空间直角坐标系OX 、OY 、OZ 轴在轴测投影面上的投影O 1X 1、O 1Y 1、O 1Z 1称为轴测轴,分别简称为X 1轴、Y 1轴、Z 1轴。
当空间有直角坐标轴上的线段(或物体上与各直角坐标轴平行的线段)与轴测投影面平行时,它们在轴测投影面上的投影长度不变。
如果处于倾斜,它们的投影长度与原来的线段长度比较变短了,其长度变化的比称为轴向伸缩系数,我们用p 、q 、r 分别表示X 1、Y 1、Z 1轴的轴向伸缩系数。
从图中可以看出:οOCC O OB B O OA AO 111111r ,q , p === p 、q 、r 是变化的,它的变化是由坐标轴OX 、OY 、OZ ,投影面P ,投射方向S 相对位置不同决定的,它的变化将直接影响物体轴测图形状和大小的变化。
人教版八年级上册数学第11章 三角形 压轴题1、如图1,在ADC ∆中,4AD CD ==,30DAC ∠=︒,将ADC ∆沿直线AC 对折得ABC ∆,点E 为AB 边上一动点(与点A ,B 不重合),连接CE ,将射线CE 绕点C 顺时针旋转120︒,交射线AD 于点F . (1)求AC 的长度;(2)如图2,当E 为AB 中点时,求CF 的长度;(3)用等式表示线段AE ,AF 与AC 之间的数量关系,并加以证明.2、如图,Rt ABC ∆中,CA CB =,90ACB ∠=︒,D 为射线AC 上一点,过点D 作DE AB ⊥于点E ,F 是BD 的中点.(1)如图1,FE 与FC 有何关系,并说明理由;(2)如图2,将ADE ∆绕点A 顺时针旋转,使点D 落在ABC ∆内部,判断(1)中的结论是否还成立?如果不成立,请说明理由,如果成立,请证明;(3)将ADE ∆绕点A 顺时针旋转75︒,若2CA =,且CB BD ⊥,连接CE ,请直接写出CEF ∆的面积. 3、在OAB ∆,OCD ∆中,OA OB =,OC OD =,90AOB COD ∠=∠=︒.(1)若O 、C 、A 在一条直线上,连AD 、BC ,分别取AD 、BC 的中点M 、N 如图(1),求出线段MN 、AC 之间的数量关系;(2)若将OCD ∆绕O 旋转到如图(2)的位置,连AD 、BC ,取BC 的中点M ,请探究线段OM 、AD 之间的关系,并证明你的结论;(3)若将OCD ∆由图(1)的位置绕O 顺时针旋转角度(0360)αα︒<<︒,且4OA =,2OC =,是否存在角度α使得OC BC ⊥?若存在,请直接写出此时ABC ∆的面积;若不存在,请说明理由.4、在ABC ∆,90ACB ∠=︒,30ABC ∠=︒,将ABC ∆绕顶点C 顺时针旋转,旋转角为(0180)θθ︒<<︒,得到△A B C ''.(1)求当角θ为多少度时,△CB D '是等腰三角形;(2)如图②,连接AA ',BB ',设ACA ∆',BCB ∆'的面积分别为1S ,2S ,求12S S 的值; (3)如图③,设AC 的中点为E ,A B ''的中点为P ,AC a =,连接EP ,当旋转角θ为多少时,EP 长度最大,并求出EP 的最大值.5、已知Rt ABC ∆中,将90ACB ∠=︒,6BC =,30A ∠=︒,将ABC ∆绕点C 逆时针旋转α,(060)α︒<︒,得到DEC ∆,设直线DE 与直线AB 相交于点P (1)如图1,连接PC ,求证:PC 平分EPA ∠.(2)如图2,在ABC ∆旋转过程中,连接BE ,当BCE ∆的面积为α的度数.(3)如图3,当点P 在边AB 上时,问:PE PB +是否为定值?如果是,请求出此定值;如果不是,请说明理由.6、如图1,两块直角三角纸板(Rt ABC ∆和Rt BDE)∆按如图所示的方式摆放(重合点为)B ,其中90BDE ACB ∠=∠=︒,30ABC ∠=︒,2BD DE AC ===.将BDE ∆绕着点B 顺时针旋转.(1)当点D 在BC 上时,求CD 的长;(2)当BDE ∆旋转到A ,D ,E 三点共线时,画出相应的草图并求CDE ∆的面积(3)如图2,连接CD ,点G 是CD 的中点,连接AG ,求AG 的最大值和最小值.7、(1)如图1,点P 是等边ABC ∆内一点,已知3PA =,4PB =,5PC =,求APB ∠的度数.分析:要直接求A ∠的度数显然很因难,注意到条件中的三边长恰好是一组勾股数,因此考虑借助旋转把这三边集中到一个三角形内.解:如图2,作60PAD ∠=︒使AD AP =,连接PD ,CD ,则PAD ∆是等边三角形.∴ 3AD AP ===,60ADP PAD ∠=∠=︒ABC ∆是等边三角形AC AB ∴=,60BAC BAP ∠=︒∴∠= ABP ACD ∴∆≅∆4BP CD ∴==, ADC =∠在PCD ∆中,3PD =,5PC =,4CD =,222PD CD PC += PDC ∴∠= ︒6090150APB ADC ADP PDC ∴∠=∠=∠+∠=︒+︒=︒(2)如图3,在ABC ∆中,AB BC =,90ABC ∠=︒,点P 是ABC ∆内一点,1PA =,2PB =,3PC =,求APB ∠的度数.8. 拓展应用.如图(4),ABC ∆中,30ABC ∠=︒,4AB =,5BC =,P 是ABC ∆内部的任意一点,连接PA ,PB ,PC ,则PA PB PC ++的最小值为 .9、如图,ABC ∆中,1AB AC ==,45BAC ∠=︒,AEF ∆是由ABC ∆绕点A 按顺时针方向旋转得到的,连接BE 、CF 相交于点D .(1)求证:BE CF =;(2)当四边形ACDE 为菱形时,求BE 的长.10、如图1,在Rt△ABC中,∠ACB=Rt∠,AB=10,AC=6,点D以每秒5个单位长度的速度从点B处沿沿射线BC方向运动,点F以相同的速度从点A出发沿边AB向点B运动,当F运动至点B时,点D、E同时停止运动,设点D运动时间为t秒.(1)用含t的代数式分别表示线段BD和BF的长度.则BD=,BF=.(2)设△BDF的面积为S,求S关于t的函数表达式及S的最大值.(3)如图2,以DF为对角线作正方形DEFG.在运动过程中,是否存在正方形DEFG的一边恰好落在Rt△ABC 的一边上,若存在,求出所有符合条件的t值;若不存在,请说明理由.11、如图1,以∠ACB 为顶角的等腰Rt△ABC 是由等腰Rt△EDC 中绕点C 顺时针旋转α°(0°<α°<90°),AB 交CE 于F,ED 分别交AB、BC 于M、H.(1)试判断CF 与CH 的数量关系,并说明理由;(2)(2)如图2,若∠BCE=45°,求证:四边形ACDM 是菱形。